计算机模拟薄膜生长过程研究

孙治国

摘要：该文采用Monte Carlo算法，以面心立方结构材料为例，对薄膜生长过程中的应力进行了计算机模拟，同时也模拟了在薄膜生长的过程中表面粗糙和基底温度之间所存在的关系。通过模拟结果发现，当基底温度较低时薄膜表面相对粗糙，而随着基底温度的身高表面粗糙程度则随之下降，而当温度到达一定程度时表面粗糙度会达到最低，之后这回随着温度的升高粗糙度又将升高。模拟结果还表明在一定原子入射率下，当薄膜沉积相同厚度下，薄膜应力随基底温度的增大而减小。

关键词：Monte Carlo法；薄膜生长；薄膜应力；薄膜粗糙度

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2015）25-0161-02

1 概述

Monte Carlo算法也被称为随机模型算法、随机抽样或统计实验方法。该算法主要用来模拟生长过程，其基本思想是：先确立起一个概率模型或者随机过程，然后对该模型或者过程进行观察或者是抽样实验，根据观察或者实验来对所求参数的统计特征进行计算，并最后得出所求解的近似解。

如今，对薄膜應力在薄膜的基础理论研究以及应用研究非常关注，通过研究能够更好地了解应力对于薄膜生长过程以及微观结构所能够带来的影响。通过对控制应力所形成的条件从而对应力大小进行控制，使得原件的寿命能够得到提高，并减少薄膜元件的形变。有报道显示，已经从实验中发现薄膜应力和薄膜表面粗糙度与薄膜厚度以及原子沉积时间之间存在有一定的联系 [1-2]，本文是用计算机手段来对薄膜应力进行模拟。

2 算法与模型

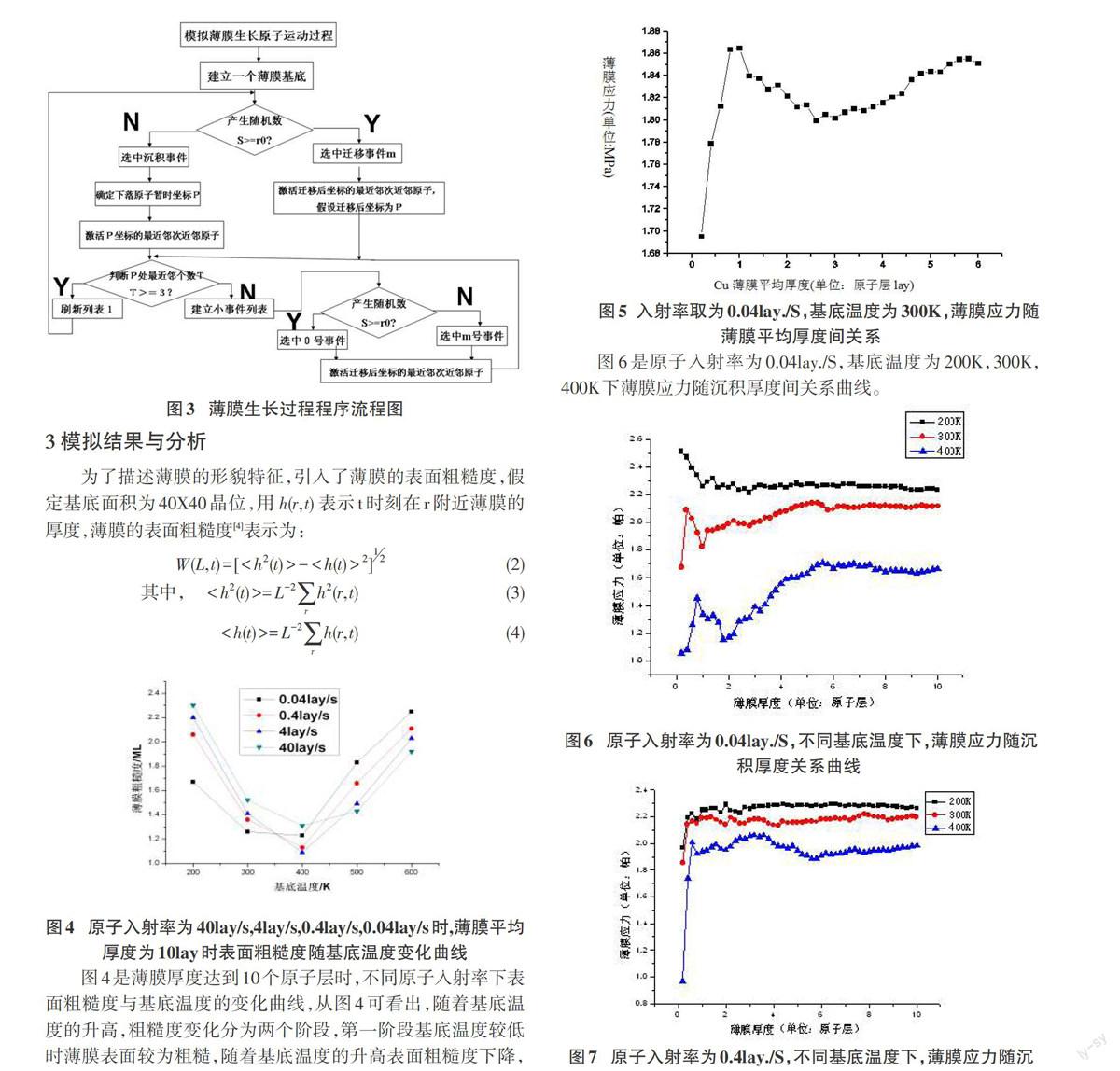
在薄膜三维生长过程中，基底采用正方形网格结构，建立三维点阵来处理原子在空间中的排列结构，具体的排列结构如图1所示。薄膜生长过程主要考虑三种动力学过程：吸附过程、迁移过程和脱附过程。吸附过程中原子以一定的沉积速率入射并被生长表面吸附；迁移过程中既考虑了原子层内迁移，又考虑了原子层间迁移过程；脱附过程是指原子在运动过程中从生长系统中脱离出来。

在薄膜三维生长过程中，原子的吸附、迁移和脱附过程都具有不同的发生概率，将所有的过程组成概率事件列表，通过Monte Carlo从列表中随机抽取一个过程执行。在这个被抽取的过程执行之后，所有的原子这将会重新排列，这个时候就对过程列表进行刷新以对新的事件发生进行确认。其中过程事件被抽取的概率等于这事件的发生概率和过程列表中的所有过程概率之和之间的比值。

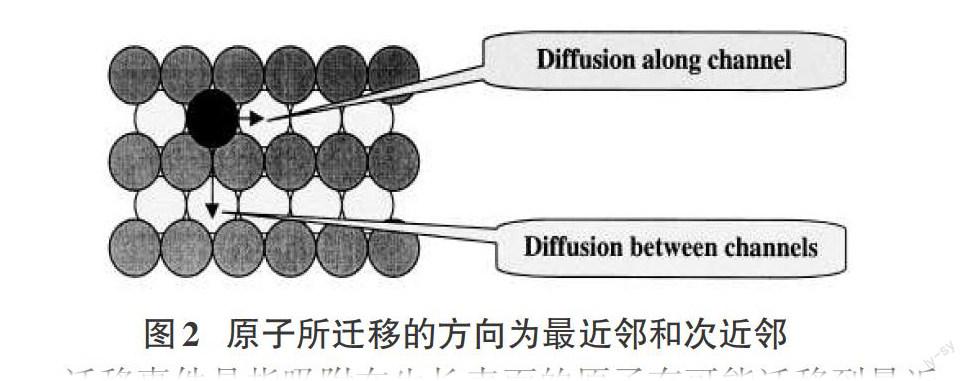
沉积事件发生的几率是指单位时间内入射到基底表面的原子数。如果发生的是原子的沉积过程，那么沉积一个原子于基底的随机位置坐标为（i，j）。若此位置满足三个最近邻，沉积原子将停留在此，否则原子将向其最近邻和次近邻处迁移[3-4]如图2，直到找到满足最少三个最近邻，完成沉积过程。

迁移事件是指吸附在生长表面的原子有可能迁移到最近邻或次近邻的空位上，其发生概率为

[r=ν0exp-ΔEkBT] （1）

其中[ν0=（2KBT）/h]，[KB]为玻尔滋蔓常数，[h]为普朗克常数，[ΔE]为原子迁移的激活能，T为基底温度。

脱附事件是指生长表面上的原子有可能因为热运动等原因而脱离生长表面，其发生概率表达式与迁移过程一致，只是目标位置不再有任何最近邻原子。

本文在模拟薄膜生长过程中所采用的技术线路如下：

3 模拟结果与分析

为了描述薄膜的形貌特征，引入了薄膜的表面粗糙度，假定基底面积为40X40晶位，用[h（r，t）]表示t时刻在r附近薄膜的厚度，薄膜的表面粗糙度[4]表示为：

s时，薄膜平均厚度为10lay时表面粗糙度随基底温度变化曲线

图4是薄膜厚度达到10个原子层时，不同原子入射率下表面粗糙度与基底温度的变化曲线，从图4可看出，随着基底温度的升高，粗糙度变化分为两个阶段，第一阶段基底温度较低时薄膜表面较为粗糙，随着基底温度的升高表面粗糙度下降，当达到某一最佳温度时表面粗糙度达到最低值，第二阶段随着基底温度的升高，粗糙度的值又将升高。这是因为温度较低时，随着基底温度升高，构成薄膜的原子扩散能力趋于增强，导致粗糙度下降，但当温度增大至原子能够从低位置向粗糙不平的高位置跳跃时，粗糙度随着基底温度的升高不断增强。

图5为在温度为300K，原子入射率为0.04lay./S，薄膜应力与薄膜厚度间关系曲线，此曲线图与Sunjungkim，Jun-Ho Tang通过电子沉积试验方法模拟的结论[4-9]基本吻合，从图线上可以看出，在沉积一个原子层薄膜厚度前薄膜应力随着薄膜的平均厚度呈现增长趋势。

Cu薄膜平均厚度（单位：原子层lay）

图7 原子入射率为0.4lay./S，不同基底温度下，薄膜应力随沉积厚度关系曲线

从图6和图7关系曲线上可以看出，在一定原子入射率下当沉积薄膜相同厚度时，薄膜应力随着基底温度的增加而呈减小趋势。

4 结论

用Monte carlo法模拟了薄膜生长过程中的原子随机过程，考虑了原子的沉积过程、扩散过程和脱附过程。合理选择了原子间的作用势能以及周期性边界条件。模拟结果表明，在基底温度较低时薄膜表面较为粗糙，随着基底温度的升高表面粗糙度下降，当达到某一最佳温度时表面粗糙度达到最低值，随着基底温度的升高，粗糙度又将升高。模拟结果还表明在一定原 子入射率下，当薄膜沉积相同厚度下，薄膜应力随基底温度的增大而减小。

参考文献：

[1] Friesen C，Seel S C，Thompson C V.Reversible stress changes at all stages of Volmer—Weber film growth[J] .Journal of Applie Physics，2003（95）：1010-1020.

[2]James B.Adams，Zhiyong Wang，Youhong Li.Modeing Cu thin film growth[J].Thin Solid Films ，2000（365）：201-210.

[3] Saka M， Yamaya F.Rapid and mass growth of stress-induced nanowhiskers on the surfaces of evaporated polycrystalline Cu films[J].Scripta Materialia ，2007（56）：1031-1034.

[4] Fujiwara K，Tanimoto H，Mizubayashi H.Elasticity study of very thin Cu films[J]. Materials Science and Engineering A，2006（442）：336-341.

[5] Kim S，Jun-Ho Jang，Jeong-Soo Lee，et al.Stress behavior of electrodeposited copper films as mechanical supporters for light emitting diodes[J].Electrochimica Acta ，2007（52）： 5285-5265.

[6] 周雪飞，吴冲.动力学蒙特卡罗模拟薄膜生长[J].人工晶体学报，2012，41（3）：792-796.

[7] 张佩峰，郑小平，贺德衍.薄膜生长过程的Monte Carlo模拟[J].中国科学（G辑），2003，33（4）：340-347.

[8]Henelius P，Frobrich P，Kuntz P J，et al.Quantum Monte Carlo simulation of thin magnetic films .Phys.RevB，2002，66：094407，1-8.

[9]郑小平，张佩峰，范德旺，等. 薄膜生长的计算机模拟[J].材料研究学报，2005，19（2）：170-178.