圆柱状食品解冻时间的数值求解和实验验证

纪志坚 李徽 于燕 牛新朝 王钊 杨宝江

（1.松下冷链（大连）有限公司 辽宁大连 116600；2.哈尔滨商业大学 黑龙江哈尔滨 150028）

圆柱状食品解冻时间的数值求解和实验验证

纪志坚1李徽1于燕1牛新朝2王钊1杨宝江1

（1.松下冷链（大连）有限公司 辽宁大连 116600；2.哈尔滨商业大学 黑龙江哈尔滨 150028）

预测冻结食品解冻过程中的温度变化和解冻时间在实际生产和生活中十分有意义。本文提出了冻结的圆柱状食品在解冻过程中的物理模型，分别用有限差分法和元体平衡法两种方法相结合对其解冻时间和中心区域、R/2处以及边界节点温度进行求解。并以牛肉为例进行了实验验证。通过数值计算和实验验证，得出了理论解冻时间与实验之间的最大误差为8.4%。结果表明：采用数值法预测解冻时间和温度变化曲线与实验结果有着较高的吻合度。同时，中心区域的温度最大误差为1.2℃，R/2处的温度最大误差为0.8℃，边界节点处温度最大误差为1.5℃，由此说明数值模拟在研究冻结食品的解冻方面是可信的。

食品解冻；解冻时间；温度曲线；数值求解；实验验证

0 引言

冷冻冷藏食品业是近年来国际上发展最快的食品行业之一，在中国的发展也极为迅速。2013年上半年我国冷冻食品进出口贸易额呈上升趋势进出口总值132.9亿美元，同比增长14.3%。与此同时，人们也一直关注有关食品的冷冻和解冻理论，因为这直接关系到食品安全与质量问题。从理论上讲，解冻是冻结的逆过程，但是，两者不但在相变方向、冷却过程和加热过程上不同，在食品的冻结时间和内部温度变化方面还有很多不同之处[1]。解冻过程是使冻结食品中的冰晶融化成水，并被食品吸收而恢复到冻结前的新鲜状态。在解冻过程中细胞的复原程度的好坏决定了解冻产品质量的高低[2]，因此解冻过程比冻结过程要复杂的多。

在解冻肉类过程中要求[3]：（1）均匀的半解冻状态最好；（2）在解冻过程中肉组织流出的汁液要尽量的少；（3）抑制微生物的繁殖和生成；（4）解冻介质温度低，不超过20℃；（5）解冻时的温度不要太高以免破坏组织结构；（6）解冻的速度尽可能快，以缩短食品在较高温度下停留的

时间。速冻蔬菜、面包、糕点等适合快速解冻而鱼肉和畜肉采用慢解冻的效果更好[4]。

本文针对圆柱状食品的解冻时间进行了研究，以半径R=32mm速冻的牛肉卷为研究对象。为了在求解过程中研究方便， 对研究对象和环境做了几个假设：牛肉的导热系数和比热仅与温度有关而与其他因素的关系忽略；牛肉的密度为常数；周围环境认为是无限大空间，因此周围介质的温度不随时间而改变；牛肉卷的解冻过程中认为是大长径比，故解冻过程中热量传递主要发生在径向上，而沿轴向上的热量传递是微弱的，因此可忽略，即导热为一维导热；温度场分布是均匀的。

从冰箱冷冻室取出牛肉卷，通过测量得到初始温度为-20℃，解冻终了温度要求中心温度达到0.5℃，在此温度前提下进行研究和实验对比。

图1 圆柱状食品传热物理模型

图2 中心节点网格划分图

图3 内部节点网格划分图

图4 边界节点网格划分图

1 研究方法

1.1 物理模型

如图1所示的圆柱形牛肉卷解冻过程中热量传递的物理模型建立圆柱状食品的非稳态导热数值模型[5]：

初始条件：τ=0 T=T0(0<=r<=R)；

1.2 数值分析

根据牛肉卷的形状可将其看成圆柱状，将初温为T=-20℃，半径R=36mm的牛肉卷放置在温度为20℃的环境中和放入12℃的水分别进行自然状态下的解冻，牛肉卷与周围空气的自然对流系数为h1，与水之间的自然对流换热系数为h2。牛肉卷外表面与周围空气之间的换热符合牛

顿冷却定律且圆柱的外表面各点的换热情况是相同的，所以圆柱状食品的温度分布沿直径方向上是对称的[6]。为了研究过程中的方便，将坐标原点放在圆心处，仅研究半径方向上的参数变化，其物理模型参见图1，采用有限差分法建立求解方程。

如图1所示，用外节点法沿半径R方向上划分n-1个内部单元和两个半单元（分别位于中心和表面边界处），图中实线为控制节点所在位置线，共有n+1个节点，Δr=R/n为空间位置步长，Δ τ为时间步长。在每一个单元内温度近似看成集中参数而不是分布函数[6]。同时为了结果的收敛性，控制方程用有限差分法差分是采用隐式格式，如此可保证计算结果无条件收敛。当中心节点的温度T<=0.5℃则迭代过程结束。

1.3 建立差分方程

图2为中心节点网络划分图。用泰勒级数展开法对中心节点0号建立节点方程：

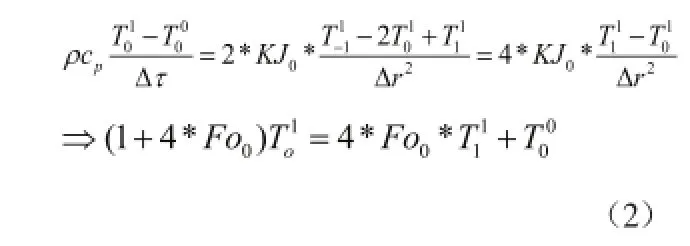
图3为内部节点网格划分图，用元体平衡法对内部节点i建立节点方程：

图4为边界节点网格划分图，用泰勒级数展开法对边界节点36号建立节点方程：

式中：

Δr——空间步长，取值为0.001m；

Δτ——时间步长，取值为20s；

KJi——i号控制体右界面上的导热系数，KJi=2KiKi+1/(Ki+Ki+1)；

Ki——i号节点的导热系数。

根据已知的冻结牛肉的导热系数，对其进行拟合得到关于导热系数与温度之间的关系方程K=-0.0001T3-0.0062T2-0.1407T+0.4848(-30<=T<=0)；当T>0时K=0.48W/(m•℃)；

ρ——牛肉的密度，取值1050kg/m³；

Cp——牛肉的比热。

根据牛肉的冰点温度-2℃来界定Cp的取值，当T<=-2时，Cp=3230J/(kg•℃)；当T>-2℃时，Cp=1720 J/(Kg•℃)；Foi为i号控制体右边界的傅里叶数，其计算公式为Foi=KJiΔτ/(ρCpΔr2)；Bi为毕渥数。

1.4 程序框图

根据TDMA法对物理模型进行程序求解，其中T[i]表示i号节点的温度，当中心节点的温度不小于0.5℃时迭代结束；M表示迭代次数，在所有节点温度进行一次迭代时M+1，具体见图5数值计算程序框图所示。

图5 数值计算程序框图

2 结果与讨论

通过实验和理论求解，现将所得的结果绘制成空气中解冻的温度随时间变化曲线和水中解冻的温度随时间变化曲线，如图8、9所示，由于篇幅限制，图中仅显示部分重要节点的温度值，如中心节点、R/2节点、边界节点处的温度逐时值。同时将空气和水中解冻时间的理论与实验值的对比在图6、7中显示。

从图8、9中曲线可知，理论与实验的结果基本吻合，但不可避免的仍有误差，通过数值计算可知理论解冻时间与实验之间空气解冻误差为7.8%、水解冻的误差为8.4%。同时，两种解冻方式对比中心区域的温度最大误差为1.2℃，R/2处的温度最大误差为0.8℃，边界节点处温度最大误差为1.5℃。分析误差产生的原因主要有：

（1）建立物理模型时忽略了辐射换热对整个过程的影响。

（2）实验仪器由于精度问题而产生的误差。

（3）被测量牛肉卷由于带有塑料薄膜外包装使表面热阻增大而减弱了换热过程，另一方面，在解冻过程中由于水分的迁移会使其物性参数发生变化，这都会使实验与理论结果产生误差。

（4）在解冻过程中周围局部环境并非稳定工况。

（5）在解冻时忽略了沿轴向的导热过程。

（6）人为操作造成的误差，如热电偶探头埋点位置的偏差。

图6 空气解冻时间实验值与数值解对比图

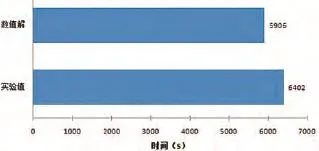
图7 水解冻时间实验值与数值解对比图

3 结论与展望

通过对解冻时间和解冻过程中温度变化的求解，对于实际生活中具有指导意义。这也使人们对于解冻过程中的变化有更深的了解，从上述的理论与实验的数据中可以得到以下结论：

（1）冻结物解冻时间和温度分布的求解，对于冷链系统中的物流过程有着重要的指导意义和现实意义。比如在环境温度已知的情况下，通过数值计算就会得到冻结食品内部温度随时间的变化情况，这将对冷藏车制冷机组何时开启起着重要的指导作用，从而使冷链中的物流过程在保证冻结物正常温度的情况下减少机组工作时间降低能耗达到节能减排的效果。

（2）通过对冻结物水解冻和空气解冻两种方式解冻时间的数值计算及实验，能够较准确的预测解冻时间，这对于餐饮行业有一定的指导意义。

（3）假如在建立模型的过程中，考虑轴向的传热和辐射换热两种情况，进一步建立起二维导热辐射模型来进行圆柱状解冻的数值计算，那么所得到的结果应该与实验结果的吻合度会更理想、可靠度更高。

图8 空气中解冻温度逐时值变化曲线

图9 水中解冻温度逐时值变化曲线

[1] 尤瑜敏. 冻结食品的解冻技术[J]. 食品科学, 2001, 22(8): 87-90.

[2] 季阿敏. 半球状食品解冻时间的数值模拟与实验研究[J]. 中国食品学报, 2006,6(3): 79-83.

[3] 冯晚平, 胡娟. 冷冻猪肉新型解冻方法对比试验研究[J]. 农产品加工. 学刊, 2011(9): 33-36.

[4] 王玉文, 张玉敏, 余善鸣. 食品冷冻理论及应用[J]. 1989.

[5] 陶文铨. 数值传热学[M]. 西安交通大学出版社, 1988.

[6] 关志强, 戴午子. 冻结食品解冻时间的数值计算[J].湛江海洋大学学报, 1999,19(4): 45-48.

Cylindrical food thawing time numerical and experimental validation

JI Zhijian1LI Hui1YU Yan1NIU Xinchao2WANG Zhao1YANG Baojiang1
（1.Panasonic Appliances Cold Chain (Dalian) Co.,Ltd. Dalian 116600; 2.Harbin University of Commerce Haerbin 150028）

It is very meaningful to predict the temperature and thawing time during the thawing process of frozen food in production and life, this paper proposes a physical model of cylindrical frozen food during the thawing process, combine the finite difference method with element balance method to solve the thawing time and the temperature at regional center R/2 and boundary nodes. Take the beef as an example for the experimental verification. Through numerical calculation and experimental verification, the maximum error between the theory thawing time and experiment is 8.4%. The results show that: it is highly consistent with the experimental results that using numerical method to predict the thawing time and temperature change curve, at the same time, the temperature maximum error in center area is 1.2℃, the temperature maximum error of R/2 is 0.8℃, the temperature maximum error of the boundary node is 1.5℃, so the numerical simulation in studying thawing of freezing food is fairly reliable.

Food thawing; Thawing time; Temperature curve; Numerical solution; Experimental verification