基于INFORM的简化IPMSM转子初始位置检测方法
王永福,王春阳
(长春理工大学 电子信息工程学院,长春 130022)
永磁同步电动机的无传感器控制,无论采取何种控制算法:矢量控制(FOC),直接转矩控制(DTC),或者基于反电势检测的标量控制,在启动时,都需要确定转子的初始位置。确定转子初始位置的方法归纳起来分为两类:第一类是预置转子位置[1,2],给电机定子绕组一个固定方向的电压矢量,强制转子转动,使转子磁场方向与该电压矢量方向重合,并规定这个确定的电压矢量方向为零矢量方向,从而标定出转子的位置。该方法的优点是控制算法实现简单可靠,在工程上已经大量的采用;缺点是在定位过程中,转子可能转动一定角度,并且转动的方向不确定,这在某些应用中是不允许的,例如汽车发动机的油泵驱动系统中,要求电机只能按照一个方向转动。第二类是基于电机凸极效应的检测。凸极效应是由电机磁路饱和或者电机本体结构不对称形成的,将电机三相绕组和逆变器看成一个整体后,便可赋予三相绕组电压以空间特性。注入绕组电压矢量激励信号,根据电流响应,计算出转子的初始位置。基于电机凸极效应的转子初始位置检测电机在d-q转子坐标系下的模型,向电机绕组中注入高频的高压信号,要求该信号频率应远高于基波频率。
计算方法大体分为两种:第一种如文献[3,4]中提出的向电机定子绕组中注入高次谐波获得转子初始位置:根据注入的高频电压信号可以是在d轴或者q轴上脉动的电压信号,也可以是一个空间旋转的高频电压信号。该方法可以准确检测出转子的初始位置,但是容易受到其他次谐波、逆变器的非线性和死区的影响[5,6],而且算法复杂,需大量的数学计算和坐标变化,对控制器件要求较高,在永磁同步电机无传感器矢量控制中应用较多;第二种如文献[7-10]中提出的定子绕组暂态电流响应的方法。利用每个电压脉宽调制(PWM)周期中,空间电压激励阶跃,引起电流的阶跃响应来计算得到转子位置,该方法无需额外的硬件电路,并且得到高SNR信号。文献[8]中提出的方法称为INFORM(indirect flux detection by on-line reactance measurement),通过在连续三个PWM周期中施加测试电压矢量得到电流变化信号,经过计算得到转子磁场在复平面上的表达式,通过反正切计算得到具体的转子位置角度。该方法的缺点是在检测周期中增加了电机电流的波动;文献[7,9,10]针对此缺点提出了改进方法。但是仍需要根据多次测量的电流变化值经过大量计算来得到电机凸极在空间复平面上的位置表达式,经过反三角运算得出具体转子位置。同高频注入法相同,对控制器件要求比较高,降低了整体系统的经济性。
本文针对内嵌式永磁同步电动机(IPMSM),基于INFORM的基本原理,提出一种简化的转子初始位置检测方法。该方法只针对静止时转子位置的检测,无需经典INFORM中的凸极位置的计算,根据测量的相电流变化值,经过简单计算,比较便可得到转子的位置。若在实际应用中配合升压升频或者I-F启动策略[11],可大大提高电机启动阶段的性能。
1 理论基础
交流感应电机(IM)、交流同步电机(PM)及交流磁阻电机(SM)统称为交流电机(AC motor)。这些类型的电机都具有相同的定子结构,不同的转子类型决定了它们的种类。但是对交流电机都有一个共同的特点:磁路特性和电机转子的位置有着密切的关系,具体表现在电机绕组感抗随转子位置周期变化。这样的特点是由电机磁场的各向差异性引起,即电机的凸极效应。AC motor的凸极效应可以由电机本体的结构引起,例如齿槽、极靴、转子几何结构的不对称等;或者是由电机磁场磁路饱和引起。由于转子几何结构的不对称引起内嵌式永磁同步电机(IPMSM)的凸极效应。图1是在Maxwell电磁仿真软件下的IPMSM电机结构和磁路分析模型。
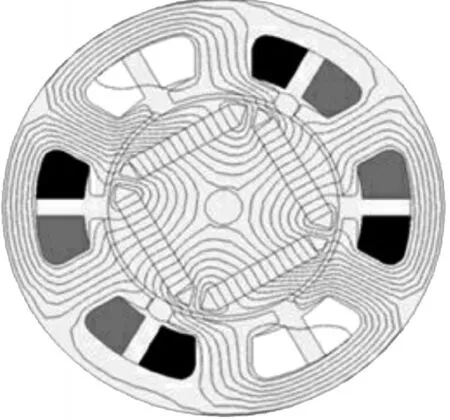
图1 结构和磁路模型

表1 电机参数
由于转子结构的不对称引起电机定子绕组三相电感量周期变化。忽略齿槽和极靴等对磁路的影响,电机定子绕组的电感量将相对转子位置按照正弦规律变化。按照表1给出的IPMSM参数,通过Maxwell仿真软件得出图2所示的电机A相电感变化图。
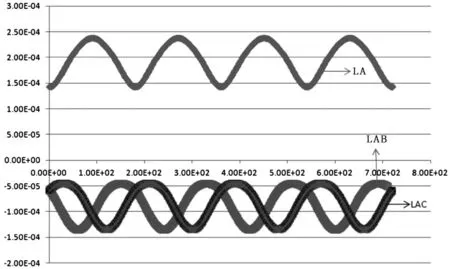
图2 电机A相电感
考虑由转子不对称引起的电机凸极效应,三相绕组Y形接法的内嵌式永磁同步电动机三相电感可用方程(1)表示[8]:
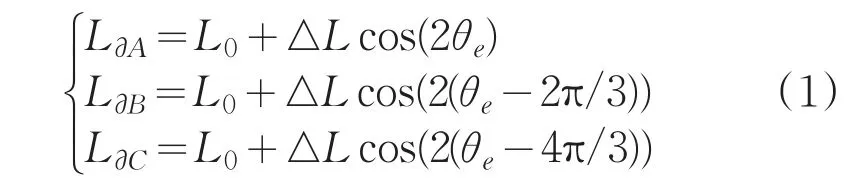
其中,L∂A,L∂B,L∂C表示绕组三相电感;L0表示绕组的平均电感量;△L表示电感的变化量;θe表示转子的电角度(主磁场的电角度)。
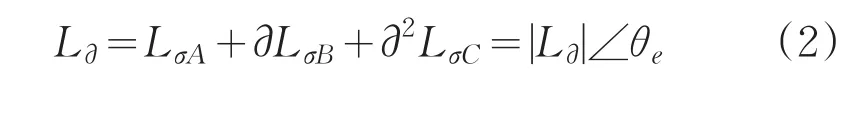
将(1)式三相绕组坐标系的电感量变换到α-β坐标系中,得复平面中的方程(2)其中,是电感的幅值,θe是复平面中的相角。在α-β坐标系中,电机绕组的电压方程为

其中,Us表示定子电压矢量;is表示定子电流矢量;rs表示定子电阻;L∂表示定子电感;e表示感应电动势矢量。
在转子静止条件下感应电动势e可以忽略;通常由于定子电阻引起的电压降同电感感应的电动势比较值非常小,所以可以忽略电阻is,得:
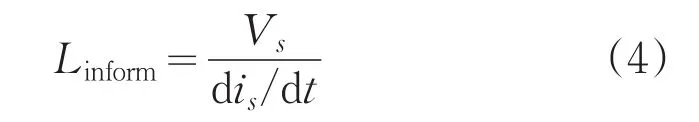
根据(4)式,在空间电压矢量 |Vs|∠θv作用下,可得到复平面的在线阻抗测量值Linform:
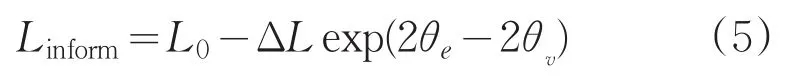
图3表示Linform随转子位置变化示意图。当转子INFORM轴分别与电压矢量方向重合时,得到最大和最小电感量:
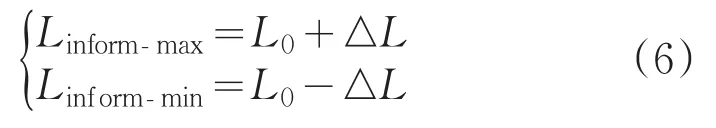
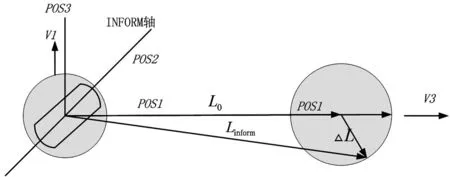
图3 Linform变化示意图
现代电机控制中,最典型的逆变电器是由三相可控半桥组成的两电平电压型逆变器。该逆变器可以提供6个有效电压矢量和2个零电压矢量,如图4所示。将电动机和逆变器看成一个整体,由这6个电压矢量和2个零矢量根据伏秒平衡原理可以合成幅值可调的任意空间位置的电压矢量,即SVPWM。在定子坐标轴系α-β中,合成空间电压矢量可以表示成方程(7):
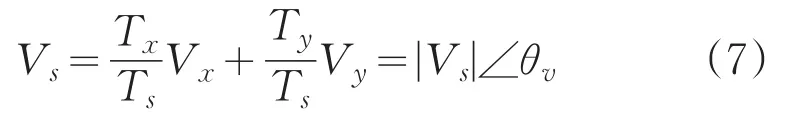
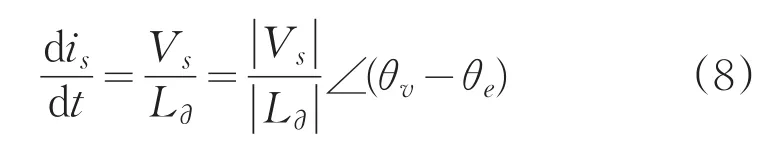
由方程(8)可以得到当θv=θe时,空间电流矢量变化值最大。根据这个原理,可以将电机绕组通入幅值相同但是相位不同的测试电压矢量,通过测量电流变化的大小来判断转子的位置。该方法不需要如参考文献[5,6,8-10]中一样,通过复杂的计算来获得转子位置。
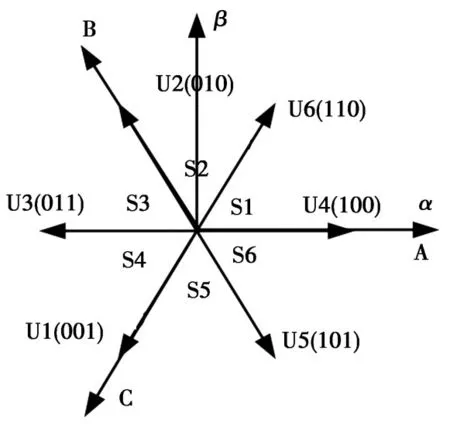
图4 基本电压矢量图
2 估算方法
建立如图5所示的电机系统坐标系。α-β坐标是两相定子固定坐标系,α轴与A相定子绕组的轴线重合;N-pole轴与转子磁场轴线重合;θre是实际转子位置;d-q坐标系是转子位置估计坐标系;θv是测试电压矢量的空间位置角度。

图5 坐标系图
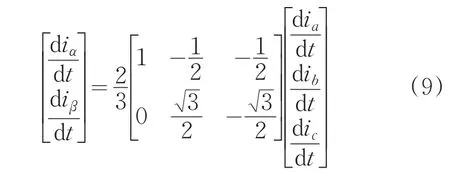
得测量电流的幅值的平方:
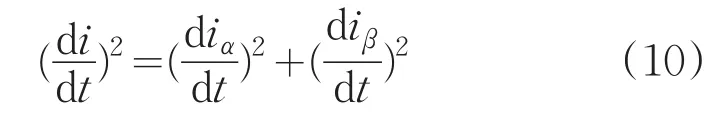
根据系统要求的要求精度选择电压测量矢量步进角△θv,对一般的控制算法,测量精度在3°~15°即可满足控制要求,即△θv=3°~15°。将每一步测量的电流平方值记录下来,选择最大电流平方值对应的角度即为转子位置。图6为电流响应的示意图。为了保证电流测量的精度,需要施加的电压矢量持续足够长的时间和具有一定的幅值大小。具体的数据需要根据具体的电机系统实验测得。
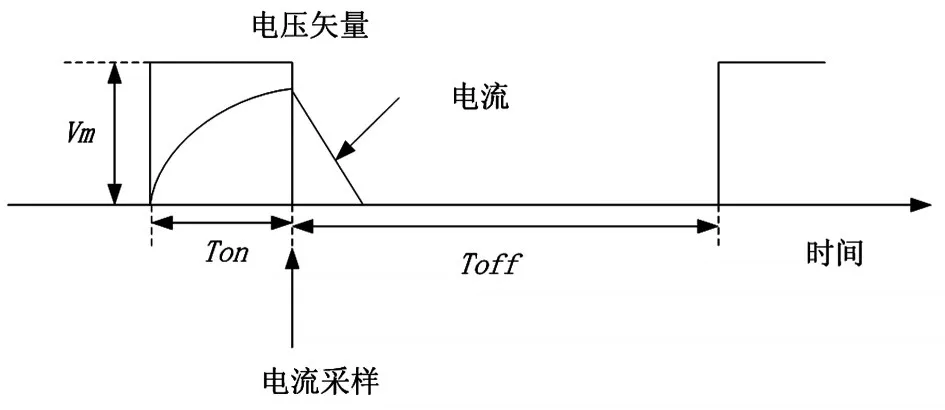
图6 电流响应示意图
3 仿真与实验
本实验的系统框图如图7所示,使用的电机参数如表1所示。对于本算法的实现,因为系统要进行一系列数学运算,因此需要控制器具有硬件的乘除法器。
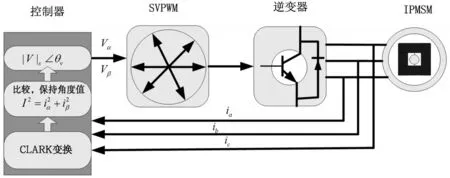
图7 系统框图
如表1所示的电机参数,绕组电感量非常小,因此在电压激励下的电流斜坡持续时间非常短,因此为了确保实验结果的准确性,至少需要10位精度的ADC,并保证ADC的采样速度在1M/s以上,同时具PWM同步触发ADC功能。首先在搭建MATLAB模型验证了转子在185°和106°时的转子位置和电流的对应波形,如图8和图9所示。
在如图12所示的实验平台上,给出测得的A相电流波形图10,从图中可以看出电流上升边沿持续的时间非常短,而且在开通的时候,由于功率器件寄生参数的影响,有高频振荡产生。因此在电流变化测量时,ADC采样和转换速度要足够快,并且在功率器件打开后需要延时一定时间采样,本实验中采样间隔取40μs,延时时间取8μs;图11为测量实际转子位置,估计转子位置和对应的电流采样。
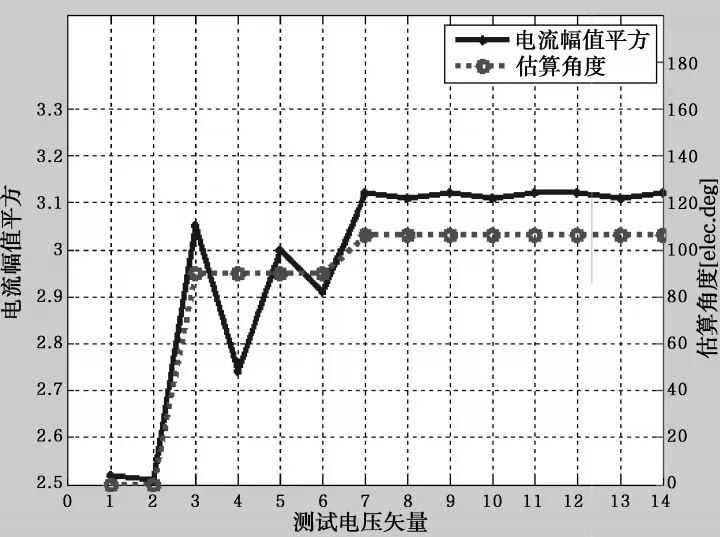
图8 角度在185°时的估计
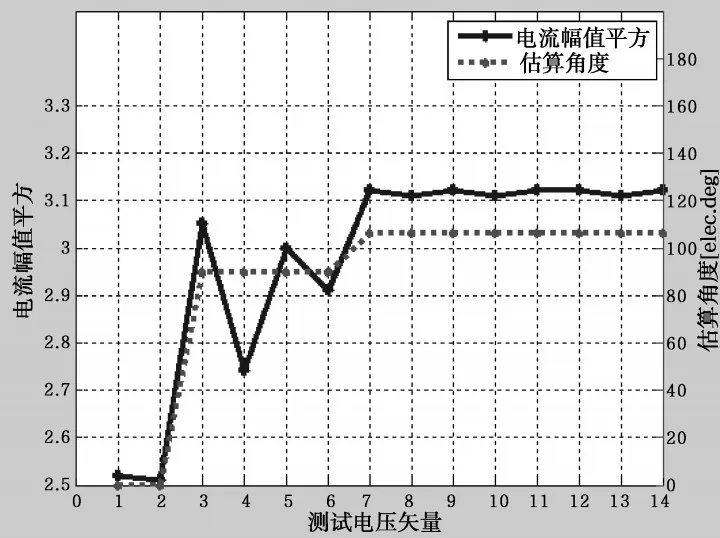
图9 角度在106°时的估计
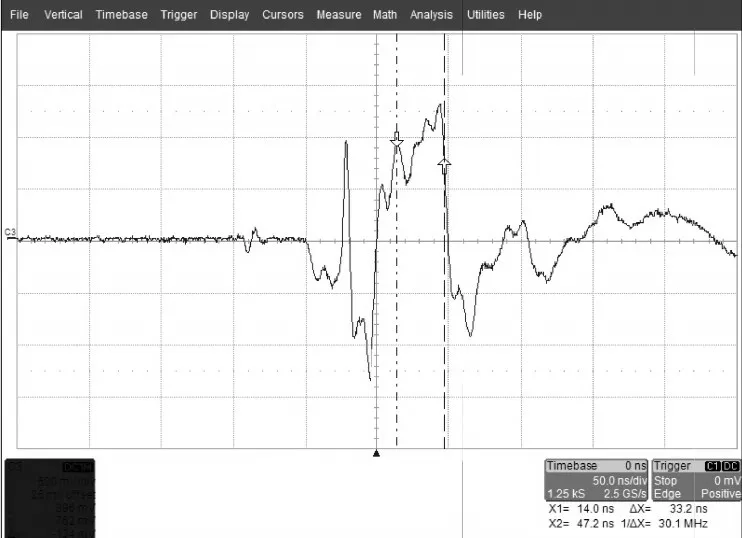
图10 A相电流
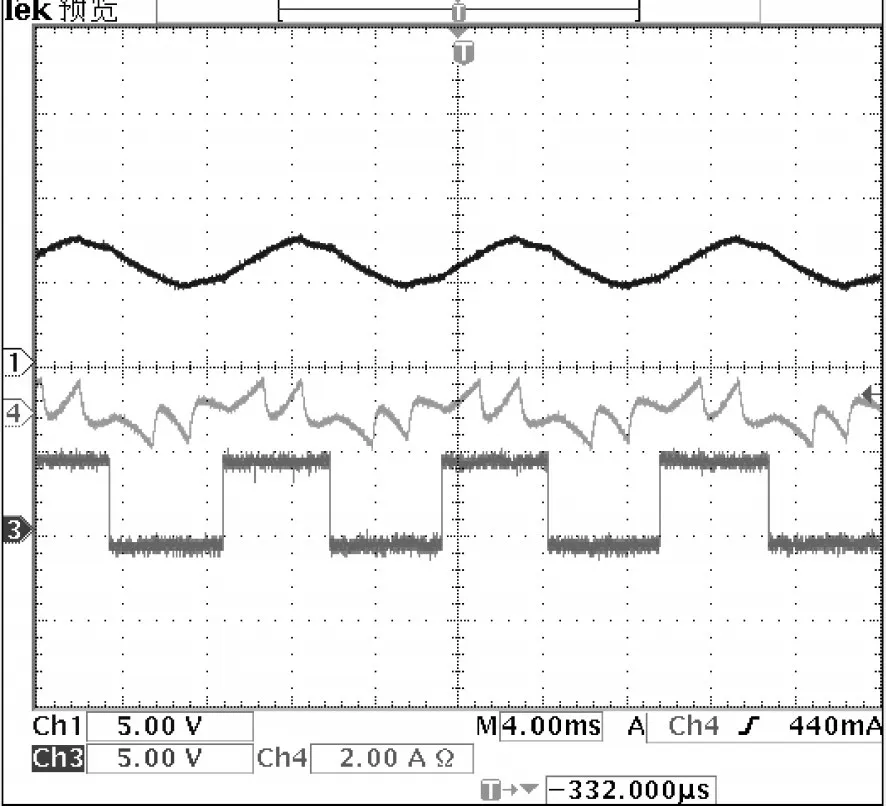
图11 转子位置、估计位置、电流

图12 实验系统
4 结论
本文以INFORM为理论基础,实现了嵌入式永磁同步电机在静止条件下的转子初始位置检测。该方法通过检测电流变化值,经过简单的计算,实现了初始位置的检测,该方法具有较强的工程性。
[1]沈建新,吕晓春,杜军红,等.无传感器无刷直流电机三段式起动技术的深入分析[J].微特电机,1998,26(5):8-11.
[2]唐灿伟.反电势感应技术在无刷直流电机控制中的应用[J].微电机,1998,31(6):16-19.
[3]谢宝昌.一种新颖无位置传感器控制盘式无刷直流电机研究[J].中小型电机,2000,27(1):8-11.
[4]Consoli A,Scarcella G,Testa A.Industry application of zero speed sensorless control techniques for pm synchronous motors[J].IEEE Trans.Ind.Appl.,2001,37(2):806-812.
[5]Erdman J M,Kerkman R J,Schlegel D W,et al.Effect of PWM inverters on AC motor bearing currents and shaft voltages[J].IEEE Trans.Ind.Appl.,1996,32(2):250-259.
[6]Teske N,Asher G M,Sumner M,et al.Suppression of saturation saliency effects for the sensorless position controlofinduction motordrives under loaded conditions[J].IEEE Trans.Ind.Electron,2000,47(5):1142-1150.
[7]Tanaka K,Yuzawa T,Moriyama R,et al.Initial Rotor Position Estimation for Surface Permanent Magnet Synchronous Motor[C].Industry Applications Conference,Thirty-Sixth IAS Annual Meeting,2001.
[8]Schroedl M.Sensorless Control of AC Machines at Low Speed and Standstillbased on theInform Method[C].IEEE IAS Annual Meeting San Diego,1996:270-277.
[9]Hua Y,Sumner M,Asher G,et al.Improved sensorless control of a permanent magnet machine using fundamentalpulse width modulation excitation[J].Electric Power Appl,2011,5(4):359-370.
[10]Gao Q,Asher G M,Sumner M,et al.Position estimation ofacmachinesoverawidefrequency range based on space vector PWM excitation[J].IEEE Trans.Ind.Appl.,2007,43(4):1001-1011.
[11]Ungurean A,Coroban-Schramel V,Boldea I.Sensorless control of a BLDC PM motor based on I-f starting and Back-EMF zero-crossing detection[C]. Optimization of Electrical and Electronic Equipment(OPTIM),2010 12th International Conference on DOI:10.1109/OPTIM.2010.5510578.

