波流耦合力对海洋平台桩腿楔块的影响

成 建，李永正，岳亚霖

(江苏科技大学，江苏 镇江212003)

0 引 言

20世纪以来，随着世界经济的快速发展，对于石油、天然气等自然能源的需求正不断增长，然而由于过往对于陆地资源过度开采，无法满足经济社会飞速的资源消耗，世界各国开始大力发展海洋资源。自升式海洋平台作为在海上进行钻井、采油、集运、观测、导航、施工等活动提供生产和生活设施的构筑物，对于海洋资源的开发起着十分重要的作用。然而自升式海洋平台承受波流耦合力等多种载荷的影响，平台结构失效和平台结构破坏时有发生。为了使得海洋平台安全使用寿命获得延长，对平台结构的研究需要不断深入。

本文以自升式海洋平台作为研究对象，通过Ansys 有限元软件对其进行结构强度分析研究。

1 自升式平台结构

由于受到各种海洋环境的考验，海洋平台在工作时受到风、浪、流等外部载荷的影响。诸如海洋平台楔块等结构构件面临不同程度的损耗过快、寿命低下的缺陷，需要频繁更换。为了保证海洋平台更加合理安全运作，对于目前自升式海洋平台的平台桩腿楔块需进行改进。考虑到波流耦合力对于海洋平台桩腿以及楔块的影响，通过研究自升式海洋平台受到的各种外载荷对于海洋平台楔块的影响，从而能够为海洋平台楔块性能得以改善奠定基础。

自升式平台由上层平台结构和下部桩腿结构组成，导管架底端通过桩基础固定。上层平台结构支撑框架和甲板，主要提供生产和生活场地，其外形为矩形，为了简化模型，尺寸为6 m ×6 m，水面至顶层甲板高度为6 m。本文只建立一个桩腿，组成空间结构。该海洋平台的主尺度为:圆桩结构的半径为3 m，桩腿高度为75 m;在平台与桩腿之间设置28个楔块，用于对桩腿的固定。

2 海洋平台有限元模型建立

由于本文主要研究波流耦合力对海洋平台楔块的影响，因此只建立一根海洋平台桩腿及其周围平台，但对于海洋平台桩腿周围楔块处进行相应的细化模型建立。

2.1 模型建立

本海洋平台模型由自升式海洋平台桩腿、海洋平台楔块和楔块接触处平台组成。其中依据实际情形，在固桩区以此建立28个海洋平台楔块。采用Ansys 软件建立海洋平台模型，并且根据重量报告调整结构模型重量中心位置。坐标系按照X 轴为纵向轴，尾部指向首部为正;Y 轴为横向轴，中心线指向左舷为正;Z 轴为垂向轴，基面向上为正。海洋平台模型如图1所示。

图1 海洋平台模型图Fig.1 Marine platform model

2.2 边界条件

1)固桩架下固桩平台(包括上固桩平台)平面内刚度远远大于桩腿局部结构刚度，可近似认为固桩平台原平面几何形状在力的作用下不变，即固桩平台对楔块支持为刚性支持。

2)为防止桩腿产生刚体位移，在桩腿与楔块的连接点给予垂向约束。

2.3 材料属性

本平台桩腿及海洋平台楔块都采用船用高强度钢D32。

2.4 工况

本文考虑波流耦合力对海洋平台楔块影响最大的自存和作业2 种海洋情况，分别进行桩腿楔块静力分析。另外针对这些结果，考虑平台分别服役在浪向分别在0°，60°，90°，120°，180°时的结构响应，对其结构进行相应研究。

3 强度分析

3.1 风载荷

在进行海洋石油结构物设计过程中使用的风速，应取决于长期的实测资料，本质上风载荷是动态的，但一些结构对它的反应几乎为静态形式。持续风速用于计算整个平台的风载荷，而阵风风速则用于单个结构构件的设计。

由于空气在一定速度下运动时，作用在平面和曲面上的理论风压力是空气的动能函数，因此可用数学关系式表示如下:

设承受风压的结构物投影面积为A，则可将总风力F 表示为:

式中:F为风载荷，N;K为风载荷形状系数，对梁及建筑物侧壁取1.5，对圆柱体侧壁取0.5，对平台总投影面积取1.0;KZ为海上风压高度变化系数，按规范取1.0;A为受风面积，m2;PO为基本风压，Pa。可按下式计算:

式中:α为风压系数，取0.163 N·S2/m4;νt为设计风速，m/s。

3.2 海流载荷

考虑到本平台作业水深，根据平台作业水深以及计算的波浪条件及波浪理论的适用范围，选择椭圆余弦波计算平台所受的波浪力。平台单腿柱所受的波浪力按Morison 公式进行计算，即:

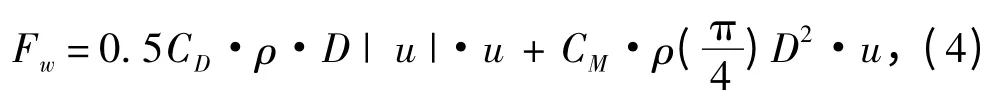
式中:ρ为海水密度，取ρ=0.1045 N·S2/m4;CD为垂直于构件轴线的曳力系数;CM为惯性力系数;D为圆形构件直径，m;u为垂直于构件轴线的水质点相对于构件的速度分量，m/s，| u|为其绝对值;u为垂直于构件轴线的水质点相对于构件的加速度分量，m/s2。

3.3 波浪力

波浪力是波动的海水作用于物体上的力，一般可以分为阻力、惯性力、撞击力、压差力和动量反射力5个主要的力。

对于自升式海洋平台波浪力的计算，是结构设计中最基本的任务，同时也是最困难的任务之一，因此一直以来都是海洋工程领域研究的重点。确定作用于自升式海洋平台上的波浪载荷，可以采用设计波法与随机分析法。

针对本文所研究的自升式海洋平台，流载荷按下式计算:

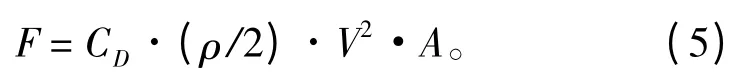
式中:v为计算流速，m/s;ρ为海水密度，kN·S2/m4;CD为垂直于构件轴线的流力曳力系数;A为构件在与流向垂直的平面上的投影面积，m2;

4 主要计算结果

4.1 波流耦合力

通过Ansys 有限元软件建立模型，考虑本自升式平台别服役在浪向分别在0°，60°，90°，120°，180°时结构响应，对其结构进行相应研究。首先探究波流耦合力与相位角之间的关系，如图2所示。

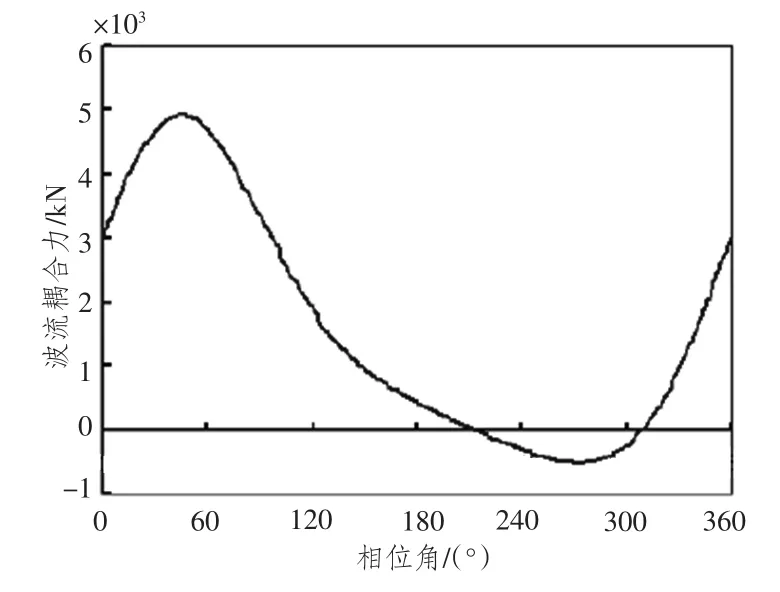
图2 波流耦合力－相位角关系曲线Fig.2 Wave bonding force-phase angle relation curves

4.2 静力分析

通过建立有限元模型，分析本海洋平台在不同工况下的结构相应，得到楔块在不同波流耦合力情况下受到的情形。其最大变形如图3所示。

图3 海洋平台楔块与桩腿接触处Fig.3 Offshore platform wedge contact with leg

图4 海洋平台楔块受力云图Fig.4 Offshore platform wedge stress nephogram

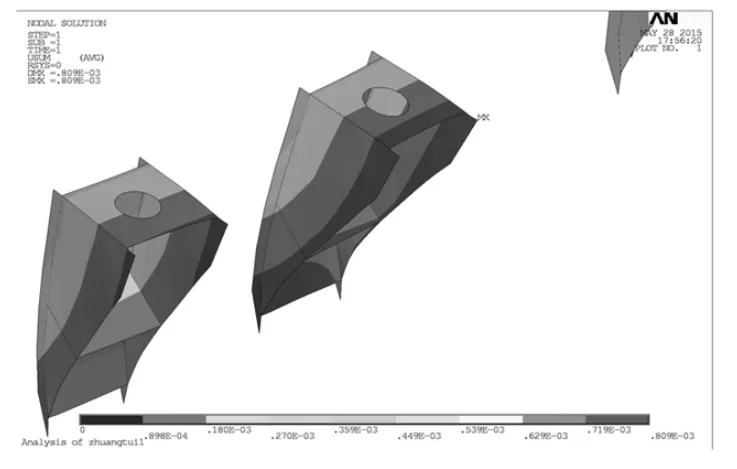
图5 海洋平台楔块最大变形处受力云图Fig.5 Offshore platform wedge maximum deformation stress

5 结 语

考虑到波流耦合力对于海洋平台结构构件的影响，本文结合海洋平台楔块实例分析，通过研究不同波流耦合力对于楔块的研究方法。探究理论研究和数值分析可以得到以下结论:

1)对于自升式海洋平台结构，采用Ansys 软件对于海洋平台楔块等结构构件建立具体模型研究。通过分析波流耦合力对其影响，可以有利于真实反映海洋平台细微处的疲劳损耗，对于具体工程有指导性作用。

2)由结果可知当随着相位角的改变波流耦合力的大小也随之改变，开始时随着相位角增大波流耦合力也随着增大，但当达到峰值后，随着相位角继续增加，波流耦合力却不断减小。

3)波流耦合力对海洋平台楔块有着十分重要的影响，由于实际海洋情况的变化，波流耦合力也不断变化，对于海洋平台楔块不断造成损耗。楔块的背部与平台相接处的地方受力最大，并且背面变形较大，造成海洋平台楔块寿命低下。

6 展 望

对于自升式海洋平台楔块所受波流耦合力的研究有助于对其后续结构性能改进提供理论基础。目前海洋平台楔块等小型结构构件面临着损耗过快、使用寿命低下等问题，然而楔块等结构构件对于海洋平台的安全性、经济性起到十分重要的作用。目前对于海洋平台楔块等结构构件基本采用简化方法，并不能很好地反应细微结构处受到的力的影响。我们不仅应当关注海洋平台整体结构性能，还要着眼于结构构件的改进，使得海洋平台能够更好地符合我国国情，为发展海洋事业，为我国开发与保护海洋资源做出更好地贡献。

［1］陈明璐，嵇春艳，刘珍.半潜式海洋平台的水动力分析及波浪载荷预报［J］.海洋技术，2012，31(4):72－74，78.CHEN Ming-lu，JI Chun-yan，LIU Zhen.Hydrodynamic analyois and wave lood forecast of semi-submersible platform［J］.Ocean Technology，2012，31(4):72－74，78.

［2］孙意卿.海洋工程环境条件及载荷［M］.上海:上海交通大学出版社，1989.

［3］刘海霞，肖熙.半潜式平台结构强度分析中的波浪载荷计算［J］.中国海洋平台，2003，18(2):1－4.LIU Hai-xia，XIAO Xi.Wave load calculation in the structural strength analysis of semi submersible platform［J］.China Sea Platform，2003，18(2):1－4.

［4］钱昆.浮体在大幅波浪中的运动和荷载计算研究［D］.大连:大连理工大学，2004.

［5］ABS.ABS rules for building and classing mobile offshore drilling units［M］.2008.