水下爆炸作用下计及冲击动弯矩的舰船总强度分析
李 烨,王 雷,陈莹玉,黄时春
(1.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨150001;2.哈尔滨船舶锅炉涡轮机研究所,黑龙江 哈尔滨150036)
0 引 言
就船体设计而言,对船体在各种海况状态下进行总强度校核时应该考虑尽可能多的可能出现的外载荷弯矩,从传统意义上而言外载荷弯矩一般包括中拱和中垂状态下的静水弯矩和波浪弯矩2 种[1]。因此通常情况下均以以上2 种弯矩作为总强度的主要考核对象。
根据中远场水下爆炸载荷特点,爆炸载荷主要包括冲击波载荷及气泡脉动载荷2 部分[2-3],冲击波主要造成船体局部损伤,而气泡脉动载荷则会导致舰船总体结构出现破坏[4-5]。实际上,军舰属于在战斗状态下需要承担作战任务的船舶,当其处于战斗环境中时,船体结构除了承受外部极端海况以外,还有可能遭受到水下武器的攻击。因此就舰船的总纵强度校核而言,计及水下武器的爆炸冲击对舰船产生的强度破坏十分必要。结合以往的海战实例以及实船爆炸试验可知,水下武器对舰船造成的总体破坏往往出现在气泡脉动阶段,轻者造成总体舰船设备和人员损伤,严重时使舰船丧失总纵强度甚至折断。这说明水下武器攻击舰船时会对舰船产生极大的总纵弯矩,而且该弯矩会贯穿整个冲击波和气泡脉动阶段,对舰船产生极大的总体破坏,通常称这种强破坏性载荷为水下爆炸冲击动弯矩[6]。
现有文献和研究成果对舰船计及水下爆炸冲击动弯矩下的总体强度进行讨论和研究相对较少。鉴于以上现状,本文针对某类典型水面舰艇的强度校核并结合各总强度规范提出的校核衡准数定义,对典型舰船的动弯矩重要性进行初步分析,以动弯矩时历曲线和动弯矩百分比重的形式展现冲击动弯矩在总强度校核中的重要性。通过数据定性地诠释在进行舰船总纵强度校核过程中加入动弯矩成分对于完善总强度分析的重要意义,更加客观地体现舰船在特殊战斗环境下的载荷状态及舰船生命力。
1 计算方法及数值模型
1.1 计算方法
根据水下爆炸载荷的特性,药包在水中爆炸后对舰船首先产生的冲击波可能会对舰船造成局部结构的破坏,而在冲击波之后的气泡脉动载荷则因脉动的“二次加载”而会对舰船的结构和设备造成总体破坏或者失效。关于冲击波和气泡脉动阶段的压力,一般由Geers-Hunter模型的估算公式[7]来确定:
在t <7Tc时(冲击波阶段),冲击波压力:

在t >7Tc时(气泡脉动阶段),气泡脉动压力:
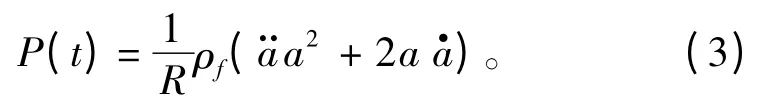
式中a 可由式(4)~式(8)联合求得:

式中:mc和ac分别为药包的质量和初始半径;Kc,K,k,r,A和B为材料常数;ρc为炸药的密度;ρf为流体密度;cf为流场中的声速;g为重力加速度;PI为爆心处流体静压;CD为经验流体阻力系数;Vc炸药的初始体积;R为测点到气泡中心的距离。
图1 给出某工况下根据Geers-Hunter模型和自编程序计算得到的冲击波和气泡脉动压力时历曲线(图中可见包括冲击波和2 次气泡脉动)。

图1 某工况冲击波和气泡脉动压力时历曲线Fig.1 Time history curve of shock wave and bubble pulse
在完成对载荷的计算以后,根据冲击波和气泡脉动载荷在流场和结构之间进行传递的特性,对典型舰船的水下非接触爆炸过程通过Abaqus 软件的流固耦合分析模块进行数值分析,通过将爆炸载荷在声学单元中的传播来完成载荷在流场和船体结构之间的传递,从而计算舰船结构的动响应。
本文所述冲击动弯矩的求解主要通过数值手段,在Abaqus 软件的inp 文件的输出部分设置命令“*Integrated Output,section =I-Section-1SOF,SOM”,其中“SOM”命令表示对冲击动弯矩的计算和输出,而“Section-1”则为所考核的动弯矩所在的剖面,且输出的弯矩方向和模型设置的方向需保持一致,剖面位置可由相应截面上的某个点的坐标进行确定。
在校核标准方面,大型水面战舰一般都对应存在相应的总强度校核标准。本研究在以极限弯矩为判据的基础上,参考了中国船级社,国军标GJB4000-2000 以及英国劳氏船级社等校核标准,根据各种标准存在的相应总强度安全衡准[8-11],结合本文对应的舰船的结构形式及作战环境表明,以国军标作为衡准更为符合舰船的实战环境特征。国军标规范中衡准阈值2.6 是综合多年舰船的总强度校核经验数值而设置,对于本文偏于安全。鉴于本文舰船的结构特性及材料性能方面拥有更高的强度,因此保留国军标的基本衡准表达形式符合总强度实际需求,同时在校核表达式中计及冲击动弯矩,对于舰船的总强度而言是偏于安全的。因此参考文献[6]在国军标表达式的基础上设定的安全衡准数c,以便对总强度分析提供定性的数据支持,c 由式(9)确定:
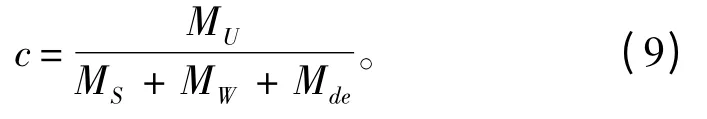
式中:MU为极限弯矩,MPa,极限弯矩根据GJB4000-2000 规范规定的极限弯矩计算方法进行计算;MS为静水弯矩,MPa,静水弯矩根据船体重力和浮力的分布情况对各纵向位置的剪力进行积分得到;MW为波浪弯矩,MPa,波浪弯矩根据中国船级社规定的基于船体梁理论的船舶极端中拱和中垂波浪弯矩估算公式进行计算;Mde为冲击动弯矩,MPa,根据Abaqus 软件的ODB 文件对典型剖面的弯矩输出得到。
1.2 数值模型
本文选取某典型水面舰船作为研究对象。模型采用大型有限元软件Ansys 按照1∶1实体建模。为使得模型尽可能地和实船保持一致,对于主要影响因素是质量的舰载设备而言,将其简化为质量点mass单元并布置在整船上以保证整船的质量分布与实船尽可能一致。同时考虑到舷外流场半径大小对舰船数值模拟精度产生的影响,本文采用流场半径是结构半径的6 倍[12-13],在减少计算量的条件下尽可能地减少系统增加的附加质量率,以保证计算精度。
对于船用材料,本舰船主要使用的是静态屈服极限超过450 MPa的945 钢。舰船有限元模型及其与流场耦合情况如图2所示。

图2 舰船有限元模型及与流场耦合示意图Fig.2 Sketch map of finite element model of ship coupling with fluid
2 工况设定
对于舰船的总纵强度分析而言,出现最大弯曲应力的典型剖面当属重点校核对象。因此根据舰船的一阶和二阶振型弯矩曲线,选取船长方向L/4,L/2,剖面作为动弯矩计算的典型剖面,3个主要校核剖面如图3所示。

图3 各典型剖面示意图Fig.3 Sketch of typical sections
设置的爆炸工况如下:药包当量1 000 kg TNT,爆距为0.15 L,3个典型位置处船中纵面正下方攻击。所有工况参数对应于表1。

表1 各工况设置表Tab.1 Parameters of explosive conditions
3 计算结果分析
舰船处于水下爆炸战斗工况时舰船结构已属于极端状态,且外力校核均以中拱中垂状态为标准。因此本章给出各工况下3个典型剖面位置的动弯矩时历曲线,同时列出各曲线对应剖面处中拱和中垂状态下的衡准数。
3.1 数值方法验证
鉴于本文主要采用数值的方法对舰船的动弯矩进行分析,因此有必要对动弯矩的数值精度进行相应简要的验证。
在基于力学方法计算动弯矩的过程中,一般把船体视为等值梁,根据船体各站剖面的惯性矩将船体简化为一船体梁,同时为确保模态吻合及计算模型的有效性,通常将原船各站重量以及船体产生附连水质量等效至船体梁模型上;同时,以压力载荷为基础,利用船体外壳单元的位置属性求出作用在船体外壳分布在各个站位上的激励力,以此作为船体梁计算的输入载荷;船体在受冲击载荷作用时必然出现吃水和浮力的改变,将船体因吃水变化而改变的浮力简化成弹簧模型,以刚度的形式模拟船体浮态带来的影响;最后利用Abaqus 求出船体梁在各载荷作用下的加速度及位移响应,作为求解冲击动弯矩的基本量。
爆炸载荷作用下船体主要受重力、浮力、爆炸载荷激励力及船体惯性力等综合作用。根据达朗贝尔原理并综合考虑各种力的作用,经编程可求解出各校核剖面的冲击动弯矩。
选取与本文研究对象排水量相近的舰船模型,设置典型工况并通过以上力学方法与数值方法对不同纵向位置的2个剖面(分别距离舯横剖面L1和L2,如图4所示)的无量纲动弯矩进行计算并对时历曲线进行对比,如图5所示。

图4 典型考核剖面Fig.4 Typical sections for assessing
由图5 中力学方法和Abaqus的数值方法进行比较可见,二者之间的整体趋势以及峰值大小吻合较好,误差较小,能较好地满足工程要求。

图5 剖面1和剖面2 动弯矩力学方法和数值方法对比Fig.5 Comparison of mechanics and numerical methods of impulse bending moment in section 1and section 2
3.2 典型爆点动弯矩曲线分析
3.2.1 爆点位于1/4 船长处
爆点位于1/4 船长处时3个典型剖面的爆炸冲击动弯矩时历曲线如图6所示。中垂和中拱极限条件下3个典型剖面衡准数由表2 给出。
由图6 可知,L/4 剖面的动弯矩波动最平缓,可能与爆点位置在L/4 位置有关。动弯矩峰值出现在气泡脉动阶段(约t = 1.1 s 左右),即气泡脉动能对舰船产生比冲击波更大的动弯矩。由表2 可知,在计及水下爆炸冲击动弯矩时衡准数的范围在1.6~3.9 之间,且中垂状态下衡准数明显大于中拱状态,在偏于危险工况条件下仍能保持较大的安全裕度。
3.2.2 爆点位于1/2 船长处
爆点位于1/2 船长处时3个典型剖面的爆炸冲击动弯矩时历曲线如图7 给出。表3 给出3个典型剖面在中垂和中拱极限条件下的衡准数。

图7 爆点位于L/2 时各典型剖面动弯矩时历曲线Fig.7 Time history curve of impact bending moment in typical sections of L/2 condition

表3 爆点位于L/2 时各剖面的中拱、中垂衡准数Tab.3 Sagging and hogging criterion numeral in typical sections of L/2 condition
3.2.3 爆点位于3/4 船长处
爆点位于3/4 船长处时3个典型剖面的爆炸冲击动弯矩时历曲线如图8所示。中垂和中拱极限条件下3个典型剖面衡准数如表4 给出。

图8 爆点于时各典型剖面动弯矩时历曲线Fig.8 Time history curve of impact bending moment in typical sections ofL condition
由图8 可知,L/4 剖面的动弯矩最小,L/2 剖面动弯矩整体最大且爆点位置附近剖面弯矩小于L/2 处。动弯矩峰值出现在气泡脉动阶段(约t = 1.1 s 左右),即气泡脉动能对舰船产生比冲击波更大的动弯矩。由表4 可知,计及水下爆炸冲击动弯矩时衡准数的范围在1.58~4.7 之间,中垂状态下衡准数明显大于中拱状态,在偏于危险工况条件下仍能保持较大的安全裕度。
表4 爆点位于时各剖面的中拱、中垂衡准数Tab.4 Sagging and hogging criterion numeral in typical sections ofcondition

表4 爆点位于时各剖面的中拱、中垂衡准数Tab.4 Sagging and hogging criterion numeral in typical sections ofcondition
剖面 中拱衡准数 中垂衡准数L/4 1.59 2.14 L/2 2.1 4.69 3 4 L 2.08 2.79
3.3 动弯矩比例分析
为了详细分析水下非接触爆炸作用下舰船水下爆炸冲击动弯矩对整个系统外载荷弯矩的影响状况,表5~表7 分别列出爆点在3个剖面时爆炸冲击动弯矩所占外载荷弯矩总和的百分比。其中外载荷弯矩包括静水弯矩、波浪弯矩以及水下爆炸冲击动弯矩。

表5 爆点L/4 处各剖面动弯矩占外载荷弯矩总和比例(109 N·m)Tab.5 Percentage of impact bending moment in typical sections of L/4 condition

表6 爆点L/2 处各剖面动弯矩占外载荷弯矩总和比例(109 N·m)Tab.6 Percentage of impact bending moment in typical sections of L/2 condition
表7 爆点处各剖面动弯矩占外载荷弯矩总和比例(109 N·m)Tab.7 Percentage of impact bending moment in typical sections of condition

表7 爆点处各剖面动弯矩占外载荷弯矩总和比例(109 N·m)Tab.7 Percentage of impact bending moment in typical sections of condition
剖面位置 中拱外载荷弯矩总和中拱冲击动弯矩中拱动弯矩比例/%中垂外载荷弯矩总和中垂冲击动弯矩中垂动弯矩比例/%L/4 剖面1.57 0.9498 60.5 1.166 0.9473 81.24 L/2 剖面 1.655 0.5479 33.1 0.74 0.4941 66.77 3 4 L 剖面1.288 0.7466 57.96 0.958 0.5411 56.48
由表5~表7 中百分比数据可知,水下爆炸冲击动弯矩在外载荷弯矩中的比重达到50%~80%,部分剖面甚至超过80%,对舰船总体弯矩影响非常大,即冲击动弯矩对系统的影响不容忽视。
同时,通过对表中各工况下3个典型剖面的冲击动弯矩与舰船结构外载荷弯矩总和的比值进行比较分析可以看出,爆点在船体首尾L/4 时各剖面动弯矩所占百分比比较接近,且同一爆点对应工况下L/4和剖面弯矩均明显大于L/2 剖面;而当爆点在船中L/2 处时,船中剖面动弯矩比例明显大于艏尾L/4 剖面处的弯矩百分比。且中拱状态下的动弯矩明显大于中垂状态,产生此种现象的原因可能与中拱是由爆炸冲击波直接作用的结果有关。
4 结 语
通过对典型舰船应用有限元软件Abaqus的声固耦合算法对舰船在水下非接触爆炸下的结构响应进行数值模拟,获得了在不同工况下的总体结构响应,对典型剖面的水下爆炸冲击动弯矩进行分析并得出以下结论:
1)各工况下,水下爆炸冲击动弯矩和舰船外载荷弯矩总和处于同一数量级上,对舰船的弯矩影响非常大,对舰船的总体结构强度的影响不容忽视。
2)综合各工况,在计及水下爆炸冲击动弯矩时衡准数的范围在1.5~4.7 之间,即本舰船在偏于危险条件下仍能保持足够大的总纵强度安全裕度。
3)在所有工况中,L/4 剖面的动弯矩整体最小,且同一典型剖面在远离爆点位置时相比遭受正下方爆炸冲击情况下动弯矩响应要大。爆点位于L/4 位置时应注意舰船总体二阶振型引起的首尾L/4 处较大的动弯矩;当爆点位于L/2 位置时应足够重视舰船总体一阶振型引起的L/2 处较大的动弯矩。
[1]王福花,朱胜昌,陈庆强.水面舰船总强度标准应用研究[J].船舶力学,2004,8(4):95-100.WANG Fu-hua,ZHU Sheng-chang,CHEN Qing-qiang.Study on hull-girder strength criteria of naval ships[J].Journal of Ship Mechanics,2004,8(4):95-100.
[2]GEERS T L.Excitation of an elastic cylindrical shell by a transient acoustic wave[J].App1y.Mechs,1969,36:459-469.
[3]GEERS T L.Doubly asymptotic approximations for transient motions of submerged structures[J].The Journal of the Acoustical Society of America,1987,64:1500-1508.
[4]ZHANG A-man,ZHOU Wei-xing,WANG Shi-ping,et al.Dynamic response of the non-contact underwater explosion on naval equipment[J].Marine Structures,2011(24):396-411.
[5]张弩,于馨.水下爆炸冲击波与气泡载荷作用下船体结构的动响应[J].中国舰船研究,2014,9(1):99-104.ZHANG Nu,YU Xin.Dynamic response of a hull structure subjectedto underwater explosion shock wave and bubbles[J].Chinese Journal of Ship Research,2014,9(1):99-104.
[6]岳永威.大型运输船水下爆炸结构强度计算方法研究[D].哈尔滨:哈尔滨工程大学,2013.
[7]GEERS T L.Doubly asymptotic approximations for transient motions of submergedstructures[J].The Journal of the Acoustical Society of America,1987,64:1500-1508.
[8]中国船级社.钢质海船入级与建造规范[M].北京:人民交通出版社,2006.
[9]GJB4000-2000,极限弯矩校核船体总纵强度[S].2006.
[10]英 国 劳 氏 军 用 规 范.Rules and Regulations for the Classifiation of Naval Ships,2008.
[11]ZHANG A-man,ZENG Ling-yu,CHENG Xiao-da,et al.The evaluation method of total damage to ship in underwater explosion[J].Applied Ocean Research,2011,33:240-251.
[12]ZHANG A-man,WANG Shi-ping,HUANG Chao,et al.Influences of initial and boundary conditions on underwater explosion bubble dynamics[J].European Journal of Mechanics B/Fluid,2013,42:69-91.
[13]姚熊亮,徐小刚,张凤香.流场网格划分对水下爆炸结构响应的影响[J].哈尔滨工程大学学报,2003,24(3):237-244.YAO Xiong-liang,XU Xiao-gang,ZHANG Feng-xiang.Influence of fluid gridding on structural responseof underwater explosion[J].Journal of Harbin Engineering University,2003,24(3):237-244.

