基于自回归滑动平均模型的风电功率预测
基于自回归滑动平均模型的风电功率预测
党睿,张俊芳
(南京理工大学自动化学院,南京210014)
摘要:针对风电功率的波动性及不可控性等问题,提出基于自回归滑动平均(ARMA)模型的风电预测方法。基于风速序列的时序性和相关性建立ARMA模型,利用该模型进行风电功率的预测。结合某风电厂的风电数据对该预测模型进行分析和验证,结果表明,提出的基于ARMA模型的风电预测方法能够有效地对风电功率进行预测。
关键词:风电功率;自回归滑动平均模型;风电预测
随着经济高速发展和环境问题日益突出,风力发电已经成为当前一个研究热点。风电是具有间歇性、波动性的电源[1],其大规模的并网会给电网的安全稳定运行带来新难题。因此研究风电功率的波动特性并建立有效的风电功率预测模型对于发展风力发电具有重要的意义[2]。
目前国内外学者对风电功率和风速的预测方法进行了大量研究。主要的风电功率预测预报方法有物理方法、时间序列法、神经网络法、小波分析法和组合模型法等,对于不同的预测模型或算法,其精度不同,适用的情况也不尽相同。其中,时间序列法[3]的最大特点是对风速数据的依赖性较低,能利用有限的风速样本便可取得较出色的预测效果。该方法利用历史风速数据或历史风电功率数据进行分析和建立预测模型[4],建模时所需的信息少且运算方便,因此得到广泛应用[5]。自回归滑动平均(ARMA,Auto-regressive and Moving Average)模型是时间序列模型之一,其在最小方差意义下对平稳时间序列进行逼近预报,尤其在数据统计不完善的情况下更有效[6]。本文在研究ARMA模型的基础上,结合某风电厂的实际风电数据建立基于ARMA的风电预测模型,并对该模型进行分析和验证。
1 ARMA模型
1.1ARMA模型的基本形式
自回归滑动平均模型(ARMA)将随时间推移而形成的数据视为一个随机时间序列,该序列中第t个时刻的值不仅与(t-1)时刻的值有关,且与(t-1)时刻的随机干扰量有关,由此建立模型对未来值进行预测[7]。对于(p,q)阶自回归滑动平均模型可表示为
式中:Yt为时间序列t时刻的值;φi为自回归参数;θj为滑动平均参数;ut为时间序列t时刻随机干扰量,构成一个白噪声序列;p为自回归阶数;q为滑动平均阶数。该模型可记为ARMA(p,q)。
当q=0时,ARMA(p,0)模型就是p阶自回归模型(简称AR(p)模型)
当p=0时,ARMA(0,q)模型即q阶滑动平均模型(简称MA(q)模型)
可见,AR模型和MA模型本质上是ARMA模型[8]。其中AR(p)模型是对系统自身过去状态的反映,MA(q)模型则是用来对噪声序列的影响作采集分析。
1.2ARMA模型的建立
ARMA模型是建立在对时间序列进行逐步分析的基础上,主要包含以下关键内容。
(1)时间序列的平稳性分析
ARMA模型要求主体部分的时间序列必须是平稳的[9],在建模前需对采集的时间序列做平稳性检验;对于非平稳的时间序列,则需通过差分处理将其平稳化。时间序列的平稳性通过ADF单位根检验来判断。
Eviews是1款用于从事数据分析、回归分析和预测的软件,采用该软件可方便地对时间序列进行ADF单位根检验,依据计算结果可判断时间序列的平稳性。一般情况下,比较ADF统计量与显著性水平5%下的临界值,若ADF统计量比检验的临界值小,单位根不存在,表明原始序列为平稳序列;若ADF统计量比检验的临界值大,则单位根存在,表明原始序列为非平稳序列。
(2)模型的识别
对于平稳的时间序列{Yt},根据其自相关函数(ACF)和偏相关函数(PACF)的数值变化趋势可以判断在AR模型、MA模型、ARMA模型中采用何种模型建模最为合适[10]。
当k大于q恒有p̂k等于0时,称自相关函数是“截尾”的;若无论k取多大,p̂k保持逐渐衰减且恒取非零值,则称自相关函数是“拖尾”的。同理可判断偏相关函数是“截尾”还是“拖尾”的。根据自相关函数和偏自相关函数是否呈现拖尾或截尾的性质可对模型进行识别,判断准则[11]如表1。
3)模型的定阶及参数估计
模型的定阶即确定自回归阶数p和滑动平均阶数q。通过对时间序列样本作自相关和偏自相关分析,利用自相关和偏自相关曲线确定模型的阶数,然后选择若干不同阶数的模型进行分析,根据最小信息准则(AIC准则)对模型进行定阶[12]。
AIC准则的函数表达式为
式中:Z为AIC函数值;σ2为模型残差序列的方差估计值;N为样本长度。Z越小,表示其拟合效果越好。选择Z值最小的模型,并采用最小二乘估计法进行参数估计,即在已知样本序列值的条件下,采用非线性的最小二乘法求出使残差平方和达到最小的自回归参数和滑动平均参数。
4)模型的适用性检验
ARMA模型中,参数估计的基础是假设随机扰动量为白噪声序列。白噪声的检验通过自/偏相关函数和Q统计量来完成。若残差序列非自相关,则残差是白噪声序列,所建模型是有效的。模型建立的基本流程如图1。
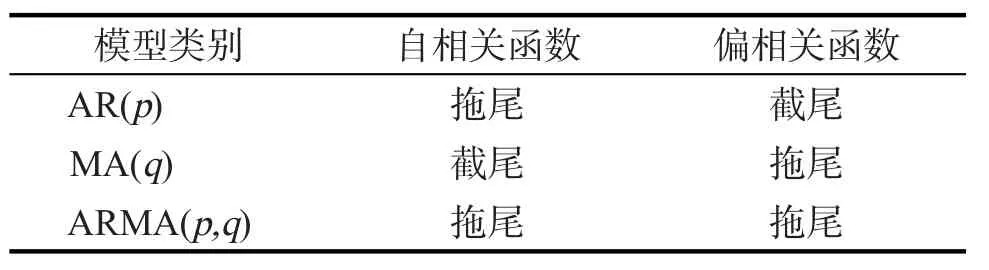
表1 模型的识别准则Tab. 1 Identification criteria of the model
2 风电功率预测与分析
2.1原始风速数据
选取我国某风电场1月1日至1月7日的历史风速序列,数据采样间隔为5 min。利用Eviews软件进行ARMA模型的搭建。导入采集的风速时间序列样本,样本数据显示如图2。
2.2数据的处理及模型的建立
(1)原始风速时间序列的平稳性检验
利用ADF单位根检验判断风速序列是否平稳,若风速时间序列存在单位根则说明序列是非平稳的,反之说明序列是平稳的。对风速时间序列进行ADF单位根检验的结果如表2。
由表2可见,原始风速序列在显著性水平5%的条件下,ADF统计量小于单位根检验的临界值,说明单位根不存在,表明原始序列为平稳序列,不需进行差分处理。
(2)模型的识别

表2 风速序列ADF检验结果Tab. 2 ADF test results of the wind series
对前6天的风速序列按式(4),(5)计算自相关系数和偏自相关系数,结果如图3。由图3可见,风速序列的自相关系数呈逐渐减小的拖尾趋势,偏自相关系数呈明显的截尾特征,根据表1的识别准则,初步将模型确定为AR(p)模型。
3)模型的定阶及参数的估计
选取若干不同的p值对AR(p)模型进行分析后定阶,取AIC值最小的模型作为最佳拟合模型。由于偏自相关系数在四阶后开始明显趋近于零,故可令p=2,3,4,5分别计算AIC值,并采用最小二乘估计法对模型进行参数估计,计算结果如表3。
由表3可见,AR(4)模型的AIC值最小,根据模型定阶的AIC准则,将风速时间序列模型定为四阶自回归模型,即AR(4)。因此得到预测模型

表3 AR(p)模型参数拟合结果Tab. 3 Parameter fitting results of AR(p) model
4)模型的适用性检验
确定模型为AR(4)模型,对建模产生的残差序列作随机性检验,以验证模型的有效性。残差序列的相关性如表4。
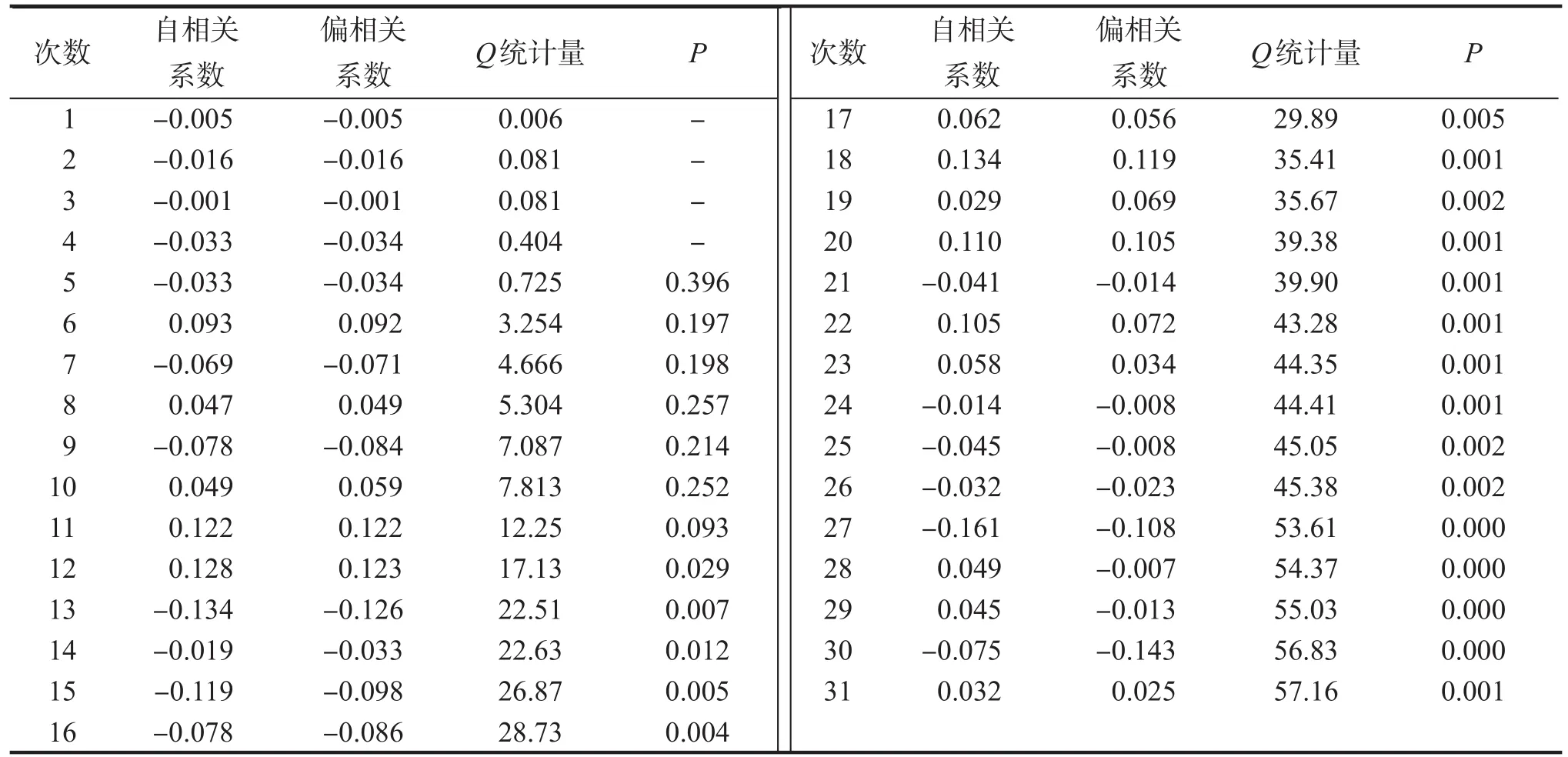
表4 AR(4)模型残差序列的相关性Tab. 4 Correlation of residual sequence of AR(4) model
从表4可看出:残差序列的自相关系数及偏相关系数趋近于0,残差序列表现为非自相关,认为残差是白噪声序列;残差序列在滞后期数大于11后其Q统计量的P(概率)开始趋近于0,即样本差异由抽样误差所致的概率趋近于0,说明残差序列为白噪声的概率较大;残差序列的Q统计量P稳定在低水平,近似表明残差序列为白噪声。因此,从最后残差序列的相关性结果可近似认为该序列是白噪声序列,表明所建模型有效。
2.3模型预测结果分析
根据所建AR(4)模型,利用风电场前6天的实际风速数据对第七天的风速进行预测,采样间隔为5 min,预测结果如图4。从图4可见,第七天的预测风速曲线与实际风速曲线基本拟合,对比风速的预测值和实际值可得,ARMA模型预测值的平均误差为12.4%,最大误差为15.6%。
风电场中风力发电机组根据风速发电,对应的各风电机组的风电功率的预测值与实际值的对比结果见图5。从图5可见,基于ARMA模型的风电预测功率和实际功率基本吻合,误差较小。表明在风电场功率数据统计不完善的情况下,可以利用风电场的风速原始数据构建基于ARMA模型的风电功率预测模型,通过该模型能有效对风电功率进行间接地预测。
3 结 论
针对风电场的风速数据并结合时间序列理论建立基于ARMA的预测模型。通过该模型对风速时间序列进行预测,间接对风电功率预测。通过某风电场实际风功率预测,结果表明基于ARMA的风功率预测模型不仅在风电场功率数据统计不完善的情况下能够有效利用风速原始数据间接地预测风电功率,而且预测精度较高。
参考文献:
[1]谷兴凯,范高锋,王晓蓉,等.风电功率预测技术综述[J].电网技术,2007, 31(S2):335-338.
[2]范高锋,裴哲义,辛耀中.风电功率预测的发展现状与展望[J].中国电力,2011, 44(6):38-41.
[3]薛禹胜,郁琛,赵俊华,等.关于短期及超短期风电功率预测的评述[J].电力系统自动化,2015, 39(6):141-151.
[4]洪翠,林维明,温步瀛.风电场风速及风电功率预测方法研究综述[J].电网与清洁能源,2011, 27(1):60-66.
[5]王国权,王森,刘华勇,等.风电场短期风速预测方法研究[J].可再生能源,2014, 32(8):1134-1139.
[6]潘迪夫,刘辉,李燕飞.风电场风速短期多步预测改进算法[J].中国电机工程学报,2008, 28(26):87-91.
[7]甘晖.烧结终点预测的应用研究[J].安徽工业大学学报(自然科学版),2010, 27(3):299-304.
[8]李瑞莹,康锐.基于ARMA模型的故障率预测方法研究[J].系统工程与电子技术,2008, 30(8):1588-1591.
[9]黄永兴.我国股价指数的时间序列模型研究[J].安徽工业大学学报(自然科学版),2002, 19(4):336-340.
[10] Hong Y, Chao M H. A new short-term load forecasting approach using self organizing fuzzy ARMA model[J]. IEEE Transon Power systems, 1998,13(1):217-225.
[11]程引,刘静伟,赵晋泉.基于ARMA模型的中短期风电功率预测[J].水电与新能源,2012, 103(4):72-75.
[12]邵璠,孙育河,梁岚珍.基于ARMA模型的风电场风速短期预测[J].电网与清洁能源,2008, 24(7):52-55.
责任编辑:何莉
Wind Power Prediction Based on Auto-regressive and Moving Average Model
DANG Rui, ZHANG Junfang
(School of Automation, Nanjing University of Science & Technology, Nanjing 210014, China)
Abstract:In view of the fluctuation and uncontrollability of wind power, a method of predicting wind power based on auto-regressive and moving average (ARMA) model was put forward. ARMA model was established based on the timing and correlation of wind speed sequence, and the prediction of wind power was implemented by using the model. The prediction model was analyzed and verified with wind power data of a wind power plant. Results show that the proposed wind power prediction method based on ARMA model can effectively predict the wind power.
Key words:wind power;ARMAmodel; prediction of wind power
通信作者:张俊芳(1965-),女,陕西武功人,副教授,主要研究方向为电力系统优化、运行与控制。
作者简介:党睿(1993-),男,山东商河人,主要研究方向为电气工程及其自动化。
基金项目:国家自然科学基金项目(61203129)
收稿日期:2015-05-12
文章编号:1671-7872(2015)-03-0273-05
doi:10.3969/j.issn.1671-7872.2015.03.014
文献标志码:A
中图分类号:TM715

