混凝土坝变形滞后特征及坝型对其的影响研究
张家鹤,王 建,柴丽莎
(河海大学水利水电工程学院,江苏省南京市 210098)
混凝土坝变形滞后特征及坝型对其的影响研究
张家鹤,王 建,柴丽莎
(河海大学水利水电工程学院,江苏省南京市 210098)
混凝土坝温度变形呈周期性变化,其相位滞后于气温,该现象通常被解释为由于混凝土导热系数小、热传导慢而引起,但该解释并不全面。本文运用热学与力学基本理论,推导了计算悬臂梁及拱圈温度变形滞后时间的解析公式,并据此研究坝型对滞后的影响,得到以下结论:坝内平均温度的滞后时间大于温度梯度的滞后时间;坝型对滞后时间有较大影响,拱坝水平位移的滞后时间比重力坝要长。
混凝土坝;滞后;温度;解析解
0 引言
监测资料分析是大坝健康诊断的重要内容之一,国内外对此也一直在开展研究[1-3]。在混凝土坝变形监测资料分析中,一般将整个变形分解为水压分量、温度分量和时效分量[4-6]。其中,温度分量反映了大坝在外界温度变化作用下的变形,而且,温度分量的相位与气温相比有滞后现象,如图1(a)所示。
对于上述滞后现象,通常的解释是由于坝体导热系数小、热传导慢而引起。但笔者在实践中发现:导热系数和坝厚接近的大坝,其水平位移的滞后时间也可能存在较大的差异,而且厚度较薄的拱坝的位移滞后时间常常比厚度大的重力坝更长。例如,图1(b)给出了水口重力坝及李家峡双曲拱坝的滞后时间沿铅直方向的分布,可以看出,尽管李家峡拱坝相对较薄,但其滞后时间却明显高于相对较厚的水口重力坝。由此可见,仅仅考虑坝体导热系数小、热传导速度慢这一因素,难以充分解释上述现象。
本文运用热学与力学基本理论,推导了计算悬臂梁及拱圈温度变形滞后时间的解析公式,并从坝型角度入手,对滞后原因给出进一步的分析阐述,实现概念上的澄清和深化,为大坝健康诊断提供理论支持。
1 混凝土坝准稳定平均温度及线性温差
由于混凝土坝主要是以上下游坝面为边界进行热传导的,与无限大平板沿厚度方向的一维热传导较为接近。为此,下面以无限大平板内的准稳定温度分布为依据进行分析。如图2所示,无限大平板厚度为L,侧面温度作余弦变化,板内温度只沿厚度方向变化,热传导方程为:
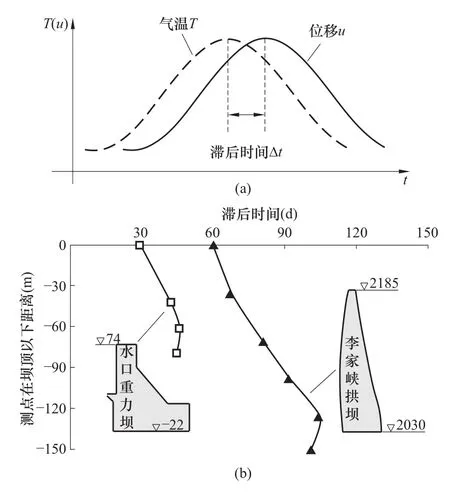
图1 位移滞后及其随测点位置的分布

边界条件为:
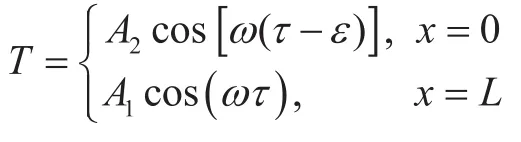
式中:A1、A2为边界温度变幅;w为温度变化圆频率;e为边界x=0处的温度滞后于x=L处温度的时间。
温度变形和温度应力分析时,习惯上将板内温度分解为平均温度Tm以及沿厚度方向的线性温差Td和非线性温差Tn。对于变形不受约束的自由板,Tm和Td分别引起板的拉伸变形和转动;而非线性温差则对变形没有影响,仅引起温度应力。因此,对混凝土坝变形滞后分析来说,仅需分析Tm和Td的影响,计算公式如下[7]:
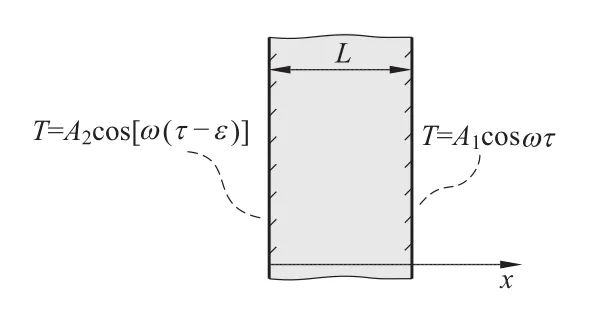
图2 自由板

式中:
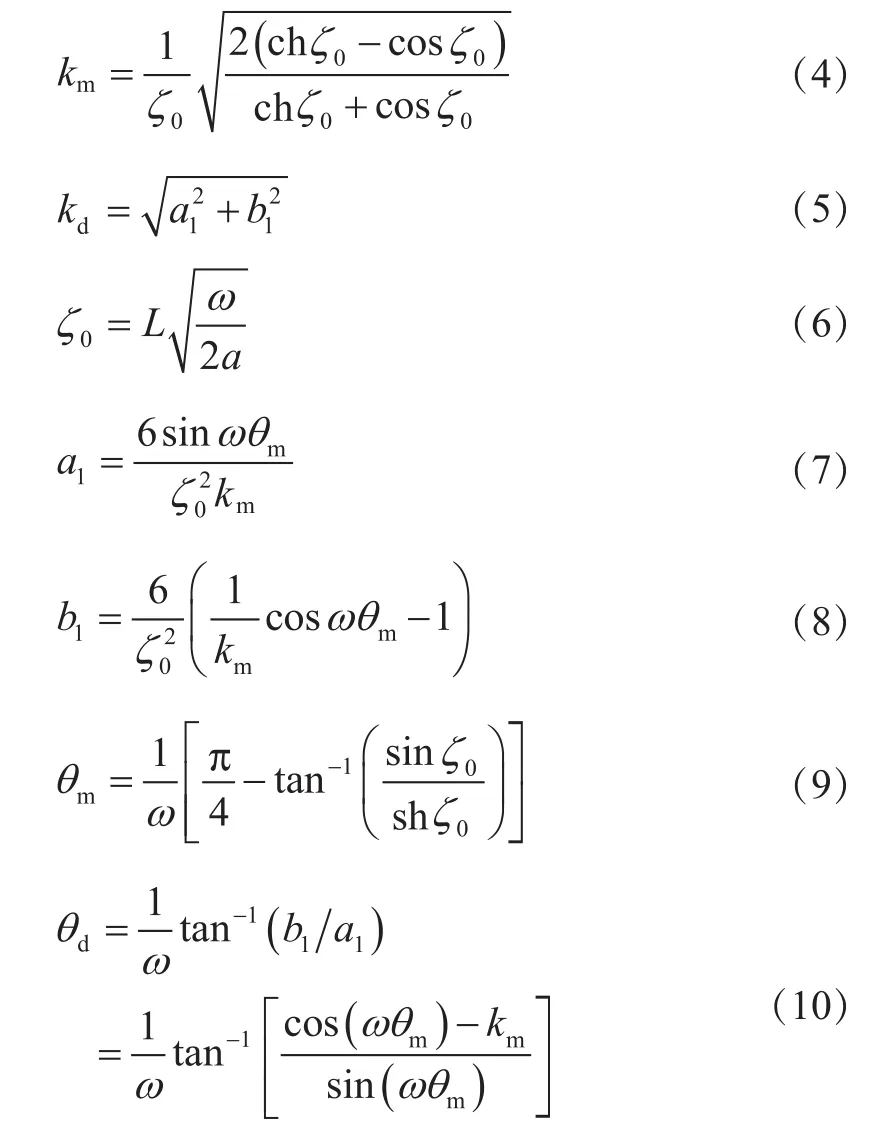
根据式(2)、式(3)可知:qm和qd代表了平均温度Tm和线性温差Td滞后于边界温度的时间。为简单起见,这里首先假设式(2)和式(3)中的e为0,计算滞后时间qm和qd与板厚L及导温系数a之间的关系,如图3所示。计算时,导温系数取值范围在0.05~0.15m2/d之间,涵盖了混凝土导温系数的常见范围;外界环境温度变化周期取365d,即圆频率w=2p/365。
由图3可以看出:
(1)qm>qd,即平均温度的滞后时间比线性温差的滞后时间长。该特征决定了拱坝水平位移的滞后时间比重力坝要长,这一点将在后文详细论述。
(2)平均温度的滞后时间qm将随板厚的增加而迅速趋于常数0.25p/w。这是由于板厚L与z0成正比关系,而双曲正弦函数shz0随z0的增加而迅速增加,因此,根据式(6)和式(9)可知,qm将趋于0.25p/w。该特性表明平均温度的滞后时间qm不会随板厚的增加而一直增加,当板厚超过15m以后,qm将基本保持不变。
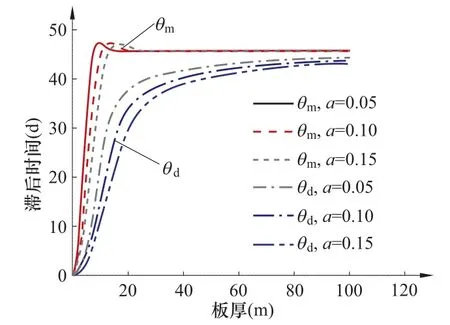
图3 平均温度和线性温差的滞后时间与板厚及导温系数的关系
(3)线性温差的滞后时间qd随板厚L的增加而增加。这是由于chz0随z0的增加迅速增加,因此km趋于,而z0板厚与L成正比,因此km随板厚L的增加而下降;同时根据结论(2)有qm趋于常数,因此,根据式(10),线性温差的滞后时间qd随板厚L的增加而增加。
2 滞后时间计算的解析公式
为简单起见,这里分别以重力坝和拱坝的顺河向水平位移为例,推导求解变形滞后时间的解析公式,并对其特征进行对比分析。
2.1 重力坝滞后时间的解析公式
重力坝在力学上可看做悬臂梁。因此,这里以高为H,底厚为B的三角形悬臂梁的变形为例,分析其单侧受变温作用下坝体水平位移特征,如图4所示。
根据虚功原理,整体变形时在拱坝上引起的某一总位移可由每个微段变形在该处引起的位移dΔ积分得到,即:
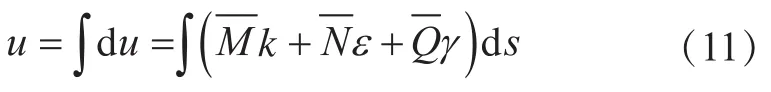
式中:k、e和g分别为微元体的曲率、轴向应变和剪切应变;分别为虚设单位荷载引起的微元体的弯矩、轴力和剪力。
对高度h处的P点来说,由变温引起的水平位移计算公式为:
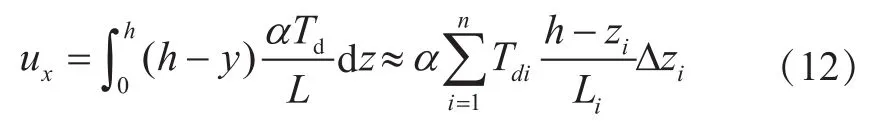
式中:a为线膨胀系数;n为使用求和代替积分所采用的分割数;zi、Li和Δzi分别为第i层分割对应的高度、坝厚及微元高度。
根据式(12)可知,重力坝的坝顶水平位移与线性温差之间为线性关系。
将式(3)代入式(12)后利用三角函数变换(积化和差),则式(12)可改写为:

将式(13)进行三角函数变换(和差化积)后得到:
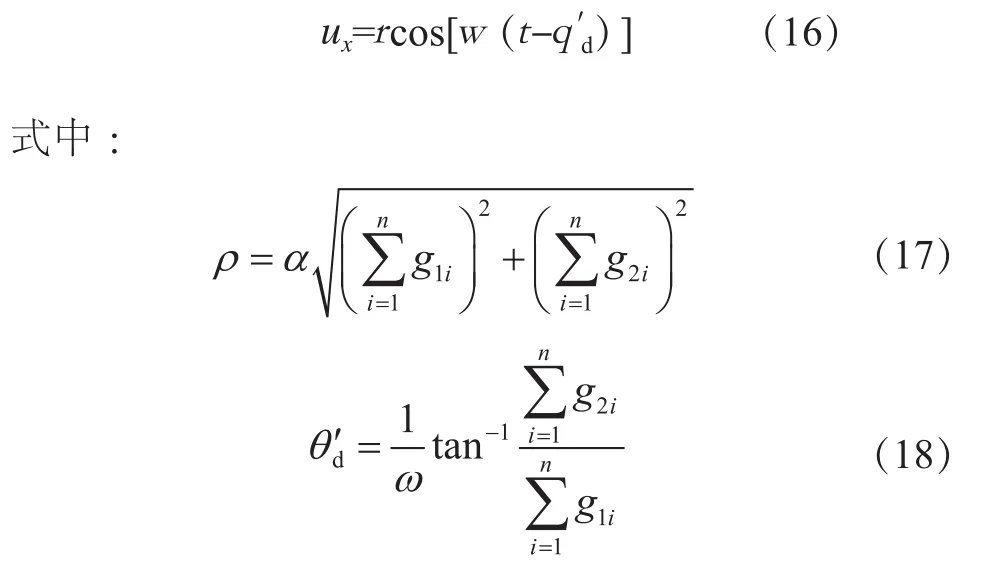
由式(16)容易看出,q′d即为P点的滞后时间。
2.2 拱坝滞后时间的解析公式
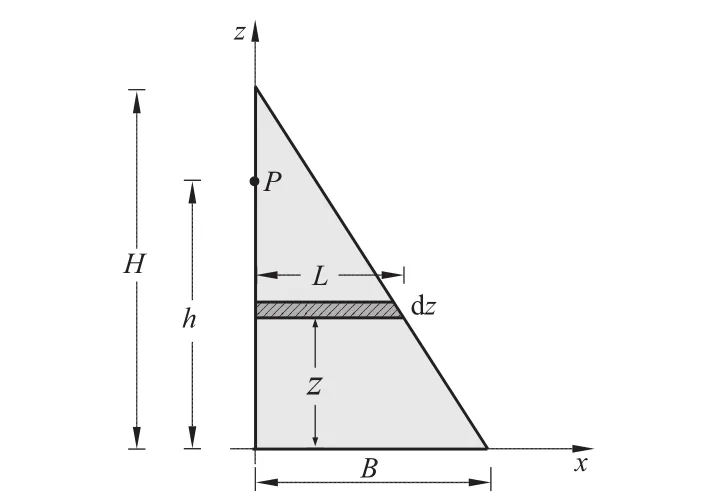
图4 重力坝变形计算示意
拱坝是空间超静定结构,其力学响应可以分解为拱作用和梁作用,其中拱作用对变形的影响占主导地位。因此,这里取单层拱圈按纯拱法进行分析,如图5所示,其中,中心角为2j,半径为R。

图5 拱圈受力分析
运用式(11)并根据拱冠处转角及切向位移为零这一对称条件,可以求出由温度荷载Tm、Td作用引起的拱冠处的轴力N和弯矩M,进一步求出由Tm、Td引起的径向位移,其值为:
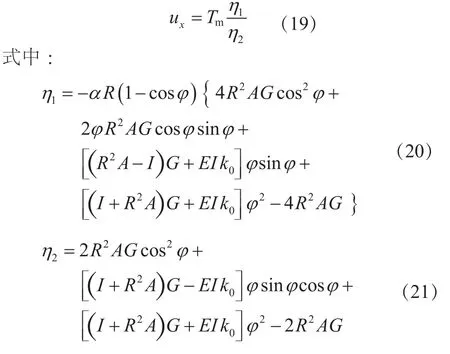
式中:E、G分别为材料弹性模量和剪切模量;A、I分别为面积和截面惯性矩;k0为与截面形状有关的无量纲参数,对于矩形截面,k0=1.2。
由式(19)~式(21)可以看出,拱圈径向位移与平均温度Tm成正比,与线性温差Td无关。对于切向位移而言,存在相同的结论;同时,位移滞后时间与平均温度Tm的滞后时间相同,即为式(2)中的qm。
3 坝型对滞后时间的影响
对比拱坝与重力坝可知,由于两者在结构响应上的区别,即重力坝坝顶水平位移的滞后时间取决于线性温差,而拱坝的滞后时间主要取决于平均温度,导致了拱坝水平位移的滞后时间总体上比重力坝要长,原因见前文第1部分的分析结论。
为直观起见,按取式(2)和式(3)计算了坝高100m的重力坝和拱坝的滞后时间并绘制曲线,如图6所示。计算时,重力坝坝底厚度取70m,拱坝坝底厚度取35m,坝顶厚度均取8m,混凝土导温系数取0.1m2/d;同时,取式(2)和式(3)中的e为0,即暂时不考虑边界温度滞后的影响,此时式(2)和式(3)中的A1、A2取值对滞后时间的计算结果没有影响。
由图6可以看出,尽管拱坝的厚度要小于重力坝,但其滞后时间却比重力坝要长。当然,以上分析中没有考虑梁效应对拱坝变形滞后时间的影响,实际上由于梁效应的存在,拱圈变形滞后时间可能会略有缩短。但由于拱效应占主导地位,因此 “拱坝水平位移的滞后时间总体比重力坝要长”这一结论仍然成立。

图6 重力坝与拱坝滞后时间对比(e=0)
4 结论
混凝土坝水平位移温度分量的相位与气温相比有滞后现象,通常的解释是由于坝体导热系数小、热传导速度慢而引起,但该解释不够全面。本文基于热学和力学基本理论,从热传导速度以及坝型等角度,对该现象进行了较为深入的研究,从概念上进行澄清和深化,为大坝健康诊断提供基础理论支持。主要成果和结论如下:(1)推导了悬臂梁及拱圈滞后时间的解析公式,并与有限元计算结果进行了对比验证。
(2)坝型对滞后时间有较大影响,拱坝水平位移的滞后时间总体比重力坝要长,这是因为拱坝变形的滞后时间主要取决于坝体平均温度,而重力坝则主要取决于坝内温度梯度。
由于文章篇幅限制,水温滞后e对位移滞后时间的影响以及位移滞后时间分别沿高程和坝厚两方向上的分布情况将在另文进行分析说明。
最后应说明,本文主要是针对水平位移开展研究的。对于垂直位移,可采用类似的方法进行研究。例如,对于重力坝,其垂直位移主要由于铅直向膨胀或收缩引起,其滞后时间主要取决于坝体平均温度的滞后时间,这一点与水平位移不同,具体不再赘述。
[1] Wu Z R,Li J,Gu C S,et al,Review on hidden trouble detection and health diagnosis of hydraulic concrete structures.Sci China Ser E-Tech Sci,2007,50: 34–50.
[2] 李珍照.国外大坝监测分析的新进展[J].水力发电学报,1992,37:75-84.
[3] 张进平,黎利兵,卢正超.大坝安全监测研究的回顾与展望.中国水利水电科学研究院学报,2008,6:317-322.
[4] Fanelli M,Giuseppetti G.Safety monitoring of concrete dams.Water Power Dam Constr,1982,34:31-33.
[5] 吴中如.水工建筑物安全监控理论及其应用.北京:高等教育出版社,2003.
[6] 顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社,2006.
[7] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1998.
张家鹤(1991—),男,硕士研究生,主要研究方向:大坝安全监控与SPH无网格法数值模拟。E-mail: zhangjh_hhu@163.com
Research on the Hysteresis Characteristic of Concrete Dam Deformation and the Influence of Dam Types
ZHANG Jiahe,WANG Jian,CHAI Lisha
(Hohai University,Nanjing 210098,China)
The thermal deformation of a concrete dam changes periodically; and its phase lags behind the air temperature.This phenomenon is often interpreted as due to the low velocity of heat conduction in concrete,but this interpretation is not comprehensive. Based on the fundamental theories of thermal mechanics,firstly this paper derives the analytical solutions for the computation of hysteresis time of thermal deformation for cantilever beam and arch ring,and then applies them to study how the factors including dam type,reservoir water temperature and spatial position affect the hysteresis time.The following conclusions are obtained: the hysteresis time of the mean temperature is greater than that of the temperature gradient; the dam type has a great impact on the hysteresis time,and the hysteresis time of the horizontal displacement of an arch dam is longer than that of a gravity dam.
concrete dam; displacement; hysteresis;temperature; analytic solution
中央高校基本科研业务费(B1020083)资助项目、国家自然科学基金重点项目(51139001)和河海大学水文水资源与水利工程科学国家重点实验室专项基金(20095860120)。

