基于可拓综合评价模型的隧道塌方概率计算方法

时惠黎，马淑芝，贾洪彪

（中国地质大学（武汉）工程学院，湖北 武汉 430074）

伴随着中国基础设施建设进入快速发展时期，隧道工程也如雨后春笋般蓬勃发展，各种隧道的设计和施工技术也有了长足的进步［1］。但在我国隧道建设取得巨大成就的背后，由于地质环境复杂、基础信息不充分和施工技术复杂等［2］，导致塌方、突涌、大变形和岩爆等灾害事故频发，使隧道工程成为一项高风险工程。在各类隧道灾害中，塌方又是最为常见的，也是影响隧道安全施工首要灾害，不仅给隧道施工带来巨大困难，且延误工期、耗费资金，并造成不良的社会影响［3］。因此，对隧道稳定性进行评价具有现实意义。

隧道稳定性受地质因素和工程因素的综合影响，具有随机性、模糊性、可变性等不确定性的特点，目前难以对隧道发生塌方的概率做出准确评估。鉴于此，本文以杉溪隧道为例，在深入研究各种风险评价方法的基础上，引进可拓学理论并选取了一系列能反映隧道塌方概率的关键指标，在对指标量化分级后，建立了相应的物元模型，并采用层次分析法确定各评价指标的权重。这种将可拓学理论与层次分析法相结合，建立物元模型，对隧道塌方概率进行评估的方法，可为预测隧道塌方发生的可能性提供可靠的依据。

1 可拓综合评价法

可拓综合评价法［4-5］是基于物元理论的一种评价方法，该法适用于评价受多种因素影响的事物。其基本思想是把评价对象按评价目的划分成若干等级，由专家意见给出各等级物元的特征数据范围，再将评价对象的指标值代入各等级的物元中进行多指标评定，评定结果按它与各等级物元的综合关联度大小进行比较，综合关联度越大，就说明评价对象与该评价等级的符合程度越佳，即属于该等级。隧道塌方概率可拓综合评价法的步骤如下：

1.1 确定隧道塌方概率的经典域和节域

根据物元理论，可以将经典域物元定义如下：

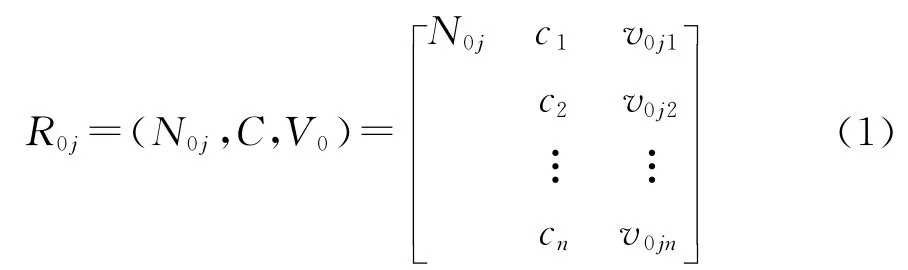
式中：R0j为隧道塌方概率的经典域物元；N0j为第j个评价等级；ci为 第i 个评价指标；v0ji=〈a0ji，b0ji〉为N0j关于指标ci所取的量值范围，即各等级关于对应的评价指标所取的数据范围经典域，i=1，2，…，n。

类似于经典域，节域物元可以表示为

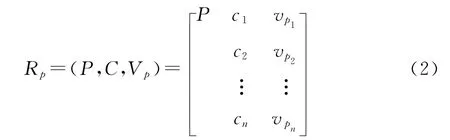
式中：RP为隧道塌方概率的节域物元；P 为各指标的全体评价等级的数值范围；vpi=〈api，bpi〉为P 关于指标ci所取的量值范围，即P 的节域。

1.2 确定待评物元

对于待评隧道p，将所收集到的数据信息和分析结果用物元表示，即可得到待评物元R：

式中：vi为待评隧道p 关于指标ci的量值，即从待评隧道收集到的各参评指标的实际数据。

1.3 确定各评价指标关于隧道塌方概率等级的关联度

各单项评价指标关于隧道塌方概率等级j的关联度为

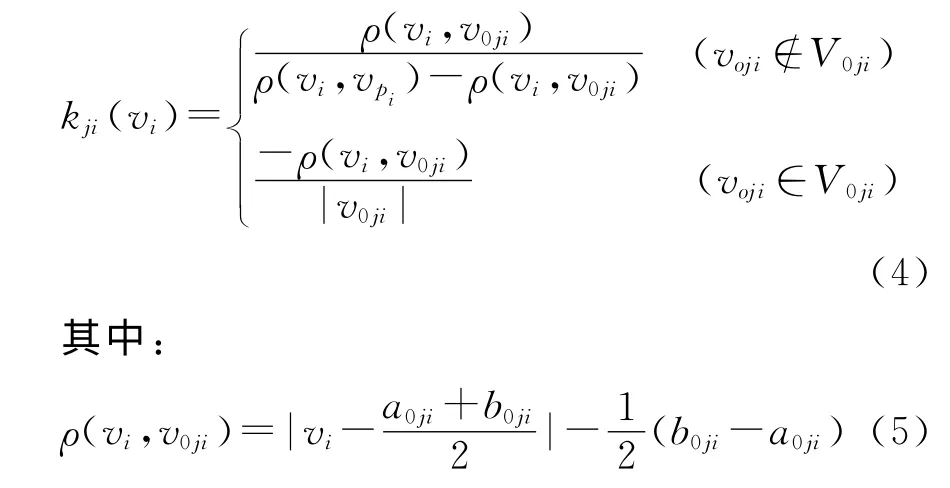
式中：vi为待评价物元的量值；kji（vi）为待评价事物的评价指标i关于评价等级j 的关联度；v0ji为经典域物元的量值范围；vpi为节域物元的量值范围；ρ（vi，v0ji）为点vi与有限区间v0ji的距离；ρ（vi，vpi）为点vi与有限区间vpi的距离。

1.4 计算待评隧道关于塌方概率各评价等级的关联度

待评隧道关于评价等级j的关联度为

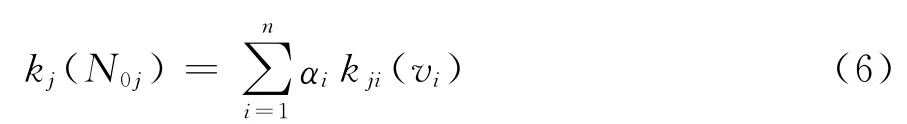
式中：αi为各评价指标的权重。

1.5 判定隧道塌方概率等级

待评隧道塌方概率等级为

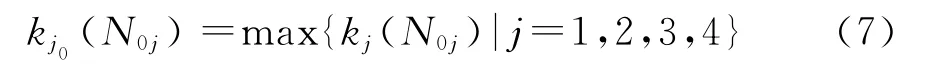
由式（7）则可定性判定待评隧道p 属于j0类。

2 隧道塌方概率计算方法

2.1 指标选取及量化分级标准

由于隧道塌方的影响因素较多，因此此次评价指标的选取遵循以下基本原则：选择能针对隧道具体的地质条件，全面反映隧道稳定性的参数；选择能通过现场勘查或室内外试验获得的定量或半定量数据指标。在对现场掌子面开挖、隧道塌方实例研究的基础上，选取了以下6个指标作为分类依据［6-9］。

（1）岩石坚硬程度σci。以岩石单轴饱和抗压强度σci进行等级划分，该指标是衡量岩体质量的一个重要指标，能反映岩块的软硬程度及岩性特征。地下硐室开挖前，围岩处于稳定状态，而隧道开挖后，破坏了原有的应力平衡，硐室的围岩需进行应力重分布。理论计算结果表明，岩石强度越低，围岩重分布应力影响范围越大，围岩越容易失稳。

（2）岩石完整性KV。岩体完整性系数KV是影响隧道工程稳定性的一个重要因素，该参数能反映地质构造及岩体结构特征。在开挖地下硐室时，同样强度的岩石，在重分布应力影响下，随围岩的完整性降低，重分布应力影响范围增大，围岩的稳定性降低。

（3）地下水流量Q。地下水流量Q 是诱发隧道塌方的最具活力和最具影响力的因素，该指标能反映岩体受地下水影响的程度。地下水对强风化和软弱围岩影响较大，尤其是沿线的云母石英片岩对水的敏感性极强。地下水能软化各类岩石，通过化学溶解或氧化还原作用使岩石强度降低，且不可忽视静水压力和动水压力的作用，在物理化学和力学的共同作用下，大大降低了围岩的自稳能力。

（4）隧道埋深H。隧道开挖后，隧道上方一定范围将形成相对稳定的自然承载拱，对隧道的稳定性有利，假若隧道上方覆盖层太薄，开挖的影响将波及地表从而不能形成承载拱，围岩自稳能力将大大下降，如果开挖后不及时支护或者支护强度不够，围岩就会发生塌方。因此，隧道埋深越浅，围岩自稳能力越差，塌方概率也就越高。

（5）隧道偏压θ。由于各种原因引起围岩的压力呈现明显的不对称而使支护结构受到偏压荷载，最终导致支护结构破坏而引起隧道塌方。引起隧道偏压的原因概括起来有：地形引起的偏移、地质构造引起的偏移、施工原因引起的偏移。为了简化分析，隧道偏压程度的划分主要考虑山体倾角，倾角越大，塌方的可能性就越大。

（6）施工效果L。施工效果一般包括施工单位技术水平和管理水平。就目前国内隧道施工状况而言，施工单位较多，各公路隧道施工队伍的技术水平参差不齐，不规范施工的现象较为普遍，主要体现在施工方法选择不当、支护强度不够、防排水措施不力、开挖进尺不当、支护背后有空洞、施工进度安排不合理等，这些问题都对隧道的塌方起到不可忽略的诱发作用。

根据隧道塌方的特征和《铁路隧道风险评估与管理暂行规定》［10］，本文对隧道塌方概率等级分为4级，各指标的分级标准见表1。

表1 隧道塌方概率各指标分类标准Table 1 Classification standards for tunnel collapse probability indexes

2.2 隧道塌方概率计算的物元模型

本文将隧道塌方概率等级分为4级：N01为不太可能，N02为偶然，N03为可能，N04为很可能，在已建立的塌方概率指标及其量化分级标准基础上，可将塌方概率各等级的经典域物元表示为

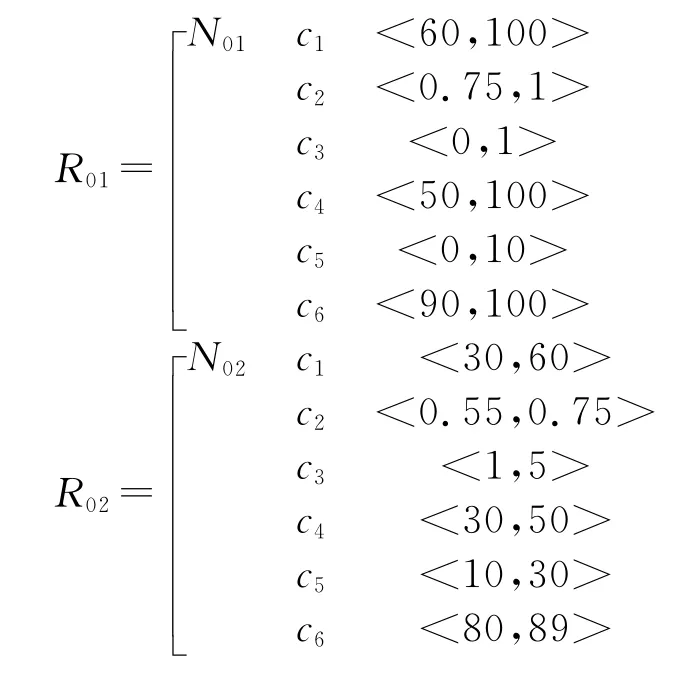
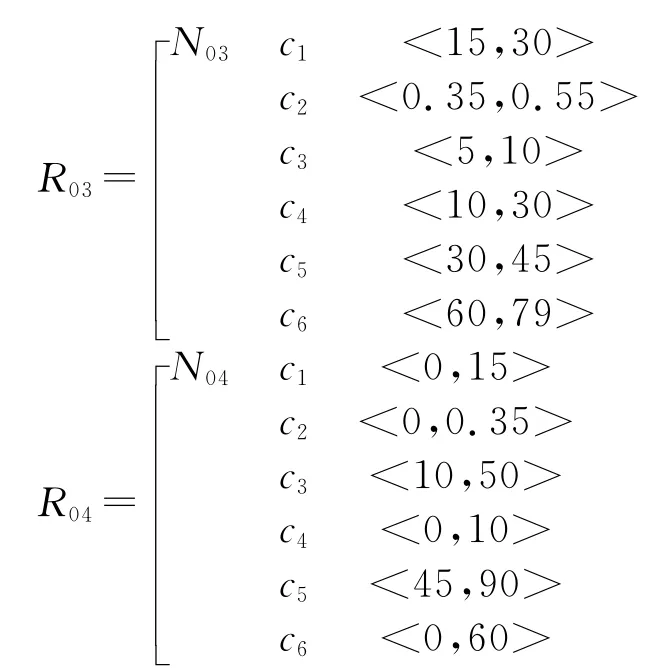
隧道塌方概率的节域物元为

3 工程应用

3.1 工程背景

福建京台线的杉溪隧道是处于剥蚀丘陵地区的分离式隧道，隧道左线起止里程为ZK27+378～ZK27+565，左洞长为187m；隧道右线起止里程为YK27+580～YK27+802，右洞长为222 m。隧道最大埋深约53 m，相对高差为10～56 m，埋深较小，洞线短，地质条件复杂，区域地质构造作用强烈，地下水不发育。根据钻孔资料揭露的地质情况看，岩层大多为风化的云母石英片岩，沿线围岩风化程度变化较小（见图1）。本次研究选取具有代表性的典型岩段（左洞掌子面ZK27+445）作为试验段，计算隧道该岩段的塌方概率。

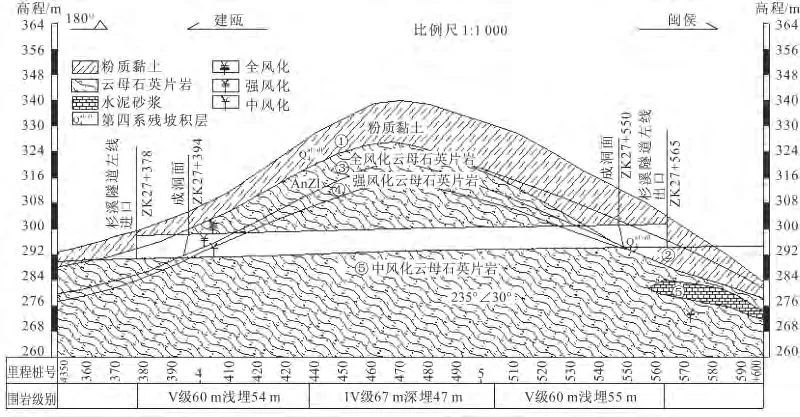
图1 杉溪隧道剖面图Fig.1 Shanxi tunnel profile

3.2 待评价物元的选取

本断面岩性主要为强风化云母石英片岩，围岩级别为V 级，岩石完整性差，岩性软弱，根据室内试验，确定岩石的饱和单轴抗压强度σci=9～15 MPa；根据统计掌子面的岩体单位体积裂隙系数JV=22条／m3，可判定岩体为破碎等级［11］，岩体完整性系数KV=0.15～0.35；通过现场地质调查，掌子面水量极少，仅局部地段偶有滴水，滴水量在0～1 L／（min·m）；从隧道剖面图（见图1）可知，里程ZK27+445断面的埋深为38m；现场实测的边坡角度为49°；根据现场实际情况，施工效果整体较好，应评为良好（80～89分）。

综合以上分析，可得到待评物元为

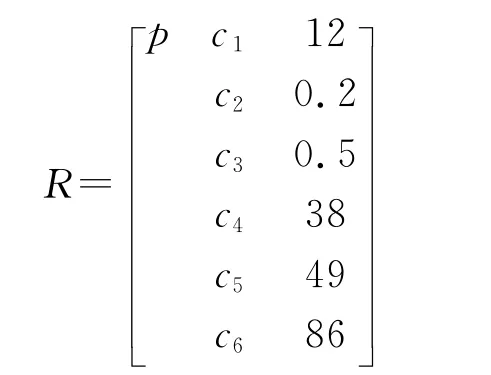
3.3 采用层次分析法确定评价指标的权重

（1）通过对相关专家和设计施工人员的调查与咨询，统计出各个影响因素的两两比较矩阵，见表2。

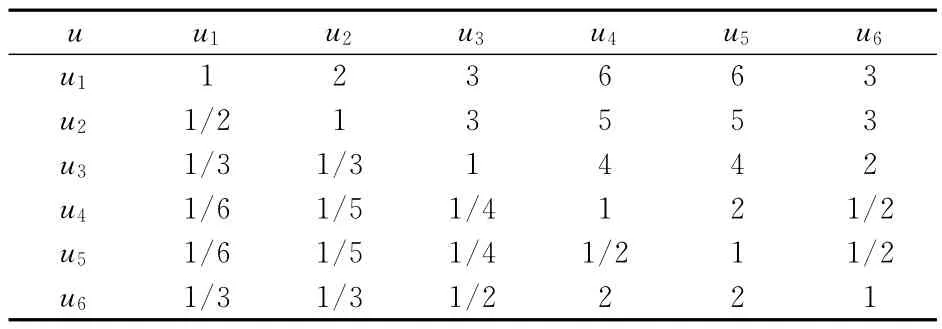
表2 ZK27+445段隧道塌方评价因素两两比较矩阵Table 2 Pairwise comparison matrix of evaluation factors indexes of tunnel collapse at ZK27+445section

（2）采用方根法求出上述判断矩阵的最大特征根λmax=6.194 3，并对其对应的特征向量归一化，得到评价指标的权重集α=（0.370，0.276，0.155，0.057，0.045，0.098）。

（3）进行一致性检验［12］。一致性指标CI为

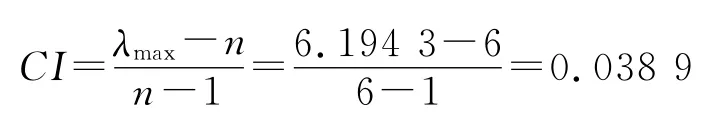
随机一致性指标RI为

RI=1.24

一致性比率CR 为

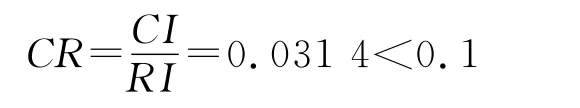
其结果通过一致性检验，确定的权重集α 即为所求的各评价因素的权重。

3.4 计算待评物元的关联度

根据式（4），可计算出待评隧道塌方概率等级的关联度矩阵为

根据式（6），可计算出待评隧道塌方概率等级的综合关联度，见表3。

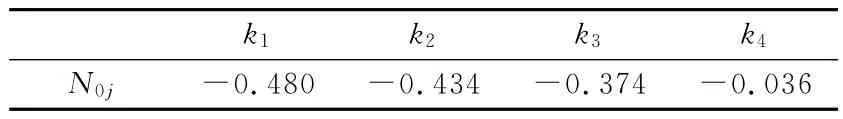
根据前述的评价规则，由式（7）可得

maxkj（N0j）=k4（N0j）=-0.036（j0=4）

3.5 评价结果分析

通过将利用层次分析法计算出的隧道塌方各评价指标的权重进行比较可知，各评价指标对隧道塌方影响程度的相对大小为：σci＞KV＞Q＞L＞H＞θ。根据强风化云母石英片岩段隧道塌方概率等级关联度计算结果，隧道塌方的最大关联度为-0.036，按评定标准可确定本次选取的左洞掌子面ZK27+445处隧道塌方概率为很可能（j0=4）。根据现场施工情况，该处已经发生了塌方（见图2），其得到的结果与现实情况相符合。

图2 左洞掌子面ZK27+445处塌方Fig.2 Collapse at the tunnel face ZK27+445of left hole

4 结论

可拓学方法从多角度、多因素出发，所选取的参数种类和数量均不受限制，可以适用不同隧道工程的具体特点，且将定性评价和定量评价相结合，形式简单，方便易行。本文基于可拓学理论并结合层次分析法，确定了隧道塌方概率的经典域和节域以及关联度的计算方法，构建了一个新的隧道塌方概率评估的物元模型。通过对杉溪隧道塌方概率的可拓学分析表明：可拓综合评价模型用于计算隧道塌方概率是合理的、可行的，能够较全面地反映多因素对隧洞稳定性的影响，满足工程实践的需要，对塌方的预测有一定的指导意义，为今后隧道塌方评估提供了一条新的思路和有效途径，同时也开拓了可拓学的应用领域。

［1］周宗青，李术才，李利平，等.浅埋隧道塌方地质灾害成因及风险控制［J］.岩土力学，2013，34（5）：1375-1382.

［2］王华牢，李宁，王皓.隧道施工塌方风险评估与控制措施［J］.交通运输工程学报，2010，10（4）：34-38.

［3］周建昆，吴坚.岩石公路隧道塌方风险事故树分析［J］.地下空间与工程学报，2008，4（6）：991-998.

［4］蔡文.物元模型及其应用［M］.北京：科学技术出版社，1994.

［5］陈巨龙.从物元分析到可拓学［M］.北京：科学技术文献出版社，1996.

［6］袁龙.基于模糊层次综合评估法的隧道洞口段塌方风险评估［D］.西安：长安大学，2010.

［7］苏永华，刘科伟，张进华.基于粗糙集重心理论的公路隧道塌方风险分析［J］.湖南大学学报（自然科学版）2013，40（1）：21-26.

［8］陈洁金，周峰，阳军生，等.山岭隧道塌方风险模糊层次分析［J］.岩土力学，2009，30（8）：2365-2370.

［9］安永林，彭立敏，吴波，等.隧道坍方突发性事件风险可拓法综合评估［J］.中南大学学报（自然科学版），2011，42（2）：514-520.

［10］中华人民共和国铁道部.铁建设［2007］200号铁路隧道风险评估与管理暂行规定［S］.北京：中国铁道出版社，2007.

［11］刘佑荣，唐辉明.岩体力学［M］.武汉：中国地质大学出版社，2006：22-26.

［12］许柏树.层次分析法原理［M］.天津：天津大学出版社，1988：28-30.

［13］黄小城，陈秋南，阳跃朋，等.可拓理论对复杂条件下岩溶隧道的风险评估［J］.地下空间与工程学报，2013，9（5）：1179-1185.

［14］许振浩，李术才，李利平，等.基于层次分析法的岩溶隧道突水突泥风险评估［J］.岩土力学，2011，32（6）：1757-1765.

［15］张勇慧，李红旭，盛谦，等.基于模糊综合评判的公路岩质边坡稳定性分级研究［J］.岩土力学，2010，31（10）：3151-3156.

［16］任洋，李天斌，熊国斌，等.基于可拓理论的高地应力隧道围岩分级法及应用［J］.工程地质学报，2012，20（1）：66-73.