泡沫铝百叶窗声屏障隔声计算及验证

周 强，何 宾，伏 蓉，张春岩，肖新标

(1.四川正升声学科技有限公司，成都 611130；2.西南交通大学 牵引动力国家重点实验室，成都 610031)

泡沫铝百叶窗声屏障隔声计算及验证

周 强1，何 宾2，伏 蓉2，张春岩2，肖新标2

(1.四川正升声学科技有限公司，成都 611130；2.西南交通大学 牵引动力国家重点实验室，成都 610031)

基于3D有限元法和隔声计算理论，将百叶窗叶片考虑成多孔吸声材料，建立开孔声屏障声学有限元隔声计算模型，并基于此模型分析泡沫铝材料属性对百叶窗声屏障隔声性能的影响。隔声计算模型通过现有理论与试验结果对比验证，理论验证不考虑泡沫铝材料，试验对比验证考虑泡沫铝材料。基于验证后的有限元隔声计算模型，调查泡沫铝材料流阻率和降噪系数对百叶窗声屏障隔声性能的影响。结果表明，声屏障计权隔声量与泡沫铝流阻率近似为线性关系，并且泡沫铝材料流阻率越小越好；声屏障计权隔声量与泡沫铝降噪系数呈指数关系，当降噪系数大于0.55时，进一步提高吸声材料的降噪系数对百叶窗声屏障隔声量影响较小。

声学；声屏障；降噪系数；计算模型；流阻率

百叶窗结构通常用于密封建筑开孔处，起到保护室内隐私和通风的作用，在巴西和其他热带国家百叶窗结构还用于减小室内的太阳辐射[1]。消声百叶窗结构主要用于需要同时满足通风和减小噪声的设备外侧，在传播途径上减小噪声。目前高速铁路声屏障主要为金属插板式直立声屏障，因为其较高的隔声性能得到广泛的应用。但在列车脉动风力作用下，H型钢立柱会出现螺栓松动及声屏障结构产出疲劳破坏现象。根据韩珈琪[2]研究结果，百叶窗声屏障可以减小27%的气动载荷，能有效减小H型钢立柱所受弯矩力。百叶窗声屏障安装于铁路两侧，用于减小列车运行噪声对周围环境的影响，并降低声屏障受到的气动载荷，延长使用寿命。

Lyons[1]对百叶窗声屏障厂家调查结果显示，德国、美国、英国厂家主要根据ISO 140评价百叶窗声屏障的隔声性能，但ISO 140需要在隔声室测试，成本较高，生产厂家很少对声屏障隔声性能进行优化。因此，有必要提出高效率准确的百叶窗声屏障隔声性能预测模型。Elvira[3]对百叶窗声屏障传递损失测试方法进行研究，将测试结果与使用低频Babinet[4]理论和高频衍射理论计算结果对比；G.R. Watts[5]简化模型，采用二维边界元方法研究了不同倾角百叶窗的隔声性能，且计算耗时较长。范丽丽[6]对公路泡沫铝声屏障现场降噪效果进行了测试。对于开孔声屏障隔声，3D有限元计算模型计算能调查不同结构和材料的隔声，并且具有成本低，计算时间短的优势。

本文通过3D有限元计算模型获得了纯抗性百叶窗声屏障和泡沫铝声屏障的隔声曲线，分别与抗性声屏障理论值和基于ISO 140测试得到的隔声量对比验证。最后根据验证得到的计算模型分析泡沫吸声材料流阻率和降噪系数对百叶窗声屏障隔声量的影响。

1 百叶窗声屏障隔声计算理论

计算模型基于平面波传播理论，忽略泡沫铝声屏障单元板结构振动的影响，考虑为多孔吸声材料，最后计算得到百叶窗声屏障的隔声量。

1.1 声学有限元法隔声量计算

有限元法可以用来计算复杂结构由施加激励函数引起的响应。声屏障用于减小一个方向上辐射的直达声场。对于具有足够大面密度的无孔屏障，到达接收者的声音强弱将和绕过屏障边界的衍射现象密切相关。而百叶窗声屏障属于开孔声屏障，声音由通过声屏障孔隙、声源到场点的直达声和绕过声屏障边界的衍射组成，声屏障隔声性能直接影响降噪性能。根据隔声计算理论的定义，百叶窗声屏障隔声量为入口面声功率与出口面声功率比值。公式1为百叶窗屏障隔声计算公式，在三维有限元计算过程中，假设出口和入口面积相等，入口处定义质点振动速度为1 m/s，并且设置出口面为无反射条件。隔声量计算公式可表示为[7,8]

1.2 多孔吸声材料特性

多孔吸声材料含有大量的微孔和缝隙。材料较薄时，吸声性能主要由黏滞损失和其表面密度决定。厚度接近或超过波长，声波在其中传播的距离较长，需要考虑空气豁滞性和热传导作用。多孔性材料的固体骨骼在空气声中一般当作硬骨骼。空气的声阻抗率很小，通常假设骨骼不随之振动。所以，讨论空气中的多孔性材料时，只讨论空气在材料中传播。下面通过Allard[8]多孔吸声材料传播模型，建立多孔材料属性与吸声系数关系。多孔材料的动态密度和动态弹性模量计算公式分别为[9]

式中 μ是空气的黏度，α∞为结构因子，ℓ为特征长度[10]；γ是比热容比，P0是大气压强，NPr是空气普朗特数，是空气比热容，κ是热导率。

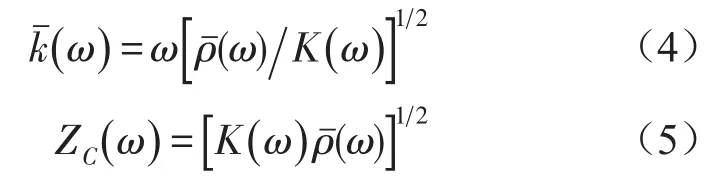
将多孔吸声材料背面装在坚硬表面上，L表示材料的厚度，其表面上声阻抗率Z可以表示为

因此，具有刚性背面多孔吸声材料的吸声系数可以表示为

2 隔声计算模型及验证

2.1 隔声计算模型

为了与混响室隔声测试结果进行验证分析，以泡沫铝百叶窗声屏障样件为实体模型，建立计算模型。如图1所示，其中泡沫铝材料孔隙率为84%，体积密度为440 kg/m3；泡沫铝单元板厚度为9 mm，长度为152 mm，单元板间声腔厚度为13 mm。

在设置百叶窗声屏障隔声3D有限元计算模型过程中，单元板间的间隙和入口出口设置为声腔，忽略单元板振动的影响，只考虑泡沫铝材料的吸声性能，因此简化为采用Allard模型估计的多孔吸声材料。根据试验样件大小和计算机硬件水平，在隔声计算模型中3D声学网格设置为985 mm×172 mm×100 mm，其余尺寸与百叶窗声屏障隔声测试样件一致。

在抗性百叶窗声屏障计算模型中，数值模拟边界条件具体为：

图1 百叶声屏障安装于隔声室洞口照片

（1）出口面设置为无反射边界条件，即空气特征阻抗为ρc≈416.5 kg/m2·s；

（2）声腔网格中除了出口面，其余面设置为刚性面；

（3）假设空气初始流速为0 m/s。在泡沫铝百叶窗声屏障有限元计算模型中，还需要设置声腔网格与泡沫铝材料网格接触面耦合，即泡沫铝材料与声屏障网格表面声压连续。

在计算模型中，泡沫铝材料的材料参数直接影响到声屏障的隔声性能。韩宝坤[11]提出影响金属材料吸声性能的主要参数有孔隙率、流阻率和结构因子。孔隙率为材料内部孔隙所占体积百分比，流阻率可近似等于材料两边的压强差与空气流经材料的线速度之比，结构因子是材料表面与孔隙毛细管夹角有关的物理量。泡沫铝结构因子[12]α∞≈2，由于泡沫铝微孔直径较大，需要根据Carai[13]试验得到的公式（8），计算得到材料的流阻率

式中ρm为材料的体积密度，A=25.989，B=1.404。因此声屏障样件所用泡沫铝材料R≈315 000 Pa·s/m2。

2.2 抗性百叶窗声屏障计算模型验证

片式消声器由大量消声通道组成，一个消声单元的消声性能代表着整个片式消声器的性能。因此，结构类似的泡沫铝声屏障可等效为一个消声单元，如图2（a）所示。对于纯抗性百叶窗声屏障，泡沫铝不具有吸声特征[14]，消声单元的传递损失主要为变截面处噪声的衰减，声波在此种变截面的传播过程与单扩张室消声器类似[13]，因此可等效为单扩张室。如图2（b）中消声器的尺寸，等效为图2（a）中噪声入口尺寸a1、通道宽度b1和进出口面距离L1。

图2 刚性百叶窗单元等效为单扩张室

图3为纯抗性百叶窗声屏障计算值与理论值对比，其中理论值曲线是根据扩张室理论公式得到，纯抗性百叶窗声屏障有限元计算只考虑声腔网格，与泡沫铝接触表面设置为刚性。以理论值曲线为标准，从图中可以看出，采用有限元法计算得到的抗性百叶窗声屏障频率隔声曲线与抗性单扩张理论计算得到的隔声曲线具有一致的频谱变化规律，都是随着频率周期变化。仅在隔声量峰值处，有限元计算结果比理论值大1.0 dB左右。可能是由于抗性百叶窗声屏障单元板与声源的入射角及出口面成45o，附加一部分传递损失。

图3 纯抗性声屏障有限元计算与理论值对比

2.3 泡沫铝百叶窗声屏障模型验证

使用泡沫铝百叶窗声屏障预测模型，根据公式（1），得到其隔声曲线，并且与纯抗性百叶窗声屏障对比，如图4所示。抗性声屏障吻合谷在1 000 Hz，泡沫铝声屏障最大吻合谷频率为800 Hz，相对而言吻合谷频率变小；在泡沫铝声屏障吻合谷频率以上，泡沫铝声屏障隔声性能明显优于抗性声屏障，并且随着频率的增大，隔声量也不断的增加；而吻合谷频率以下，泡沫铝声屏障略微低于抗性声屏障。对以上三种条现象，在李军[11]对汽车圆管泡沫铝消声器实验测试结果中有相同特征。因此，泡沫铝声屏障预测隔声曲线可真实反映声屏障样件的隔声性能。

根据ISO 140-3隔声测试标准，将图1中声屏障样件在隔声室中测试获得其隔声量，并且与泡沫铝声屏障计算结果对比，如图5所示。可以看出仿真与测试隔声量曲线吻合得较好，其中测试计权隔声量RW=8.6 dB，预测计权隔声量RW=7.4 dB，计算误差在可接受误差范围。1 000 Hz中心频率以下测试隔声量比仿真计算值大5 dB以内。Elvira[3]提到百叶窗声屏障在1 000 Hz以下频率，由于受声室和发声室会出现声强耦合，ISO 140-3测试隔声量会比真实值大2 dB～5 dB。在1 000 Hz以上，测试与仿真结果吻合较好，误差在3 dB以内。因此，仿真隔声量曲线合理，并且预测隔声量和隔声室测试结果吻合较好。

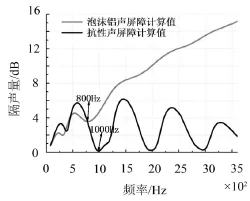
图4 抗性与泡沫铝声屏障隔声曲线

图5 隔声试验与仿真结果对比

3 泡沫铝材料对隔声量影响

对于几何结构相同的泡沫铝百叶窗声屏障，隔声量影响因素主要有孔隙率、厚度、结构因子、吸声系数和流阻率。本节通过仿真分析，调查流阻率及吸声系数对声屏障隔声量的影响。

3.1 流阻率

材料流阻率越接近空气特性阻抗（约ρc≈416.5 kg/m2·s），吸声系数则越高，反之，若材料的流阻率过大或过小都使得材料的吸声性能较差。根据公式（8）可知，泡沫铝材料流阻率与面密度成指数增长关系。现在市场上所提供泡沫铝材料流阻率通常在105以上，此时流阻越大其吸声性能较差。通过预测泡沫铝流阻率为105～5×10 Pa·s/m2。百叶窗声屏障隔声量，分析流阻率与隔声量的关系。模型中结构因子设置为2，孔隙率为0.84。

图6为流阻率与声屏障计权隔声量关系，由于拟合函数的1阶导数在-1～0的范围以内，计权隔声量与泡沫铝流阻率可近似为线性关系，因此，泡沫铝材料流阻率尽量选择较小。图7为不同流阻率预测的隔声曲面，从图中可以看出，在500 Hz频率以下，流阻率增加，百叶窗声屏障隔声量基本不变。流阻率从10增加到50，隔声量仅降低0.5 dB。这是由于泡沫铝材料低频噪声绕射能力强且吸声性能较弱造成。从吻合谷800 Hz到1 250 Hz频率处，随着流阻率增大，隔声量显对数变化，即当流阻率增加到2 ×105以上时，隔声量减小值在1 dB以内；1 600 Hz频率以上，除较大流阻率以外，隔声量随着流阻率增加而线性减小，同时1 600 Hz以上频率隔声量较大，主导了计权隔声量的变化趋势。

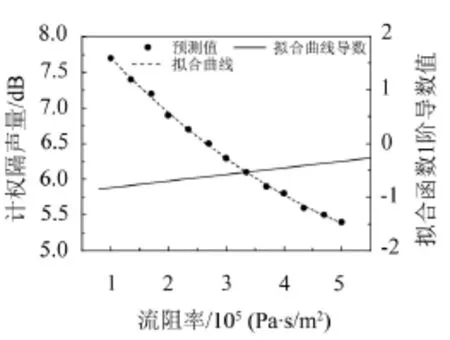
图6 流阻率与计权隔声量曲线

图7 不同流阻率泡沫铝声屏障隔声曲面

3.2 吸声系数

吸声系数对百叶窗声屏障隔声量影响分析中考虑了表1的计算工况，其中孔隙率采用现有泡沫铝材料参数设置，结构因子根据孔隙率大小[13]确定，流阻率采用公式（7）计算得到；降噪系数先根据Allard理论计算不同材料的吸声系数，进而求得250 Hz、500 Hz、1 000 Hz和2 000 Hz吸声系数平均值，即降噪系数。

表1 不同吸声系数计算工况

公式（8）为降噪系数与计权隔声量拟合关系式，其中权隔声量与泡沫铝降噪系数为指数，拟合函数残差值达到0.02。图8为降噪系数与计权隔声量拟合曲线，当降噪系数大于0.55，拟合曲线1阶导数值较小，计权隔声量曲线较平稳，当降噪系数大于0.55时，进一步提高吸声材料的降噪系数对百叶窗声屏障隔声量影响较小。

式中x为降噪系数。

图9为不同降噪系数预测声屏障隔声曲面，从图中可以看出：在500 Hz频率以下，隔声量随着降噪系数增加而降低0.5 dB以下，主要原因是泡沫铝材料低频吸声性能较弱；从吻合谷800 Hz到1 250 Hz频率处，随着降噪系数增大，隔声量线性减小；1 600 Hz中心频率以上，随着吸声系数增大，隔声量呈指数规律减小，降噪系数在0.55以上，其隔声量减小量在1 dB以内，同时由于1 600 Hz以上频率隔声量较大，主导了计权隔声量的变化趋势。

图8 降噪系数与计权隔声量曲线

图9 不同吸声系数泡沫铝声屏障隔声曲面

4 结语

文中通过理论和试验验证了百叶窗声屏障隔声量预测模型，应用验证后的模型对流阻率和减噪系数参数进行分析，可以得到以下结论：

（1）纯刚性百叶窗声屏障隔声量可用声学有限元计算，也可等效为单扩张室消声器的传递损失理论值；

（2）预测模型中加入泡沫铝材料时，百叶窗声屏障隔声吻合谷频率由1 000 Hz平移到800 Hz。吻合谷频率以上，隔声性能优于纯抗性声屏障，并且随着频率的增大，隔声量也不断的增加；吻合谷频率以下，隔声量低于纯抗性声屏障1 dB以下；

（3）泡沫铝百叶窗声屏障隔声测试计权隔声量RW=8.6 dB，预测计权隔声量RW=7.4 dB，1 000 Hz各1/3倍频程中心频率以下，测试隔声量比仿真计算值大5 dB以下，在隔声室对低隔声量样件测试的误差范围以内；

（4）泡沫铝材料流阻率越小越好，其中1 250 Hz以上频率隔声量较大，并且与泡沫铝流阻率为线性关系，导致声屏障计权隔声量与泡沫铝流阻率也近似为线性关系；

（5）计权隔声量与泡沫铝降噪系数呈指数关系，当降噪系数大于0.55时比较合理。500 Hz频率以下，隔声量受降噪系数影响较小；在中频段，随着降噪系数增大，隔声量线性减小；1 600 Hz以上频率隔声量较大，主导了计权隔声量的变化趋势。

综上所述，在选择泡沫铝声屏障材料时，泡沫铝流阻率选择越小越好，降噪系数为0.55最为合适。文中有限元预测模型为声屏障隔声计算提供了一种方法，可进一步对不同几何参数声屏障隔声性能进行研究。

[1]Lyons R.Building elements of low sound insertion loss [D].University of Liverpool,1993.

[2]韩珈琪.高速铁路声屏障结构特性研究及减载式声屏障技术初探[D].成都：西南交通大学,2014.

[3]Elvira.Evaluation of the acoustical performance of louvre by impulse response analysis[D].University of Liverpool. 1998.

[4]Cremer L and Müller H.Principles and Applications of Room Acoustics[J]. Applied Science Publishers，1982,(2):181-190.

[5]G.R.Watts.Measured and predicted acoustic performance of vertically louvred noise barriers[J].Applied Acoustics. 2001,62:1287-1311.

[6]范丽丽，泡沫铝声屏障降噪效果测试与机理研究[D].东北大学，2009.

[7]林好利，陈传举.基于有限元法的抗性消声器声学性能分析[J].内燃机与动力装置，2007，101(5)：20-24.

[8]曹玉煌，罗马吉.不同截面布置的抗性消声器三维声学性能分析[J].噪声与振动控制，2010，30(3)：153-155.

[9]Allard J F,Champoux Y.New empirical equations for sound propagation in rigid frame fibrous materials[J]. Acoust SocAm.1992,91:3346-53.

[10]Chao-nan Wang,Jiunn-hwan Torng.Experimental study of the absorption characteristics of some porous fibrous materials[J].AppliedAcoustics.2001,62:447-459.

[11]李玉娟.泡沫铝复合结构传递损失分析[J].噪声与振动控制，2011，31(6)：116-118.

[12]李军.圆管泡沫铝消声器性能分析与实验研究[D].山东科技大学，2008.

[13]Massimo Garai,Francesco Pompoli.A simple empirical model of polyester fibre materials for acoustical applications[J].AppliedAcoustics,2005,66:1383-1398.

[14]方丹群.噪声控制工程学[M].北京：科学出版社，2013：576-717.

Calculation and Verification of Sound Insulation of FoamAluminum Louver Sound-barrier

ZHOU Qiang,HE Bin,FU Rong,ZHANG Chun-yan,XIAO Xin-biao
(1.Sichuan ZisenAcoustics Technical Co.Ltd.,Chengdu 611130,China; 2.State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China)

A 3D finite element model(FEM)of a louver sound barrier for sound insulation analysis was established. This model was verified by comparing the computation output with the result of testing.Considering that the louver was made of foamed aluminum.The influences of the flow resistance and the noise reduction coefficient of the foamed aluminum on the sound insulation of the louver sound barrier were investigated.The results show that the weighted sound insulation and the aluminum foam flow resistance have a linear relationship approximately.And small flow resistance of the aluminum foam can yield good sound insulation effect.The weighted sound insulation and the noise reduction coefficient have an exponential relationship.When the noise reduction coefficient exceeds 0.55,further increasing of the noise reduction coefficient has small influence on the weighted sound insulation only.

acoustics;sound barriers;noise reduction coefficient;calculation model;flow resistance

U270.1+6；TU112.59+4

A

10.3969/j.issn.1006-1335.2015.03.011

1006-1355(2015)03-0046-05

2015－01－13

国家自然科学基金(U1434201)；国家863计划(2011AA11A103-4-2)

周强（1990－），男，四川自贡人，硕士研究生，目前从事高速列车振动与噪声研究。E-mail:18108270132@163.com

肖新标，男，副教授，硕士生导师。E-mail:xiao@home.swjtu.edu.cn