简单问题复杂化
吴忠
我们在教学解决简单的实际问题时,发现最简单的实际问题一般由两个条件和一个问题所组成。它反映了实际生产、生活中的一个简单数量关系,也是构成复杂实际问题的“细胞”。在教学中,由于它太简单,有的教师认为“没有什么要教”而忽略过去,但是到教学解决复杂的实际问题题时,问题暴露出来了,很多学生连基本的数量关系都不甚清楚。所以,我们必须从低年级开始就要启发和引导学生逐步掌握分析、解决简单实际问题时的思路,简单的问题其实也可以复杂化。下面谈几点做法。
一、图形结合,重视理解实际问题的数量关系
儿童的思维处于以直观形象为主向抽象思维过渡的阶段,因此,图形结合是有效理解题意的最佳方法。教师可以让学生结合图例读题,启发和引导口述简单实际问题的已知条件和问题,让学生懂得简单的实际问题一般由两个条件和一个问题所组成,然后用自己的话来讲述其中包含的题意。
教学时首先教学例1,出示例题:草地上有1只母鸡,3只小鸡,一共有多少只鸡?教学中,可先出示1个大圆表示1只母鸡,再画出3个小圆表示3只小鸡,然后电脑显示画一个大圈,表示把两部分合并起来。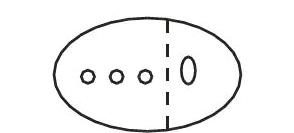
这样,用图和动作让学生理解求“一共”是多少,就是要我们把这两部分合并在一起。要求学生看着图用自己的话来复述题意:有两种鸡,一种母鸡,一种小鸡,大鸡有1只,小鸡有3只,要求一共有多少只鸡,就是问我们两种鸡合并起来,有多少只鸡。得出的隐含其内数量之间的关系:母鸡只数+小鸡只数=一共有鸡的只数。
接着教学例2:草地上有4只鸡,里面有3只是小鸡,其余的是母鸡,母鸡有多少只?教学时,可以利用上面的图让学生知道4只鸡里面有两种鸡:母鸡和小鸡;4只鸡中去掉3只小鸡,就是母鸡的只数。例2是例1的逆解题,这两个例题间的数量关系式通过同一幅图让学生领会。
二、简化思路,把实际问题转化成数学语言
教学上述例题后,接着问学生:为什么上面的图可以用大圆表示母鸡,用小圆表示小鸡呢?因为在教学里讨论的只是鸡的“只数”,只要大圆的个数1,小圆的个数3就行。所以,求一共多少只,只要求“1(只)和3(只)合起来是多少”就好了。这样,1、2两题即转化为:(1)1和3合起来是多少?(2)4去掉3还有多少?
例3:有5朵黄花,红花比黄花多3朵,红花有多少朵?
解题时,着眼于红花与黄花朵数的关系,解题思路可以化简为:“比5(朵)多3(朵)是多少朵?”这样便于学生学习。
最后,列出算式,计算,作答。
上述解决问题的逻辑过程是:简单的实际问题(分析数量关系)→数学语言文字题(根据运算意义)→数学算式题→计算→答案。
三、有机渗透,适当的简易方程思想
教学求一个数的几倍是多少的实际问题时,出示例4:少年宫歌咏组的人数是美术组人数的5倍。美术组有25人,歌咏组有多少人?
列式25×5=125(人)。
解答后,可以出示:
例5:少年宫歌咏组的人数是美术组的5倍。歌咏组有125人,美术组有多少人?
分析数量关系:“多少人的5倍是125人?”翻译成算式则为:?×5=125。
列出算式是125-5=25(人)。
这样,既沟通了解决乘除法实际问题的联系,又渗透了方程思想。
四、强化训练,领悟实际问题的结构
组织填写条件和补充问题的训练,填条件、补问题的训练,有利于学生生动地领悟简单实际问题的结构,发展他们的集中思维和发散思维。如下面的练习,还可以让学生从中得到美的感受: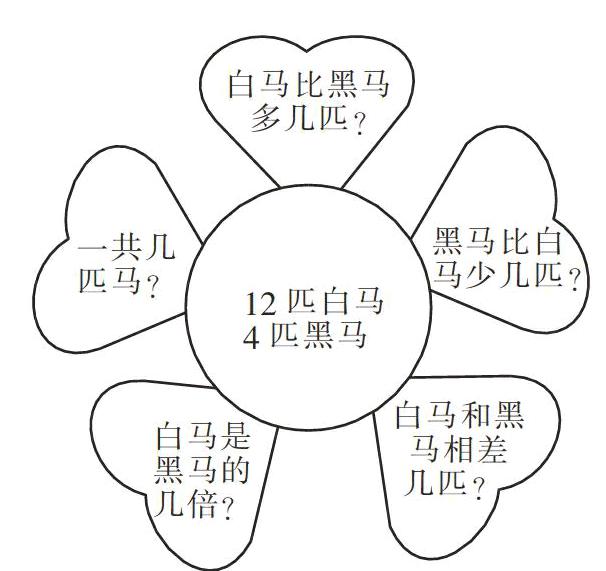
反过来,也可以出示一个问题和一个条件,如“12匹白马”与“白马比黑马多多少匹”,让学生填出另一个条件。
综上所述,简单实际问题的教学并不是简单的事,我们只有通过重视解决问题的启蒙教学,让学生理解实际问题中的数量关系;通过把实际问题转化成数学语言,通过渗透与强化训练,领悟实际问题的结构,发展他们的思维,提高他们解决问题的综合能力,为以后解决稍复杂的实际问题打好坚实的基础。

