舰船控制系统中复合误差控制算法

杜德银，杨代强

(重庆科创职业学院，重庆402160)

0 引 言

当今的舰船设计具有体积结构复杂、各种控制系统交互影响的特征［1］。船行驶与任务出动时，动力控制系统、电力推进系统、燃油控制系统及定位扫描系统相互工作会不可避免的造成系统误差，对舰船综合性能的控制产生不利影响;而且，舰船技术较为前沿，集机械、电力、电器、软件和弹道技术于一体，参数控制复杂，各控制系统带有误差性、非线性、不确定和混沌性特征，系统的偏差给舰船的综合性能控制造成困难，因此，复合控制系统的概念和解决方案应运而出。为了增强舰船的经济性、安全稳定性，协调好各系统，降低复合控制系统的综合误差便成为了一种有效的方法。因此，进行舰船复合误差研究也是现阶段舰船控制的一项重要课题。舰船控制系统复杂，多变量和随机性、非线性等复杂特征需要依靠现代控制理论和各种有效算法建立合适的研究模型，在研究模型的基础上，以多变量为参数，对控制过程的参数干扰误差多重反馈，保证最终获得理想的系统状态输出，提高舰船性能的稳定性和安全性。本文选取舰船电机控制系统中的滑动控制和神经网络控制为复合控制对象模型，并对控制模型控制过程进行复合误差算法研究，保证复合控制系统的输出稳定，提高舰船电机控制系统的综合性能。

1 误差特性

通常来说，误差就是输入量与输出量之间的偏差［2－3］。在不同的研究中又有着不同的分类，如时间序列误差、决策误差、学习控制误差等，误差的产生是由于控制过程中变量差参数受到干扰或系统内部性能下降造成的系统输出偏差。复合误差则是多变量系统综合作用误差的量化，由多个误差变量组成，常用于多输入多输出系统的分析中，通过建立输入输出模型，选取合适的符合误差算法，构建反馈过程，进行定性和定量分析，实现综合控制的平稳。

一般的控制系统是根据控制过程中误差变化与输出误差之间的间接特征关系，构造误差的特征向量进行误差整定的。假设在控制系统中初始时刻t0是某变量值为x(t0)，则根据数学导数公式知变量x(t)满足如下:

那么在控制过程中某个时刻t0，变量参数因扰动产生的误差可表达如下:

上述即是变量误差误差的推导公式，由公式知，变量误差随时间变化处于数值0 附近来回变化。因此误差可表示为描述变量变化的趋势特征，在控制系统中，往往希望变量值能符合期望要求，是变量误差保持在0 附近以控制误差对系统稳定造成的影响，若随变量x(t0)变化的控制函数定义为yd(t)，则控制误差有如下公式:

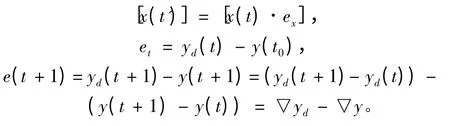
式中et为期望控制量值与实际期望值之间的误差，为了避免控制误差对控制系统的影响，通常引入虚拟误差ξ (t)和可控门限阈值进行补偿，如:

那么误差的特性可通过引入一组向量进行定量描述:

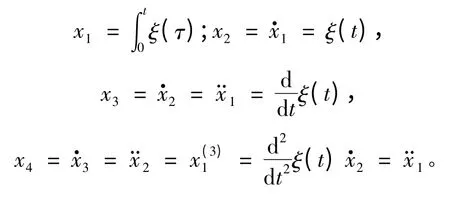
由x1，x2，x3，x4可组成误差特征的描述向量:

式中E 为误差的变化程度。控制系统能够进行有效的记忆和反馈补偿，根据系统的需要实时进行系统改善，保持系统的稳定特性。

2 复合误差控制算法及其模型

2.1 算法原理

舰船的所有控制系统都需要动力能量支持，大多舰船设备均使用电力机组来提供所需的能量，这样，势必增添电力装置的复杂性和在功率变换时的输入变量干扰，整个过程中多变量参数运行受到的干扰较为严重，过程遍布非线性和不确定特征。在复合控制中容易产生复合误差影响舰船的动力性能［4－5］。模糊神经网络算法能够根据变量参数，自学习、自调节、自整定的优点，专注于对变量参数偏差的提取和推理分析，获取过程经验，自动整定变量参数，合理控制。

因此，为了达到最大化的减小复合误差对电力控制系统的影响，本文选用模糊神经网络算法，利用其学习、自调节的算法特征，避免复合控制误差对系统性能稳定性造成影响。模糊神经网络算法模型通过对输入信号的加权和可微的正切函数之间的复合组成神经网络元函数进行以网络分层为模式自学习，不断深入理解系统控制目的。

在神经网络分层中，输入层为基础层;

式中xi为误差的积累、过程误差值大小及误差的变化状态特性和变化趋势。

第2 层:

其中:m和σ 分别为神经网络隶属的中心中心矢量和基宽向量;u 为记忆单元;θ 为记忆反馈。

第3 层:

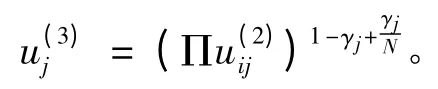
其中γ 为神经网络的自适应补偿量。

第4 层:

第5 层:

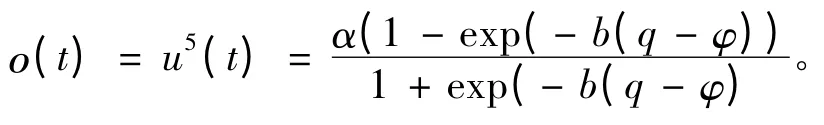
其中a，b，φ 均为系统的可调参数。

这样，通过各层对不同时刻系统输入参数的学习，可以捕捉系统的偏差动态变化行为，在自学习中，不断调整过程参数结构，以自适应的学习算法，优化系统过程，达到综合误差E 变化最小:

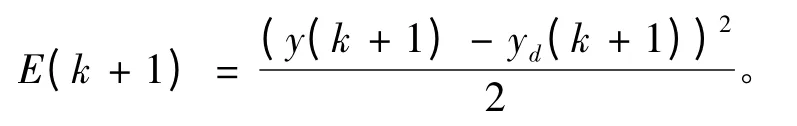
为了弥补上式的不足之处，需要进一步对第5层中的参数进行调整，令ρ=［a，b，φ］，则目标模型可表述为:

其中em(k)为模型的误差向量。在对误差进行采样学习时，常常引入卡尔曼滤波器，用去估计ρ，则模型公式转变为:

其中:

利用数学中的最速下降法，合理地整定出a，b，φ 参数的数值;

其中ξ 为最速下降法进行负梯度方向迭代计算时的迭代步长最小值。由a，b，φ的参数，实现对误差预期控制的误差向量最小变化的公式:

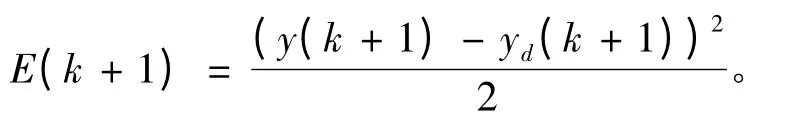
2.2 建立电机工作模型

电机工作由燃油装置提供能量来源，特别是舰船这种大型耗能设备，需要配置多组柴油发电机组进行多级控制实现多组电机工作。这样保证电机的转速，维护电机的电压和功率的稳定输出［6－7］。电机工作模型对分析电机控制系统工作性能很重要，电机在励磁恒定与电机组绕组对称下，定子电压方程、矩阵有如下表述:

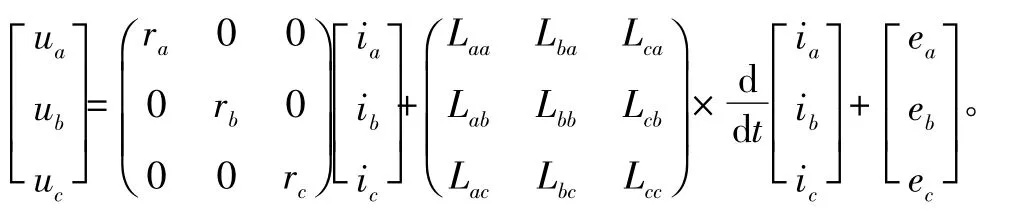
式中:ea，eb，ec为反动电势;ia，ib，ic为相电流公式。

转子动态方程为:

式中:θ，ωr，λf分别为电机的转角、转速和饱和系数;Te，TL，T0分别为电磁转矩、负载转矩和摩擦转矩。

这样，由上述公式可推导出电机的电磁转矩Te:

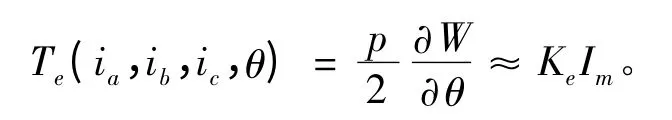
其中W和Im分别为电机的功率和控制电流。

这样经过一定的公式转换，对电机系统这样的多变量控制模型的研究就简化为了对电机转矩、转速和输出电流的分析上，为复合误差控制研究带来方便。

3 电机系统复合控制误差模型应用

在建立电机工作模型后，通过模糊神经网络算法进行电机复合误差控制研究就有了分析的变量参数和控制对象［8－9］。当变量参数的状态变化程度不大时，产生的状态变量误差会因为电机控制系统的设计被迫返回到正常的运行轨道，这种自觉的误差控制就通过滑动模块控制实现，利用滑动模块对变量扰动的快速响应，及时纠正误差偏离正常状态的趋势，达到预期的控制效果;同时，电机工作环境和系统复杂，需要自我纠正环境影响和参数变化对性能的不利影响，多重反馈，自学习、自调节，改正偏差，所以在电机控制中也需要模糊神经网络控制。本文将误差参数变量处于快速响应阶段的滑模控制和对偏差及时自学习、自调节的模糊神经网络控制有效结合，组成电机复合控制系统，按照电机工作模型，对复合的变量误差进行分析，在复合误差产生过程中进行科学控制，保证整个电机系统的稳定运行，提高舰船的综合性能。

3.1 电机的滑模控制研究

滑模控制具有非线性和不连续的控制特征，在系统动态下通过模块控制迫使状态按照预定的轨迹运行，操作简单，状态辨识容易。在电机中:

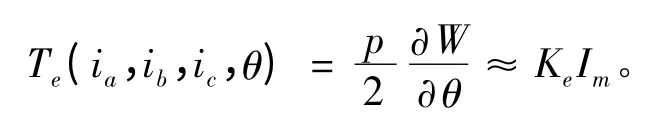
由上式可知，电机工作的最终输出为电流;而输入的则是转子速度误差和误差的状态变化量，速度状态的误差控制方程可描述为:

上述可分别表示出电机转子的速度误差eω和误差的状态变化量。那么在进行电机的滑动模块控制误差时，假设滑动模块状态S 满足:

则电机系统工作中，控制电流I*可转化为:

其中a，b 为控制增益。

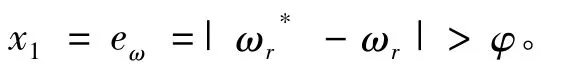
则电机进行滑模控制。

3.2 电机的模糊神经网络控制

电机的模糊神经网络控制即是通过模糊神经网络算法分层结构特性和自学习、自调节机制，对电机工作中的输入转速误差eω和转速误差的变化状态进行调节，实现输出电流变化参数ΔI*在合理的范围，维护电机控制系统的稳定。现令x1=eω，x2=;则模糊神经网络各层表示如下:

第1 层:

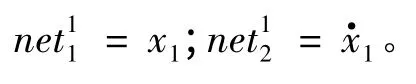
第2 层:

第3 层:

第4 层:

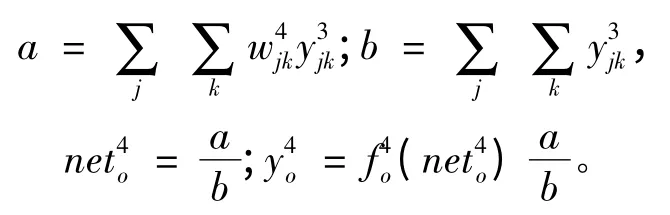
这样对电机输入中的转速参数进行控制时，根据神经网络分层学习，定义自学习的误差规则符合下式:

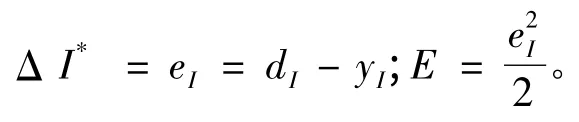
若E 满足工作要求，在电机转子速度误差超出φ的限制范围，即:

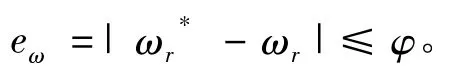
则可以利用自学习的模糊神经网络控制。

综上，从电机的滑动模态的控制和模糊神经网络控制可以看出，二者的控制目的在于电机系统的输出参数电流I*，但在任何时刻都只有一种控制发生作用。其复合控制的转子速度误差eω要求如下:

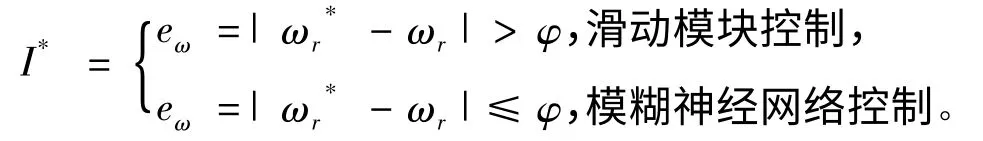
因此，电机复合误差控制即是对滑动模块和模糊神经网络的复合控制，根据系统状态变化，滑动模块和模糊神经网络模块进行暂态和稳态的交互响应，共同作用，保证电机的稳定运行。

4 仿真分析

对某舰船电力控制系统中电机复合控制的仿真分析，模拟仿真结果如图1所示，从结果可以看出，速度响应分为加速、减速和稳定3个阶段，在速度突然间改变时，速度加速或减速过程平稳有序，控制系统短时间内将转速调节恢复正常;在转速定常控制下时，即使增加负载，负载转矩突然改变，转速也按照设定进行运行;当电机的转速处于ω1的状态范围时，可以看到电流的输出I 同转矩T的变化相一致，在转速处于ω2和ω3的不断增大的范围状态下，电流I3和转矩T3的变化微小，说明转速的误差变化在电机的复合控制下对电流和转矩的影响较小，说明该复合误差控制算法对转速扰动的影响不敏感，并且电流I4随着转矩T4的增大而增大;在转矩处于T4并有一段的稳定状态时，转速ω4的减小反馈出了系统的输出电流的减少;在该复合控制系统中，电流的输出总是伴随着转速或转矩的变化趋势做出调整，最终实现电机系统功率的稳定调节，同时当转速在电机转速稳定时，电流随着转矩一起变化时并没有产生干扰抖动现象，增大电机速度也没有对电流和转矩发生严重影响。

图1 电机控制系统复合控制过程分析Fig.1 The analysis of composite control inmotor control system

该仿真结果证明了电机复合控制系统对复合误差扰动不敏感，复合控制具有抗干扰、自调节能力，保证了电机控制系统能在稳定、安全的模式下工作，具有环境自适应能力。

［1］陈子顺.船舶发电机励磁系统人工神经网络控制研究［D］.上海:上海海事大学，2004.

［2］李骥，张洪锁.用神经网络估计模型误差的预测滤波算法［J］.控制与决策，2005，20(2):183－186.

［3］李林欢，刘斌，苏宏业，等.基于输出误差预测的模糊预测PID控制及应用［J］.浙江大学学报(工学版)，2004，38(7):826－83.

［4］许荣彧，友文，华荣.基于PI－RP 复合控制策略的船用单相APF 设计与仿真［J］.舰船科学技术，2011，33(8):90－94.

［5］王稼祥，何信.误差补偿和时滞辨识预测控制算法［J］.电子科技大学学报，2005，34(6):817－20.

［6］徐杰，乔鸣忠，夏益辉.三相并联有源滤波器的新型复合控制方法［J］.舰船科学技术，2013，35(11):86－88.

［7］李高云.高海情下船舶减摇鳍智能控制系统研究［D］.哈尔滨:哈尔滨工程大学，2008.

［8］王雪丹，任继伟，张晓曦.复合控制算法在逆变器中的应用［J］.哈尔滨理工大学学报，2009，14(4):99－102.

［9］董丽荣，董文智.基于模糊－PID 复合控制算法的电机转速控制［J］.包头职业技术学院学报，2010，11(3):12－14.