桅杆雷达承载平台隐身性能分析

杜晓佳，崔俊伟，杨 飏，洪 明

(1.中国舰船研究设计中心，湖北 武汉430064;2.大连理工大学 运载工程与力学学部船舶工程学院，辽宁 大连116024)

1 概 述

雷达隐身性作为提高舰船生存能力的重要条件，可有效提升舰船在海战中的突防能力，是现代海战取胜的关键因素之一［1］。对于现代舰艇来说，雷达隐身技术是在一定评估区域内降低目标的可探测信号特征，即雷达反射截面积(Radar Cross Section，RCS)，从而减小被敌方发现的距离，降低其被识别和跟踪的概率［2-3］。自20 世纪80年代以来，国内外相继出现大量隐身舰艇，典型的隐身舰艇有法国“拉斐特”级护卫舰、中国054 型护卫舰、英国45 型防空驱逐舰和瑞典“斯米杰”号试验艇等。由于大量隐身技术被应用到这些隐身舰艇上，使得在海战中对其进行侦查和攻击变得十分困难。

桅杆系统一般处于水面舰艇结构的最高位置，且同时承载了舰上大部分的侦查和通讯设备，受地球表面弯曲效应的影响，它是舰船早期被雷达探测的主要散射源，因而桅杆系统为舰船雷达反射的重要部分，将直接影响到全舰的雷达隐身性能［4］。

图1 舰船雷达探测示意图Fig.1 The schematic of ship radar detect target

对舰艇桅杆外形进行隐身设计时，整个桅杆形体设计宜趋于封闭，减少凹凸面和垂直角，尽量避免有发生强散射的部件外露。但由于有关技术尚不成熟，在进行舰船桅杆的实际设计时，尚不能完全实现雷达天线的集成化。考虑电磁兼容问题，需将各雷达在桅杆表面分布设置，以致桅杆主体上存在大量的雷达承载平台，在桅杆表面形成众多较大的突出物。这些突出的雷达承载平台不仅有自身的电磁反射，还会与桅杆围板形成较大的二面角，进而可能产生较强的多重反射。因此在桅杆设计中，当完成桅杆主桅体的隐身设计工作后，有必要对其雷达承载平台的隐身性能进行计算和分析，并做出相应调整。

图2 桅杆的雷达承载平台示意图Fig.2 Radar platform of warship mast

快速多极子方法考虑了场点之间的相互作用，其计算结果包含了所谓传统高频算法中的多次散射作用。

本文以某一桅杆的雷达承载平台为例，基于快速多极子方法(FMM)和物理光学法(PO)2 种经典电磁散射计算方法，选取快速多极子作为电磁模型综合反射的计算方法，选取物理光学作为模型单次反射的计算方法。参照有关规范和文献，对其电磁散射方式进行分析，研究雷达波波长及极化方向的影响，分别分析该平台4个独立倾角的影响，给出具有较好隐身效果的平台外形参数。

2 电磁模型参数设定

雷达散射截面作为一个复杂的物理量，它既与被探测目标的几何参数和材料参数有关，又与雷达波的频率、极化方向和波形等参数有关，而且它还随目标相对于雷达波发射器或接收器之间的方位角变化而急剧变化［7］。

2.1 桅杆模型参数设定

考虑到电磁兼容的影响，雷达天线和桅杆主体的空间位置不发生变化，所以雷达天线及其与主桅体间的电磁反射不在本文的考虑范围内。因此在计算桅杆雷达承载平台的RCS 之前，需对该桅杆进行相应简化，只考虑部分桅杆围板对桅杆雷达承载平台雷达反射产生的影响。简化后的桅杆雷达承载平台模型如图3所示，其中桅杆主体围板高1.50 m，底部宽度为3.00 m，与竖直面倾斜7°，雷达平台外延长度为0.50 m，平台外端部宽度和高度均为0.20 m。

对平台的外形进行分析可知，平台外形可由图3所示的τ1，τ2，τ3和τ4四个独立倾角参数所控制。因此本文将以不同倾角的雷达平台模型作为对象进行隐身评估，分析这4个倾角对雷达平台隐身性能的影响。

图3 雷达承载平台外形参数Fig.3 Shape parameter of radar′sloaded platform

在进行桅杆雷达承载平台RCS 预估中，暂不考虑隐身涂层和FSS的影响，假设围壳材料为理想导体PEC。

2.2 雷达参数设定

对于舰船来说，威胁其安全的雷达波来自敌方水面舰船或空中武器平台，二者都接近水面，观察仰角被限制在一个极小的范围内［8］，如无特殊要求，一般雷达天线中心至舰艇水线部分连线与它的海平面投影之间的夹角不超过0.5°。因此本文的桅杆RCS 评估研究只针对沿水平面传播的雷达波展开。由于桅杆雷达承载平台模型沿纵剖面对称，在计算时水平方位角φ的范围只需选取0°～90°即可，本文的角采样间隔为1°，测量舷角以逆时针增量为正。

在海战中，作战舰船通常首先被敌方单个舰船或空中武器平台发现。因此对于舰船来讲，最重要的隐身特性指标就是其单站的RCS 分布，因此在本文桅杆隐身雷达研究工作中，只针对桅杆的单站RCS 进行研究。

对舰船进行探测的雷达多处于S，C，X和Ku波段，测量频段可在以上波段中选取，某一波段的实际测量中心频率一般可选该波段的中心频率，对应的波长分别为10 cm，5 cm，3 cm和2 cm。

此外，在对桅杆进行雷达散射截面计算时，考虑了极化方向对RCS的影响。

3 雷达承载平台散射方式分析

以τ1，τ2，τ3和τ4四个倾角均为0°的雷达平台为模型，分别利用快速多机子方法和物理光学法，计算其在波长分别为10 cm，5 cm，3 cm和2 cm 条件下，水平极化雷达波照射下的单站RCS，其RCS分布如图4所示。

从图4 可看出，在4个探测波长下，通过对比FMM和PO 计算得到综合反射和单次反射RCS 曲线对比可知，考虑多重反射后模型在评估区域内的RCS 值有较大提升，且多重反射影响的区域是比较广泛的，单次反射是评估域内RCS 峰值的主要来源。随着频率的增加，因单次反射的RCS 曲线差别较小。而计入多重反射后，RCS 曲线均有较大变化，且峰值有较大提高。

表1 为各波长下雷达承载平台的总雷达反射截面。

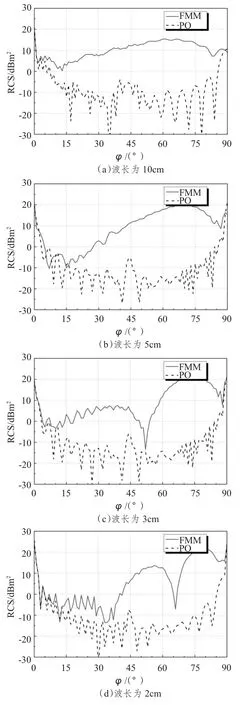
图4 不同波长下雷达承载平台RCS 分布Fig.4 RCS distribution of radar′s loaded platform in different wavelength

表1 总RCS 值对比Tab.1 Comparison of general value

同时也可看出，FMM法计算求得的计入多重反射效果的目标总RCS 值与PO法求得的单次反射总RCS 有较大差别。因此对于以τ1，τ2，τ3和τ4四个倾角均为0°的雷达承载平台模型来说，多重反射是其电磁反射的主要反射源。且雷达波长越小，该目标的总雷达截面积就越大。

随后，依然以τ1，τ2，τ3和τ4均为0°的雷达平台为模型，分别利用快速多机子方法和物理光学法，计算在波长为10 cm 不同极化方向雷达波照射下，在评估区内单站RCS的平均值，结果如图5所示。可以看出，随极化角度的改变，物理光学法计算出的单次反射RCS的平均值并不发生改变，而FMM 计算得到的模型整体RCS 分布的平均值有略微的改变，但这种改变基本可以忽略。因此极化角度对该模型的单次反射和多重反射的影响均是较小的，基本可以忽略。

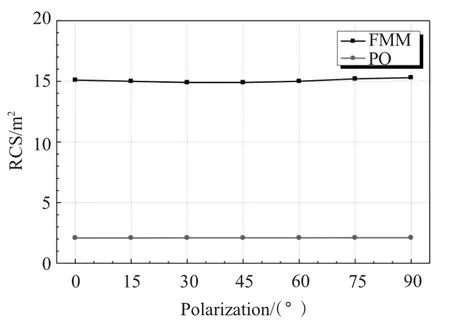
图5 不同极化方向下雷达平台RCS 平均值Fig.5 RCS average of radar platform in different polarization direction

4 雷达承载平台隐身性能分析

针对雷达承载平台进行外形调整，降低其雷达反射值，修改平台的围板倾角是较为简单和直接的方法。鉴于桅杆及雷达平台围板均为内倾设计，为保证满足电磁兼容和强度，雷达平台外延长度、外端部宽度和高度保持不变。因此本文将以不同倾角的雷达平台模型作为对象进行隐身评估，分析这4个倾角对雷达平台隐身性能的影响。

当τ1，τ2，τ3和τ4四个倾角中任一倾角从0°增加到15°时，其余3个倾角均为0°。在波长为10 cm水平极化雷达波照射下，通过快速多极子方法，对雷达承载平台在评估区的RCS 平均值和总雷达反射截面进行计算，其变化如图6～图9所示。

单独考虑τ1的影响。随着τ1的增加，雷达平台在评估区域内的平均值和总RCS 值仅有微小改变，略有提升，可见夹角τ1对评估域内的RCS的影响较小，2 条曲线最后趋于相同，说明特征方向±4.5°内的测量值相对于其它区域较弱。

图6 RCS 随τ1 分布曲线Fig.6 The distribute curve of RCS changedwithτ1

单独考虑τ2的影响。随着τ2的增加，雷达平台在评估区域内的平均值和总RCS 值呈现出线性的增加，即τ2越大，评估域内的RCS 整体水平就越大，2 条曲线保持的差距是相同的，因此特征方向±4.5°内的测量值对这种变化影响较小。当τ2增加时，基座两侧的面积就越大，即二面角效应就越大，因而导致在非特征方向±4.5°内RCS的增加。

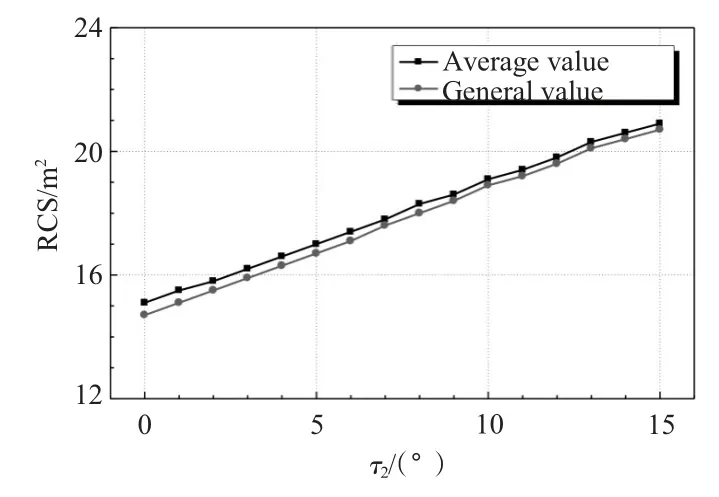
图7 RCS 随τ2 分布曲线Fig.7 The distribute curve of RCS changedwithτ2

随着τ3的增加，在2°～8°之间，雷达平台在评估区域内的平均值和总RCS 值呈现出明显的降低，但当τ2增大到一定程度时，2 条曲线的降低趋势就变得比较缓慢，且2 条曲线间的差距趋于增大，可见特征方向±4.5°内的测量值相对其它区域较高。

图8 RCS 随τ3 分布曲线Fig.8 The distribute curve of RCS changedwith τ3

随着τ4的增加，当小于10°时，雷达平台在评估区域内的平均值和总RCS 值呈现出明显的线性降低。当τ2大于10°后，评估域内的RCS 整体水平随τ2的降低就变的相对缓慢;当τ2大于13°后，平台的RCS 水平反而随τ2的增大而增大。2 条曲线保持的差距随τ2的增大一直增大，可见特征方向±4.5°内的测量值在RCS 平均值的影响就越大。

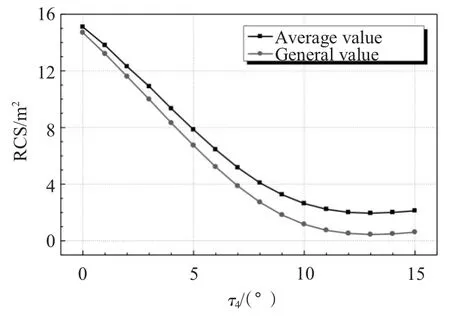
图9 RCS 随τ4 分布曲线Fig.9 The distribute curve of RCS changedwith τ4

为研究4个倾角对雷达承载平台RCS的综合影响，对τ1，τ2，τ3和τ4四个倾角共同从0°增加到15°的16个模型进行研究，在波长为10 cm 水平极化雷达波照射下，雷达承载平台在评估区的平均RCS 值和总RCS 变化如图10所示。

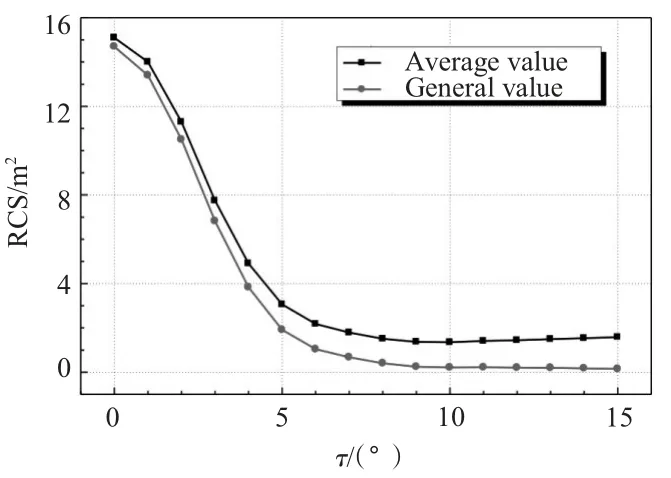
图10 雷达承载平台RCS 随倾角τ 分布曲线Fig.10 The distribute curve of radar′s loaded platform RCS changedwith τ

随着4个倾角的共同增加，当小于8°时，雷达平台在评估区域内的平均值和总RCS 值呈现出明显的降低;当倾角大于10°后，评估域内的平均值和总RCS 值随倾角的变化相对缓慢，但此时评估域内的平台的RCS 平均值随倾角的增大有略微的增大。2 条曲线保持的差距随倾角的增大一直增大，可见特征方向±4.5°内的测量值在RCS 平均值的影响就越大。

综合雷达平台平均值和总RCS 值随倾角变化规律，单独考虑4个倾角参数时，τ3和τ4这2个倾角对雷达平台的隐身性能影响较大，τ1对雷达平台隐身性能的影响较为有限，τ2的增加反而降低模型的隐身性能。当综合考虑4个参数时，当雷达平台4个倾角共同大于5°时，即可得到相对满意的隐身效果。在16个相同倾角模型中，当4个倾角均为10°时，评估域内的平均值为全局最优，且总RCS 值处于局部最优，建议作为最终设计结果。

5 结 语

本文以某一桅杆的雷达承载平台为例，基于快速多极子方法和物理光学法2 种电磁计算方法，对其电磁散射方式进行分析，讨论了雷达波参数和外形参数的影响，具体结论如下:

1)对于该平台原始模型，多重反射是其电磁反射的最主要源，且多重反射影响的区域是比较广泛的，单次反射是评估域内RCS 峰值的主要来源。

2)当雷达波长越小，该目标的总雷达截面积就越大。频率的改变对多次反射的影响要大于对单次反射的影响。雷达波的极化角度对该模型的单次反射和多重反射的影响均较小。

3)综合雷达平台平均值和总RCS 值随倾角变化曲线，2个平台侧面的倾角τ3和τ4对雷达平台的隐身性能影响较大，端面倾角τ1对雷达平台隐身性能的影响较为有限，底面倾角τ2的增加会降低模型的隐身性能。综合考虑4个参数的影响，当雷达平台4个倾角均为10°时，评估域内的平均值为全局最优，且总RCS值处于局部最优，可获得相对较好的隐身效果。

［1］吕明云，黄敏杰，武哲.封闭式隐身桅杆的初步设计与效果评估［J］.电波科学学报，2010，25(5):833-838.

［2］阮颖铮.雷达截面与隐身技术［M］.北京:国防工业出版社，1998.

［3］林忆宁.21 世纪水面战舰设计的新攻略-隐身性和战斗力兼优［J］.船舶工程，2004，26(5):1-7.

［4］杨德庆，常少游.舰艇外形雷达隐身设计特征面法［J］.中国造船，2008，49(2):113-119.

［5］黄培康，殷红成，许小剑.雷达目标特性［M］.北京:电子工业出版社，2005.

［6］CRISPIN J W.Methods of radar cross-section analysis［M］.New York:Academic Press，1968.

［7］程子君，吴启华.隐身桅杆与主船体耦合RCS 特性研究［J］.中国舰船研究，2011，6(3):45-48.

［8］张考，马东立.军用飞机生存力与隐身设计［M］.北京:国防工业出版社，2002.