一种Apriori改进算法在2型糖尿病危险因素分析中的应用

韦 哲,叶广健

（1.兰州军区兰州总医院，甘肃兰州，730050；2.兰州理工大学电信学院，甘肃兰州,730050）

一种Apriori改进算法在2型糖尿病危险因素分析中的应用

韦 哲1,2,叶广健2

（1.兰州军区兰州总医院，甘肃兰州，730050；2.兰州理工大学电信学院，甘肃兰州,730050）

目的：为了提高Apriori算法在2型糖尿病相关危险因素分析中的执行效率。方法：2型糖尿病患者的信息来自兰州某三甲医院医学信息科，包括2009年1月至2014年3月的2型糖尿病患者的首次病程记录及其健康数据档案。在研究前人对Apriori算法改进的基础上，并根据2型糖尿病相关危险因素分析中的需要，提出了一种适用于2型糖尿病相关危险因素分析的Apriori算法改进办法。最后用C#语言对这两种算法进行编程，对它们的执行效率做了分析。结果：得到了这两种算法在频繁项集与支持度、运行时间与记录数、运行时间与支持度这三个方面的对比图。结论：这种改进Apriori算法在2型糖尿病相关危险因素的分析中更有执行效率。

数据挖掘；Apriori算法；关联规则；算法改进

0 引言

糖尿病（Diabetes Mellitus）是由胰岛素分泌缺陷和（或）胰岛素作用缺陷所引起的，并以慢性高血糖伴碳水化合物、脂肪和蛋白质的代谢障碍为特征的慢性疾病。2型糖尿病（Type 2 Diabetes Mellitus）主要由胰岛素抵抗伴随相对胰岛素分泌不足，或胰岛素分泌缺陷伴有或不伴有胰岛素抵抗而产生，占糖尿病的90%～95%。近年来随着世界各国社会经济发展和居民生活水平的提高，生活方式的改变和人口老龄化，糖尿病患病率在世界范围内呈上升趋势，已成为最常见的慢性非传染性疾病之一。预计到2030年全球成人糖尿病总人数将从2000年的1.71亿增长到3.66亿，增长1.14倍。因此，对2型糖尿病的研究具有重要的意义。

本课题小组在挖掘2型糖尿病相关危险因素之间关联规则时发现，由于Apriori算法自身的缺陷：①每生成一个频繁项集就必须扫描一次数据库；②由（k-1）频繁项集生成k项候选项集时，会产生许许多多的候选项集，而这些候选项集很多以后是用不到的，使得2型糖尿病相关危险因素的数据挖掘等待时间较长，执行效率较低。针对2型糖尿病相关危险因素关联规则挖掘数据量大，数据属性值众多等特点，并结合前人对Apriori算法的改进方法，本文提出了一种适用于2型糖尿病相关危险因素关联分析的Apriori算法。

1 建立挖掘规则

1.1 Apriori算法

Apriori算法是一种逐层搜索迭代用法，用k项集搜索（k+1）项集。首先对数据库进行扫描，统计每一个项的计数，找出大于等于最小支持度的项集，构成频繁1项集的集合，记为L1。然后，在L1中搜索频繁2项集，记为L2，再找L3，如下循环下去，直到不能再找到频繁项集为止。每一次寻找Lk都要扫描一次数据库。如前所述，Apriori算法挖掘规则的过程分两步来实现：

a.找到所有频繁项集L。

b.从频繁项集L中提取强关联规则。

第1步是Apriori算法的关键所在，是决定此算法性能是否优良的评价关键，第2步相对简单。目前，Apriori算法改进方法大多也是针对第1步。其主要步骤发现频繁项集过程又分为两步：连接步和剪枝步。

(1)连接步：为了找到频繁项集合Lk，需要连接Lk-1与自己产生连接候选项集k-项集的集合。该候选频繁项项集合记作Ck。设l1和l2是Lk中的项集。记li[j]表示li的第j项。执行连接过程Lk-1Lk-1，其中要求Lk-1的元素 l1和l2可以连接的，如果：（l1[1]= l2[1]）（l1[2]=l2[2]）…（l1[k-2]=l2[k-2]）（l1[k-1] l2[k-1]），连接l1和l2产生的结果项集是l1[1]，l1[2]……l1[k-1]，l1[k-1]。记号li[j]表示li的第j项。

(2)剪枝步：扫描数据库，确定Ck中每个候选集的支持度计数。但是，候选集Ck可能很大，为压缩Ck，可以利用以上算法性质：任何非频繁项集合的（k-1）-项集都不可能是频繁项集合k-项集的子集。所以，如果一个候选k-项集的（k-1）项子集不在Lk-1中，则该候选也不可能是频繁的，因此，从Ck中删去。

Apriori算法自1994年被R.Agrawal等人提出来以后，在数据挖掘领域得到了广泛的应用，但是作为第一个关联规则算法和最经典的关联规则算法，Apriori算法有其自身的缺点：1)每次生成频繁项集需要扫描一次数据库；2)生成许多没有价值的候选项集。

针对以上两个缺点，前人提出了很多改进的办法。文献[4]提出了基于分片的方法，它的主要改进思路是对于所要求的事务数据库进行两次扫描。文献[5]提出了一个效率高的能够生成频繁集的方法，基于杂凑(Hash)的算法。通过实验我们能够发现，寻找频繁项集的主要工作就是生成频繁2项集的时候，引入杂凑的技术来对频繁2项集的产生进行了改进。文献[6]提出了基于采样的方法，它是基于之前一次扫描事务数据库时得到的数据，对它进行了详细的组合以及分析，从中我们可以得到一个改进的办法，其基本思想是：先采用从事事务数据库中抽取出来的采样，得到某些在整个事务数据库中的一些规则，其中这些规则是可能成立的，然后我们用事务数据库中剩余的部分去验证这个规则是否在整个事务库中都成立。

2 一种适用于2型糖尿病相关危险因素关联分析的Apriori算法

本课题小组在对2型糖尿病相关危险因素进行数据挖掘的时，从兰州某三甲医院医学信息科提取了3万余份2型糖尿病患者的首次病程记录及健康数据档案。选取了15个相关危险因素，分别为：性别、年龄、文化程度、身体质量指数(BMI)、腰臀比(WHR)、性格、创伤史、饮酒、饮茶、吸烟、睡眠、运动、收入水平、职业、按时三餐。在对这些原始数据进行数据预处理时，我们采取了如下的办法：以身体质量指数为例，身体质量指数这一项，绝大多数数据都集中在[23，30]之间，可采用等分法划分以下区间：（0，23]，[24，25]，[26，27]，[28，29]，[30，+]，这5个区间分别对应数字1、2、3、4、5，则BMI这一项可以转化成如下形式，（0，23]，[24，25]，[26，27]，[28，29]，[30，+]分别对应于B1、B2、B3、B4、B5。最后将这选定的15个相关危险因素转化为44个属性值，3万多个数据44个属性值，如果采用经典Apriori算法，这个计算量是巨大的，会消很多电脑I/O开销，并且耗时巨大。对此，本文提出了一种适用于2型糖尿病相关危险因素关联分析的Apriori算法。

2.1 理论基础

在对其算法进行改进之前，我们需要了解几个Apriori算法的相关性质，这能有助于我们更好的对算法进行改进。

性质1：非频繁项集的超集就一定是非频繁项集。

性质2：频繁项集的所有非空子集都是频繁项集。

性质3：存在一个事物集I， 已知I有着k频繁项集Lk，如果k频繁项集Lk可以生成k+1项频繁集Lk+1，那么必然有着k频繁项集中项集的个数大于k[7]。

2.2 改进方法

2.2.1 扫描数据库的改进

扫描数据库的改进主要是针对经典Apriori算法在生成频繁项的过程中，每生成一次频繁项集就必须对数据库进行一次扫描，将大于等于最小支持度阈值的项集保留，将小于最小支持度阈值的项集剔除这个缺陷。显然反复扫描数据库将消耗大量的时间和电脑内存，如果我们减少扫描数据库的次数，算法的效率将会大大提高。具体的改进办法如下：

首先，我们需要建立一个二维数组A[m][n]。我们需要对整个事务数据库的所有项进行统计并排序，使得这些数据有着一定的顺序，排序完后对整个事务数据库进行扫描，对于每个事务里包含的项，我们用1来表示，对于不包含的项，我们用0来表示。然后我们将这些数据都存入之前创建的二维数组当中。存入后，我们再分别求出二维数组里的每列包含1的项的和，得出的结果是1项集的频繁度。我们再将它与最小支持度进行比较，如果大于或等于最小支持度，那就是频繁项集，如果小于最小支持度，那就不是频繁项集，将其删除。

2.2.2 剪枝步的改进

我们把性质3的思想应用于剪枝步的改进。在经典A即priori算法中运用的是性质2进行剪枝处理，非频繁项集的超集就一定是非频繁的，但是应用这样方法处理完后，生成的候选项集中还是会存在许多冗余的频繁项集，这样没有减少计算量。我们现在应用性质3的方法，先计算|Lk-1(n)|，如果其中存在|Lk-1(n)|k-1的元素，那么就将包含有这些元素的项集删除，得到一个新的频繁项集，再与自身连接，得到此时的候选项集的结合。

2.2.3 布尔矩阵的改进

矩阵的改进也同样采用了性质3的思想。已知一个候选k项集，我们需要对矩阵进行扫描，来得到k频繁项集，我们在扫描的同时，对矩阵进行压缩。也就是说我们在计算支持度时，与每列中含有“1”的个数进行对比，如果包含“1”的个数小于或是等于k时，那么我们就将这一行从数组中删除，等之后再次进行扫描时，我们就无需扫描该行，从而达到了将事务库进行了缩减，减少了算法扫描数据库所用的时间，提高了算法的效率。

2.3 算法描述

输入：交易数据库D，最小支持度阈值min_sup

输出：可以产生规则的所有频繁项集L

(1)Initalzing Arrary(D,A[m][n+1]);

(2)L1=find_frequent_1_itemset(A[m][n]);

(3) for(k=2;Lk-1;k++)｛

(4) Ck=apriori_gen(Lk-1,min_sup);

(5) for each cCk;

(6) for(i=1,in;i++)

(7) if(A[i][C[1]])(A[i][C[2]])…(A[i] [C[k]]

(8) c.count++;

(9)｝

(10)Lk=｛cCk|c.countmin_sup｝;

(11)return L=UkLk

3 实验结果

为了证实改进的Apriori算法的性能，用C 语言对这两种

图1 频繁项集与支持度的关系

图2 运行时间与记录数的关系

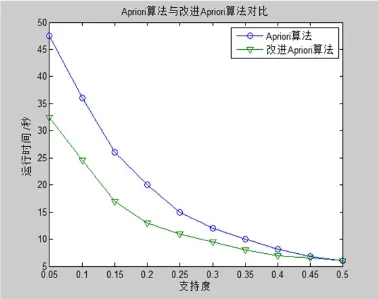
图3 运行时间与支持度的关系

算法进行编程，并用这两种模型分别对预处理后的2型糖尿病相关危险因素初始集进行数据挖掘，实验硬件条件为CPU为Intel i5处理器，内存为4G，操作系统为WIN 8系统。分别从频繁项集与支持度、运行时间与记录数、运行时间与支持度这三个方面进行考量。实验结果如下图1至图3所示。

[1] Wild S,Roglic G,et al.Global prevalence of diabetes-Estimates for the year 2000 and projections for 2030[J].Diabetes Care,2004,27(5):1047-1053.

[2] 黄晓霞,萧蕴诗.数据挖掘应用研究及展望[J].计算机辅助工程, 2001: 23-29.

[3] 邵峰晶,于忠清.数据挖掘原理与算法[M].科学出版社, 2009,8:1-2.

[4] Purnami.A new expert system for diabetes disease diagnosis using modified spline smoothsupportvector machine[J].Computational Science and Its Applications,2010,3:83-92.

[5] Rakesh Agrawa,Jerry Kiernan.Water marking Relation Databases.Proceeding of the 28th VLDB Conference,Hong Kong,China,2002.

[6] R.Agrawal,T.Imielinski and A.Swami.Mining association rules between sets of items in large databases[A].In Proc.of the ACM SIGMOD Intl Conf. on Mangagement of Data[C].

[7] 邵峰晶,于忠清.数据挖掘原理与算法[M].北京:中国水利水电出版社,2003

One Apriori Algorithm in the Application of Analyzing Risk Factors of Type 2 Diabetes

Wei Zhe1,2,Ye Guangjian2
(1.Lanzhou General Hospital,Lanzhou Military Area Command, Gansu ,Lanzhou 730050,China；2. School of Electrical Engineering and Information Engineering,Lanzhou University of Technology, Gansu, Lanzhou，730050,China)

Purpose:We do it to improve the efficiency of analyzing risk factors of type 2 diabetes. Method: We use the patients’ data from the information department of one tertiary referral hospital in Lanzhou which include course note of disease and their health record form January 2009 to March 2014.We find out one improved algorithm applies to analyze risk factors of type 2 diabetes based on original Apriori algorithm and it’s requirement.And we analyze the efficiency by programming both of the algorithms with C# .Result: We can analyze the chart of frequent item and support degree,time and number of records,time and support degree. Conclusion: This new improved Apriori algorithm has a high efficiency in analyzing risk factors of type 2 diabetes.

Data mining;Apriori algorithm;Association rules;Algorithm improve