复杂路网交通信号协同控制的优化研究

何玮梁坤

(1.新疆农业大学机械交通学院,新疆乌鲁木齐 830000;2.天津科技大学机械工程学院,天津 300457)

复杂路网交通信号协同控制的优化研究

何玮1梁坤2

(1.新疆农业大学机械交通学院,新疆乌鲁木齐 830000;2.天津科技大学机械工程学院,天津 300457)

目前,城市交通拥堵问题已严重影响了城镇居民生活,制约了城市的经济发展。对城市道路交叉口信号配时提出了更高要求.结合乌鲁木齐市交通拥堵的现状,根据乌市道路平面交叉口与信号配时的特点,提出了以延误、排队和通行能力三个指标进行信号协同控制优化的问题,并建立了基于流量大小、排队和绿信比大小的信号优化模型。结合实际路口分析对模型进行了验证,证明了该模型和算法的有效性。

复杂路网 协同控制 信号优化模型

目前，城市交通拥堵问题已严重影响了乌鲁木齐市城镇居民生活，制约了城市的经济发展，研究一种经济合理、环保节能、协调有效的解决城市交通拥堵问题的的方法，成为人们关注的焦点。在综合比较分析并参考国内外经验[1][2]的基础上，城市道路交叉口信号配时优化，将是解决交通拥堵问题的一个很好的方法。但是，不同的城市有它特殊性，需要考虑城市本身的路网交通特征。

本文结合乌鲁木齐市交通现状，借鉴国内外现有交通信号控制配时设计的研究和应用成果[3][4][5]，依托目前使用的信号机，对乌市交叉口信号配时设计方法进行研究，提出一套适合乌鲁木齐交通现状的信号配时设计方法。

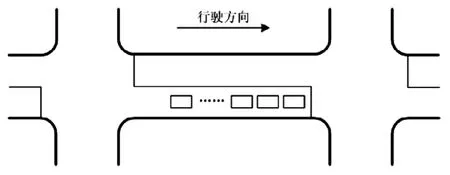
图1 车队头部受阻的情形

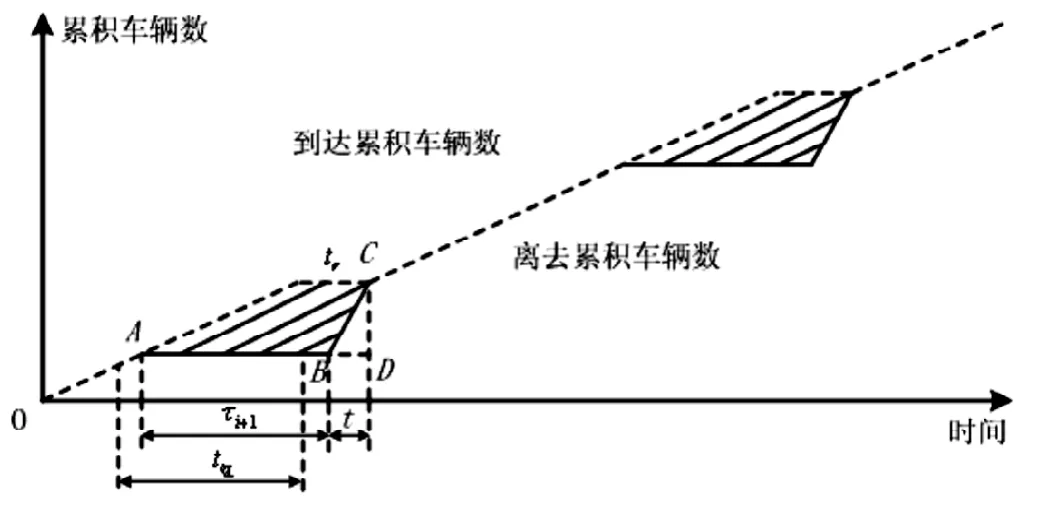
图2 车队头部受阻延误示意图

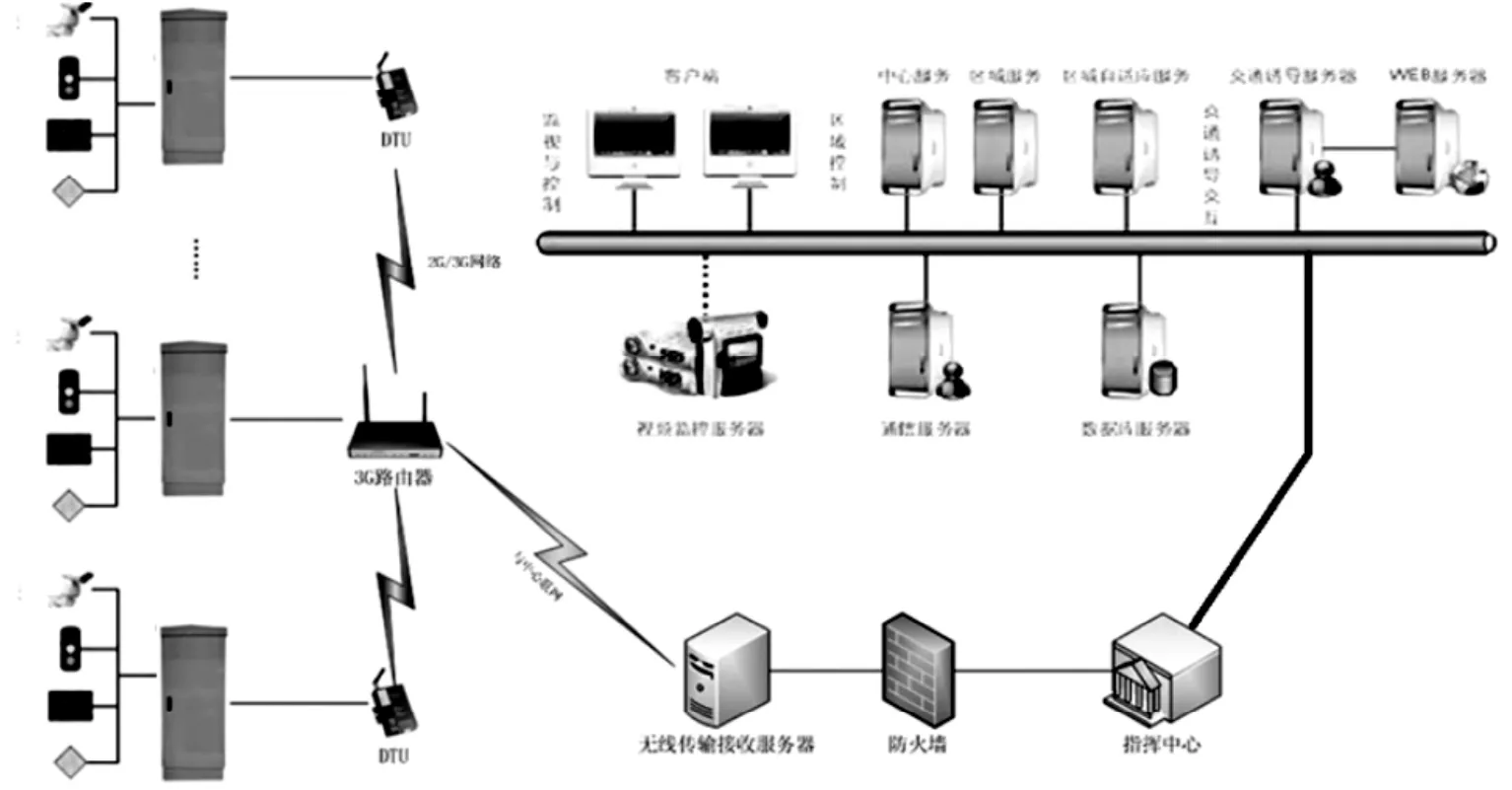
图3 系统架构图

1 优化模型的建立

交叉口间协调控制分为两种情况：单向协调和双向协调，单向协调即为双向协调仅考虑一个方向流量的特殊情况，比较简单，这里重点研究双向协调。

1.1 双向协调模型

在实际道路中，进入系统的车辆是不断增加的，对于系统内部而言，协调方向的车流也有支向车流的左转和右转汇入，所以在各个单独的交叉口，协调方向的车流到达是源源不断的，区别只是车

头时距的大小。因此，假设车流到达积累数和时间呈线性关系，流量的大小仅仅影响该线性关系的斜率。

车流以车队的形式经过各个交叉口，而车队车头在交叉口处受阻和车身在交叉口处受阻的情形是不同的，区别在于：车头受阻时，可能是头车前还有排队车辆，也可能是头车前无排队车辆，受阻等待的时间小于或等于一个红灯的时间；车身受阻时，前面没有排队长度，受阻等待时间为一个红灯时间，以下讨论两种情况下的协调模型。

1.1.1 下行车队在下一交叉口受阻

其车队头部受阻情况如图1所示。单相协调中交叉口设为i，下一交口为i+1，则交叉口i+1相对于i的相位差如公式(1)所示。

式中，1+→iiφ ——交叉口i+1相对于i的相位差(s)；1+→iil ——交叉口i到交叉口i+1的距离(m)；1+iS ——交叉口i+1处的由i向i+1流向的排队长度(m)；1+→iiv ——交叉口i到交叉口i+1间路段的平均速度(m/s)；1+iτ ——车队头部到达交叉口i+1处至开始消散的时间。

此时，车队头部受阻产生的延误如图2中阴影部分所示。

tr为整列车队到达交叉口后后续没有车辆跟来的时间，绿灯开启后，1+iτ 时间内累积的车辆全部疏散，t时间后进入交叉口的车辆不受阻的通过交叉口，因此有：

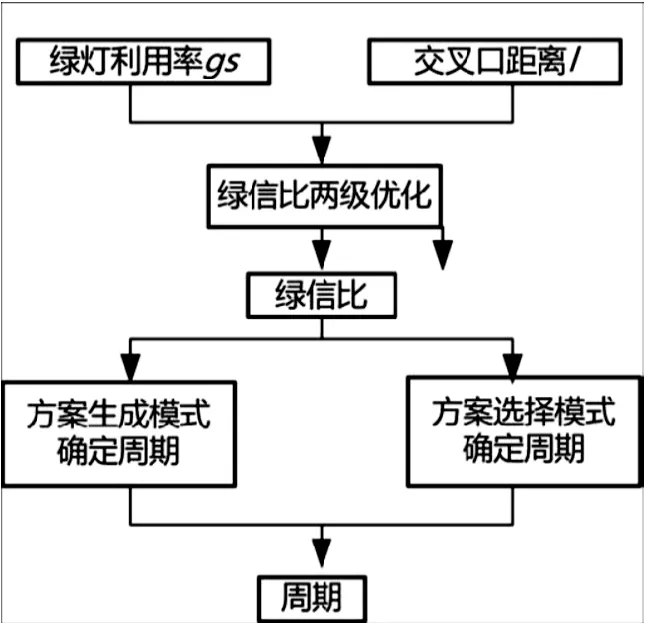
图4 算法结构流程图

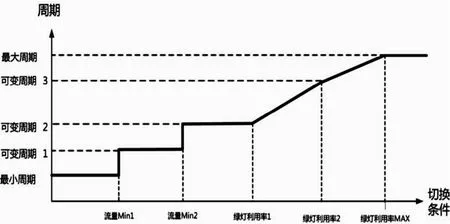
图5 周期的选择示意图

图6 绿信比的优化

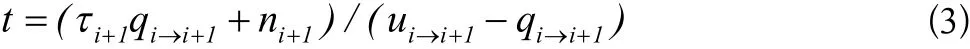
式中， qi→i+1——交叉口i+1到交叉口i+1的流量(pcu/s)；t——绿灯开启后排队长度消散时间(s)； ui→i+1——交叉口i到交叉口i+1的最大通行能力(pcu/s)； ni+1——排队车辆数。

可得到延误 di→i+1如公式(4)所示。

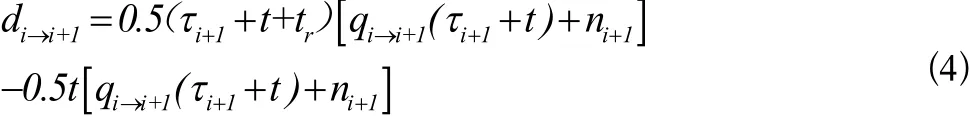
其中，tr在公式中是一个非负整数，并不影响最终结果，因此设tr为0。则 di→i+1的最终计算结果如公式(5)所示。

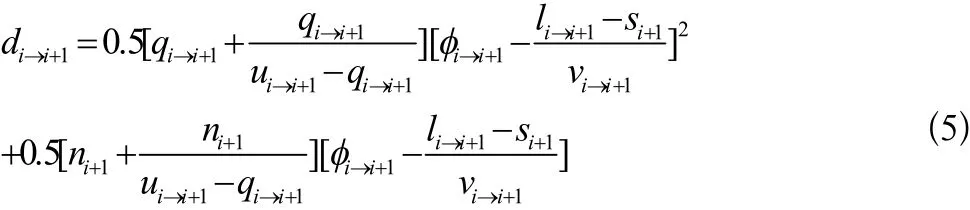
1.1.2 上行车队在下一交叉口受阻

双向协调的相位差在单向协调的基础上进行计算，首先按照下游车队延误的计算方法计算上游车队的延误。设上游相邻两个交叉口为i+1和i，显然，交叉口i对交叉口i+1来说相位差为：

式中，ii→+1φ ——交叉口i+1对交叉口i的相位差(s)；T——周期时长(s)。

与下行车队头部受阻的情形类似，计算得到上行车队的总延误如公式(7)所示。

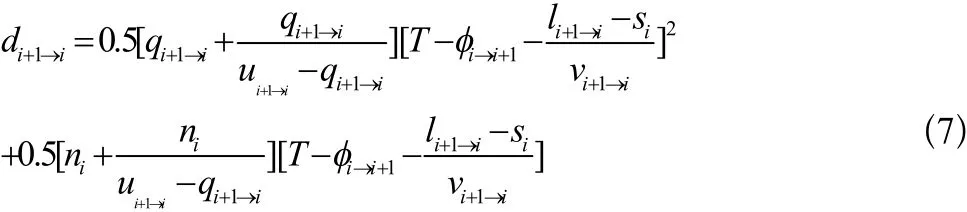
1.2 双向总延误

由公式(5)和(7)可得系统中双向的总延误如公式(8)所示。

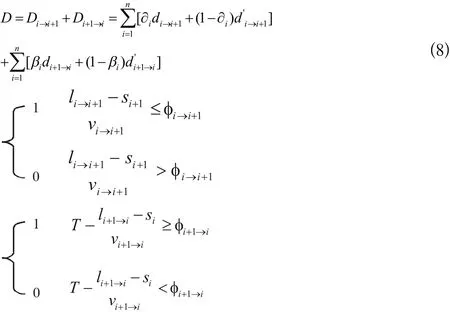
可见，双向协调问题最终归结为一个非线性规划求最优解问题，当总延误D最小时求出相位差的最优解。

1.3 约束条件

该模型的约束条件为路口实际流量小于道路最大流量，周期时间的长度大于设计相位差和路段计算相位差之和，即公式(9)所示。

2 参数选择

由上面介绍的双向协调相位差的计算模型，只需要得到路段流量，饱和流量，交叉口的排队长度，路段均速，相邻交叉口之间的距离，就能够通过模型得出相邻交叉口的双向相位差。

2.1 路段流量

路段流量由路口检测器获得，线圈检测到的流量为一周期统计一次，系统根据上三个周期的平均流量得出本周期预测流量。

2.2 路段均速

经过大量的数据分析，得出路段均速与流量之间的关系如下。(1)单车道情况：

(2)双车道情况：

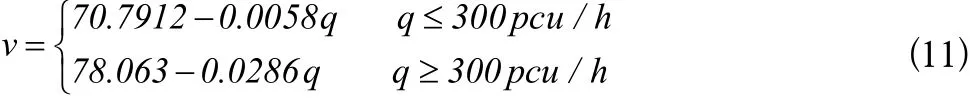
表1 子区划分表

表2 优化前喀什路-文光路当前配时表

表3 优化后喀什路-文光路当前配时表

表4 子区一相位差表

表5 各个路口优化前的停车次数及总延误时间

表6 各个路口优化后的停车次数及总延误时间

(3)三车道及三车道以上情况：

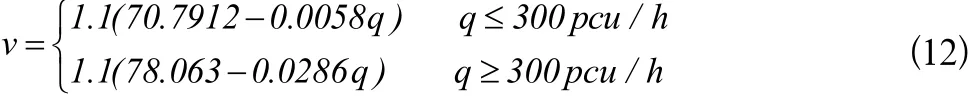
式中，q——停车线处线圈检测出的流量，本周期数据用于拟合下周期路段均速；v——路段均速。

各种情况系数可以累积，软件界面中增加车道数，有无分隔带的设置。

2.3 排队长度

(1)路段流量不饱和情况(绿灯利用率＜1)。

路口线圈能够检测到车辆的车头时距，当车头时距小于3s(此值可以手动设置)的时候，即认为此时统计到的车辆数是红灯相位排队的车辆，或是绿灯开启后汇入排队长度车辆的车辆数，该值为排队车辆数的最大值，用 N测表示。

排队车辆数计算公式如下：

式中，sN——排队车辆数；预测q ——停车线检测线圈三个周期的平均检测流量(pcu/s)。

排队长度根据交通工程饱和流量的定义，按照每辆车占地6米计算，即：

(2)路段流量过饱和情况(绿灯利用率≥1)。

此时中心软件应提出报警，排队车辆数选用 N测的数据。

3 信号控制系统

3.1 系统架构组成

系统采用三层分布式结构：中心层、通信层和路口层。信号机能够通过RS232/RJ45或者无线通讯实现与中心连接，本方案采用无线通讯形式组网。

针对乌鲁木齐市的实际情况和需求，设计系统架构如图3所示。其交通信号控制系统架构具体描述如下。

(1)信号控制中心。信号控制中心设备主要包括中心控制服务器、区域控制服务器、通信服务器、数据库服务器、客户端等，服务器安装在指挥中心，客户端既可以安装在指挥中心，主要用于监视和修改路口控制参数等。

(2)通信部分。通信部分主要包括无线通讯模块(DTU)和通信网络，本方案中采用无线通讯模块(DTU)通过GPRS/3G无线网络与中心设备相连。

(3)外场部分。外场部分设备主要包括信号机、检测器等，信号机根据车辆检测器检测的交通信息(包括车流量等)实时调整路口控制方案(信号周期和绿信比)，实现路口的有序控制。

3.2 原理分析

信号控制原理是通过两级优化体系实现区域协调自适应控制。

一级优化是中心完成周期、绿信比、相位差等参数的计算或选择，直接下发给信号机执行；二级优化是信号机根据具体的车辆个体到达需求和相位差限制，对绿灯长度作微调。

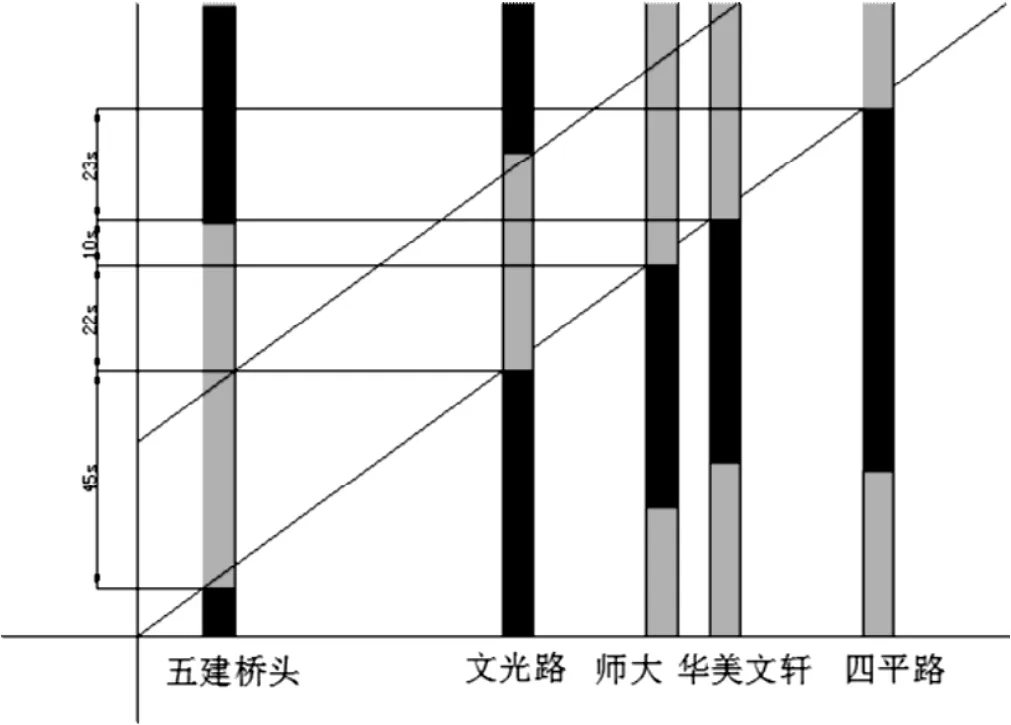
图7 喀什路子区一晚高峰时距图

优化的目标是绿灯利用率达到最高，子系统交叉口延误达到最小。周期长、绿信比、相位差选择与计算的主要依据是“绿灯利用率”。其算法结构流程图如图4所示。

3.2.1 周期选择模型

周期长方案优选包括5套方案：最小周期、可变周期1、可变周期2、可变周期3、最大周期，其选择示意图如图5所示。

3.2.2 绿信比计算模型

协调控制下，计算绿信比时，关键交叉口绿信比的计算方法与单点优化绿信比的计算方法相同，要根据关键交叉口进行调整，两者所应用的流量都为预测流量，非实测流量。

首先，确定相位的最小绿灯时间：各交叉口协调相位所必须保持的最小绿灯时间就是关键交叉口协调相位的绿灯显示时间，ming为取整后所得：

式中，ming ——关键交叉口协调相位的有效绿灯时间；L——交叉口进口道处路宽，包括非机动车道宽度，无调查值情况下，双向四车道取16m，双向六车道取25m；行人v ——行人过街速度，该值应由老年人的平均行走速度决定，取0．9m/s。

最小绿灯时间计算得出以后，可以得出在周期中每个相位的绿信比。系统根据检测到的绿灯利用率对绿信比进行小步距优化，进行绿信比一级优化。然后按照图6完成绿信比二级优化。

4 实际路况分析

所建立的优化模型和优化算法采用对实际路况的分析进行验证。以喀什路沿线从喀什路五建桥头到喀什路天津路的各个路口为实验对象，共有10个路口，将其划分为两个区域，如表1所示。

4.1 喀什路沿线路况分析

运用本文设计的交通配时优化模型，即公式(8)，将各个子区调查的交通参数代入，经过计算机迭代计算，进行优化。

以喀什路-文光路这个路口为例，其距离上一个路口为300mm，其优化前当前配时表如表2所示。

优化依据：延长协调相位的绿灯时间，同时增加东进口左转时间，由之前的15s增加到25s，第二个单口放行相位保持不变，增加部分南北进口的放行时间，得到优化后的配时表如表3所示。

依次计算得到喀什路子区一晚高峰时距图，如图7所示。

根据时距图可以清晰看出车流由东向西行进时各个路口的相位差，如表4所示。

4.2 优化前后效果的对比

在没有利用本文介绍的交通模型优化前，各个路口的延误以及停车次数如表5所示，优化以后，经过实际的交通调查，得出表6的结果。

可见，经过本文设计的模型优化以后，总延误以及停车次数都得到了降低，因此，该交通模型是适用于乌鲁木齐城市道路的。

5 结语

本文根据目前乌市道路平面交叉口与信号配时的特点，对城市道路交叉口的基础理论进行了研究，研究了影响信号控制交叉口的因素和参数；建立了流量大小、排队和绿信比信号优化模型；通过对喀什路上两个交通子区进行模型的实际验证，结果表明通行效果良好，验证了模型和算法的有效性。

[1]陈小红,钱大琳.基于互补问题的混合交通信号配时优化模型[J].系统工程理论与实践,2010,30(1):184-191.

[2]张存保,冉斌.车路协同下道路交叉口信号控制优化方法[J].交通运输系统工程与信息,2013,13(03):40-45.

[3]陈传明,张铃.智能交通信号灯配时及优化设计 微机发展 2005 15(03):4-6.

[4]柴琳果.基于车路协同系统的交通仿真方法研究[D].北京交通大学,2012.

[5]贺明.城域交通冲突点控制策略研究[D].浙江大学,2008.

At present, urban traffic congestion problem seriously affected the living quality of urban residents in China, and restricted urban economic development. This raised higher requirements for signal timing at urban road intersections. Combined with current condition of traffic congestion in Urumchi, according to its characters of plane intersection signal timing, this paper presented a cooperative control optimization problem with three indexes: delay time, queue length, and traffic capacity. Then the signal optimal model is constructed. Finally, the presented plane intersection signal timing optimization model is verified by experimental analysis of real plane road intersection traffic conditions.

Complex Traffic Network;Cooperative Control;Signal Optimization Model

何玮(1979—),女,新疆乌鲁木齐人,回族,2008级工程硕士,研究方向:智能交通。

梁坤。