基于遗传过程神经网络算法的航空发动机健康状态图谱化预测方法

杜党党，贾晓亮，郝超博

（1.西北工业大学 机电学院，陕西 西安 710072；2.解放军95631部队，四川 泸州 646001）

0 引言

通过有效预测和分析航空发动机的性能参数，可以估计发动机未来一段时期的健康状态，对预防和排除发动机的故障及安全隐患、统筹规划发动机执行任务的梯次、合理配置各类保障资源、优化维修策略、更好地推行视情维修的理念，具有非常重要的意义。

状态监测数据是航空发动机内在状态的外在表现，预示着其未来健康状态的发展趋势。然而，由于发动机性能参数具有非线性、非平稳性、高维性、不确定性、混沌性和时变性等特征，使用传统的线性时间序列预测模型会带来较大的误差［1-2］。过程神经网络（Process Neural Network，PNN）可以在任意误差精度内逼近任意连续函数，具有强大的非线性映射能力，特别是它考虑了参数在时间维度上的累积效应，放宽了神经元对输入变量的同步瞬时限制，因此用于非线性时间序列预测具有明显的优势［3-6］。然而，PNN 存在网络结构特别是隐层节点数难以确定、训练过程易陷入局部极小等问题，影响了其实际应用效果。

航空发动机是一个复杂系统，不同的性能参数分别从不同的层面和角度动态地反映着发动机的健康状态。由于在工程中简单易行，大多数性能预测主要针对单一参数进行［6-7］，但是忽略了其他参数中包含的有用信息，预测单一参数可能导致分析结论出现较大偏差［8］。多参数预测客观反映了发动机由多个系统组成、多个功能模块协调工作的复杂机理，正成为发动机健康状态预测研究的热点［8-10］。预测结果具有耦合性、高维性和非线性等特性，对进一步系统有效地分析其中包含的有用信息、合理可靠地得出预测结论至关重要，目前多参数预测主要采用信息融合方式。文献［8］采用传感器数据级融合方法构建综合健康指数，用于系统性能衰退评估和剩余寿命预测；文献［9］利用贝叶斯线性模型融合多源信息，进而预测发动机性能衰退的趋势；文献［10］利用状态监测信息和智能预测方法实时评估和预测设备的失效概率。尽管融合分析的最终结果所含的信息量比任何单一参数的信息量都大，但因其有效性受制于所提取特征信息的准确性，无法避免融合过程中细节信息的缺损，以及多个信息源的引入可能导致预测精度下降，给得出预测结论带来了新的不确定性。此外，该方法还存在过程复杂繁琐、计算开销大、预测结果难以解释等问题。

基于此，本文采用相空间重构理论构造训练样本集，并结合遗传算法优化设计PNN 及其初始权值和阈值，通过优化后的遗传过程神经网络（Genetic Algorithm-Process Neural Network，GA-PNN）模型输出发动机的预测性能矩阵；对矩阵中的元素加以着色，构造代表发动机性能的预测图谱，借助图谱反映信息直观清晰、整合力强的优势，从系统层面快速预测发动机的健康状态。

1 面向航空发动机健康状态图谱化预测的知识准备

1.1 发动机健康状态的矩阵描述

定义1 样本性能矩阵。设反映发动机健康状态的性能参数有n个，按照周期τ采样，经过l个采样周期，共收集l×n个数据，可以构造一个l×n维的矩阵X，称为样本性能矩阵。样本性能矩阵系统地反映了发动机某段时期健康状态的时空分布规律，记为

式中xij表示参数j在第i时刻的值。显然，矩阵X的行值代表时刻i所有参数基于空间序列的分布，列值代表参数j基于时间序列的分布。

定义2 预测性能矩阵。对样本性能矩阵中的每一个参数分别进行预测，将预测得到的每个参数按照时序重新组合，构成新矩阵Pl′×n，称为预测性能矩阵。预测性能矩阵代表发动机未来一个时期的健康状态。

1.2 发动机时间序列样本的相空间重构

为克服发动机非线性混沌时间序列样本中不确定性因素的影响，引入相空间重构理论，以最大限度地挖掘输入输出之间的对应关系。相空间重构理论将时间序列中的点序列按照嵌入维数映射到相空间中对应的点，这些点组成的轨迹能够再现或继承原始系统变量间的运行规律及其运行状态特性，提高非线性时间序列模型的泛化能力［11］。

根据嵌入定理，对于时间序列｛xi｝ni=1，当前状态的信息可以表示成m维矢量

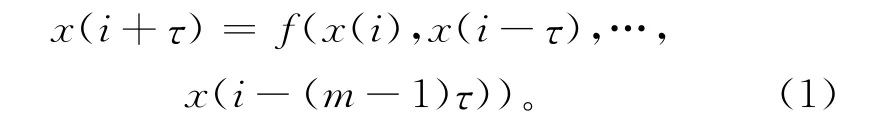
式中：m为嵌入维数；τ为延迟时间，常取采样周期间隔。式（1）构造了输入与输出之间的映射关系f：Rm→R，即只要知道特定的m个x（i），x（i-τ），…，x（i-（m-1）τ），就可以确定x（i+τ），从而为训练样本集的构建和网络结构设计提供依据。由于映射函数f难以获得精确的数学解析形式，下面将选择PNN 逼近f。

1.3 过程神经网络模型

对于一个典型的m-q-1三层前向PNN，其模型如图1所示。

网络的输入与输出关系可表示为

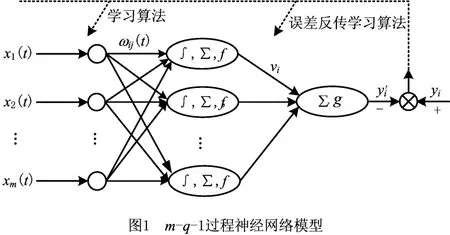
式中：ωij（t）为隐层第i个过程神经元和输入层第j个神经元之间的权函数；θi为隐层第i个神经元的阈值；vi为隐层第i个过程神经元和输出层神经元之间的权值；［0，T］为输入过程区间；u和g分别为隐层过程神经元和输出层神经元的激励函数。本文取u为Sigmoid函数，g为线性函数。

采用C［0，T］空间上的正交基函数将输入函数和权函数展开，则式（2）可以简化为

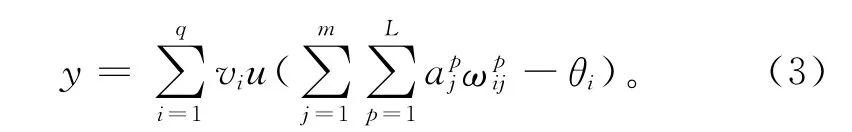
给定k组学习实例，其中网络第i次的输入Xi=［xi-1（t），…，xi-m（t）］，用yi和y′i分别表示网络第i次的实际输出和期望输出，则网络的误差函数可以表示为

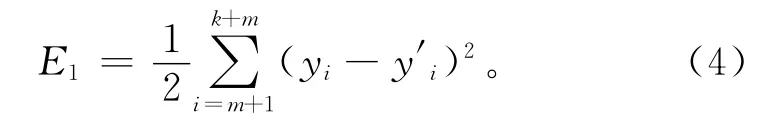
1.4 预测图谱

针对预测性能矩阵Pl′×n中隐含的有用信息难以直观、快速、系统的挖掘问题，受文献［12］启发，对P中的元素逐列执行标准化，按照设定的编码规则加以着色，依时序画出由l′个彩色单元连接而成的n条图谱色带，进而通过组合色带构造出预测图谱。预测图谱的时间维表征各个参数基于时间分布的变化趋势，空间维表征不同参数基于空间分布的耦合关系，反映了系统信息流的时空演变趋势，表达了其内部工作机制的有序性、稳定性和平衡性。如果将样本性能矩阵和预测性能矩阵合并转化为图谱，则可以从更大的时空范围审视系统的健康状态。

当系统处于衰退的正常水平时，即使其状态数据在一定范围内波动，其内部各个要素之间依然会保持一种相对的动态平衡。表现在图谱上，色差过渡相对自然柔和，色带颜色变化呈现随机的小幅波动和可以容许的紊乱，纹理基本协调，整体上具有平稳与和谐之美。值得警惕的是，一旦系统多个数据几乎同时发生突变或某一参数多次出现突变，图谱对应的区域色彩必然出现明显的跳变和波动，此时色差过渡突然，整体协调性变差，预示着系统的健康状态很可能出现异常或恶化。

如果预测图谱与实际图谱对应区域的颜色完全一致，则认为该区域二者对应的数值相同。如果对应区域的颜色在色谱刻度尺上距离较近，则表明二者对应的数值比较接近，否则意味着预测值与实际值之间有较大的差别。通过式（5）［13］计算预测图谱与实际图谱中对应区域的相似度，评价预测图谱的预报能力。R越大，说明二者拟合程度越高，预测图谱的整体预报能力越强。

2 面向航空发动机性能预测的GA-PNN算法

2.1 基于GA 的PNN 结构优化设计

PNN 结构参数如输入层、隐层以及输出层的节点数等因素，在一定程度上影响网络的泛化能力和预测精度。由于网络的结构参数没有统一的设计规则，通常采用试错法进行参数选择，这对于多参数预测的情形是难以接受的，尤其试错选择的结果未必最佳。因此，有必要对网络结构进行合理设计。

对于待预测的参数，可将其连续m个数据拟合成一个时变函数作为PNN 的输入，参数本身是预测的输出目标，故设置输入和输出层的节点数均为1。运用经验公式限定隐层节点数的范围（m和n分别为嵌入维数、输出层节点数，a为1～10之间的整数［14］）。

由于GA 具有强大的全局搜索和并行处理能力，能够快速搜索到全局最优点，不易落入局部最小点，可以用来优化PNN 的隐层节点数q。在综合收敛精度和收敛速度两个指标的基础上，使用精敛比作为个体适应度函数。

式中：E0和E1分别为设定的收敛精度和实际收敛精度，t为网络训练时间。

具体做法如下：将q的初始值进行二进制编码，采用精敛比表示个体的适应度函数；设置种群数、进化代数、交叉率和变异率，使用一部分样本训练网络，用其余的样本测试，计算所有个体的平均适应度值；对种群中的个体进行选择、交叉和变异等操作，得到优化后的适应度值；当所有个体平均适应度值达到要求或达到最大的进化代数时结束迭代，否则继续进行选择、交叉和变异等操作。q值一旦确定，就完成了PNN 的拓扑结构优化设计。

2.2 基于GA 的PNN 初始权值和阈值的优化设计

测试发现，对于相同的训练样本集和同一初始训练速度，用测试样本对训练好的网络进行测试，结果并没有达到预期精度，说明网络训练时陷入了局部极小值。为了消除训练时的初始权值和阈值对PNN 收敛精度的影响，再次引入GA 优化网络的初始权值和阈值。

优化过程与隐层节点数的优化过程类似，这里不再赘述。需要说明的是，本文的个体适应度函数采用误差函数E1。

2.3 基于GA-PNN算法的发动机预测性能矩阵的输出步骤及流程

2.3.1 基于GA 优化PNN 隐层节点数和初始权值阈值的主要步骤

前面的分析表明，隐层节点数及训练时的初始权值阈值对PNN 模型的预测效果影响较大。因此，本文选用GA 分别优化PNN 隐层节点数和初始权值阈值，优化的主要步骤如下：

步骤1 构造参数j的训练样本集，设定种群数、进化代数、交叉概率、变异概率等参数，初始化隐层节点数q的种群并进行编码。

步骤2 使用个体对q赋值，通过训练，根据式（6）计算每个个体的适应度。按照轮盘赌法选择个体，实施单点交叉、变异等操作，得到优化后的适应度值。

步骤3 若达到设定的迭代次数或者适应度值满足要求，则输出优化的隐层节点数；否则转步骤2，继续进行迭代。

步骤4 确立PNN 最优的结构后，设置GA 参数，对网络初始权值和阈值进行初始化并编码。

步骤5 使用个体对权值和阈值进行赋值，根据式（4）计算训练后每个个体的适应度。实施选择、交叉、变异等操作，得到优化后的适应度值。

步骤6 若达到设定的停止训练条件，则输出优化的初始权值阈值，退出优化程序；否则转步骤5，继续进行迭代。

2.3.2 GA-PNN 算法的主要步骤及预测性能矩阵的输出流程

算法的主要步骤如下：

步骤1 使用参数j优化的PNN 结构以及初始权值和阈值。设定网络的训练收敛精度ε、最大迭代次数M、累积学习迭代次数s等参数。

步骤2 选取合适的正交基函数，将输入函数和权函数分别展开。

步骤3 将全部训练样本输入网络，使用式（3）计算网络的输出yi。

步骤4 使用式（4）计算网络的误差函数E1。若E1＜ε，或者s＞M，则转步骤6。

步骤5 按照LM（Levenberg-Marquardt）方法［5］更新网络权值和阈值，令s+1→s，转步骤4。

步骤6 保存当次网络学习结果，并利用训练好的网络计算参数j的预测值。

待所有参数预测完毕，合并预测结果并输出预测性能矩阵，退出程序。

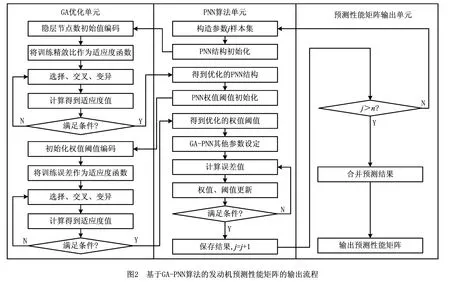
图2所示为基于GA-PNN 算法的发动机预测性能矩阵的输出流程图。

3 基于GA-PNN算法的发动机健康状态图谱化预测方法的应用研究

综合考虑某型航空发动机使用的讲义、维修大纲以及工程师的经验等，选取排气温度EGT、高压转子转速N2、低压转子转速N1、燃油流量FF、高压压气机出口压力PB、低压压气机出口压力P2.5、低压涡轮出口压力P4.95、高压压气机出口温度T3、低压压气机出口温度T2.5、振动值VD、扭力值TO 11个参数表征该型发动机的性能。

3.1 基于GA-PNN 算法的发动机预测性能矩阵的输出

采用该型112号（假定）发动机的两次较大维修间隔期间，对巡航状态下的数据进行预测。抽样间隔为10个飞行架次，数据总数为163×11，即包含上述11个参数同期的各自163个数据。对于任一参数j（j=1，2，…，11），将其连续mj个数据拟合成一个时变函数作为预测模型的输入（mj表示参数j的嵌入维数），以第mj+1 个数据作为预测模型的相应期望输出，构建163-mj组样本。用前153-mj组样本对模型进行训练，用后10组样本进行预测验证（为了保证最终能够生成一个预测性能矩阵，算法要求每个参数用来预测验证的样本组数均相同）。具体做法如下：设GA 的种群数为30，进化迭代次数为30，交叉概率为0.5，变异概率为0.05，编码长度为5位。按照2.3.1节的步骤优化该参数对应的GA-PNN 的隐层节点数和初始权值、阈值，然后按照2.3.2节的算法利用该参数的训练样本对优化的GA-PNN 模型进行训练（使用6个勒让德正交基函数展开网络的输入函数及权函数），最后将测试数据代入训练合格的网络，对该参数后10个预测值进行预测。待所有参数预测完毕时合并预测结果，输出大小为10×11的发动机预测性能矩阵。表1所示为各参数对应的GA-PNN 模型的嵌入维数和最优拓扑结构。

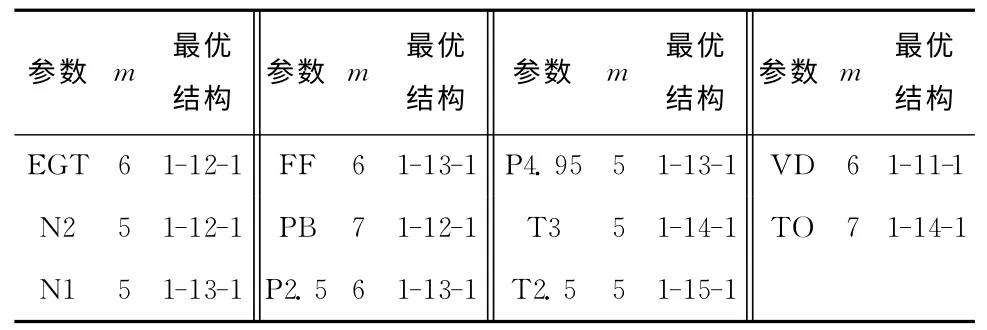
表1 GA-PNN模型嵌入维数及最优拓扑结构

为进行对比，使用单纯的PNN模型、基于GA 仅优化结构的PNN模型（记为GAL-PNN）、基于GA 既优化结构又优化网络初始权值和阈值的PNN 模型（记为GA-PNN），对上述参数分别进行4轮预测。所有模型的输入输出层节点数均为1。对于同一预测参数，PNN隐层节点数由经验公式确定（不同轮次测试中，允许2.1节中的经验公式包含的变量a适当地改变），后两种网络采用表1中的最优结构。前两种网络训练时每轮使用相同的初始权值和阈值，但不同轮次的初始权值和阈值并不同，GA-PNN使用优化的初始权值和阈值。主要测试各模型预测的平均相对误差AE、最大相对误差AEmax、相似度R和单轮累计耗时T等指标，结果如表2所示，表中。

表2 模型预测结果对比分析

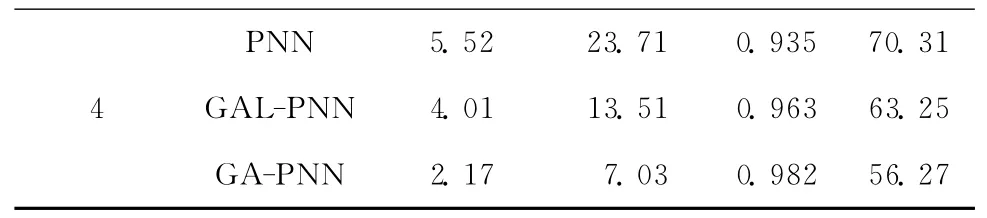
续表2

由表2可知，在4 轮测试中，GA-PNN 模型的平均误差最高为2.34%，最低为1.46%，优于平均误差最高为4.55%、最低为3.35%的GALPNN 模型，而PNN 模型平均误差最高为6.25%，最低为4.17%，在三者之中居于末位。就最大相对误差而言，GA-PNN 模型最高为9.12%，分别低于GAL-PNN 模型的12.63% 和PNN 模型的27.07%，反映了GA-PNN 模型的稳定性良好。特别是GA-PNN 的最低相似度为0.978，分别高于GAL-PNN 模型的最高相似度1.45%和PNN 模型的最高相似度4.6%，表明GA-PNN 的预测值与真实值在整体上非常接近。此外，GA-PNN 的耗时在三者中也具有一定优势。可见，尽管训练的初始条件有变化，但完成两次优化的GA-PNN模型的预测效果好于单次优化的GAL-PNN 模型和单纯的PNN 模型。之所以GA-PNN 模型的精确性、泛化性和稳定性最理想，主要得益于利用GA 在大范围内并行搜索得到了网络的最佳结构，提升了网络的泛化能力，而初始权值和阈值的优化则进一步修正了网络收敛方向，消除了陷入极小值的缺陷。因为GAL-PNN 模型采用优化的网络结构，所以效果相对好于PNN 模型。需要说明的是，尽管后两种模型存在一些不足，但就上述指标总体考量，并非意味着它们不能用于发动机性能参数的预测。

为了进一步检验GA-PNN 模型的泛化性和可靠性，使用该模型对机队中的另一台011号（假定）发动机的一组巡航阶段运行数据进行同步预测。数据总数为248×11，即11个参数同期各记录248个数据，采样间隔为10个飞行循环。将任一参数的连续m个数据拟合成一个时变函数作为预测模型的输入（m表示该参数的嵌入维数），以第m+1个数据作为预测模型的相应期望输出，构建248-m组样本。使用前230-m组样本进行GA-PNN 建模，用后18组样本进行预测验证，GA 参数的设置和基函数选取与上例相同。所有参数预测完毕后，将11个参数的预测结果进行合并，输出18×11的预测性能矩阵。预测结果同样表明，GA-PNN 模型能够满足工程中发动机性能监控的需要。表3和表4所示分别为011号发动机各参数GA-PNN 模型的嵌入维数、最优拓扑结构和预测结果分析。

表3 GA-PNN模型最优拓扑结构

表4 基于GA-PNN模型预测结果分析

3.2 发动机健康状态的图谱化预测

将训练数据和预测数据合并转化为图谱，可以从更大的时空范围系统地审视发动机的健康状态变化趋势。图3～图4中，上部为实际样本性能矩阵生成的图谱（实际图谱），中部为训练数据和预测数据合并后生成的图谱（预测图谱），下部为图例尺，图例尺的刻度0%～100%表示对应参数的标准值由最小到最大依次改变。图谱中横轴表示数据编号，纵轴表示参与预测的参数编号。表5所示为各参数与色带编号之间的对应关系。

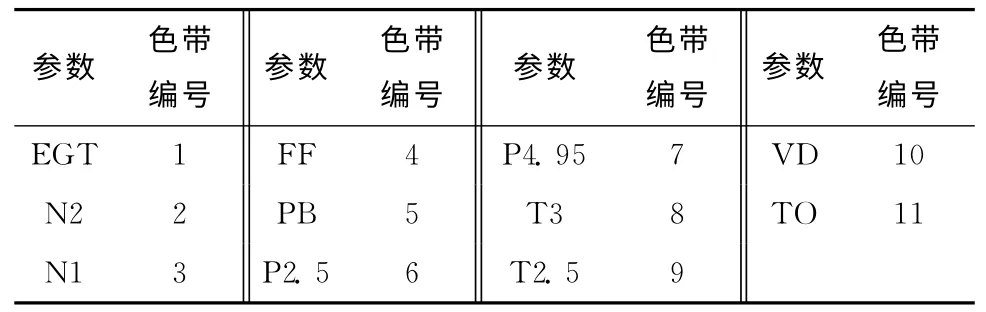
表5 参数与色带编号之间的对应关系

3.2.1 实例1

图3为112号发动机第3轮测试时，GA-PNN算法输出的预测性能矩阵生成的图谱。

图3中A 段图谱波动较小，色彩变化相对流畅，系统此阶段处于健康状态；B段图谱呈现较大波动，色彩突变明显，系统此阶段处于快速衰退状态。

从图3的验证区可以看出，预测图谱与实际图谱对应的部位在时空分布上非常相似：色带颜色变化、纹理结构走向大致趋同，色彩波动相对一致，表明预测数据与实际数据总体上比较吻合。根据式（5）计算预测图谱与实际图谱之间的相似度为0.983，说明预测图谱具有较强的预报能力。

在A 段图谱中，该发排气温度、燃油流量、高低压转子转速等参数对应的图谱色带波动趋势在时间维度上总体保持一致，表明其变化均能反映发动机的性能衰退水平。然而，不同色带的波动幅度在空间维度上并不完全同步，说明各个参数表征性能衰退趋势的权重和灵敏度不尽相同，系统个别单元之间的协调性不够理想。上述现象可能与该发燃油调节系统的延迟性、参数测量误差、环境变量的影响以及某一参数对其他参数波动过程中的补偿作用等因素有关。但就总体而言，图谱色差过渡相对自然柔和，波动幅度处于可以容许的范围，表明该时期发动机的健康状态基本正常。

而在B 段图谱中，图谱多条色带条纹开始紊乱，色差过渡突然，特别是纵向之间出现较大幅度的波动，且扭力对应的色带11一直偏小，说明该发整体平衡关系受到破坏，其内在的秩序性、稳定性变差，衰退趋势加速，需要加强健康监控，防止出现异常。期间，工程维修部门采取了一些防范该发动机性能继续恶化的措施，但效果并不理想。在完成第163个飞行周期后，经维修基地评估，对该发动机做出提前返厂的建议。需要指出的是，仅从色带1来看，排气温度值并未出现较大幅度的波动和增加，说明如果完全依赖单一参数，则有可能会得出不可靠的预测结论。

3.2.2 实例2

以图4所示的011发动机的预测性能矩阵对应的图谱为例。图中图谱色带横向过渡自然柔和，纵向之间协调性好，色彩变化整体比较平稳，表明系统处于健康状态

分析图4可知，验证区域除了个别数据点的颜色有小幅差别外，其余大部分对应的区域均保持一致，计算预测图谱与实际图谱之间的相似度为0.978，表明预测值与实际值的偏离度较小，预测图谱能够预报发动机的健康状态。

在时间分布上，除局部短暂的突变区域外，图谱色带的走向相对柔和平缓，反映了随着时间的变化，相应的子系统性能变化温和可控，尤其是色带11的波动非常小，说明发动机的输出扭力稳定可靠，几乎不受其他参数改变的影响；在空间分布上，部分色带之间存在清晰的相关性（如第1、2条），说明这些参数之间本身具有同样的相关性，也表明系统的各子单元之间协调性较好。图谱整体波动性小，平稳协调，预示着该发动机未来一个时期依然呈现正常且缓慢衰退的趋势，总体健康状态良好。

可见，预测图谱能够客观、清晰、系统、并行地表达发动机健康状态的演变趋势及规律。当然，工程师可以根据实际分析的需要，灵活选取预测参数，进而通过动态地调整预测图谱中的色带来改善图谱预测的效果。

4 结束语

本文针对PNN用于航空发动机性能参数预测时结构难以设计、训练易陷入极小值的缺陷，以及预测结果中隐含的健康信息难以清晰、快速识别的问题，提出一种基于GA-PNN算法的发动机健康状态图谱化预测方法。首先，采用相空间重构理论构造训练样本集并结合遗传算法，优化设计PNN 结构及初始权值和阈值，进而生成预测性能矩阵；其次，对预测性能矩阵中的元素加以着色处理，构造代表发动机健康状态的预测图谱。验证结果表明：GA-PNN模型网络结构合理可靠，有效地消除了网络训练中易陷入极小值的缺陷，模型的精确性、稳定性和泛化性得到了明显的提升；借助于预测图谱，可以清晰、直观、系统地展示发动机多个预测参数之间的非线性、耦合性关系及其时空分布全貌，快速挖掘预测性能矩阵中隐含的健康信息，提高了异常成分和模式的识别效率。该预测方法实现了从系统层面精准、高效、直观地预测发动机健康状态的目的，为发动机等复杂系统健康状态的预测、监控及决策提供了新的思路和手段。

下一阶段，将在完善发动机故障图谱库的基础上，应用数字图像匹配算法，深入研究基于图谱的航空发动机典型故障模式预测方法。

［1］LIN Jiewei，ZHANG Junhong，ZHANG Guichang，et al.Aero-engine blade fatigue analysis based on nonlinear continuum damage model using neural networks［J］.Chinese Journal of Mechanical Engineering，2012，25（2）：338-345.

［2］TOBON-MEJIA D A，MEDJAHER K，ZERHOUNI N，et al.A data-driven failure prognostics method based on mixture of gaussians hidden markov models［J］.IEEE Transactions of Reliability，2012，61（2）：491-503.

［3］ZHONG Shisheng，CUI Zhiquan，WANG Tichun.Prediction of engine gas path parameter deviation based on fractional aggregation process neural network［J］.Computer Integrated Manufacturing Systems，2013，19（5）：1071-1077（in Chinese）.［钟诗胜，崔智全，王体春.基于分式聚合过程神经网络的发动机气路参数偏差值预测［J］.计算机集成制造系统，2013，19（5）：1071-1077.］

［4］GE Li，YIN Guisheng.Application of process neural network on consumer price index prediction［C］／／Proceedings of International Conference on Affective Computing and Intelligent Interaction.Berlin，Germany：Springer-Verlag，2012：427-432.

［5］DING Gang，FU Xuyun，ZHONG Shisheng.Aeroengine performance parameters prediction based on process neural network［J］.Computer Integrated Manufacturing Systems，2011，17（1）：198-207（in Chinese）.［丁 刚，付旭云，钟诗胜.基于过程神经网络的航空发动机性能参数预测［J］.计算机集成制造系统，2011，17（1）：198-207.］

［6］DING Gang，WANG Xiongwei，LEI Da.Aeroengine exhaust gas temperature prediction using process neural network with time-varying threshold functions［J］.Applied Mechanics and Materials，2013，423-426：2341-2346.

［7］LIU Zhiguo，CAI Zengjie，TAN Xiaoming.Forecasting research of aero-engine rotate speed signal based on ARMA model［J］.Procedia Engineering，2011，15：115-121.

［8］LIU Kaibo，GEBRAEEL N Z，SHI Jianjun.A data-level fusion model for developing composite health indices for degradation modeling and prognostic analysis［J］.IEEE Transactions on Automation Science and Engineering，2013，10（3）：652-664.

［9］WANG Huawei，WU Haiqiao.Residual useful life prediction for aircraft engine based on information fusion［J］.Journal of Aerospace Power，2012，27（12）：2749-2755（in Chinese）.［王华伟，吴海桥.基于信息融合的航空发动机剩余寿命预测［J］.航空动力学报，2012，27（12）：2749-2755.］

［10］CAESARENDRA W，WIDODO A，THOM P H，et al.Combined probability approach and indirect data-driven method for bearing degradation prognostics［J］.IEEE Transactions on Reliability，2011，60（1）：14-20.

［11］CHEN Diyi，DING Cong，MA Xiaoyi.Nonlinear dynamical analysis of hydro-turbine governing system with a surge tank［J］.Applied Mathematical Modeling，2013，37（14／15）：7611-7623.

［12］DU Dangdang，JIA Xiaoliang.Health state monitoring for aero-engine based on dynamic standard color-picture［J］.Computer Integrated Manufacturing Systems，2013，19（12）：3068-3074（in Chinese）.［杜党党，贾晓亮.基于动态标准彩色图谱的航空发动机健康状态监控［J］.计算机集成制造系统，2013，19（12）：3068-3074.］

［13］LI Jiaqing，CHEN Jin，SHI Chongjiu.Fault diagnosis method based on acoustic holography［J］.Journal of Mechanical Engineering，2009，45（5）：34-38（in Chinese）.［李加庆，陈进，史重九.基于声全息的故障诊断方法［J］.机械工程学报，2009，45（5）：34-38.］

［14］HAN Liqun.Artificial neural network theory，design and application［M］.Beijing：Chemical Industry Press，2007（in Chinese）.［韩力群.人工神经网络理论、设计及应用［M］.北京：化学工业出版社，2007.］