变采样间隔自适应EWMAt控制图统计设计

常志远，孙金生

（南京理工大学 自动化学院，江苏 南京 210094）

0 引言

1924年，Shewhart博士设计了均值控制图，作为一种有效的统计质量控制方法，控制图在科学研究与工业生产中得到了广泛的应用。随着科技的发展，生产过程越来越复杂，早期的控制图渐渐不能满足对生产过程监控的需求。因此，学者们也在不断地改进控制图的设计方法。

针对Shewhart控制图对小偏移不敏感的问题，1959年Roberts［1］提出指数加权移动平均（Exponentially Weighted Moving Average，EWMA）控制图，这种控制图具有设计简单、对小偏移敏感的特性。EWMA 控制图提出后受到了广泛的关注，学者们对此进行了深入研究。例如：Lucas等［2］深入研究了EWMA 控制图的特性，给出了计算EWMA控制图平均链长ARL的Markov 链方法；Capizzi等［3］将自适应EWMA 滤波方法应用于EWMA 控制图，提出自适应EWMA（Adaptive EWMA，AEW-MA）控制图，该控制图方法可以克服常规EWMA控制图只对固定偏移敏感的问题；Woodall等［4］给出了表征控制图“惯性（inertia）”的量化指标，并且指出AEWMA 控制图要优于常规EWMA 控制图；Saccucci等［5］提出变采样间隔EWMA（Variable Sampling Intervals EWMA，VSI-EWMA）控制图，将变采样间隔技术引入EWMA 控制图，提高了EWMA 控制图的检测速度；Lee等［6］深入研究了多变量VSI-EWMA 控制图，并给出了控制图最优设计算法；薛丽［7］给出了同时检测均值和标准差的EWMA 控制图的经济设计模型，并优化了控制图参数。此外，胡雪龙等［8］考虑带有辅助样本的X（Supplematary Sample X，SSX）控制图的经济设计，通过模式搜索算法对费用函数进行优化，得到了SSX 控制图的最优决策变量。

以上控制图设计方法均需假设第一阶段的参数估计是准确的，但是这种假设在实际中很难做到，当方差估计不准确时，会造成控制图的误报漏报率大大增加。针对该问题，Zhang等［9］提出t控制图，证明当服从标准正态分布的检测变量出现均值漂移时，均值与标准差的比值服从非中心t分布，并指出t控制图的优势在于控制限与方差没有直接关系，而是样本大小的函数；Caleno 等给出了短周期下Shewhartt控制图的经济设计模型［10］；Castagliola等给出了短周期下变样本大小的t控制图的设计方法以及性能分析［11］；Kazemzadeh 等研究 了VSIEWMAt控制图的特性，并给出了VSI-EWMAt控制图的优化设计方法［12］。VSI-EWMAt控制图的缺点在于固定的参数只对固定的偏移敏感，小的平滑系数会导致控制图对大偏移检测的严重滞后。

针对文献［12］提出的VSI-EWMAt控制图存在的问题，本文提出VSI-AEWMAt控制图。在Capizzi等［3］提出的AEWMA 控制图的基础上，本文首先给出了AEWMAt控制图的设计方法。结合变采样间隔技术，在AEWMAt控制图中加入警戒线，从而给出了根据统计量的大小调节采样间隔的VSI-AEWMAt控制图。变采样间隔提高了AEWMA 控制图的检测速度，t统计量可以使控制图对方差的估计具有鲁棒性。本文还给出了计算VSI-AEWMAt控制图平均报警时间ATS的Markov链方法，在此基础上提出一种VSI-AEWMAt控制图的参数优化算法。基于该优化算法，计算了特定采样大小下的控制图最优设计参数。最后，以ATS作为指标，评价了VSI-AEWMAt控制图与VSI-EWMAt控制图的性能，结果表明相同情况下VSI-AEWMAt控制图具有更小的ATS。

1 AEWMAt控制图

假设｛Xi，1，Xi，2，…，Xi，n｝来自 同一正 态分布 的总体，其中i=1，2，…表示采样时刻，n表示每个样本的大小。Xij～N（μ0+aσ0，，i=1，2，…，1≤j≤n，其中μ0 和分别为正态分布的均值和方差。a=0，b=1时过程处于受控状态，其他情况表明过程出现了异常。每个采样时刻样本均值和标准差Si分别为：

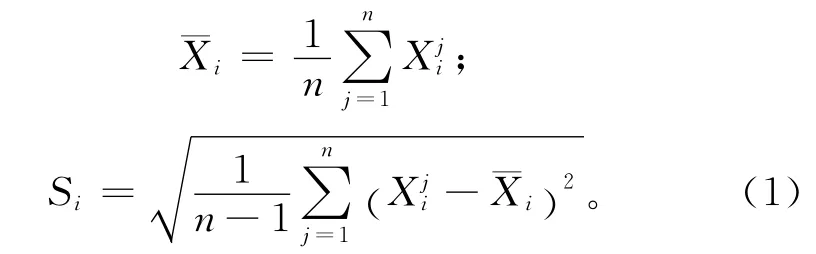
过程受控时，通过式（1）中的两项可以构造一个服从t分布的统计量Ti，

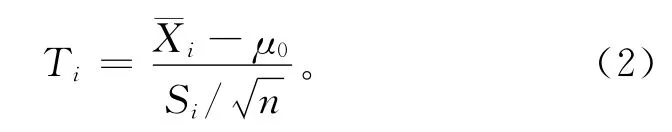
Zhang［9］证明了当a≠0或者b≠1时，Ti服从非中心t分布，

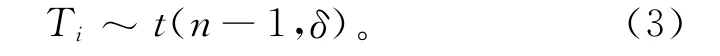
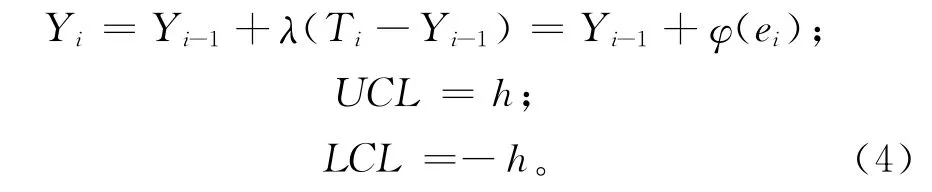
式中：Yi表示第i时刻的AEWMA 统计量，λ为平滑系数，ei=Ti-Yi-1，φ（ei）为估计问题中的误差项。令ω（ei）=φ（ei）／ei，UCL和LCL分别为上下控制限。通过整理，式（4）可重写为

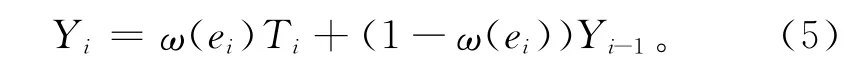
由式（5）可知，ω（ei）作为等效的平滑系数，可根据误差ei的变化而变化，从而实现EWMA 算法的自适应。本文取φ（ei）为如下形式：

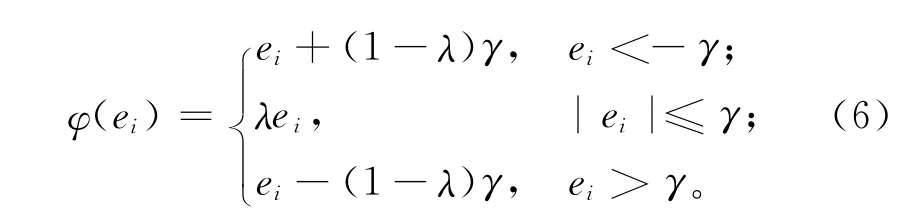
式中γ为一个阈值，当控制图设计完成后γ为常数。

统计量Ti方差的大小只与样本大小n有关，第一阶段的方差估计准确与否并不影响受控状态下统计量Ti的分布形式。

2 VSI-AEWMAt控制图

因为采用式（6）的自适应算法在偏移加大时可以采用更大的平滑系数，所以AEWMA 控制图可以提高EWMA 控制图对大偏移的检测能力。然而，固定采样间隔（Fixed Sampling Interval，FSI）AEWMAt控制图在异常发生时仍不能及时报警，导致生产损失加大，变采样间隔技术可以有效解决这一问题。

2.1 VSI-AEWMAt控制图构造

变采样间隔控制图是在固定采样间隔控制图的基础上加入上下两条警戒线（warning line），当监测变量落在警戒线以内时采用大的采样间隔，反之采用小的采样间隔。设定AEWMA 的上警戒线UWL=ρ和下警戒线LWL=-ρ，则VSI-AEWMAt控制图的工作原理如下：

（1）当被监测变量落在警戒线之间，即-ρ≤Yi≤ρ时，VSI-AEWMAt控制图采用大的采样间隔hl。

（2）当被监测变量落在警戒线与控制限之间，即LCL≤Yi＜-ρ或ρ＜Yi≤UCL时，采用小的采样间隔hs。

（3）当被监测变量落在控制限以外，即Yi＜LCL或UCL＜Yi时，控制图报警。

2.2 VSI-AEWMAt控制图ATS的计算

平均链长ARL是评价固定采样间隔控制图性能的一项重要指标，但是不适用于变采样间隔控制图，变采样间隔控制图需用ATS来评价其性能。根据文献［13］，VSI-AEWMAt控制图的ATS计算过程如下：

将控制限以内的区间［UCL，LCL］等分为m（m为奇数）个小区间，每个小区间Iu的宽度为D=（UCL-LCL）／m，每个小区间的中心为Su=LCL+（u-0.5）D，u=1，2，…，m。控制限以内的各个状态为转移态，控制限以外的区间为吸收态。当统计量Yi落入某一小区间Iu内时，认为Yi处在状态Su。因此可以求得状态之间的一步转移概率矩阵

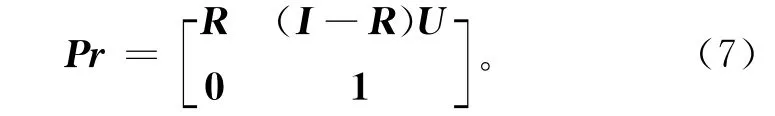
式中：R为一个m×m的实值矩阵，U为一个全1列向量，0为全0行向量。R中的每一个元ruv代表i时刻状态u转移到状态v的概率，由式（4）得

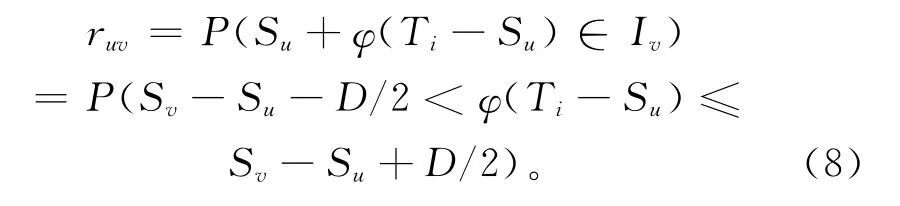
由式（6）可知φ（e）是可逆的，其逆函数为

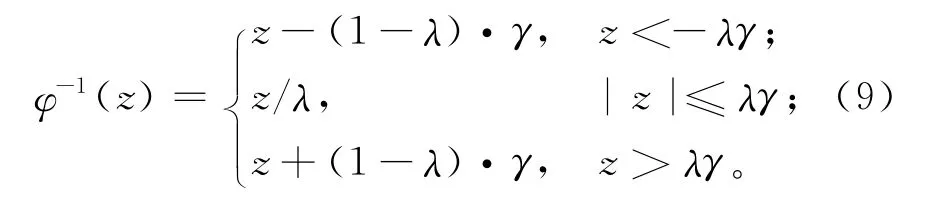
将式（9）代入式（8），可得

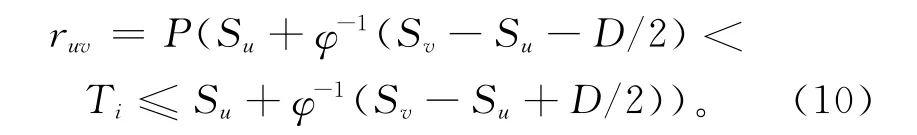
AEWMAt控制图的平均链长可以按照下式求取：

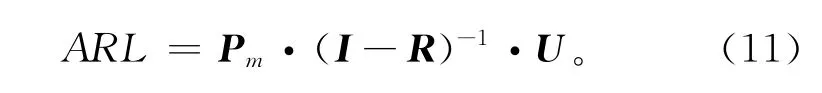
式中Pm为一个1×m的行向量，除了第（m+1）／2个元为1外其他均为0。

ARL的精度与m的选取有很大关系，m越大，ARL的精度越高。当m达到一定值时再增大m对提高ARL计算精度的作用不大，本文选择m=151。

VSI-AEWMAt控制图ATS的计算与平均链长的计算类似，只需将式（11）的ARL计算公式稍作修改即可，VSI-AEWMAt控制图的ATS可以按照下式来求取：

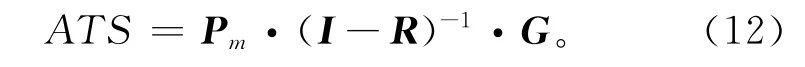
式中G为一个m×1的列向量，其元素由采样间隔hl与hs组成。G中元素gu的取值规则为，当统计量落入警戒线内时采用大的采样间隔，反之采用小的采样间隔。又因为统计量的状态由Su表征，所以有：

（1）当统计量Su包含在警戒线以内，即Su∈［UWL，LWL］时，gu=hl。

（2）当统计量Su在警戒线以外，即Su∈［-∞，LWL］∪［UWL，∞］时，gu=hs。

3 VSI-AEWMAt控制图参数优化

对于固定采样间隔AEWMAt控制图，平均报警时间ATSFSI是通过其平均链长ARLFSI与固定采样间隔hFSI相乘，即

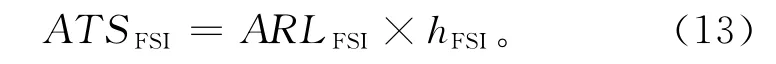
VSI-AEWMAt控制图的平均报警时间ATSVSI求取可等价为平均链长ARLVSI与平均采样间隔E（h）相乘，即

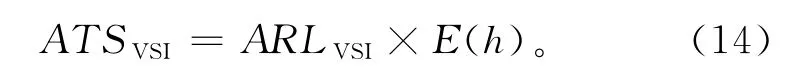
变采样间隔控制图与固定采样间隔控制图作比较的原则是其受控状态下的平均报警时间相等，失控状态下的平均报警时间越短越好。令式（13）中的hFSI=E（h），则可以在相同稳态平均链长指标下比较固定采样间隔控制图与变采样间隔控制图的性能。因此，本文将VSI-AEWMAt控制图的优化分为两个阶段：①优化AEWMAt控制图的ARL，使AEWMAt控制图受控状态平均链长ARL0为固定值，失控状态下的平均链长ARL1尽量小；②求取当前情况下的最优警戒线，使VSIAEWMAt控制图的ATS达到最优。

3.1 VSI-AEWMAt控制图ARL 的优化方法

对于AEWMA 控制图的ARL优化，Capizzi等［3］给出了一种利用分层、加权思想将多目标优化问题转化为两个单目标优化问题的求解算法。Shu［14］则首先将AEWMA 控制图简化为常规EWMA 控制图来处理，求出最优的控制限UCL与平滑系数λ，然后寻找最优的γ。Shu［14］的优化算法相对简单，但是结果的保守性较大。本文采用Capizzi等［3］设计的优化算法，算法描述如下：

（1）选取需要达到的稳态平均链长ARL0，设为B；选取小偏移μ1 与大偏移μ2 的具体值。

（2）针对大偏移μ2 计算参数组合θ1=｛UCL，λ，γ｝，使在ARL0=B前提下失控状态下的平均链长最小。

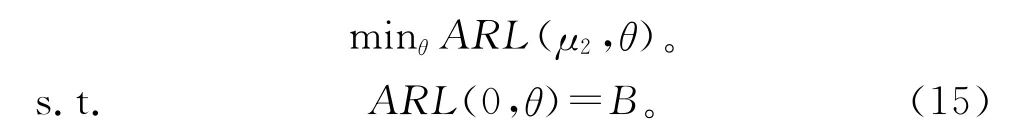
（3）选择一个小的正数α（本文取α=0.05），针对小偏移μ1 优化参数组合θ＊=｛UCL，λ，γ｝，使下式成立：

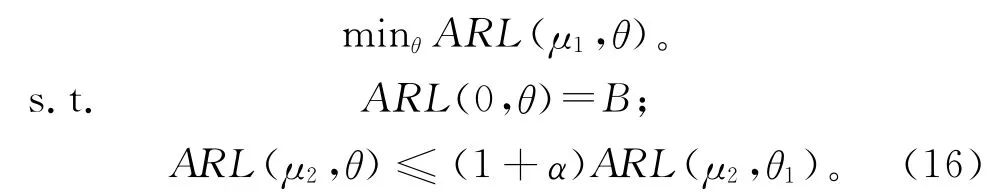
由此得到的参数组合θ＊=｛UCL，λ，γ｝可以保证AEWMAt控制图在小偏移情况下的失控状态平均链长接近最小值，并且在过程出现大偏移时控制图也能具有理想的性能。

对于式（15）和式（16）的求解，Capizzi等［3］使用了200 000次迭代的模拟退火算法，将模拟算法的结果作为Nelder-Mead单纯型法的初值来求取最终结果。这种求解过程需要耗费大量的计算资源和计算时间，结果并非总是最优。粒子群优化算法（Particle Swarm Optimization，PSO）作为一种高效的全局优化算法得到了广泛的关注和研究，传统的PSO 算法性能已经得到了很大提高。本文使用Wang等［15］提出的DNSPSO 算法对式（15）和式（16）进行寻优，该算法在传统PSO 的基础上加入相邻两代粒子之间交叉的多样性促进机制（diversity enhancing mechanism）与邻域搜索策略（neighborhood search strategies），这些改进使DNSPSO 算法能够以更大的概率搜索到全局最优解。相比于Capizzi等［3］采用的模拟退火算法与Nelder-Mead单纯型法相结合的算法，采用DNSPSO 对AEWMA 控制图进行优化可以节省大量计算资源。

3.2 VSI-AEWMAt控制图ATS 的优化方法

在求出VSI-AEWMAt控制图对应的最优设计参数θ＊=｛UCL，λ，γ｝的基础上，对VSI-AEWMAt控制图的ATS进行优化，此时只需求取最优的警戒线ρ即可。

由于该模型下的ATS优化是一个多目标优化问题，常规的ATS优化算法不再适用。类似于AEWMA 控制图ARL优化算法，本文提出一种新的ATS优化算法。在受控状态下平均报警时间ATS0尽量接近其最大值ARL0×hl的前提下，要求失控状态下的平均报警时间尽量小。

结合3.1节的内容，可以得到平均报警时间的优化步骤：

（1）选取需要达到的受控状态平均链长ARL0，设为B；选取小偏移μ1 与大偏移μ2 的具体值。

（2）选择最大采样间隔hl和最小采样间隔hs，根据（1）设定的ARL0得到受控状态下的最大平均报警时间ATS0=B×hl。

（3）针对大偏移μ2 优化警戒线ρ′，取一个接近1的正数η0（本文取η0=0.95），根据3.1节的最优设计参数θ＊=｛UCL，λ，γ｝，使得下式成立：

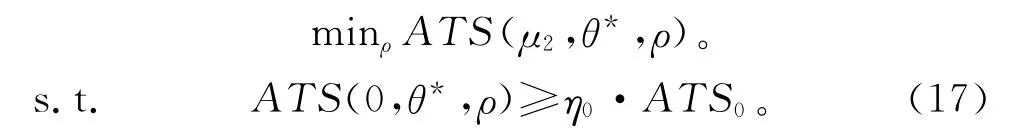
（4）针对小偏移μ1 优化警戒线ρ＊，选取一个接近0的正数η1（本文取η1=0.05），使下式成立：

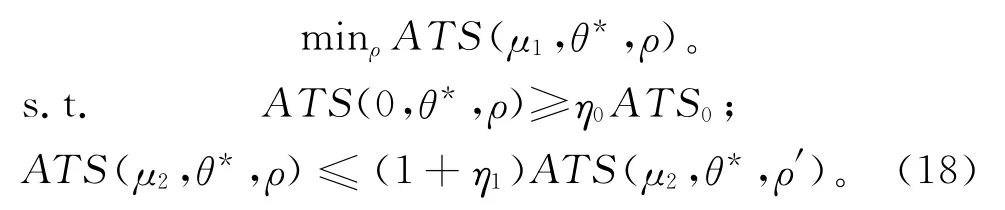
由此得到最优警戒线为ρ＊，即为最终结果。

这种优化方法的优点在于将四维优化问题做降维处理，得到一个三维优化问题与一个一维优化问题，从而大大降低原优化问题的复杂性。求解式（17）和式（18）优化问题的方法与式（15）和式（16）类似，也是通过使用DNSPSO 优化方法求得数值解。

4 仿真研究

对受控状态情况下服从标准正态分布N（0，1）的过程进行仿真研究。选取小偏移μ1 分别为0.25，0.5，1，对应的大偏移μ2 分别为4，5，6。首先，计算样本大小n=5～10时VSI-AEWMAt控制图的最优设计参数λ，h，γ及其对应的ARL，结果如表1所示。

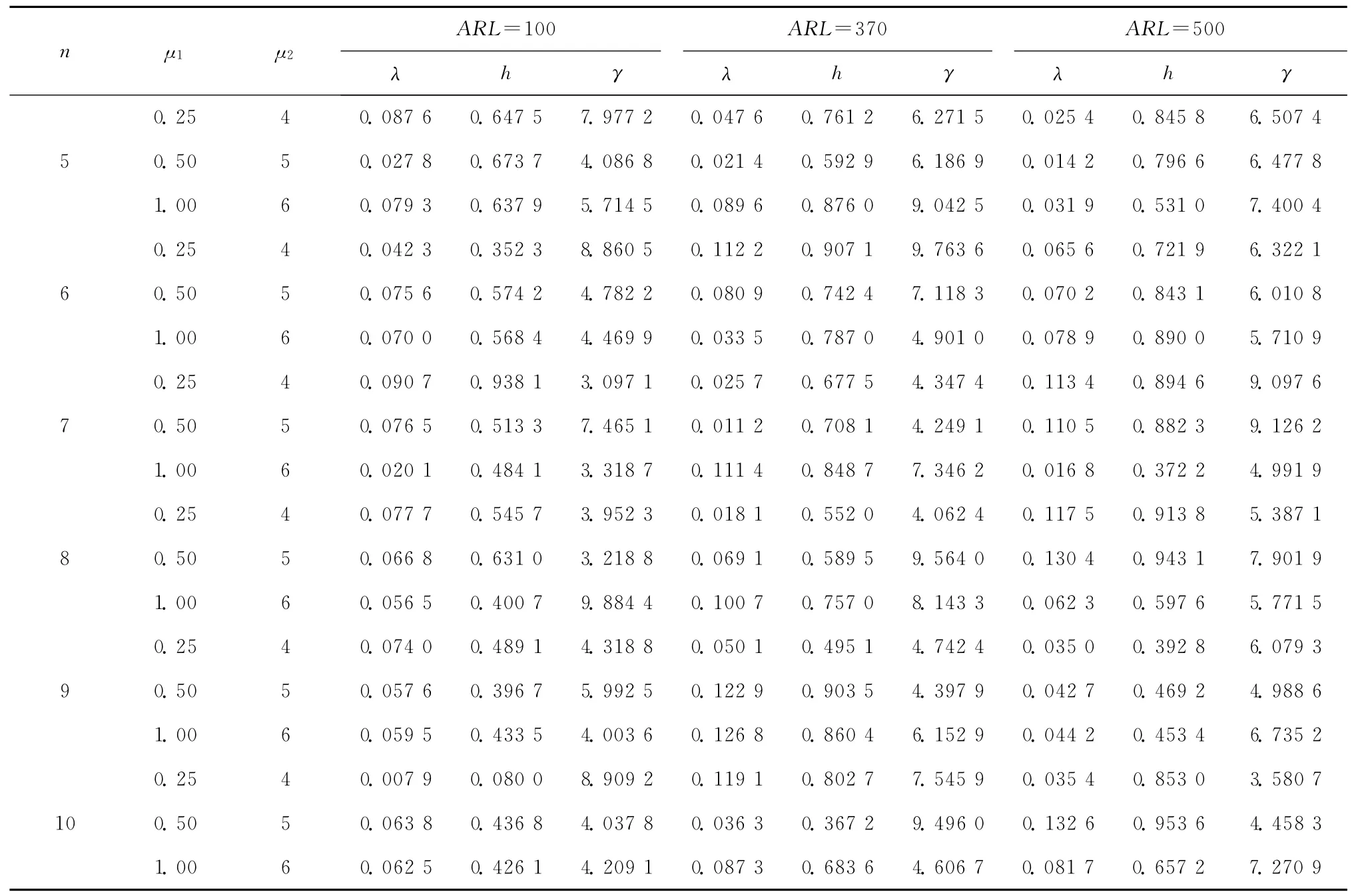
表1 方差估计准确时VSI-AEWMAt控制图的最优参数及对应的ARL

基于表1的结果，计算采样间隔｛hl，hs｝分别为｛2.5，0.2｝，｛2.0，0.2｝，｛1.7，0.3｝时ATS最优警戒线的值，如表2所示。

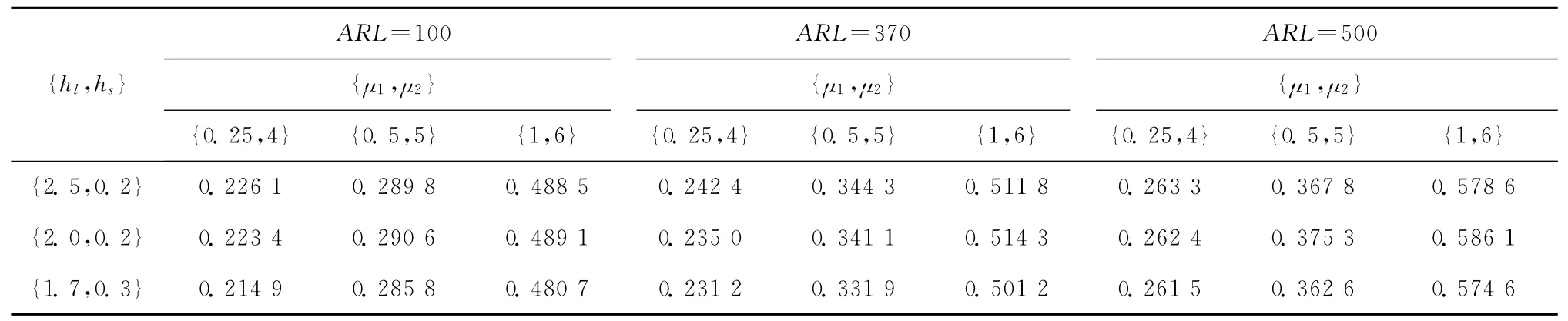
表2 样本大小为5，不同采样采样间隔的下的警戒线

由表2可知，警戒线随着偏移的加大而变大，随着控制限的增加而增加。此外，可以发现警戒线的选取与均值偏离实际值的大小以及稳态ARL的大小有更显著的关系，与采样间隔的关系则不是很明显。警戒线表征了质量特性发生偏移的概率，因此警戒线的取值将受被监测变量的分布形式及分布参数的影响。本文还计算了样本大小n=5、采样间隔｛hl，hs｝为｛2.0，0.2｝和｛1.7，0.3｝时的ATS，结果如表3和表4所示。

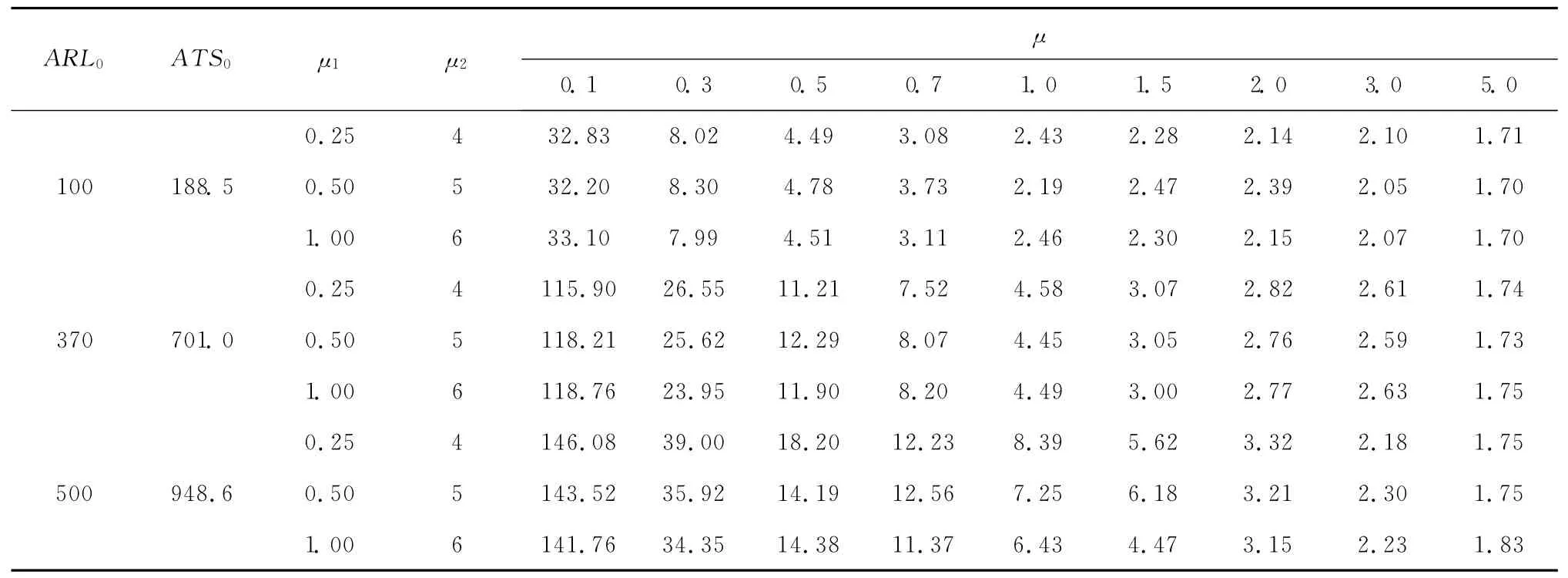
表3 样本大小为5，采样间隔hl＝2.0，hs＝0.2时的ATS

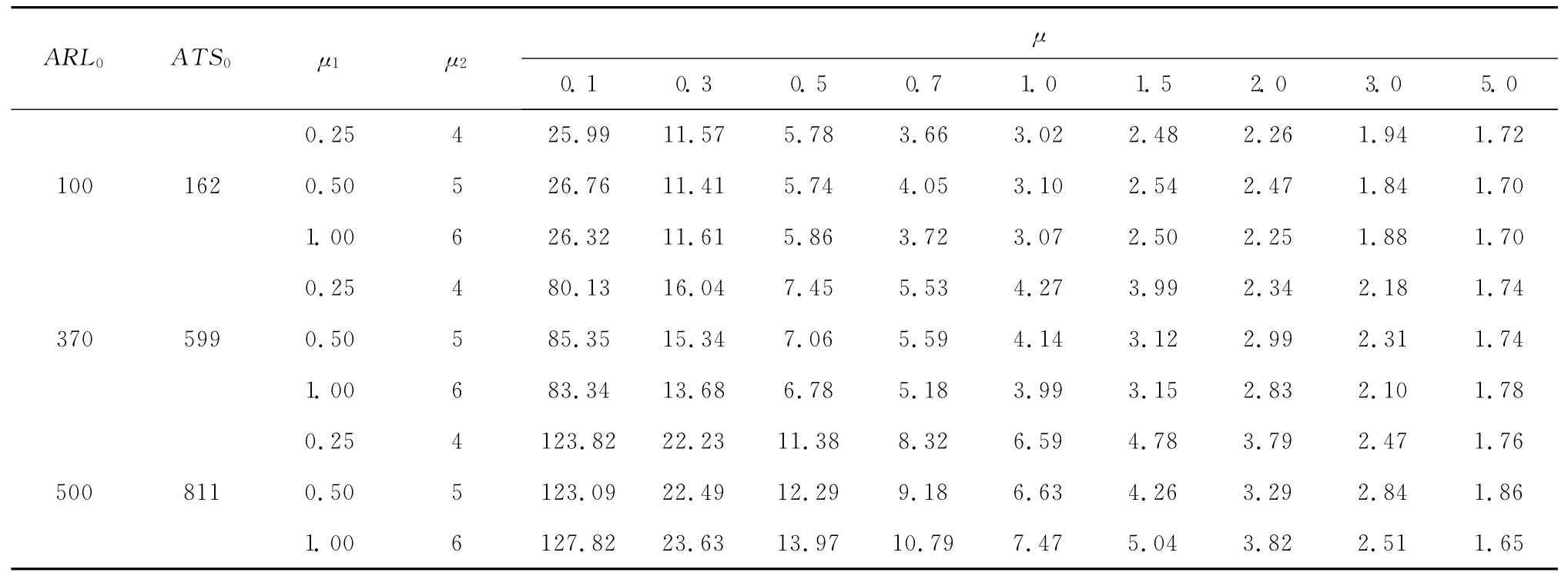
表4 样本大小为5，采样间隔hl＝1.7，hs＝0.3时的ATS

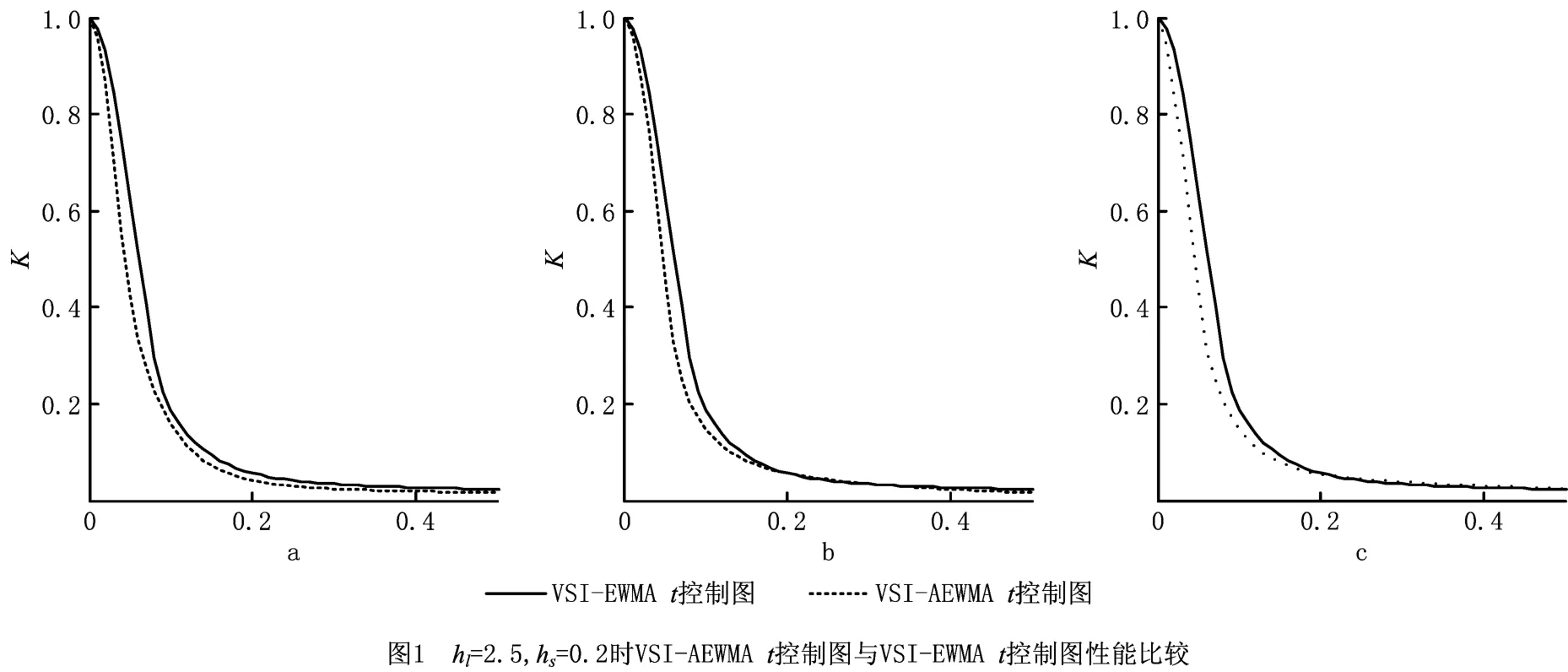
由表3和表4可知，受控状态下ATS达到了最大化的要求，失控状态下的ATS随着偏移的增大迅速减小。选取文献［9］中w=0.3对应的情况，与本文偏移｛μ1，μ2｝=｛0.5，5｝对应的情况进行比较，以失控状态下的平均报警时间ATS1与受控状态下的平均报警时间ATS0的比值K=ATS1／ATS0作为目标，比较结果如图1所示。

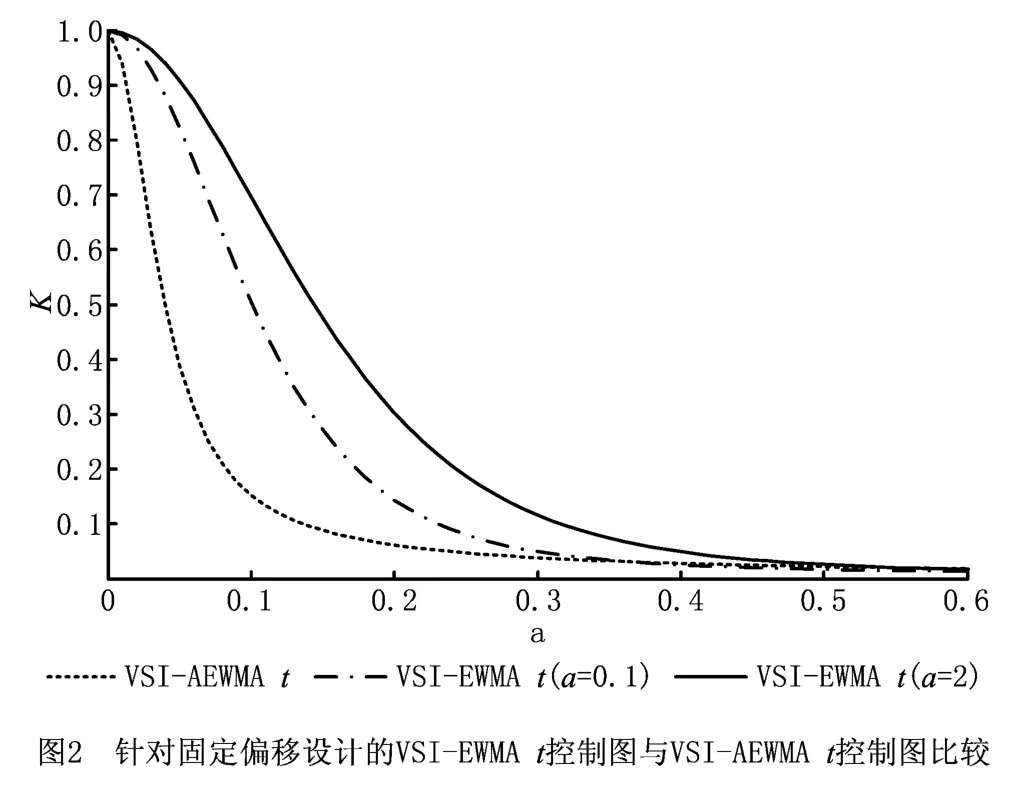
由图1可知，VSI-AEWMAt控制图的性能优于针对不同偏移分别优化的VSI-EWMAt控制图的性能。选取文献［9］中｛hl，hs｝=｛1.7，0.3｝，w=0.3时针对偏移为0.1 与2.0 设计的控制图，与本文｛hl，hs｝=｛1.7，0.3｝，ATS0=599 时，偏 移｛μ1，μ2｝=｛0.25，4｝的情况进行比较，仍然选用失控状态下平均报警时间与受控状态下平均报警时间的比值作为目标，结果如图2所示。

由图2可知，当VSI-EWMAt控制图参数针对固定偏移设计时，会出现对其他偏移不敏感的问题，实际偏移与控制图设计的偏移距离越远，这种不敏感性越明显。而VSI-AEWMAt控制图可以较好地避免这种情况。因此在实际应用中VSI-AEWMAt控制图比VSI-EWMAt控制图更加简便有效。

t控制图对方差估计具有鲁棒性，因此本文研究了b=0.8，0.9，1.0，1.1，1.2 五种 情况下VSIAEWMAt控制图的ATS随a变化的情况。在样本大小n=5，hl=2.0，hs=0.2，μ1=1，μ2=6，ARL=370的情况下进行仿真分析，结果如图3所示。

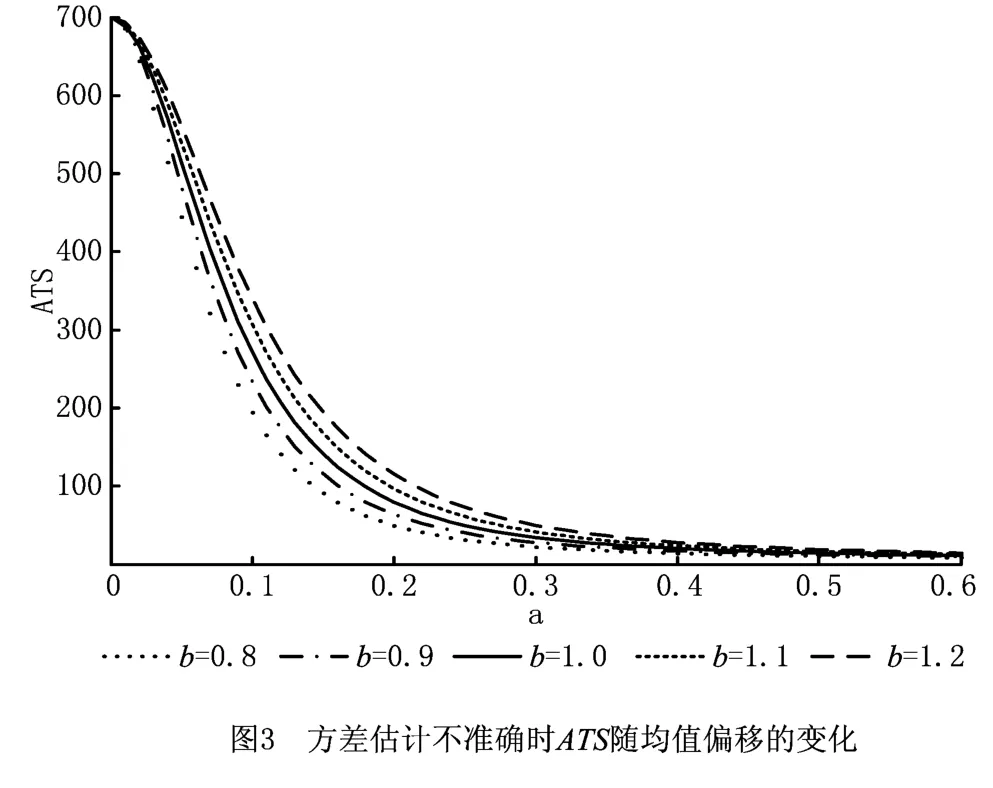
从图3可以看出，方差估计不准确会在a≠0时对t控制图的ATS带来影响，但不会影响到稳态ATS，体现了t控制图具有对方差估计鲁棒性的特点。当方差估计偏小时，会使失控状态下的ATS减小；当方差估计偏大时，会使失控状态下的ATS增大。由非中心参数的表达式可知，这种变化趋势是正确的。

5 结束语

固定平滑系数的EWMAt控制图只对优化设计时所选用的偏移敏感，且异常发生时固定采样间隔不能及时报警。本文针对以上问题构造了VSIAEWMAt控制图，并给出了VSI-AEWMAt控制图ATS计算的Markov链方法；运用多目标优化理论，优化了VSI-AEWMAt控制图的决策参数；以ATS作为评价指标，比较了VSI-AEWMAt控制图与VSI-EWMAt控制图。结果表明，VSI-AEWMAt控制图可以在不损失小偏移检测能力的前提下提高对大偏移的检测能力，且VSI特性明显缩短了失控状态下的平均报警时间。

同时，VSI-AEWMAt控制图的优化过程比较复杂，如何提高优化算法的有效性与减小结果的保守性值得进一步研究。另外，VSI-AEWMAt控制图的经济设计也是值得下一步研究的课题。

［1］ROBERTS S W.Control chart tests based on geometric moving averages［J］.Technometrics，1959，3（1）：239-250.

［2］LUCAS J M，SACCUCCI M S.Exponentially weighted moving average control schemes：properties and enhancements［J］.Technometrics，1990，32（1）：1-12.

［3］CAPIZZI G，MASAROTTO G.An adaptive exponentially weighted moving average control chart［J］.Technometics，2003，45（3）：199-207.

［4］WOODALL W H，MAHMOUND A M.The inertial properties of quality control charts［J］.Technometric，2005，47（4）：425-436.

［5］SACCUCCI M S，AMIN R W，LUCAS J M.Exponentially weighted moving average control schemes with variable sampling intervals［J］.Communications in Statistics-Simulation and Computation，1992，21（3）：627-657.

［6］LEE M H，KHOO M B C.Design of a multivariable exponentially weighted moving average control chart with variable sampling intervals［J］.Computational Statistics，2014，29（1／2）：189-214.

［7］XUE Li.Economic design of variable sampling intervals EWMA chart for monitoring process mean and standard deviation［J］.Computer Integrated Manufacturing Systems，2013，19（6）：1369-1376（in Chinese）.［薛 丽.监控均值标准差的可变抽样区间EWMA 图经济设计［J］.计算机集成制造系统，2013，19（6）：1369-1376.］

［8］HU Xuelong，SUN Jinsheng.Economic design of X control chart with supplementary samples［J］.Computer Integrated Manufacturing Systems，2015，21（1）：160-168（in Chinese）.［胡雪龙，孙金生.带有辅助样本的X 控制图经济设计［J］.计算机集成制造系统，2015，21（1）：160-168.］

［9］ZHANG L，CHEN G，CASTAGLIOLA P.On t and EWMA t charts for monitoring changes in the process mean［J］.Quality and Reliability Engineering International，2009，25（8）：933-945.

［10］CELANO G，CASTAGLIOLA P，TROVATO E，et al.The economic performance of the shewhart t chart［J］.Quality and Reliability Engineering International，2012，28（2）：159-180.

［11］CASTAGLIOLA P，CELANO G，FICHERA S，et al.The variable sample size t control chart for monitoring short production runs［J］.The International Journal of Advanced Manufacturing Technology，2013，66（9-12）：1353-1366.

［12］KAZEMZADEH R B，KARBASIAN M，BABAKHANI M A.An EWMA t chart with variable sampling intervals for monitoring the process mean［J］.The International Journal of Advanced Manufacturing Technology，2013，66（1-4）：125-139.

［13］REYNOLDS M R Jr，AMIN R W，AMOLD J C.CUSUM chart with variable sampling intervals［J］.Techmometrics，1990，32（4）：371-384.

［14］SHU L.An adaptive exponentially weighted moving average control chart for monitoring process variances［J］.Journal of Statistical Computation and Simulation，2008，78（4）：367-384.

［15］WANG H，SUN H，LI C H，et al.Diversity enhanced particle swarm optimization with neighborhood search［J］.Information Sciences，2013，223：119-135.