面向不确定性的再制造车间设施动态布局方法

李聪波，马辉杰，李玲玲，杜彦斌，穆安勇

（1.重庆大学 机械传动国家重点实验室，重庆 400030；2.重庆工商大学 制造装备机构设计与控制重庆市重点实验室，重庆 400067；3.重庆机床（集团）有限责任公司，重庆 400055）

0 引言

进入21世纪以来，资源和环境问题日益严峻，随着相关法律法规的出台和企业环保责任意识的增强，再制造越来越受到重视。再制造是将废旧产品制造成为“如新产品一样好”的再循环过程［1］。由于其蕴含巨大的经济和环保效益，越来越多的制造企业开始涉足废旧产品的再制造工程，如柯达、宝马、惠普、施乐公司等均对其寿命终期产品实施再制造工程并获得了巨大利润［2］。再制造作为一种实现可持续发展的有效手段，在世界各国得到了积极的推广和应用。

然而，再制造系统存在众多不确定性因素［3］，如废旧产品回收的数量和时间的不确定性、废旧产品质量状况不确定性导致的再制造工艺路线和工艺时间的不确定性等，大大增加了再制造车间设施优化布局的难度与复杂性。在实际再制造工艺过程中，废旧零部件在回收时间和数量、再制造工艺路线和工艺时间上的不确定性，导致各再制造工艺单元承担的任务量具有随机性，进而导致各再制造工艺单元的生产设备台数、各个再制造工艺单元之间的物流运输量具有高度不确定性。因此，如何综合考虑再制造系统的众多不确定性因素，以最大化提升再制造车间的物流效率为目标，开展再制造车间的设施优化布局，是一个亟需解决的问题。

车间设施布局是生产制造企业设施规划的一个重要问题。通过对车间中的机器设备、仓库等物流要素进行合理布置，可有效提高物料处理效率、减少在制品停留时间、减少生产提前期［4］。目前关于生产车间设施布局的研究主要分为静态布局和动态布局。静态布局主要考虑生产车间布局相关输入信息（如各工艺间的物流运输量、产品的市场需求等）的不变性。例如：Chan等研究了一个生产多类型产品的制造车间布局问题，通过对所有机器设备进行集群和分群式优化布局，最大程度地减少了产品在各设备群单元内部的物流运输成本［5］；Chaieb等考虑多种物流运输设备、加工工艺顺序柔性等因素，研究了一个圆周型双向设施优化布局问题［6］。然而，由于实际制造系统往往存在一些变动，众多学者更倾向于研究基于多个时段的车间动态布局方法。例如：Dharmalingam 等考虑市场需求不确定性，研究了一个批量生产的自动化车间设施动态布局方法；假设每个工艺单元的大小固定，且每个工艺单元只能容纳一定数量的机器设备；通过优化确定各机器设备在各工艺单元中的位置，最大程度地减少工艺单元内部的物流运输距离［7］。Baykasoglu 等假设车间各工艺单元的尺寸大小相同，综合考虑物流成本和工艺单元重布置成本，建立了车间动态布局优化模型［8］。Mackendall等考虑工艺单元大小的不一致性、工艺单元的朝向随机性等特征，研究了一个开放式的车间优化布局问题［9］。Kia等综合考虑工艺路线可选性、机器设备的生产能力约束、工艺单元大小一致性等特征，研究了一种分批量式生产制造车间的多目标优化布局方法［10］。

由于再制造工艺过程的众多不确定性，使得再制造车间的设施布局比传统的制造车间布局问题更为复杂。如各再制造工艺单元的生产能力需求不确定性，导致再制造生产设备数量随机变动，进而导致再制造工艺单元的尺寸大小也各不相同；此外，废旧零部件再制造工艺路线的随机性，导致各再制造工艺单元间的废旧零部件物流运输量也具有不确定性。因此，亟需开展再制造车间的设施动态布局方法研究。

本文将综合考虑废旧产品回收时间和数量不确定性、再制造工艺路线随机性、再制造工艺的生产能力需求不确定性等因素，开展再制造车间设施优化布局研究。首先对再制造工艺过程的不确定性进行描述，在此基础上对再制造车间的不确定性物流要素进行分析，建立再制造车间设施动态布局模型，并提出一种基于模拟退火（Simulated Annealing，SA）算法的再制造车间设施布局优化求解方法。

1 再制造车间布局不确定性描述

再制造布局问题的相关参数描述如下：

i，j为工艺作业单元序号（i，j=1，2，…，Z），Z表示再制造车间的工艺单元总数，i=1表示拆解工艺单元，i=2表示清洗工艺单元，i=3表示检测工艺单元，i=16表示再装配工艺单元，i=4，5，…，Z-1表示各再制造修复工艺单元；

k为废旧零部件的类型，k=1，2，…，K；

r为再制造工艺路线编号，r=1，2，…，R；

f为再制造车间的行，f=1，2，…，F，F为再制造车间的总行数；

h为再制造车间每一行中定位区域的序号，h=1，2，…，H，H表示再制造车间每一行中的定位区域总数；

t为再制造布局时期的序号，t=1，2，…，T，T表示布局时期总数；

Mli为第i个工艺作业单元中的单台设备长度，Mwi为第i个工艺作业单元中的单台设备宽度，Mli≥Mwi；

Sl为再制造车间的长度，Sw为再制造车间的宽度，Sl≥Sw；

ε为车间主干道的宽度；

δi为第i个再制造工艺单元的重布置成本；

θ为单位物流运输成本；

Δt为第t个布局时期的总物流成本；

Ct为第t个布局时期的工艺单元重布置成本的预算；

βit为一个二进制变量，若第i个再制造工艺单元中的设备竖向排列则βit=1，如果横向排列则βit=0；

πihft为一个二进制变量，若在第t个布局时期内第h行第f列的定位区域被第i个再制造工艺单元占用为第一个定位区域，则πihft=1，否则πihft=0；

（xit，yit）为第t个布局时期的第i个再制造工艺单元的重心坐标。

1.1 再制造工艺过程不确定性

废旧产品的使用寿命因其在服役环境、使用情况、自身物理性质等方面的差异而各不相同，从而导致回收进入再制造系统的废旧产品的数量和时间具有高度不确定性。众多学者在处理废旧产品回收不确定性时，认为废旧产品的回收满足泊松过程［11-13］。

废旧零部件质量状况的差异性导致再制造工艺路线和工艺时间具有高度不确定性。废旧零部件进入再制造系统后，首先经过拆解工艺得到多个废旧零部件，经过清洗和损伤检测工艺后，再根据其损伤状况分为直接重用、可再制造和材料回收三类。可再制造的零部件需要经过一系列再制造修复工艺才能达到新产品的标准。由于废旧零部件在其类型、物理特性、损伤形式和损伤程度等方面的差异，导致其再制造工艺路线具有不确定性。如某废旧机床的关键零部件（主轴、导轨、蜗轮副、丝杠和齿轮等），根据其损伤状况的不同采取的再制造修复工艺也各不相同，具体如图1所示。

由于废旧零部件到达时间和数量的不确定性以及再制造工艺路线和工艺时间的不确定性，导致各个再制造工艺单元承担的任务量也存在不确定性，进而导致各个再制造工艺单元对生产能力的需求不确定，为完成再制造生产任务所需配备的设备数量随机变化。

1.2 再制造工艺过程不确定性建模

（1）废旧产品的到达

众多学者在处理废旧产品到达时间和数量不确定性时，均假设废旧产品的到达满足泊松过程［11-13］。定义一个随机二进制变量Aet表示废旧产品的到达不确定性。若第e个废旧产品在时间段t内到达再制造车间，则Aet=1，否则Aet=0。因此，在第t个时间段内到达再制造车间的废旧产品总数满足。其中：u（x）表示时刻x到达再制造车间的废旧产品数量，满足u（x）～P（λ），λ表示平均到达数量；Bt和Dt分别表示第t个布局时期的开始时刻和结束时刻。

（2）废旧零部件的可再制造性

定义一个随机二进制变量πek，若πek=1则表示第e个废旧产品的第k类废旧零部件可开展再制造加工；否则，该零部件为直接重用或材料回收。各废旧零部件的可再制造性由一个随机概率值确定。

（3）废旧零部件的再制造工艺路线

废旧零部件质量状况的不确定性导致其再制造工艺路线具有高度不确定性。因此，采用工艺概率这一指标描述废旧零部件再制造工艺路线的随机特性［3］。令Pekr为一个随机二进制变量。若Pekr=1，则表示第e个废旧产品的第k类零部件选择了第r条工艺路线；否则Pekr=0。各废旧零部件所选择的工艺路线由一个随机概率值确定。

（4）废旧零部件的再制造工艺时间

废旧零部件的再制造工艺时间因受其质量状况影响而存在较大波动，众多学者将废旧零部件的再制造工艺时间作指数分布处理［11-14］。因此，定义ψki表示第k类零部件在第i个再制造工艺单元中的工艺时间，满足ψki～Γ（1，ν）。其中：1／ν表示期望工艺时间，（1／ν）2表示方差。

1.3 再制造车间布局不确定性

再制造工艺过程的众多不确定性因素，不仅影响各再制造工艺单元设备台数的优化配置，还会导致各再制造工艺单元间废旧零部件物流运输路线和物流运输量的不确定性。具体建模分析如下：

（1）各再制造工艺单元的设备数量

在第t个布局时期中第i个再制造工艺单元所拥有的设备数量Nit，与在该时间段内到达该工艺单元加工的零部件数量、再制造工艺时间（ψki）、单台设备的加工容量（ci）和设备故障率（）有关：

式中：ci表示第i个再制造工艺单元的单台设备加工容量（单位：h／d）表示再制造设备故障率；αir为一个二进制变量，若第i个工艺作业单元存在于第r条再制造工艺路线中，则αir=1，否则αir=0。

（2）再制造车间的物流运输量

废旧零部件在开展再制造加工过程中，需相应地在各再制造工艺单元之间进行物料搬运，由此产生物流运输量。然而，由于废旧产品的到达时间和数量、再制造工艺路线的不确定性，导致各再制造工艺单元间的废旧零部件物流运输量也有高度的不确定性。再制造车间的废旧零部件物流运输量

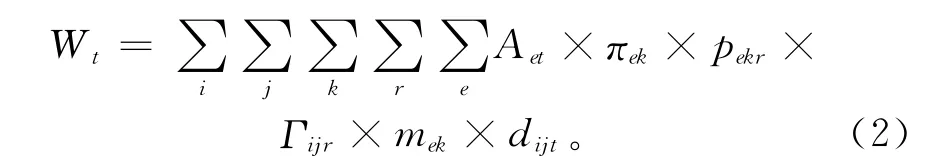
式中：Wt表示在第t个时期的废旧零部件物流运输总量；Γijr为一个二进制变量，Γijr=1 表示零件第r条再制造工艺路线中的第i个再制造工艺紧前于第j个再制造工艺，否则Γijr=0；mek表示从第e个废旧产品上拆解下的第k类废旧零部件的重量；dijt表示在第t个布局时期内第i个再制造工艺单元与第j个再制造工艺单元之间的物流距离。

2 再制造车间设施优化布局模型

2.1 再制造车间布局问题描述

本文研究的再制造车间设施布局问题是基于多个时段（t=1，2，…，T）的车间设施动态布局问题。该问题描述为：一个典型的再制造车间是一个近似矩阵，有固定的长度和宽度；再制造车间中设计有若干条主干道，将再制造车间划分为宽度相等的若干行；再制造车间的每一行中设计有一定数量且长宽相等的定位区域，如图2所示。再制造车间中配备有一系列再制造工艺单元（如拆解、清洗、损伤检测、研磨、车削、电镀铬、激光熔覆、再装配等）；每个再制造工艺单元拥有一定数量的再制造设备，以完成某一相应类型的再制造修复工艺；每个再制造工艺单元根据其所拥有的设备总数量以及单台设备需占用的面积大小，在再制造车间中占用一定数量的定位区域；被同一个工艺单元占用的定位区域必须两两相邻，且不可跨行。

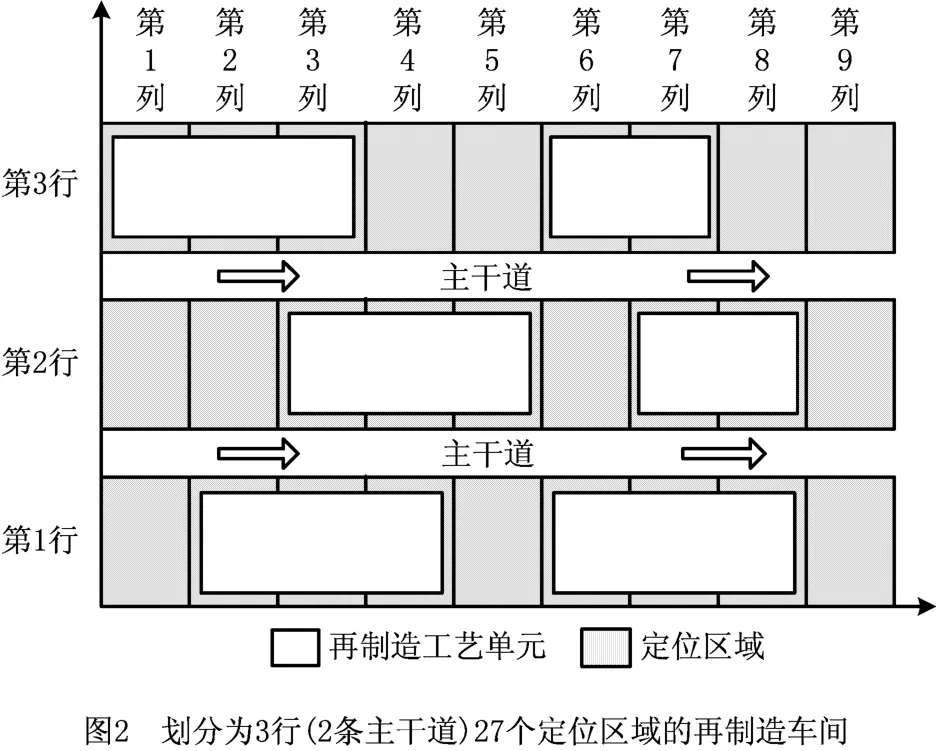
再制造车间布局的假设条件如下：

（1）废旧机床仓库和再制造机床成品仓库分别定位于再制造车间的入口处和出口处。废旧机床回收后首先进入废旧机床仓库，再制造完工后的再制造机床则进入再制造机床成品仓库。

（2）废旧产品的回收时间和数量不确定，其质量状况也不确定，即所选择的再制造工艺路线是随机的。

（3）在各个时间段内，各再制造工艺单元承担的再制造任务量不确定，导致再制造工艺单元对生产能力的需求也不确定，进而导致各再制造工艺单元中的设备数量随机变化。若在一个时间段内某再制造工艺单元的设备数量Nit＜N（it-1），则多余的再制造设备将会被移出原先的定位区域；若Nit＞N（it-1），则新购置的设备将会被放入该再制造工艺单元所占用的定位区域中。这两种情况都会产生工艺单元重布置成本，主要用于设备移除、设备搬迁和设备安装等。

（4）所有再制造设备被看作是近似矩形，其长度和宽度已知。由于各再制造工艺单元因其所拥有的设备数量不同，导致尺寸变动，每个再制造工艺单元根据尺寸大小占用相应数量的定位区域。

（5）各再制造工艺单元中的设备纵向或横向摆放。同一个再制造工艺单元中，所有设备的摆放形式必须相同。

（6）被定位于再制造车间中同一行的所有工艺单元，具有相同的纵坐标。

（7）废旧零部件在各再制造工艺单元内部的物流量忽略不计。

2.2 决策变量

再制造车间动态布局模型的决策变量为：各个布局时期中各再制造工艺单元的设备数量、各再制造工艺单元的尺寸长度，以及各再制造工艺单元在再制造车间中的相对位置。

（1）各再制造工艺单元的设备数量

各再制造工艺单元的设备数量Nit，与时间段t内到达该工艺单元加工的零部件数量、再制造工艺时间、单台设备的加工容量（ci）、设备故障率（）有关，具体计算如式（1）所示。

（2）再制造工艺单元的尺寸

再制造工艺单元的长度受其所拥有的设备数量Nit和设备摆放形式βit影响，具体如式（3）所示。基于再制造工艺单元的尺寸大小可以确定该工艺单元所需的定位区域的数量，如式（4）所示。

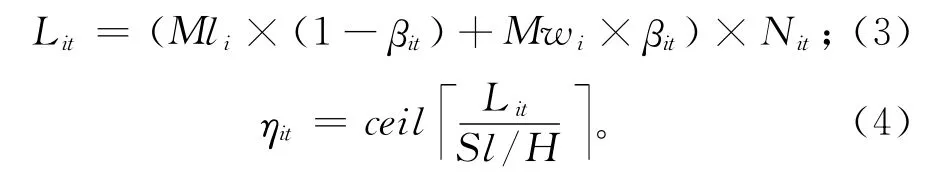
式中：ceil（n）为向右取整函数，即返回大于或等于n的最小整数；Sl／H表示单个布局区域的宽度。

（3）再制造工艺单元的重心坐标

再制造工艺单元的重心坐标表示了该工艺单元在再制造车间中的详细位置坐标，记为（xit，yit）。当各再制造工艺单元在车间中占用确定的定位区域后，其重心坐标可由式（5）计算。基于各再制造工艺单元的重心坐标，可计算出任意两个工艺单元间的物流距离，具体如下：

式中：πihft表示一个二进制变量（决策变量），πihft=1表示第t个布局时期内第h行第f列的定位区域被第i个再制造工艺单元占用，否则πihft=0；Xfh和Yfh分别表示再制造车间中第f行第h列定位区域的横坐标和纵坐标，满足：

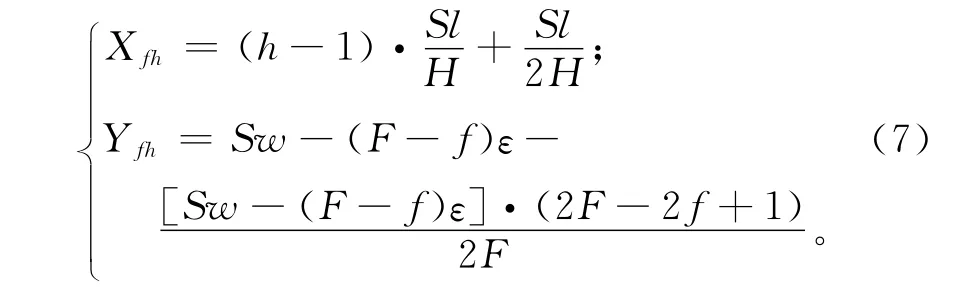
2.3 目标函数

再制造工艺过程的众多不确定性，导致各再制造工艺单元中的设备数量、尺寸大小、物流量情况也不确定。本文以再制造车间的物流成本和工艺单元重布置成本最小为优化目标，具体分析如下：

（1）物流成本

废旧零部件在开展再制造加工的过程中，需相应地在各再制造工艺单元之间进行物料移动，由此产生物流成本。某一布局时期内的再制造车间物流运输总成本

式中θ表示单位物流运输成本。

（2）再制造工艺单元重布置成本

由于各个时段的车间布局方案可能各不相同，在当前时段的布局方案下，需对再制造车间开展重新布局，即调整某些再制造工艺单元的相对位置，由此产生设备移除、设备搬迁和设备安装等费用。

重布置成本由决策变量“再制造工艺单元的重心坐标（xit，yit）”决定，具体计算见式（9）和式（10）。也就是说若重布局方案中某一工艺单元的重心坐标与前一时期的布局重心坐标不一致，则说明工艺单元的位置发生了变动，由此产生重布置成本。式中τit为一个二进制变量。若在第t个布局时期中第i个再制造工艺单元的重心坐标与第t-1个布局时期的重心坐标不同，则τit=1，否则τit=0。

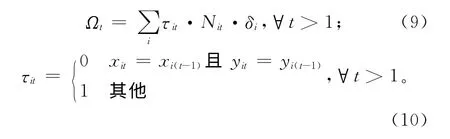
2.4 再制造车间动态布局模型

本文以再制造车间的物流成本和工艺单元重布置成本最小为目标，建立再制造车间设施动态布局模型，如式（11）～式（14）所示。

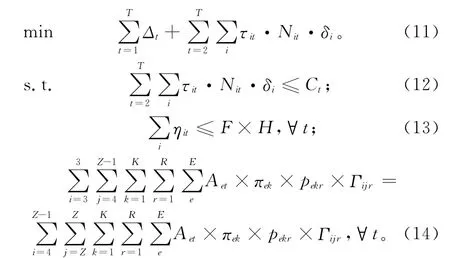
式中：约束条件（12）保证任一时期的再制造工艺重布置成本不能超出该时期的预算；约束条件（13）确保了所有再制造工艺单元占用的定位区域总数不超过再制造车间中所设计的布局区域数量；约束条件（14）是再制造车间的物料流守恒约束，等式左边表示从损伤检测（i=3）进入各个再制造工艺（i=4，5，…，Z-1）的废旧零部件总量，等式右边表示从各个再制造工艺单元完成加工后进入再装配工艺（i=Z）的废旧零部件总量。

3 基于模拟退火算法的再制造设施布局优化求解

SA 算法是一种基于Monte-Carlo迭代求解策略的随机寻优算法。它从某一较高初温出发，伴随温度的不断下降，结合概率突跳特性在解空间中随机寻找全局最优解，即能概率性地跳出局部最优解，最终趋于全局最优［15］。SA 算法因其独特的优化机制以及通用性和灵活性在各领域得到了广泛应用［16-17］。本文引入SA 算法开展再制造设施布局优化求解。

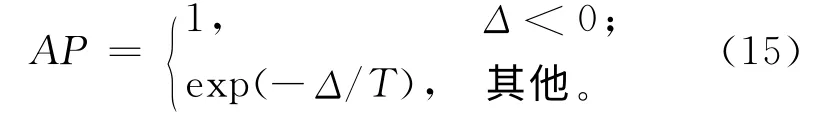
SA 算法首先生成一个再制造布局初始解g0，然后采用某种机制生成一个相邻解g′。如果相邻解g′优于初始解g0，则用g′替换g0；如果相邻解g′并不优于初始解g0，则以一定的概率AP接受相邻解g′并替换g0。接受概率AP的计算方式如下：式中：Δ=f（g′）-f（g）；T表示温度，是一个随迭代次数不断变化的参数；f（g）为优化目标函数。随着每一次SA 算法迭代结束，温度T的被冷却率α减低，由此接受一个劣解的概率也随之降低。当算法满足终止条件时，SA 算法停止运算并输出最优结果。SA 算法是非常成熟的优化算法，本文根据再制造设施布局问题的实际需要，对算法中的关键步骤作了改进，具体如下：

（1）SA 中再制造布局方案解的形式

为了解决再制造设施布局问题中再制造工艺单元尺寸大小不一致的问题，本文设计了一个两阶段矩阵表示再制造设施布局方案。

第一个矩阵A=［atw］T×W是一个初始的再制造布局方案，定义了再制造工艺单元在再制造车间的第一行到最后一行从左到右的排列顺序，其中：W=；atw是一个非负整数，atw＞0表示第t个布局时期内排列在第w个次序的再制造工艺单元编号，atw=0表示排列在第w个次序的再制造工艺单元是一个虚拟的工艺单元，它仅仅会占用1个定位区域（即Nit=1，，Mwi=［SW-（F-1）ε］／F）。图3a所示为4个再制造工艺单元在4个时期内的排列次序。

第二个矩阵E=［etw］T×W与矩阵A对应，定义了在第t个时期内排列在第w个次序的再制造工艺单元的设备摆放形式。其中etw是一个二进制变量0或1。矩阵E需基于矩阵A和各再制造工艺单元的设备摆放形式βit来确定，具体如式（16）所示。当atw＞0时，etw=1表示排列在第w个次序的再制造工艺单元的设备纵向摆放，etw=0表示设备横向摆放；当atw=0 时，表示虚拟单元中的设备纵向摆放，即etw=1。图3b所示为与图3a的矩阵A对应的再制造工艺单元的设备排放形式。

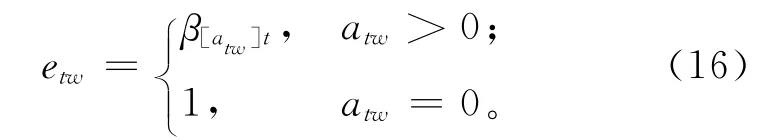
基于矩阵E和式（3）可以确定各再制造工艺单元所需占用的布局区域数量ηit。在此基础上，根据矩阵A可计算出详细的再制造布局方案矩阵G=［gfht］F×H×T，具体算法流程如算法1。在矩阵G中，每一个元素gfht＞0表示在第t个时期中占用了再制造车间第f行第h列的定位区域的再制造工艺单元编号。如果gfht=0，则表示再制造车间第f行第h列的定位区域处于未被占用的状态。图3c所示为基于图3a的矩阵A和图3b的矩阵E计算得到的布局方案矩阵G。

算法1 计算布局方案矩阵G

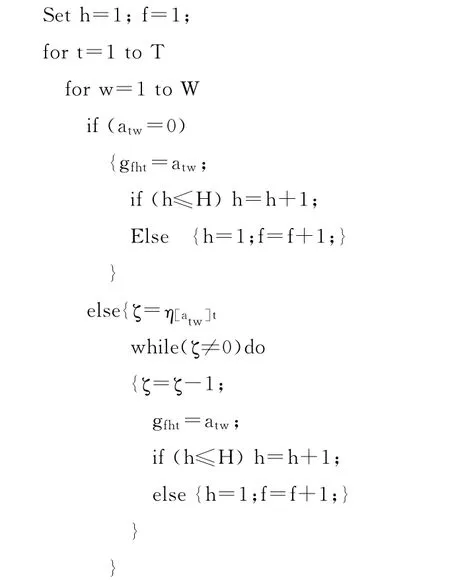
算法1 按照矩阵A中各再制造工艺单元的排列顺序，先后为每一个再制造工艺单元从左到右分配一个或若干个连续的定位区域。为了保证被同一个再制造工艺单元占用的定位区域没有跨行，矩阵G必须满足以下约束：

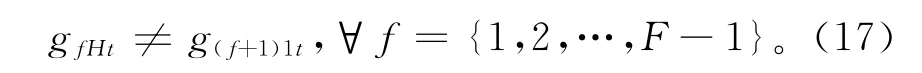
基于一个可行的布局方案矩阵G，通过式（18）计算得到各再制造工艺单元占用的第一个定位单元。在此基础上，根据式（4）～式（11）可以求得再制造布局总成本。

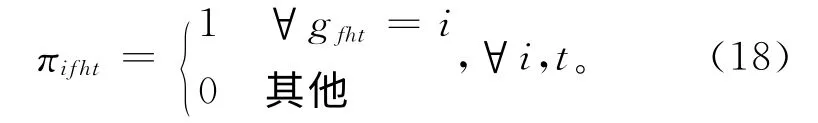
（2）生成SA 算法初始解

初始解质量的优劣对SA 算法的性能影响较大［18］。初始解越差，SA 算法的收敛越慢，产生最优解的质量可能越差。本文生成再制造布局方案初始解的流程如下：

算法2 生成再制造布局初始解。

步骤1 创建两个集合AS和IS。其中：AS=｛（Av，Ev），v=1，2，…，V｝表示再制造布局方案的可行解集合；IS=｛（Au，Eu）｝表示再制造布局方案的非可行解集合。初始化AS=∅，IS=∅。

步骤2 随机产生一个二元组解（A＊，E＊）。如果（A＊，E＊）∉IS且（A＊，E＊）∉AS，则转步骤3；否则，重复步骤2。

步骤3 基于步骤2中的二元组解（A＊，E＊）计算矩阵G。如果矩阵G满足约束条件（17），则更新AS=AS∪（A＊，E＊）；否则更新IS=IS∪（A＊，E＊），重新返回步骤2。

步骤4 如果AS中可行解的数量大于V，则转步骤5，否则返回步骤2。

步骤5 基于式（11），计算AS中所有可行解对应的再制造布局总成本。选择再制造布局总成本最小的二元组解（A＊，E＊）作为SA 算法的再制造布局初始解。

（3）生成SA 相邻解

采用多间隔交换移动方法（ζ间隔，ζ∈｛1，2，…，H-h｝）生成再制造布局方案相邻解［17］，具体算法流程如下：

算法3 生成再制造布局相邻解。

步骤1 任意选择一种间隔方式（m间隔，m∈｛1，2，…，n-w｝），随机选择矩阵A中任意一行t和一列w的元素atw，将atw与at（w+m）相互调换，由此得到一个新矩阵A′；然后随机选择矩阵E中任意一个大于0的元素etw，更新etw=1-etw，得到一个新矩阵E′。由此产生一个新的布局方案相邻解s′=（A′，E′）。

步骤2 基于步骤1生成的相邻解s′计算矩阵G。若矩阵G满足约束条件（17），则输出s′；否则，重新开始步骤1。

（4）算法终止条件

文中SA 算法的终止条件为：①最大的迭代次数olmax已经执行完毕；②连续σmax次的算法迭代过程中，同一个再制造布局方案的最优解没有被更新。

基于SA 求解的再制造布局方案的算法流程如下：

算法4 求解最优再制造布局方案。

步骤1 初始化SA 算法参数：温度T，冷却因子α，外部迭代次数ol=0，内部迭代次数il=0，最大外部迭代次数olmax，最大内部迭代次数ilmax，同一个解没有被更新的最大迭代次数σmax。

步骤2 基于算法2生成一个再制造布局方案初始解s0，令s0l=s0。基于s0l计算再制造布局方案矩阵Gol和相应的布局总成本f（Gol）。

步骤3 While（ol＜olmaxandσ＜σmax）do：

步骤4 输出sol，Gol和f（Gol）。结束算法。

4 案例应用

以某废旧机床再制造车间设施布局为例，对所提模型和方法进行验证。该机床再制造车间共配备16种再制造生产工艺。废旧机床零部件在该车间中的再制造工艺流程如图1所示。为了验证所提出的再制造车间动态布局模型和方法的有效性，本文设计了两个案例：①动态布局，即每4个月对该再制造车间进行重新布局，以一年为期，共开展3次车间优化布局。②静态布局，即以一年为期，对该再制造车间只开展一次优化布局。在静态布局方法中不产生工艺单元重布置成本，只产生物流成本。两个案例均通过MATLAB 2009开展编程和仿真。再制造车间布局的其余参数如表1所示，再制造车间中废旧机床和零部件的相关信息设置如下：

（1）废旧机床零部件每天到达再制造车间的数量满足泊松分布。其中，平均到达数量λ=U［10，15］×v，v∈｛1.0，1.1，1.2，1.3，1.4，1.5｝表示数量扩张因子。

（2）每个废旧机床五类关键零部件的可再制造概率πek=98%。每个可再制造的废旧机床零部件随机产生一种损伤形式，即每个废旧零部件经过各条再制造工艺路线的概率pekr是随机产生的，pekr∈U［0，1］且。

（3）五类关键机床零部件的再制造流程如图1所示。

（4）每种类型的废旧机床零部件的平均工艺时间满足指数分布，即ψki～Γ（1，ν），其中ν∈U［0.05，0.10］。

表1 再制造车间布局的相关参数

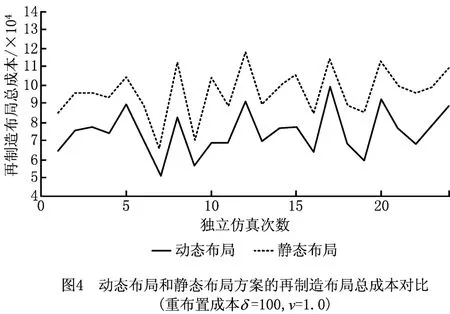
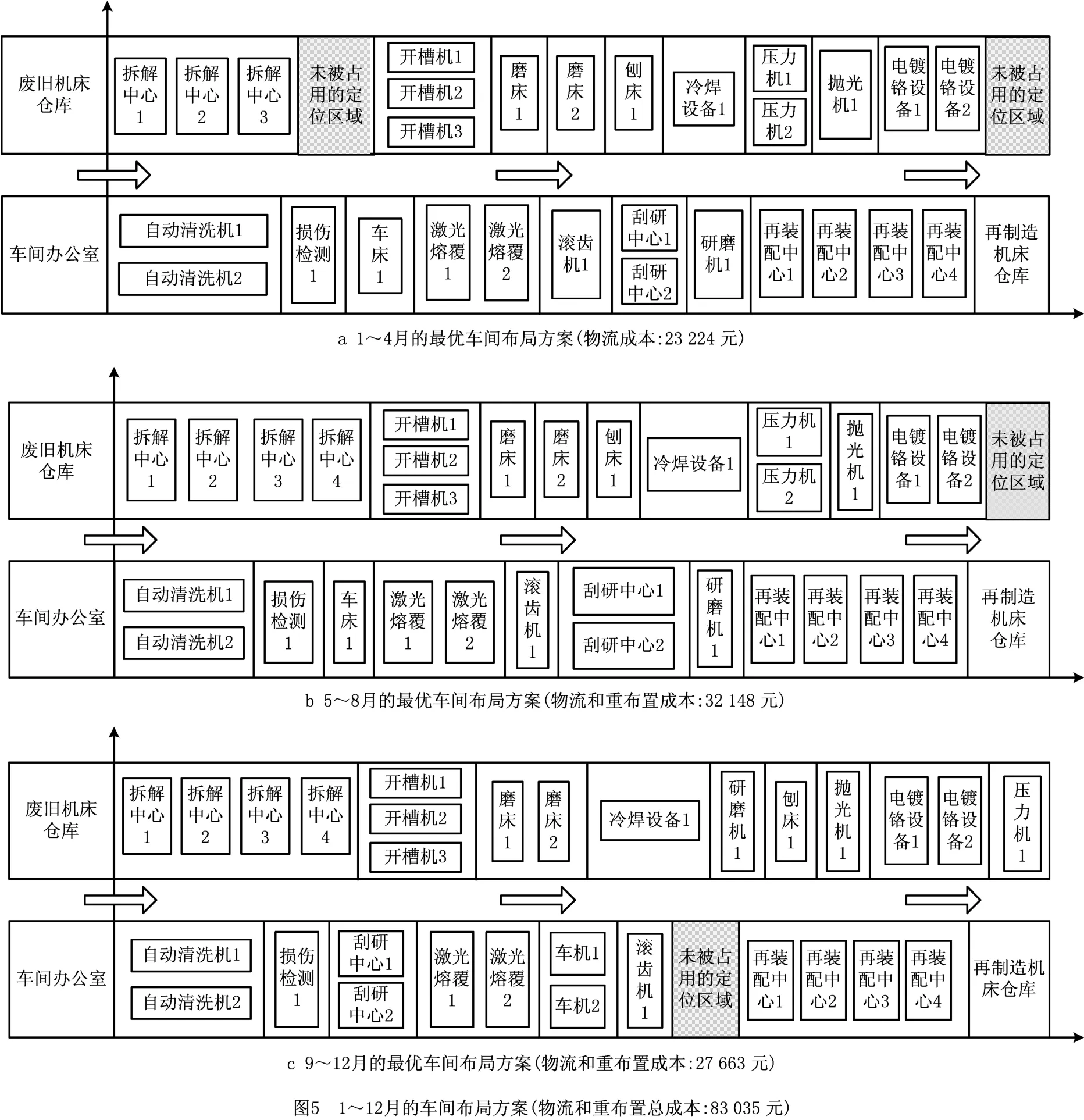
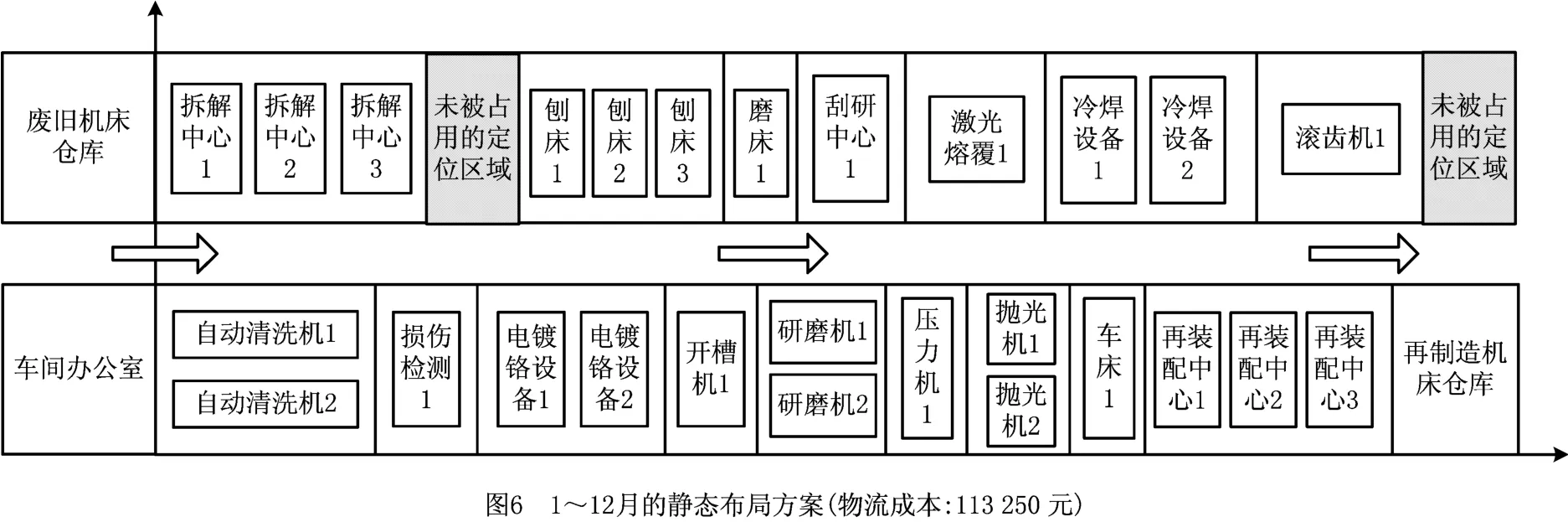
当重布置成本为100时，通过开展24次独立仿真，得到静态布局方案和动态布局方案的再制造布局总成本对比情况如图4所示。其中，动态布局方案下的再制造布局总成本比静态布局方案平均减少23%。图5和图6所示分别为第8次独立仿真得到的最优动态布局方案和静态布局方案。

为了进一步验证动态布局方法的优越性，在不同的平均达到数量下各开展10次独立仿真，统计得到静态布局和动态布局的总成本数据均值，如表2所示。基于表2的数据，对动态布局方案的总成本改善比率（φ1-φ2）／φ1 开展100（1-α）%的置信度区间估计。参数φ的100（1-α）%的置信度区间估计为

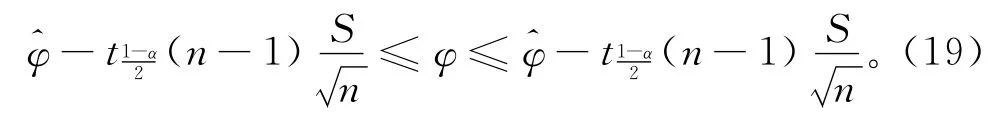
式中：n表示样本容量表示样本均值；S表示样本标 准差）表示自由度为（n-1）的100（1-α）%置信度下的t分布分位数。基于表2的数据，计算得到动态布局方法的总成本改善比率（φ1-φ2）／φ1 的95%置信度区间，如式（20）所示。（φ1-φ2）／φ1＞0，说明在95%的置信度区间估计下，动态布局方法始终优于静态布局。

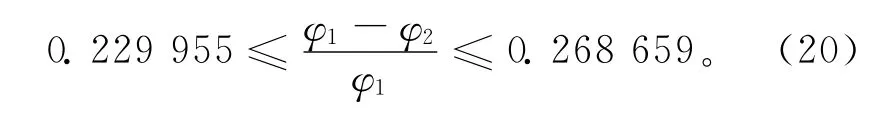
表2 不同平均到达数量下的静态布局和动态布局的总成本均值（重布置成本δ＝100）

在动态布局方法中，通过对再制造工艺单元开展重新布局，即使增加了一部分工艺单元重布置成本，也可减少大部分物流成本。因此，为进一步研究重布置成本的大小对再制造车间动态布局的影响，分别对重布置成本在［100，1 900］区间变动时开展多组独立仿真。图7 所示为重布置成本在［100，1 900］区间变动时动态布局与静态布局的总成本对比情况。由图7可以看出：当重布置成本低于1 200时，通过对再制造工艺单元开展重新布局，可抵消大部分物流成本，使动态布局总成本低于静态布局；然而，随着重布置成本的不断提高，动态布局的优势逐渐丧失，静态布局能取得更低的成本。由此可以说明，对于一个制造车间，若其设施布局的柔性较高，则采用动态布局方法优于静态布局；若该车间的设施不易移动或移动成本非常大，则采用静态布局获得的效果更好。

5 结束语

本文基于废旧产品回收时间和数量不确定性、再制造工艺路线随机性、再制造工艺的生产能力需求不确定性等问题，提出一种再制造车间设施动态优化布局方法。通过对再制造工艺过程的不确定性进行描述，分析了再制造车间的不确定性物流要素，如再制造工艺单元尺寸大小不确定性、再制造工艺单元之间的物流量不确定性，并以再制造物流成本和工艺单元重布置成本最小为目标，建立了再制造车间设施动态布局模型，提出一种基于SA 算法的再制造车间设施布局优化求解方法。最后以某废旧机床再制造车间设施布局为例，运用MATLAB 编程开展优化布局，验证了所提模型与方法的有效性。

由于本文提出了一种再制造车间设施动态布局模型和方法，下一步将研究基于鲁棒性的再制造车间动态布局方法，以提高布局方案对实际再制造系统动态变化的适应性。

［1］XU Binshi.Remanufacturing engineering and its development in China［J］.China Surface Engineering，2010，23（2）：1-6（in Chinese）.［徐滨士.中国再制造工程及其进展［J］.中国表面工程，2010，23（2）：1-6.］

［2］ATASU A，SARVARY M，WASSENHOVE L N V.Remanufacturing as a marketing strategy［J］.Management Science，2008，54（10）：1731-1746.

［3］LI Chengchuan，LI Congbo，CAO Huajun，et al.Uncertain remanufacturing process routings model for used components based on GERT network［J］.Computer Integrated Manufacturing Systems，2012，18（2）：298-305（in Chinese）.［李成川，李聪波，曹华军，等.基于GERT 图的废旧零部件不确定性再制造工艺路线模型［J］.计算机集成制造系统，2012，18（2）：298-305.］

［4］SAHIN R，ERTOGRAL K，TURKBEY O.A simulated annealing heuristic for the dynamic layout problem with budget control［J］.Computer and Industrial Engineering，2010，59（2）：308-313.

［5］CHAN F T S，LAU K W，CHAN P L Y，et al.Two-stage approach for machine-part grouping and cell layout problems［J］.Robotics and Computer Integrated Manufacturing，2006，22（3）：217-238.

［6］CHAIEB I，KORBAA O.Intra-cell machine layout associated with flexible production and transport systems［J］.Proceedings of the Institution of Mechanical Engineers，Part B：Journal of Engineering Manufacture，2003，217（7）：883-897.

［7］DHARMALINGAM P，KANTHAVEL K，SATHIYAMOORTHY R，et al.Optimization of cellular layout under dynamic demand environment by simulated annealing［J］.International Journal of Science Engineering Research，2012，3（10）：91-97.

［8］BAYKASOGLU A，DERELI T，SABUNCU I.An ant colony algorithm for solving budget constrained and unconstrained dynamic facility layout problems［J］.Omega-International Journal of Management System，2006，34（4）：385-396.

［9］MCKENDAL A R，HAKOBYAN A.Heuristics for the dynamic facility layout problem with unequal-area departments［J］.Europe Journal of Operational Research，2010，201（1）：171-182.

［10］KIA R，SHIRAZI H，JAVADIAN N，et al.A multi-objective model for designing agroup layout of a dynamic cellular manufacturing system［J］.International Journal of Industrial Engineering，2013，9（1）：1-14.

［11］GUIDE V D R，SRIVASTAVA R，KRAUS M E.Priority scheduling policies for repair shops［J］.International Journal of Production Research，2000，38（4）：929-950.

［12］CORUM A，VAYVAY O，BAYRAKTAR E.The impact of remanufacturing on total inventory cost and order variance［J］.Journal of Cleaner Production，2014，85：442-452.

［13］TEUNTER R H，FLAPPER S D P.Optimal core acquisition and remanufacturing policies under uncertain core quality fractions［J］.European Journal of Operational Research，2011，210（2）：241-248.

［14］LI Congbo，LI Lingling，CAO Huajun，et al.Fuzzy learning system for uncertain remanufacturing process time of used components［J］.Journal of Mechanical Engineering，2013，49（15）：137-146（in Chinese）.［李聪波，李玲玲，曹华军，等.废旧零部件不确定性再制造工艺时间的模糊学习系统［J］.机械工程学报，2013，49（15）：137-146.］

［15］MOUSAV S M，MOGHADDAM R T.A hybrid simulated annealing algorithm for location and routing scheduling problems with cross-docking in the supply chain［J］.Journal of Manufacturing Systems，2013，32（2）：335-347.

［16］ZHANG R.A simulated annealing-based heuristic algorithm for job shop scheduling to minimize lateness［J］.International Journal of Advanced Robotic Systems，2013，10（1）：1-9.

［17］MANAVIZADEH N，HOSSEINI N S，RABBANI M，et al.A simulated annealing algorithm for a mixed model assembly u-line balancing type-I problem considering human efficiency and Just-In-Time approach［J］.Computer Industrial Engineering，2013，64（2）：669-685.

［18］NASAB N G，AHARI S G，GHZANFARI M.A hybrid simulated annealing based heuristic for solving the locationrouting problem with fuzzy demands［J］.Scientia Iranica，2013，20（3）：919-930.