基于改进GA-RS 的火焰图像特征自适应选择

胡 燕，王慧琴，黄东宇，马宗方

(西安建筑科技大学a.管理学院;b.信息与控制工程学院，西安 710055)

1 概述

火灾的燃烧过程是一个强非线性动力学系统，火灾燃烧状态变化受到可燃物的数量、种类和燃烧区域风速等诸多因素制约，具有很强的模糊及随机特性。现有的在特定条件下人为设定火焰在图像上表现单个或某几个特征信息作为识别依据的算法使得火灾探测算法的推广能力大受影响。对于模式识别，重复和不重要的特征项不但不会提高算法的分类能力，反而会使特征组合的分类能力下降。当输入的特征项增加时，分类器要求的训练样本数量会呈指数关系增长［1］。因此，在对火焰辨识中，有必要强调特征选择的显著性度量，力求在不失可靠性的情况下，简化特征模型和减少冗余计算。

分支定界搜索法、前向/后向序贯和极大-极小选择［2］等是常用的特征选择算法，存在没有把知识与分类有机地联系在一起，难以分析、发现和推理数据间的关系［3］。粗糙集(Rought Set，RS)［4］是1982 年提出的一种处理模糊不确定型的数学算法，核心内容是属性约简，即保持信息系统分类能力不变导出与原始数据具有相同决策能力的最小集合。它无需提供问题所需处理数据集合之外的任何先验信息，对问题的不确定描述或处理是比较客观的，然而求解最小属性约简被证实是一个NP 难题［5］。遗传算法(Genetic Algorithm，GA)是受生物进化论启发而提出的一种基于适者生存机制的随机优化算法，具有较强的全局寻优性能，具有较高的并行处理能力。不少学者将GA应用于解决粗糙集中的属性约简。

这些研究主要集中在改进算法的复杂度和加入启发式信息等方面［6］，为了使寻优结果尽可能逼近最优解，但却不能保证获得的属性子集是最简的。因此，本文结合粗糙集和遗传算法各自的特点，利用粗糙集思想定义遗传算法适应度函数，设计自适应交叉和变异算子，将动态裁剪相似个体和补充新个体的策略引入到种群更新中，增加染色体的多样性，解决传统GA 早熟问题。

2 粗糙集

在粗糙集理论中，对象的知识是通过指定对象的基本特征(属性)和它们的特征值(属性值)来描述的。一个知识表达系统定义为:

定义1 对于属性集P⊂R(R=A∪D)，对象X，Y⊂U，P 上的不可分辨关系为:

定义2 设论域U 上的2 个等价关系簇为P 和Q，Q 的P 正域定义为则称Q以γ 依赖于P(P 以γ 支持于Q)，记为:

(1)当γ=1 时，决策Q 完全由条件P 确定。

(2)当0 ＜γ ＜1 时，决策Q 部分由条件P 确定。

(3)当γ=0 时，决策Q 完全独立于P。

定义3 对于∀c∈C，若c 满足pos{C-c}(D)=pos{C}(D)，则称c 是C 中D 不必要的，否则c 是C 中D 必要的，所有必要的属性构成的子集为C 的一个约简，所有C 的属性约简的交集称为C 的核:

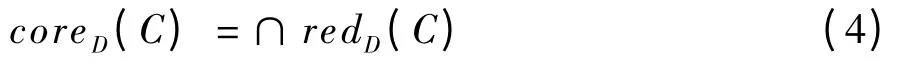
对于核，有:

3 遗传属性约简的特征选择算法

参数编码、初始群体的设定、适应度函数设计、遗传操作和控制参数设定是遗传算法的5 个基本要素，其中，编码、适应度函数和遗传算子的设计是实现整个GA 的关键。将RS 属性约简的思想引入到GA 中，在GA 的每个关键环节融合RS 的设计理念，从而解决火焰图像特征随监控场景变化的自适应选择问题。

3.1 参数编码

遗传算法不能直接处理问题空间的参数，需要通过一定的编码规则把要求问题的可行解表示成遗传空间的染色体或者个体［7］。火焰识别属于二分类问题。在对火焰特征集合进行属性约简之前需要对其进行离散化处理，将特征值转化成0 或1 整数，从数值表型形式上看更接近遗传算法中的二进制编码形式，因此，选用二进制编码算法对火焰图像特征参数进行数值空间转换。具体做法是:采用固定长度的二进制符号串表示种群的个体，等位基因由符号集{0，1}构成，其中，1 表示选择其对应的条件属性;0 表示不选择其对应的条件属性。若1011010100 表示一个长度为10 的个体，则对应选择的属性子集为{a1，a3，a4，a6，a8}。

3.2 适应度函数

适应度函数是评价染色体优劣的唯一确定性标准，决定群体的进化方向。由属性约简的定义可知，适应度函数的设计受2 个因素影响:(1)属性的分类能力:条件属性对决策属性的支持度尽可能大。(2)染色体中含1 的数量:属性的个数尽可能少，这样被选中的概率才会越大。根据上述2 个指标，定义新的适应度函数为:

其中，m 表示条件属性的个数;card(x)表示每个个体中1 的个数;γC(D)表示条件属性集C 对决策属性D的支持度，由定义2 计算可以得到。γC(D)越大说明条件属性与决策属性的相关性越大，在保证约简后得到的属性个数小的同时使属性间的相关性较小。从式(6)可知，个体中所包含条件属性越少，以及条件属性与决策属性的相关性越大，则适应度值越大。

3.3 遗传算子

遗传算子包括选择操作、交叉操作和变异操作。这里选用适应度比例算法(轮盘赌法)进行个体选择，根据每个个体适应度的值从中选择较大者进入新的种群，体现了自然界优胜劣汰的自然法则［8］。个体被选中的概率为:

其中，Fi表示第i 个个体的适应度值;n 表示群体的规模。

交叉操作中的交叉概率pc控制交叉算子的使用频率，使解达到最有希望的全局最优解区域。变异操作中的变异概率pm控制变异算子的使用频率，决定了GA 的局部搜索能力。在标准的GA 中，一般情况下pc和pm是固定的，凭经验选取，其取值直接影响算法的收敛性。过大的pc和pm使GA 退化成随机搜索算法的可能性也越大;pc和pm取值过小，算法容易过早收敛于局部最优解。而适应度值大的个体表明其基因优，在遗传操作中希望其优秀的基因被保留到子代中，因此，可以让pc和pm随适应度值自适应调整。调整公式为:

3.4 动态相似个体裁剪和新个体补充

当群体中的个体非常相似，群体的多样性急剧减少，群体缺乏有效等位基因，在遗传算子作用下不能生成高阶竞争模式，会出现“早熟”现象［9］。通过对邻近个体进行适当的修剪，减少基因的单一性:对每个个体，寻找最近邻，计算2 个个体之间的相似度S(用欧氏距离表示)，S 小于阈值T，认为2 个个体相似，删除适应度值较小者。经裁剪相似个体操作后，种群规模减小，为了保证群体规模，采用最优保持策略［10］添加新的个体，动态地解决了种群因缺乏多样性而陷入局部最优解的问题。

改进的GA-RS 火焰图像特征选择算法流程如图1 所示。

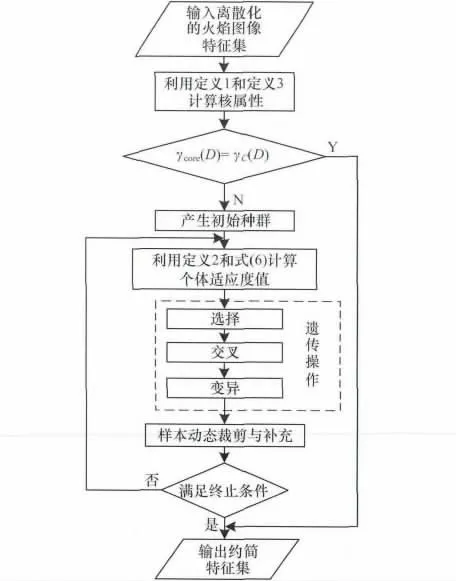
图1 改进的GA-RS 火焰图像特征选择算法流程

4 仿真实验分析

4.1 数据集测试

样本数据是根据国家标准《GB 15631-2008》在大空间环境下白天和夜晚自行拍摄的视频，以庚烷、汽油、煤油、柴油、酒精、汽油与煤油按照10:1 的混合液作为点火材料;打火机火、蜡烛火、探照灯、警灯、手电筒、运动的车灯、环形灯和白炽灯为干扰源，数据集共500 个样本，部分截图如图2 所示。

图2 数据集部分视频截图

4.2 改进的特征选择算法有效性分析

利用火焰图像分割算法提取可疑目标，用c1，c2，c3，c4，c5，c6和有火/无火表示圆形度、尖角数、红绿分量面积比、面积变化率等6 种特征和决策结果，论域U={x1，x2，…，x200}，条件属性C={c1，c2，c3，c4，c5，c6}，决策属性D={d}，当d=1 时表示有火情况，当d=0 时表示无火情况。

通过文献［11］的特征量归类表将6 个特征离散化，将检测数据映射到信息系统，初始参数取值分别为:迭代次数N=100;种群规模n=50;pc1=0.85;pm1=0.1;β=0.7;T=1.8。

分别使用火焰6 个特征和支持向量机(Support Vector Machine，SVM)结合(ALL +SVM)、基于支持向量机的图像型火灾探测算法［12］、粗糙集和SVM结合(RS+SVM)，以及遗传算法、粗糙集、SVM 结合(GA+RS+SVM)的4 种算法对离散化的火灾/干扰数据集进行训练，训练样本是从500 个数据集中分别随机选择100 个有火和干扰样本，再从剩余中选则部分数据作为测试样本，预测结果如表1 所示。

表1 4 种火焰识别算法的实验结果对比

对表1 实验结果分析如下:

(1)样本中特征数量越多并不表示一定能提高识别精度。特征之间的相关性，冗余或不重要特征彼此之间的干扰很容易降低分类准确率。

(2)固定分类特征组合依赖训练样本集，导致识别算法的自适应能力差。但是当训练样本集改变，最有效的特征子集也会发生变化，如果仍然沿用原来的固定3 个特征识别火焰会使算法的识别精度迅速下降。

(3)经特征选择后，特征数目均少于原始特征数目，同时能保持高于原特征集的识别率。RS +SVM 算法特征数目减少2 个，GA +RS +SVM 算法特征数目减少3 个。尽管GA+RS+SVM 算法是4 种算法中最耗时的，识别时间最慢达到16.7 s，与前3 种算法相比，平均会多增加6 s～7 s 的运算时间，但是经过GA 优化后的RS 算法，扩大了最优解的搜索空间，得到的解更加准确，实现了特征的优化组合。另外，总的来说，动态特征对识别率的贡献大于静态特征，主要是因为动态特征受外界干扰影响较小，获取的特征值相对较为稳定。

5 结束语

火焰图像特征选取是否合适直接决定分类器的准确率。为了提高火焰探测精度，使火焰图像特征随监控场景的不同自适应地选择最佳、最小特征组合，本文提出一种基于改进GA-RS 的火焰图像特征选择算法。实验结果表明，该算法不但减少了特征数量，还具有较强的泛化能力。

［1］毛罕平，徐贵力，李萍萍.基于遗传算法的蔬菜缺素叶片图像特征选择研究［J］.江苏大学学报:自然科学版，2003，24(2):1-5.

［2］曾黄麟.粗集理论及其应用［M］.重庆:重庆大学出版社，1998.

［3］赵 勇，方宗德，王侃伟，等.邻域粗糙集在轮对踏面缺陷图像特征选择的应用［J］.计算机测量与控制，2008，16(11):1730-1731，1734.

［4］Pawlak Z.Rough Sets［J］.International Journal of Information and Computer Science，1982，11(5):341-356.

［5］梁 琰，何中市.一种基于粗糙集启发式的特征选择算法［J］.计算机科学，2007，34(6):162-165.

［6］陈 曦，雷 健，傅 明.基于改进遗传算法的粗糙集属性约简算法［J］.计算机工程与设计，2010，31(3):602-604，608.

［7］张 晋，李冬黎，李 平.遗传算法编码机制的比较研究［J］.中国矿业大学学报，2002，31(6):93-96.

［8］边 霞，米 良.遗传算法理论及其应用研究进展［J］.计算机应用研究，2010，27(7):2425-2429，2434.

［9］周洪伟，原锦辉，张来顺.遗传算法“早熟”现象的改进策略［J］.计算机工程，2007，33(19):201-203.

［10］张杰慧，何中市，黄丽琼.基于改进的RS-GA 图像特征选择方法［J］.计算机应用，2006，26(10):2372-2374.

［11］胡 燕，王慧琴，秦薇薇，等.基于粗糙集的火灾图像特征选择与识别［J］.计算机应用，2013，33(3):704-707.

［12］杨娜娟，王慧琴，马宗方.基于支持向量机的图像型火灾探测算法［J］.计算机应用，2010，30(4):1129-1131，1140.