等比力法与等角位置法测试加速度计误差模型系数的比较
王凯强,董春梅,任顺清
(哈尔滨工业大学空间控制与惯性技术中心,黑龙江哈尔滨150080)
0 引言
加速度计作为惯性系统中测量运动载体加速度的重要仪表,对其惯性精度要求很高。为了提高惯性系统的精度,从敏感元件的角度看,一是要继续提高加速度计的制造精度,二是辨识加速度计的误差模型,深入分析和研究加速度计的误差源和误差特性,寻求恰当的方法进行误差补偿,消除或减小误差,提高标定精度。
目前,很多文献介绍了不少标定方法[1~3],但加速度计的误差标定主要还是在重力场上的静态翻滚试验和在精密离心机上的测试试验。加速度计的标定首先需要在精密分度头上进行,尽可能精确地辨识出加速度计的零位偏置KF,标度因子KI以及KO,KP等误差模型系数;在此基础上,再进行加速度计在精密离心机上的标定,确定加速度计的其他高阶误差模型系数。文献[4]对误差标定实验设计优化,消除了转台误差对加速度计的影响。文献[5]在重力场标定情况下通过全组合法辨识加速度计的误差模型系数,消除测试设备角位置误差对测试精度的影响。文献[6]提出正交双表的两种安装位置组合测试法,分离分度头的位置误差,消除角位置误差对加速度误差模型系数的标定结果的影响。文献[7]对加速度计的1 g重力场静态翻滚试验进行谐波分析,得出了加速度计的静态数学模型系数的性能指标;但针对加速度计在重力场上的翻滚测试试验,只介绍了等角位置的翻滚测试,对等比力法的翻滚测试没有具体分析,更没有对两种方法进行比较择优。本文论述了在重力场下的等角位置和等比力旋转测试方法辨识加速度计误差模型系数的两种方法,在辨识误差模型参数的同时,比较两者对加速度计误差模型系数的标定精度的影响,并进行择优选择。
1 测试装置
如图1所示,整个测试系统主要由光栅分度头、加速度计、夹具、数字电压表、电源等组成,其中光栅分度头的角位置分辨力为0.1"。

图1 测试装置
加速度计的安装状态分为摆状态和门状态[5],图1所示的加速度计处于门状态,即加速度计的摆轴始终处于水平状态,并平行于光栅分度头转轴,输入轴I与输出轴O分别绕分度头转轴在铅垂面内旋转。已知加速度计的三个轴分别为输入轴I、输出轴O、摆性轴P,忽略摆性轴的安装误差,可以认为摆性轴的轴向与当地重力加速度g的方向正交,即ap≡0。当分度头旋转到某个角度时,设加速度计输入轴与水平面夹角为θ,重力加速度在加速度计三个轴上的分量为
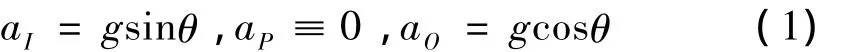
式中:aI,aO,aP为输入轴、输出轴、摆性轴的比力分量。
已知在理想的门状态下,加速度计的静态误差模型为

将公式(1)代入公式(2)中得

式中:U为加速度计输出值,V;KF为零位偏置,V;KI为标度因数,V/g;KO为交叉轴敏感系数,一般由加速度计二维失准角和安装误差引起,V/g;KIO为交叉耦合误差系数,V/g2;KII为二阶非线性误差系数,V/g2;ε为随机误差,V。
2 重力场下等比力法旋转测试
由于加速度计的敏感输入量为重力加速度产生的比力,为了最大限度地增加其对不同比力输入的响应,设想在重力场下尽量可能多的通过不同大小和方向的给定输入,测试其响应情况[6]。为此,设计一种重力场下的等比力旋转测试方案,来辨识加速度计的误差模型系数。
根据公式(4),在重力场下-g~g之间等比力选择20点进行测试,即选取θ1,…,θ20使得比力aI在-0.8 g~+0.8 g,每间隔0.2g各有两次比力输入,而对应-g与g将取唯一的角度θ6,θ16。设计的比力及相应分度头所处的角位置,加速度计的输出U如表1所示。
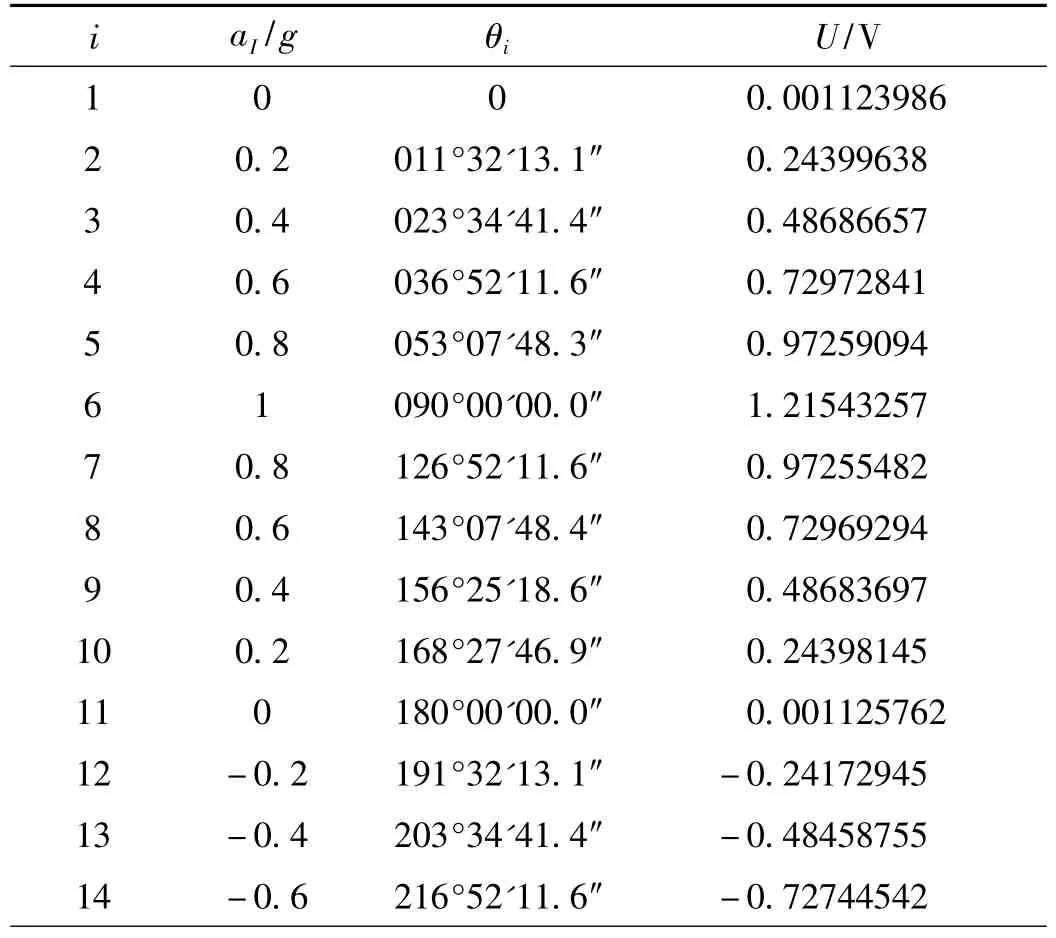
表1 重力场等比力测试数据
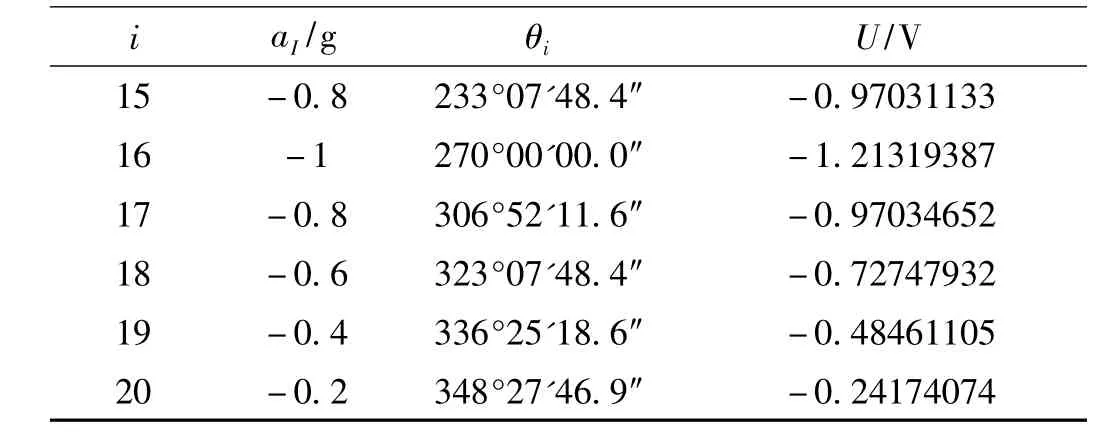
续表
3 重力场下等角位置测试
根据公式(3),与上述的等比力测试方案对应,在重力场下同样选择20点测试实验。即在0~360°之间等角位置选取20点θ1,…,θ20,使θ1=2π(i-1)/20,i=1,2,…,20。加速度计的输出如表2所示。

表2 重力场等角位置测试数据
4 测试误差分析
在加速度计误差模型系数辨识领域中,最小二乘法是最常用的辨识方法[8-9],其基本原理就是根据观测数据推断未知参数,未知参数的最优值可使各项实际观测值与计算值之间差值的平方和最小。
分别将表1和表2中的20个测试点的角度和相应的输出代入公式(3)即可得:
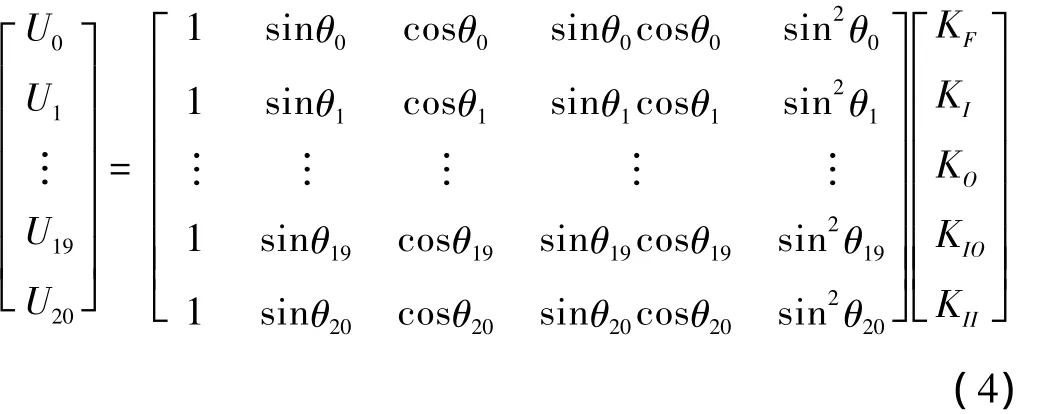
进而将公式(4)写成矩阵形式:

采用最小二乘法就可得到方程K^=(ΦTΦ)-1ΦTU令Q=(ΦTΦ)-1,
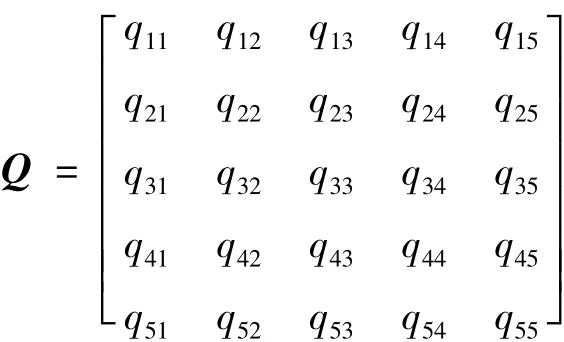
由加速度计误差模型系数的残差方程为
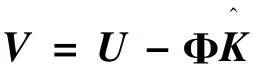
可得到加速度计输出值U的单位权标准差估计值为
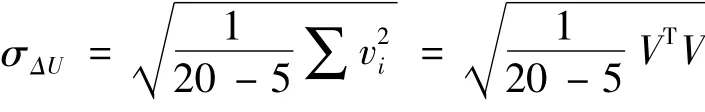
对于待辨识参数矩阵K,得到各参数的标准差估计值为
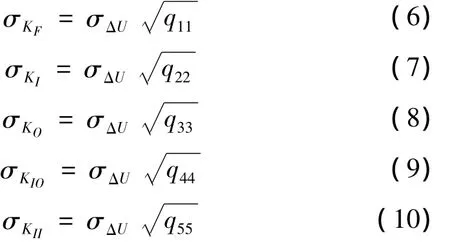
由公式(6)~(10)可知,未知参数的测量标准差均与矩阵Q对角线元素(q11,q22,q33,q44,q55)的平方根成正比。分别由表1和表2中的相关角度和相应的加速度计电压输出值产生的σΔU相差非常小(σΔU1=1.4031×10-6V,σΔU2=1.2771×10-6V),可以近似相等。假设两种方法的单位权标准差相等,通过计算表1、表2中的角度值产生的矩阵Q的对角线元素的大小,就可以比较等比力法和等角位置法对加速度计误差模型系数的影响情况,如表3所示。
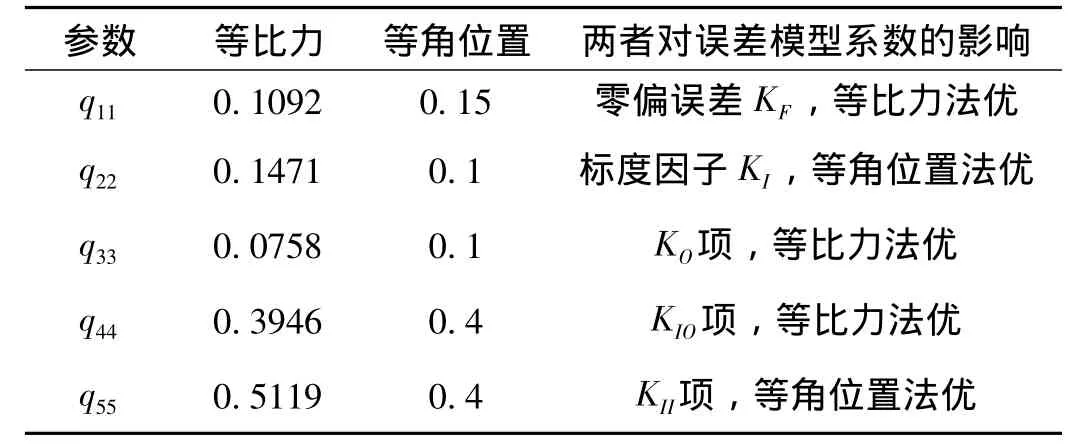
表3 等比力法与等角位置法对加速度计误差模型系数标定的影响
计算得到的等比力法与等角位置法测试加速度计的误差模型系数及其标准差,如表4所示。实际结果基本上与表3所分析的相符。通过两者对加速度计误差模型系数的比较,可以更好的选择最优方法提高加速度计主要参数KI,KF的标定精度,为加速度计后续离心机实验打下良好基础。

表4 数据处理结果
5 结论
本文就加速度计在重力场下的1g翻滚试验的两种方法——等比力法和等角位置法,分析了相应的加速度计误差模型系数的标定不确定度。通过实验数据对两种方法进行了误差分析,发现等比力法和等角位置法各有优缺点,具体表现为零偏误差KF项等比力法优,标度因子KI项等角位置法优,KO和KIO项等比力法优,KII项等角位置法优。因此,进行加速度计的重力场下静态翻滚试验时,选择等比力法标定零偏误差,等角位置法标定标度因子,更有利于提高加速度计的误差标定精度。
[1]Akia U,Mike O,Kohij S,et al.Calibration of three-aixs accelerometers using a three-dimensional vibration generator and three laser interferometers[J].Sensors and Actuators,A:Physical,2004,114(1):93-101.
[2]Hung Chao-Yu,Lee Sou-Chen.A calibration method for six-accelerometer INS[J].International Journal of Control,Automation and Systems,2006,4(5):615-623.
[3]IEEE Recommended Practice for Precision Centrifuge Testing of Liner Accelerometers[S].IEEE Std 836-2001.
[4]张红良,武元新,练军想,等.基于转台误差分析的高精度惯测组合标定编排改进[J].中国惯性技术学报,2010,18(1):129-134.
[5]任顺清,冯士伟,马向斌.加速度计的全组合标定方法[J].中国惯性技术学报,2007,15(6):760-764.
[6]董春梅,陈希军,刘庆博,等.正交双加速度计两种安装位置在重力场中的标定方法[J].中国惯性技术学报,2014,22(5):693-700.
[7]王大千,张英敏.加速度计1g重力场翻滚测试与误差分析[J].机械与电子,2009(1):34-36,60.
[8]邢海峰.精密离心机误差对加速度计标定误差的影响研究[D].哈尔滨:哈尔滨工业大学硕士学位论文,2009,6:54.
[9]苏宝库,蒋效雄,刘雨.加速度计几种模型辨识方法的比较研究[J].传感器与微系统,2011,30(3):40-42,45.

