宁波软土工程地质特性及本构模型研究

■吴伟良 ■浙江大学建筑设计研究院有限公司，浙江 嘉兴 314001

1 宁波软土研究现状

关于宁波软土工程特性的研究相对较少，目前已有的研究成果一般也只是针对某方面特性而展开的［1］。宁波软土研究最早可追溯到二十世纪五十年代，由浙江大学、铁科院合作研究，解决了宁波市铁路路堤地基稳定问题，开辟了宁波软土研究的先河。1981 年曾国熙等人对宁波软土进行了以强度为主的研究，指导了杜湖水库高坝地基的建设。1992 年朱向荣等人结合宁波烁社机场及舟山机场建设的经验，对软土变形进行了研究。二十世纪九十年代，在宁波地区大规模建设发展的要求下，软土的相关研究慢慢变热。苏伯苓对宁波地区软土的流变规律及工程实例应用进行研究，并取得显著成果。为解决萧甬铁路宁波段工程问题，1997 年周全能等人详细研究了宁波软土工程地质特征，并指导铁路建设的顺利完成。进入二十一世纪，宁波软土工程特性的研究越来越少，这与当今经济发展节奏完全不符，很有必要对宁波软土工程特性展开深入的研究，为各类工程提供必要的软土地质工程资料。

2 宁波软土工程地质特征

2.1 工程概况

宁波软土地貌多为滨海相淤积平原，软土覆盖面积广阔，工程场地基本分布于软土层之上［2］。造成宁波城区建筑沉降变形的主要软土层有两层:第一层由全新世海相淤积泥质土组成，厚度较大，含水量大，多为流塑状态，压缩性高，厚度为2～20 米;第二层为上更新世海积层，厚度为28～45 米，压缩性较第一层低，呈软流塑状态。宁波软土具有海绵结构和大型的层理构造，由于含有较多有机质、粘粒多、结合水丰富、颗粒间粘结力弱，因此压缩性较大，透水性差。本文主要以上述两层软土为例，对宁波软土工程地质特征及本构模型进行研究。

2.2 工程地质特征

根据宁波软土层的物理力学指标，可分析得到宁波软土具有的工程地质特征有:

(1)含水量高。软土的天然含水量w 一般超过液限wL5% 到10%，土体饱和度较高，液性指数大于1，Sr 大于94%，以粘性土软硬度为标准进行划分，软土处于流塑状态，流变性明显。

(2)孔隙率高，压缩性高。这类软土受压力后沉降比较大，属于高压缩性软土，孔隙率大于1，压缩系数平均值为0.76MPa-1，压缩模量在2MPa 到3MPa 之间。

(3)渗透性较差。软土层的颗粒成分以细颗粒为主，矿物成分以亲水性及活动性较大的矿物为主，液限WL在30%到50%之间，扩散层的水膜厚度较大，渗透系数小。垂直方向的渗透系数约为2.12x10-7cm/s，水平方向渗透系数约为3.94x10-7cm/s。由上述分析可知，软土地基上的建筑物的沉降周期较长，常常可达数十年，而且后期沉降比将会逐渐增大，因此在实际工程施工过程中应充分考虑到软土的次固结沉降。

(4)抗剪强度较低。在宁波软土地基修筑土坝、深基坑工程及路堤等工程时需要对软土地基进行预处理或基坑支护。因为软土粘聚力在4～30KPa 之间，内摩擦较小，直接影响到地基的承载力和边坡的稳定性。

(5)宁波软土灵敏度较高，灵敏度平均为4，属于中等灵敏度软土。灵敏度越大，表示土结构对强度的影响越大。由于宁波软土的灵敏度大，土结构与强度的联系较为紧密。宁波软土结构受扰动后，强度常常降低75%左右，这对工程施工是很不利的，因此需尽量避免土体受到扰动。

3 本构模型研究

3.1 弹塑性损伤模型［3］

(1)软土损伤基本理论

宁波软土的结构性较强，其受力时粒间联接不断被破坏，这种微观机制的变化使得软土的土力学性质发生了变化。我们把软土从原状土向重塑土过渡，并伴随着粒间结构破坏及颗粒结构重新排布的这个过程叫做损伤。1988 年沈珠江最早运用软土损伤对土体本构关系进行研究，奠定了土体损伤力学模型的基础。

采用损伤力学研究土体结构时可用损伤来描述土体结构破坏的过程，找出其演化的规律，并建立起含有损伤变量的本构方程。这样能更详细地描述天然软土在受力后所表现出的应变性状。

(2)损伤变量的确定

损伤变量就是在损伤力学中所定义的一个可以描述土体损伤演变过程的变量。根据损伤变量函数可计算出损伤变量的值:

W=(qu-q)/(qu-q’u)=1-e-a(ε1-εf)

qu、q’u 为原状土和重塑土在无侧限压缩试验中的应力峰值强度;q为应力峰值;εf为应力峰值qu所对应的轴向应变，ε1为应力值q 所对应的任一轴向应变;a 为损伤演化参数。

(3)建立本构关系

本文主要从损伤力学基本理论、应变增量的计算及弹性损伤矩阵三个方面对本构关系的建立进行介绍。

根据沈珠江(1993)提出的土体损伤理论，土体在受到压力的作用时，其变形过程可以看成由原状土向损伤土演变的过程，其力学参数可由下式计算得出:

S=(1-ω)Si+ωSd

S 为天然土体的力学参数，Si为原状土的力学参数，Sd为损伤土的力学参数，ω 为损伤比。

由弹性矩阵可推算出:

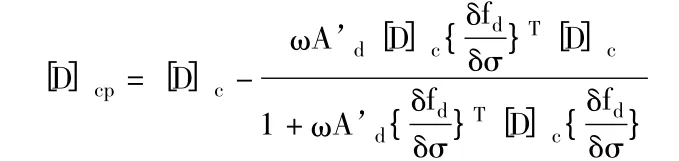
根据上式，可依次对ω、A’d、{δfd/δσ}T进行计算。

(4)模型参数的确定

弹塑性损伤模型的参数一共有9 个，分别为λ、k、M、e0、u、A0、ea、q0和P0，其中能确定的只有8 个，确定过程如下:

①确定修正剑桥模型参数(λ、k、M)

M=6sinΦ/(3-sinΦ)

Φ 为内摩擦角。

λ=Cc/ln10，k=Cs/ln10

Cc、Cs分别为压缩指数和回弹指数。

②其他参数的确定

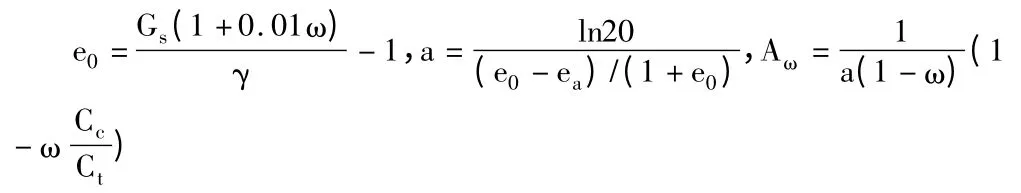
Gs为软土的相对密度;ω 含水量;γ 为软土的天然容重。

3.2 弹粘塑性模型

本文结合宁波软土蠕变实验结果，在Borja 模型的基础上，对弹粘塑性模型进行改进，用Mersi 模型代替singh-Mitchell 模型，建立一个适用于任何剪切应力水平范围的本构模型。Borja模型的软土蠕变包括体积蠕变和剪切蠕变两种，分别属于Taylor 次固结模型和singh 一Mitchell 模型，这两者都是通过引入滞后变形项来计算软土蠕变影响的［4］。

(1)体积蠕变模型t1

在相同固结压力的情况下，体积蠕变模型中软土的次固结系数一直保持不变。具体计算公式如下:

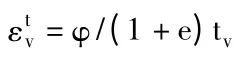
Φ=Ca/ln10，Ca为次压缩系数，tv为体积蠕变时间。

(2)剪切蠕变模型

剪切蠕变经验模型是建立在三轴流变实验的基础之上的，具体如下:

当时间一定时，该模型可简化成指数型应力-应力模型，适用于剪切应力在20%～80%之间的土体，而不能反映其他应力水平范围内的土体性状，尤其对应力水平低于20%的土体，效果极其不明显。

4 结语

宁波软土具有流变性明显及结构性较强两大特点，通过室内工作，笔者分析了宁波软土工程地质特征，对宁波软土含水量、孔隙度、渗透性、抗剪强度及灵敏度做出了详细解释。并且修正剑桥模型进行功能扩展，对宁波软土进行本构模型研究，介绍了弹塑性损伤模型与弹粘塑性模型两种本构模型。

［1］刘用海，朱向荣，吴健，等.宁波软土结构性成因及其对工程特性影响的研究［J］.工业建筑，2008，38(3):68-71.

［2］王文军，刘用海，朱向荣.宁波海相软土工程特性研究［J］.工程勘察，2008，(10):19-24.

［3］李金柱，朱向荣，刘用海.结构性软土弹塑性损伤模型及其应用［J］.浙江大学学报:工学版，2010，44(4):806-811.

［4］刘用海，李水明，俞伯华.宁波软土次固结特性试验研究［J］.土工基础，2009，23(3):77-79.