基于改进搜索特性的粒子群算法的水电站优化调度研究
唐海东,芮 钧,吴正义
(国网电力科学研究院/南京南瑞集团公司,江苏省南京市 210003)
基于改进搜索特性的粒子群算法的水电站优化调度研究
唐海东,芮 钧,吴正义
(国网电力科学研究院/南京南瑞集团公司,江苏省南京市 210003)
为了进一步提高水电站水库优化效果,减少弃水,提高水电站收益,本文以东风水电站为例,研究了粒子群算法的改进;改进了粒子自搜索、贪婪选择策略、优胜劣汰变异策略三项关键技术;并将改进的算法应用于水电站中长期优化调度。实例计算以基本粒子群算法、蜂群算法和提出的改进算法对同一电站进行优化。结果显示,改进的粒子群算法优于基本粒子群算法和蜂群算法,发电量和总收益都高于其他两种算法,弃水更少。结果证明改进的粒子群算法在求解具有复杂约束条件的非线性水库优化调度问题时,求解结果更优,收敛速度快的优点,为解决水电站中长期优化调度问题提供了一种新的有效方法。
改进粒子群算法;水库优化调度;自搜索
0 引言
水电站长期优化调度中,常用的调度模型求解算法主要是动态规划法、逐次优化法以及遗传算法等[1]。这些方法都存在着各自的缺点,如动态规划法存在维数灾、求解时间过长的缺点;逐次优化法属于贪婪算法,容易陷入局部最优解从而使计算速度大大降低;遗传算法则存在接近全局最优解时不易收敛,不易处理复杂约束条件等问题[1][2]。
粒子群算法是Kennedy等人提出的,用于解决优化问题的随机优化进化算法,由于原理简单,易于编程,收敛快,精度高等优点被广泛应用于各类工程问题。然而,水电站优化调度函数具有高维、多约束、非凸等特点,基本粒子群算法求解此类问题时极易收敛到局部最优值[3]。
因此,本文针对水电站优化调度问题的特点,对基本粒子群算法进行改进,并用于求解水电站中长期优化调度问题,解决基本粒子群算法求解该类问题时易陷入局部最优解的问题。
1 水电站中长期优化调度数学模型
水电站中长期优化调度主要是在满足电力系统出力要求以及下游航运、灌溉、生态等综合用水要求等的前提下,根据给定预报入库流量过程线,合理地安排水电站各个月份的发电流量,使得调度期内的总发电量最大或者总发电效益最大[4]。优化调度数学模型包括目标函数和约束条件两部分。使调度期内总发电效益最大,是水库优化调度最需要解决的问题之一。因此,本文以求取最大发电效益为目标。水电站调度期内的发电效益为调度期内各时段发电量与相应电价的乘积之和。
目标函数:

式中:E——调度期内的总发电量,kWh;
T——计算的调度时段数;
A——水电站出力系数;
Qgeni——第i时段内的平均发电流量,m3/s;
Hi——第i时段内的平均水头,m;
Mi——第i时段的时间长,h;
Pi——各时段的电价格。
约束条件:
(1)水量平衡约束,水库下一时段初蓄水量等于上一时段末蓄水量加来水量,再减去发电用水量和弃水量。
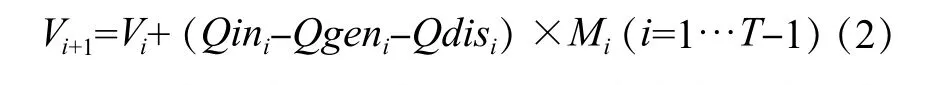
(2)水库蓄水量约束,各时段末水库蓄水量都不能超过它的上下限。

(3)发电流量约束,发电流量约束通常受机组自身过流能力限制,有时也受航运、灌溉、生态等因素限制。
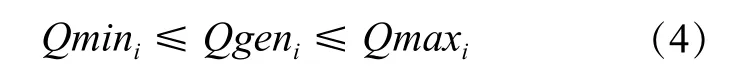
(4)电站出力约束,出力约束受电站机组的特性以及电力系统的要求限制。
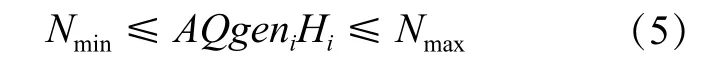
式中:Vi——第i时段初水库的蓄水量,m3;
Qgeni——第i时段的平均发电流量,m3/s;
Qdisi——第i时段的平均弃水流量,m3/s;
Ni——第i时段的平均出力,kW;
Vmini——第i时段允许的最小蓄水量,m3;
Vmaxi——第i时段允许的最大蓄水量,m3;
Qmini——第i时段下游综合用水要求的最小下泄流量,m3/s;
Qmaxi——第i时段下游防洪等要求的最大下泄流量,m3/s;
乌兰浩特地区日光温室性能优化及黄瓜促早栽培效益分析……………………… 张 鹏,崔世茂,宋 阳,张国华,叶丽红(124)
Nimin——第i时段电力系统要求的最小出力,kW;
Nimax——第i时段电站的允许最大出力,kW;
V0——水库初始蓄水量;
Vn——期末蓄水量。
2 改进的粒子群算法
2.1 改进粒子群算法分析
基本粒子群来源于计算机模拟鸟群觅食的社会行为,假设了鸟群随机降落某个空间并且拥有随机初速度,受自身记忆和全局最优粒子影响,来达到寻找最优值的目的。但实验仿真可验证其对于多峰函数或带有陡峭峡谷的函数可能收敛到局部最优,而非全局最优[5]。造成上述问题的原因是,粒子在飞行过程中缺乏对自身周围的局部探索能力,盲目的飞向迭代过程中的全局最优粒子,忽略了自身周围存在的更优位置,从而有可能飞跃过了最优位置。所以本文提出一种改进的粒子群算法,其粒子具有局部自行探索能力,飞行速度根据迭代次数自动减速,同时保留了粒子的社会性,仍然具有合作和知识共享的特性。
2.2 改进PSO算法关键技术
设在一个D维空间中,有m个粒子组成一个群体,其中第i个粒子表示为D维的向量xi=(xi1,xi2,…,xid,…,xiD)。每个粒子的位置就是一组解,将其对应的目标函数作为该粒子的适应值。因此,只需要将xi代入目标函数,就可以算出其适应值,并根据值的大小来衡量解的优劣。
2.2.1 改进粒子自搜索
开始时,所有粒子均随机散落在空间D中。根据粒子间的信息共享机制,各个粒子先向全局最优位置的方向移动,然后再向自己的周围各个方向以较小步长探寻,以式(6)进行:

其中,tV为某粒子加上某一步长后的适应度,i表示粒子编号,j表示方向编号,fitness为目标函数。
当粒子探寻到有效方向后,按式(7)计算移动速度。
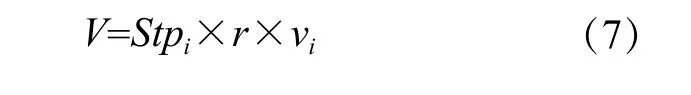
其中,v为第i粒子当前方向的移动速度,Stpi为第i粒子的步长因子,r为0到1间的随机数,方向向量vj=(0,0,…,cj,…,0)(cj=1)。然后按式(8)得到新的粒子位置。

2.2.2 粒子贪婪选择策略
2.2.3 粒子变异策略
当有两个粒子在空间上的距离distance<时,变异较差的粒子,即重新随机到D维空间中;当某粒子在设定的最小步长下,无法的再移动时,记录该粒子及适应值,然后变异该粒子。以此方法,增加粒子群多样性。
3 算法步骤
改进粒子群算法应用于水电站调度,以整个调度期内的发电效益为目标函数。将水电站各月初水库蓄水量组成的矢量作为粒子位置。
求解步骤:
Step1:初始化水电站的相关数据。
Step2:初始化粒子群,在限定范围中随机粒子的初始位置,产生单位方向向量vj(j=1,2,…,n),各粒子初始步长Stpi=(xmax-xmin)/10。Stpi为第i个粒子的初始步长,xmax为调度期内水库蓄水量上限,xmin为调度期内水库蓄水量下限。
Step3:选取粒子,先向全局最优位置方向寻优,再按照式(6)寻找有效方向,粒子向有效方向移动。直到在该步长下没有有效方向。
Step5:判断是否达到迭代次数?若是,则执行Step6;若否,缩短该粒子的寻优步长Stpi=Stpi/Δ(Δ为步长缩短因子),跳到Step3。
Step6:比较各粒子的收益,选取收益最高的粒子为需要找的最优解。
流程图如图1所示:
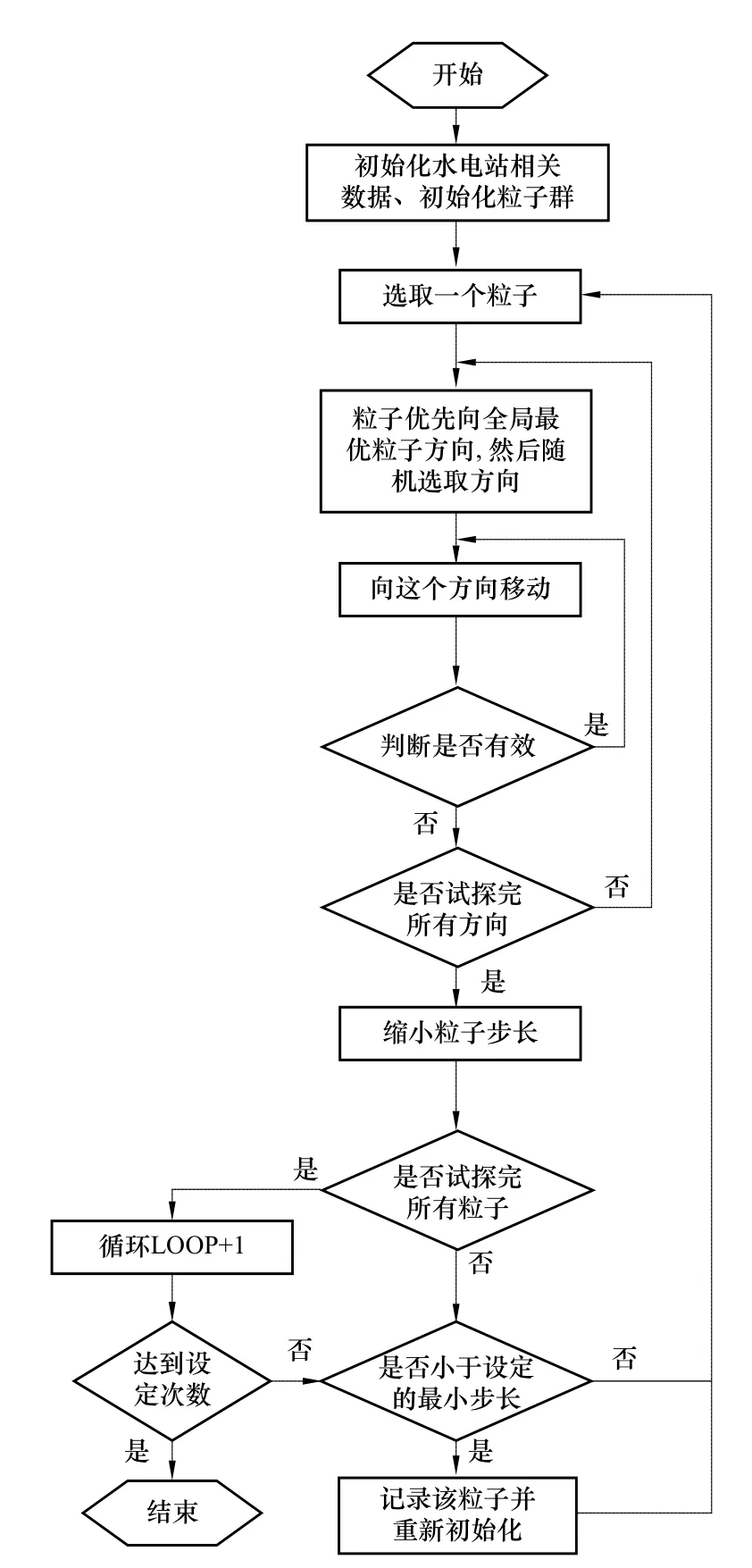
图1 算法流程图
4 计算实例
为了对本文提出的改进型粒子群算法求解水电站中长期优化调度问题进行可行性与有效性验证,以东风水电站为例进行中长期优化调度仿真计算。
东风水电站距省会贵阳88km,是乌江流域梯级开发的第二座水电站。现机组装机容量57万kW(3×19万kW)。水库正常蓄水位970m,相应库容10.25亿m3。死水位936m,相应库容5.35亿m3。调节库容4.9亿m3,属不完全年调节水库。坝址控制流域面积18161km2,占乌江流域面积的21%,多年平均流量343m3/s,平均年径流量108.9亿m3。充分、合理地运用其水库调节作用,可大幅度提高乌江干流的发电效益。因此对其开展优化调度研究意义十分重大。
给定水电站调度期内的初水位和末水位,调度期从6月初开始,到第二年5月底为止,为期1年,时段以月为单位。其中,汛期为6月~10月,电价为0.286元/kWh,11月至次年5月电价为0.356元/ kWh。起调水位为930m,期末水位为930m。来水采用某年的径流资料,其过程见图2。

图2 水电站水库入库径流过程线
为了验证上述改进算法的有效性,本文分别采用基本粒子群算法(PSO)、蜂群算法(BA)和改进的粒子群算法(改进PSO)编程计算求解。各算法所采用的参数分别为:基本粒子群算法,粒子数为500,w=1,c1,2=2。蜂群算法,侦察蜂、采蜜蜂都为100只。改进的粒子群算法,粒子数为60,Δ=10。经仿真计算,得到水电站调度期内的库容变化过程、出力过程、放水过程和各月的发电量、如图3和图4所示。三种计算方法得到的发电量和总效益结果对比如表1所示。

表1 三种算法计算结果对比
由表1可知,改进PSO算法计算的结果无论是总效益还是发电量,都优于其他两种算法。通过改进算法计算的结果要比另外两种算法分别多100万元、130万元。说明改进粒子群算法有效的优化了调度方案,有十分良好的寻优能力。

图3 库容变化过程
图3为水电站库容逐月变化过程,基本粒子群和改进粒子群算法大致趋势一样。7、8月份由于来水较多,三种算法在保证处理的情况下,蓄水方式不同。改进的粒子群算法在2~4月蓄水多于另两种算法。
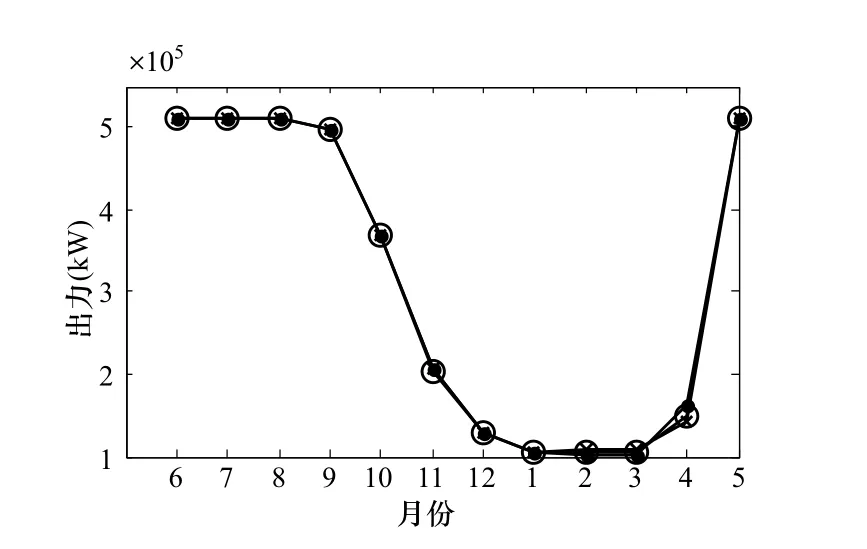
图4 出力对比
图4为水电站出力逐月变化过程,三种算法比较接近,但是改进的粒子群算法在2~4月出力比另两种算法多。

图5 弃水对比
图5为电站调度期内弃水过程对比。
综上可知,改进的粒子群算法搜索能力强,寻优能力更强,计算结果更优,适用于求解高维、多约束、非凸的水电站优化调度问题,可以进一步提高水能资源利用率,提高水电厂发电效益。
5 结束语
本文提出的改进粒子群算法在基本粒子群算法基础上增加了粒子自搜索、基于贪婪策略的移动、优胜劣汰的变异,是一种用于求解高维、多约束、非凸优化复杂问题的有效方法。该算法从全局范围内进行粒子自搜索,有效避免了粒子陷入局部最优;贪婪策略进一步提高了算法的收敛速度,保证了算法快速收敛;优胜劣汰的变异策略则实时地重新初始化不好的粒子和已经收敛到局部最优的粒子,确保了粒子的多样性和有效性。
本文将粒子群算法进行改进,并引入到水电站优化调度的应用。实验仿真计算结果表明,与基本粒子群算法及蜂群算法相比,改进的粒子群算法可以提高求解速度,增加调度期内的总收益,减少弃水。今后可进一步研究该改进粒子群算法求解梯级水电站群或混联水电站群水电联合优化调度问题。
[1] Luo P,Zhou J,Qin H,et al. Long-term Optimal Scheduling of Cascade Hydropower Stations Using Fuzzy Multi-objective Dynamic Programming Approach[C].//International Conference on Intelligent Computation Technology amp; Automation. IEEE,2011:174-176.
[2] 涂启玉,梅亚东. 遗传算法在水库(群)优化调度研究中的应用综述[J]. 水电自动化与大坝监测,2008,32(1):16-18.
[3] 段金长. 梯级水电站优化调度的改进粒子群算法[J]. 水电自动化与大坝监测,2009,33(5):8-11.
[4] 明亮,芮钧,徐松. 水电站优化调度人工蜂群新算法[J].水电自动化与大坝监测,2012,36(3).
[5] 黄少荣. 粒子群优化算法综述[J]. 计算机工程与设计,2009,30(8):1977-1980.
[6] 涂启玉,梅亚东. 遗传算法在水库(群)优化调度研究中的应用综述[J]. 水电自动化与大坝监测,2008,32(1):16-18.
[7] 段金长. 梯级水电站优化调度的改进粒子群算法[J]. 水电自动化与大坝监测,2009,33(5):8-11.
唐海东(1989—),男,硕士研究生,主要研究方向:水电站优化调度,人工智能。E-mail:tangtang5468@sina.com
芮 钧(1978—),男,博士,高级工程师,主要研究方向:水电厂及流域梯级的优化调度及自动发电控制。
吴正义(1968—),男,硕士,研究员级高工,主要研究方向:水电厂及流域梯级的优化调度及自动发电控制。
Application of based on Particle’s Search Features Improved Particle Swarm Optimization in the Optimal Operation of Hydropower Stations
TANG Haidong,RUI Jun,WU Zhengyi
(State Grid Electric Power Research Institute,Nanjing 210003,China)
In order to further improve the effect of optimal operation of hydropower stations,reduce water wastage,improve Hydropower Station revenue,taking Dongfeng Hydropower Station as an example,studies the improvement of particle swarm optimization algorithm,research three key technology of improved particle self-search,greedy selection strategy,the survival of the fittest mutation strategy and the improved algorithm is applied to the long term optimal operation of hydropower stations. An example is given by the basic particle swarm optimization algorithm,artificial bee colony algorithm and the proposed improved algorithm for the plant optimization.The results show that,the improved particle swarm algorithm is better than the basic particle swarm optimization algorithm and artificial bee colony algorithm,power generation and the total yield is higher than the other two algorithms,and less water. It proved that the improved particle swarm optimization algorithm gets the better results and has the advantages of fast convergence in solving the nonlinear reservoir optimal scheduling problem with complex constraints. It provides a new and effective method to solve the long-term optimal scheduling of hydropower station.
improved particle swarm optimization;optimal operation of hydropower stations;search feature

