局部阴影条件下光伏电池多峰值最大功率点控制策略

赵玉林，张冬梅，马文川，李京京

（东北农业大学电气与信息学院，哈尔滨 150030）

局部阴影条件下光伏电池多峰值最大功率点控制策略

赵玉林，张冬梅，马文川，李京京

（东北农业大学电气与信息学院，哈尔滨 150030）

局部阴影条件下，光伏阵列的P-V曲线会呈现多个局域峰值，影响最大功率点跟踪（MPPT），传统MPPT算法只能跟踪单个功率峰值，在局部阴影输出功率多峰值条件下，该算法不能完成有效跟踪。粒子群算法（PSO）有较强多极点寻优能力，但易陷入局部最优解。针对此问题，在粒子群算法中引入模拟退火算法的Metropolis选择机制，在简化所需设置参数同时帮助粒子群算法有效跳出局部最优解。在控制过程中，采用主程序加嵌套迭代双重判定条件，保证粒子稳定前提下，收敛在最大功率点（MPP）附近。通过MATLAB对比仿真验证，表明该算法在局部遮阴情况下能较精确、快速地跟踪到最大功率点，有效提高光伏电池输出效率。

多峰值MPPT；局部阴影；嵌套迭代；模拟退火粒子群算法（SA-PSO）

网络出版时间2015-4-30 14:29:00 [URL]http://www.cnki.net/kcms/detail/23.1391.S.20150430.1429.001.html

赵玉林,张冬梅,马文川,等.局部阴影条件下光伏电池多峰值最大功率点控制策略[J].东北农业大学学报,2015,46(5):89-94.

Zhao Yulin,Zhang Dongmei,Ma Wenchuan,et al.Multi-peak PV array control strategy under the conditon of partial shade [J].Journal of Northeast Agricultural University,2015,46(5):89-94.(in Chinese with English abstract)

光伏电池输出功率与光照强度相关，在正常光照条件下，光伏电池输出功率P-V曲线只存在1个峰值点，即最大功率点（MPP）。在局部阴影情况下，其输出功率P-V曲线呈现多峰值，扰乱最大功率点跟踪。在局部阴影情况下，如何对电池输出功率进行控制，使其保持最大功率输出是亟待解决问题。

目前国内外针对局部阴影条件下MPPT控制方法主要有：①针对传统单峰值MPPT算法改进，如斐波那契序列跟踪法[2]、改进电导增量法[3]、并联功率补偿法[4]、扰动观察改进法[5-6]、复合MPPT算法[7]等，虽在寻优速度上有较大提高，但精度不够，在峰值处仍有振荡，造成功率损失。②针对多极点寻优的智能MPPT算法，如粒子群算法及其改进算法[8-9]等。

粒子群算法具有搜索精度高、收敛性强等优点，广泛应用在各学科中，但粒子群算法易陷入局部最优解，将其直接应用在多峰值MPPT控制中，不能准确跟踪最大功率点。袁晓玲等提出自适应权重粒子群算法多峰值MPPT控制方法 ，但该种算法动态调整过程复杂、对参数依赖性强、控制难度大。孙博等提出粒子群改进算法，粒子分布位置范围不固定，不能严格约束粒子运动趋势，收敛速度慢[11]。朱艳伟等虽限定粒子运动范围，但其终止条件不能保证粒子收敛在最大功率点附近，误差较大[12]。

本文将模拟退火算法引入粒子群算法，即将模拟退火算法中核心思想Metropolis原则（一种动态概率的采样方式）为粒子优劣的判断条件，使粒子群算法摆脱局部最优解。改进算法具有对参数依赖性小、粒子的运动趋势协调、控制难度小等优点。在控制过程中，采用主程序加嵌套迭代的双重判定条件，有效解决粒子群算法易陷入局部最优解问题。最终通过仿真验证基于SA-PSO的控制策略能够有效跟踪最大功率点。[10]

1 基于模拟退火思想粒子群算法改进策略

1.1 融入模拟退火思想的粒子群算法

在粒子群算法中，每个粒子代表一个可能存在的解。首先要对粒子进行初始化，产生一组随机解，粒子可根据自身存在空间以往的飞行经验更新自身速度和位置[13]；在粒子群优化算法进行过程中[12]，应该设定出目标函数，计算其对应的适应值，并以此作为筛选合格粒子标准，选出局部最优粒子Pbest及全局最优粒子Gbest；根据事先设定的速度更新公式及位置更新公式计算下一代粒子位置和速度，如式（1）、（2），反复操作，最终求解出全局最优解[14]。

式中，c1是粒子自身学习因子、c2是粒子社会学习因子（c1和c2分别使粒子向Pbest和Gbest位置靠近）；r1、r2是0和1之间均匀分布随机数；k为迭代次数；Pid为局部极值的第d维分量，Gid为全局极值第d维分量。

模拟退火算法的寻优过程又称“暴力搜索”，作为模拟退火算法选择机制的Metropolis准则，是以动态概率为依据的采样方法[15-18]，动态概率P（t）随着迭代进程逐渐趋于零。在迭代开始阶段算法接受“恶化”粒子的概率较大，使得搜索过程具有突跳性，能够摆脱局部最优解；在后期接受“恶化”粒子的概率逐渐减小，有助于粒子趋近全局最优解。动态概率P（t）公式如式（3）所示：

式中，Ei、Ej为粒子前后状态；K为玻耳兹曼常数，取值1.38×10-23；R为当前迭代次数；Rmax为最大迭代次数。

本文以粒子群算法为主体算法，在是否接受后状态粒子判断过程中，引入模拟退火核心思想Metropolis准则，使粒子群算法在一定程度上接受“恶化”粒子，不强求后状态强于前状态，设置参数变量少，增加粒子群算法跳跃性。改进算法流程如图1所示。

1.2 SA-PSO算法性能验证

本文分别运用单峰值测试函数Rosenbrock函数如公式（4）、多峰值测试函数Griewank函数如公式（5），验证SA-PSO算法性能。

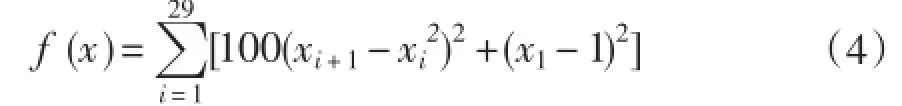
搜索范围（0,100）、全局最优值为f(0,0)=0。

搜索范围（0,1）、全局最优值为f(0,0)=0。

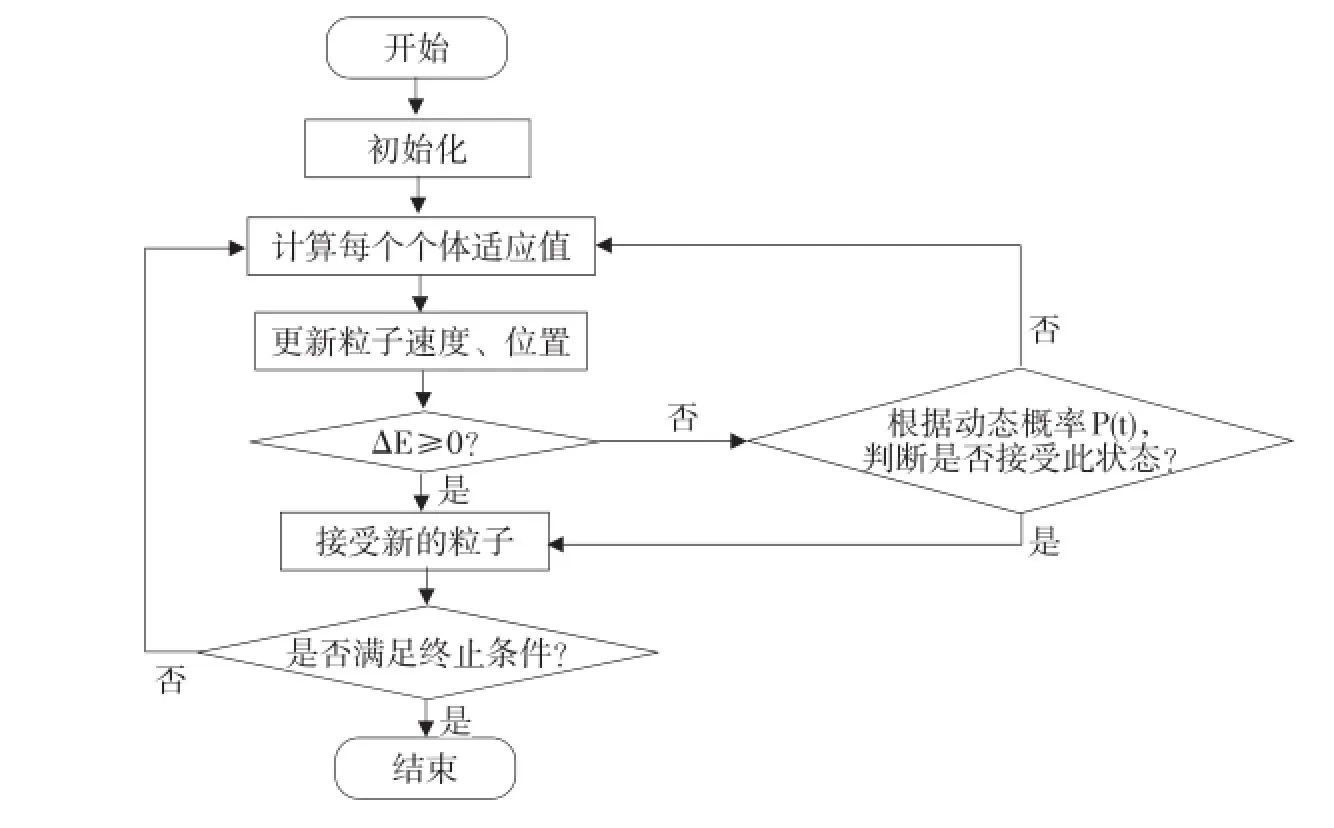
图1 SA-PSO算法流程Fig.1 Algorithm flowchart of SA-PSO

算法参数设置为种群规模10 N、维数10 D、学习因子c1=c2=2、最大迭代次数500次。运行结果曲线对比如图2、3所示。

由图2、3可知，在单峰值测试函数中这两种算法均能较为准确地找到全局最优值，在收敛速度方面，SA-PSO算法较快，后期收敛全局最优解过程中震荡较小；在多峰值测试函数中，PSO算法不能找到全局最优解，而SA-PSO算法收敛速度明显优于PSO算法，能准确找到全局最优解。

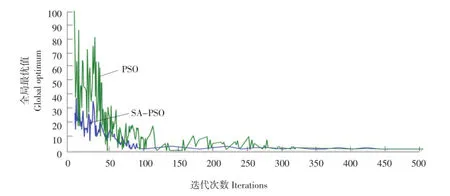
图2 Rosenbrock适应值对比曲线Fig.2 Contrast curve of Rosenbrock fitness

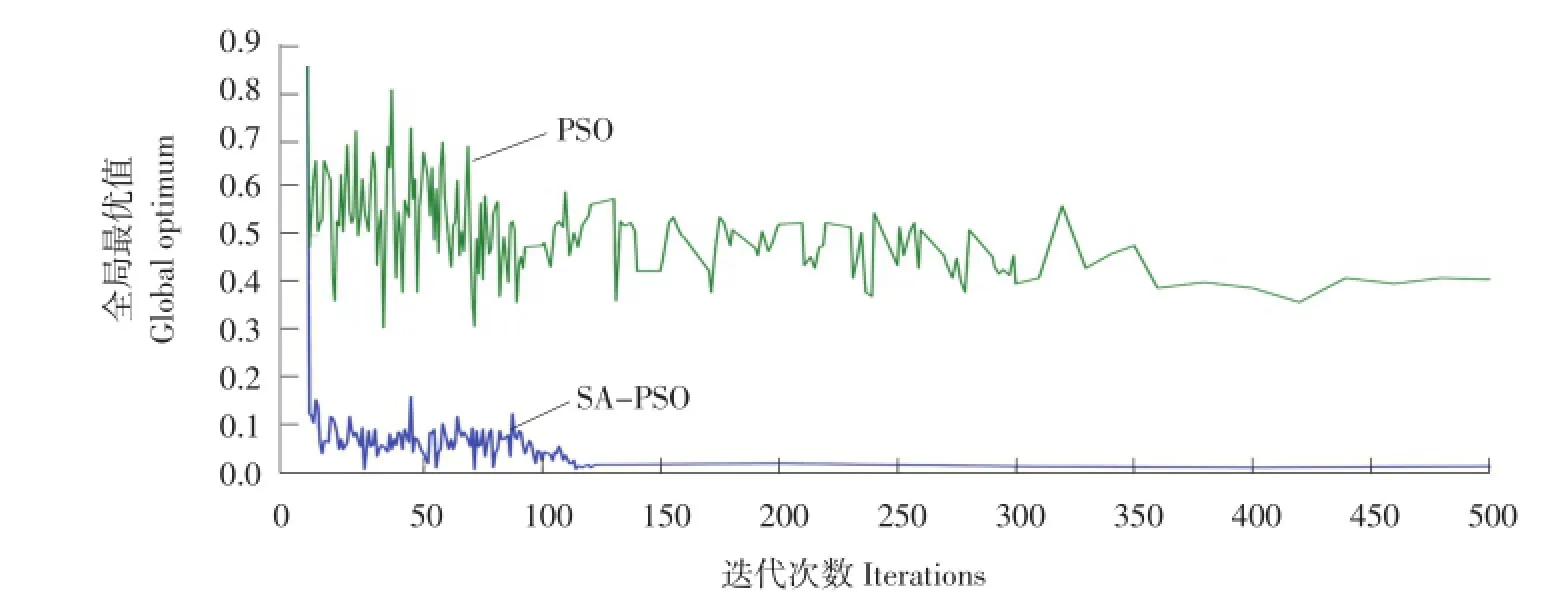
图3 Griewank适应值对比曲线Fig.3 Contrast curve of Griewank fitness

2 SA-PSO算法在MPPT多峰值的控制策略

在SA-PSO算法中，粒子不断改变位置，通过比较粒子所在位置适应值，更新粒子的位置，经过反复比较更新，最终找到最优解。SA-PSO算法在MPPT寻优中，粒子以电压作为可改变的位置变量，电压值作为适应值，根据适应值的判定条件，判断是否接受该状态。SA-PSO在MPPT多峰值寻优流程图如图4所示。

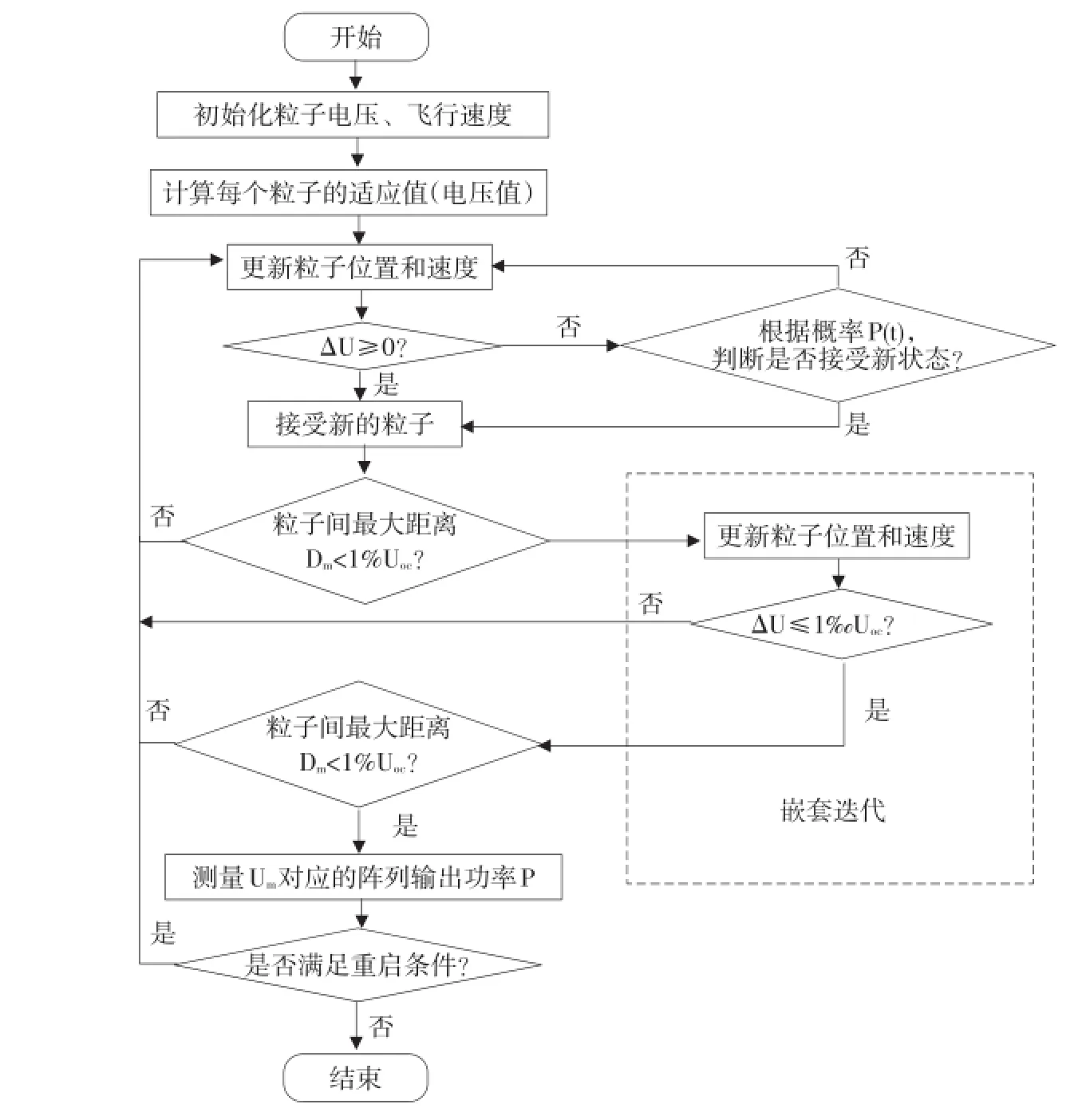
图4基于SA-PSO的MPPT控制流程Fig.4 MPPT control flowchart based on SA-PSO

初始化粒子位置（其所对应的电压值U）、速度；得到每个粒子的适应值（电压值U），更新粒子电压值和速度；判断后状态的适应值与前状态适应值差ΔU，当ΔU≥0时，即粒子往全局最优位置移动，接受此状态；否则，根据概率判断是否接受此状态，不接受新粒子返第四步，更新粒子的位置；当4个粒子间最大距离Dm≤1%Uoc时，进入嵌套迭代过程；嵌套迭代是判断每个粒子振荡幅度是否趋于稳定的依据，若粒子前后振荡幅度的电压差ΔU≤1‰Uoc，表明该粒子已稳定；稳定的粒子之间的最大距离Dm≤1%Uoc时，认为已找到全局最优值，通过其对应的电压值得到最大输出功率值Pmax；判断是否满足重启条件，若满足，重新更新粒子的位置和速度；若不满足，结束迭代。

3 基于SA-PSO的MPPT多峰值仿真

3.1 光伏电池多峰值仿真

多数情况下，光伏电池板各个部分接受的不同光照强度和灰尘等杂质影响电池输出效率。本文选取RAP60作为仿真电池型号，其短路电流Isc为3.55 A、开路电压Uoc为22.20 V、最大功率点额定电流Impp为3.36 A。在标准情况下（温度25℃、光照强度1 000 W·m-2）对RAP 60进行遮阴处理，分别以遮阴30%、50%、70%为例，根据额定参数，输出功率特性如图5所示。

由图5可知，在30%遮阴情况下第一个峰值Pmax31≈14.88 W、第二个峰值Pmax32≈43.20 W；在50%遮阴情况下Pmax51≈12.12 W、Pmax52≈32.30 W；在70%遮阴情况下Pmax71≈6.30 W、Pmax72≈19.30 W。由此可见，阴影会导致最大功率点出现多峰值，使跟踪最大功率点（MPP）的过程出现混乱。

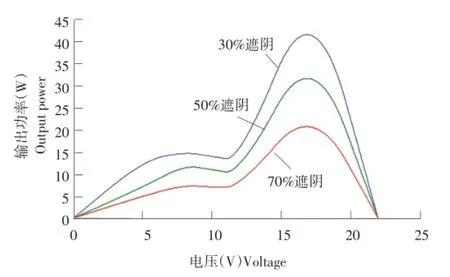
图5 RAP60在遮阴情况下的P-V特性曲线Fig.5 In the shade of the P-V feature curve of RAP60

3.2 MPPT仿真模型

本文光伏阵列采用RAP60，最大功率跟踪系统（MPPT）仿真框图如图6所示。

图6 最大功率跟踪系统仿真

Fig.6 Simulation diagram of MPPT system

BOOST电路的占空比如式（6）所示。

BOOST电路输入电压为光伏阵列的输出电压U，U0为蓄电池电压。MPPT控制器采用SA-PSO算法控制。MPPT输入端为光伏阵列的输出电流I及输出电压U，随光照减小，电流I也变小，此时输出功率降低。SA-PSO算法通过控制输出电压U，输出最大功率，按式（1）更新光伏阵列电压U，按式（6）计算占空比D，以驱动脉冲触发器PWM来控制MOSFET关断时间，使光伏电池运行在更新后的电压，并测出对应的输出功率。

3.3 仿真参数设定

①仿真参数设定：电路参数L=4 mH、C1=200 μF、C2=1 000 μF、蓄电池电压U0=50 V。SA-PSO算法参数学习因子c1=c2=2、惯性权重ω=2、主程序最大迭代次数为500、嵌套迭代最大迭代次数为10。

②粒子数目选取：在30%遮阴情况下，所选取电池型号为RAP60，其行列结构为36×1，根据文献[12]可知，m×n阵列电池可有n+1个峰值，一般情况下选取n+1个粒子。鉴于RAP60只有2个峰值，为更好观察SA-PSO算法优越性，本文选取4个粒子。

③初始化条件：粒子群位置分布在最大功率点（MPP）左侧，即搜索范围为0～17 V。

④终止条件：由于初始粒子位置分散，当粒子位置非常集中时，且每个粒子振荡幅度小于规定临界值时，可认为已达最大功率点（MPP）附近。本文设定，当粒子之间最大电压之差＜1%Uoc时，且每个粒子振荡电压差＜1‰Uoc时，当前所有粒子对应电压最大者定为Um，其功率为最大功率Pmax。

⑤重启条件：每隔2 min自动重启1次。

3.4 仿真结果对比分析

初始化后粒子电压及占空比如表1所示。

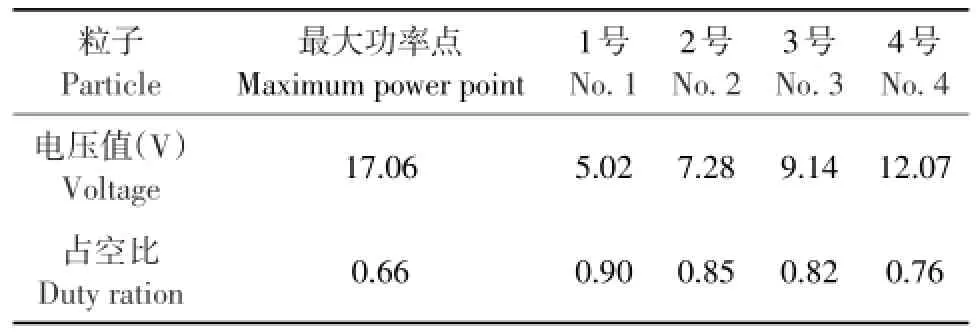
表1 粒子初始位置Table 1 Initial position of the particle

粒子通过不断改变自身位置，使其对应电压值变化，占空比D变化，通过占空比D来驱动PWM触发器，以调节MOSFET关断时间，使电池运行在更新后的电压值，实现根据算法迭代更新，输出电压值不断更新，功率随电压改变而改变，最终输出功率寻优曲线如图7所示。

由图7可知，基于PSO算法的功率输出曲线在约1.7 s趋于稳定，输出功率为14.53 W，粒子寻优结果最终陷入第一个功率峰值14.88 W附近，未跳出局部最优解限制。基于SA-PSO算法的功率输出曲线在约3.5 s趋于稳定，输出功率为43.09 W，粒子寻优结果最终停留在实际最大功率点附近，相对误差0.25%。在寻优时间上，基于SA-PSO算法的功率曲线到达稳定时间较长，因为SA-PSO算法的Metropolis选择准则及在控制流程中引入嵌套迭代判定过程，在一定程度上延迟寻优时间。在寻优准确度上，基于PSO算法的功率寻优控制过程未能摆脱局部最优解限制，使最大功率跟踪失效；基于SA-PSO算法功率寻优控制能准确、快速到达最大功率点附近，输出功率准确。

图7 输出功率寻优曲线Fig.7 Output power optimization curve

4结论

a.本文提出一种基于模拟退火思想粒子群改进算法（SA-PSO），即在PSO算法中引入模拟退火算法中Metropolis选择准则，避免粒子群算法（PSO）陷入局部最优解。通过测试函数Rosenbrock、Grie⁃wank验证改进算法具有快速跳出局部最优解、准确寻找全局最优解能力。

b.本文在MPPT控制过程中采用嵌套迭代，测试粒子稳定性，与SA-PSO算法选择机制构成双重判定条件，保证粒子在稳定前提下收敛在最大功率点（MPP）附近，有效避免SA-PSO算法选择机制偶然切合，影响最大功率输出。

c.通过仿真对比验证，SA-PSO改进方法能在多峰值MPPT寻优中摆脱局部最优点，准确找到最大功率点（MPP），有效提高光伏发电效率。

虽然该控制模式能较准确找到最大功率点，但尚需改进完善。由于在改进控制环节中进入双重判定条件，寻优时间较传统PSO算法长，需对前期粒子性能方面进行更好的训练。

[1] 吴红斌,陶晓峰,丁明.光伏并网发电系统的MPPT电压控制策略仿真[J].农业工程学报,2010,26(1):267-271.

[2]李晶,窦伟,徐正国,等.光伏发电系统中最大功率点跟踪算法的研究[J].太阳能学报,2007,28(3):268-273.

[3]董密,杨建,彭可,等.光伏系统的零均值电导增量最大功率点跟踪控制[J].中国电机工程学报,2010,30(21):48-53.

[4] 崔岩,白静晶.光伏阵列多峰最大功率点跟踪研究[J].电机与控制学报,2012,16(6):87-91.

[5]刘邦银,段善旭,刘飞,等.基于改进扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009(6):91-94.

[6]党克,杨维湘,严干贵,等.光伏发电系统MPPT改进方法研究[J].电网与清洁能源,2013,29(4):91-95.

[7] 高金辉,唐静.一种新型光伏系统最大功率跟踪算法的研究[J].电力系统保护与控制,2011,39(23):21-24.

[8] 王福林,吴昌友,杨辉.用遗传算法求解约束优化问题时初始种群产生方法的探讨[J].东北农业大学学报,2004,35(5):608-611.

[9] 徐梅,文士发,王福林,等.遗传算法求解约束优化问题时产生初始种群的改进方法[J].东北农业大学学报,2014,233(7): 104-107.

[10] 袁晓玲,陈宇.自适应权重粒子群算法在阴影光伏发电最大功率点跟踪(MPPT)中的应用[J].中国电力,2013(10):85-90.

[11] 孙博,梅军,郑建勇.局部阴影条件下最大功率点跟踪改进算法[J].电力自动化设备,2014,4(1):115-119.

[12] 朱艳伟,石新春,但扬清等.粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用[J].中国电机工程学报,2012,2(4):42-48.

[13] Kennedy J,Eberhart R.Particle swarm optimization[C].Proceed⁃ings of IEEE international conference on neural networks,1995: 1942-1948.

[14]纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009.

[15] Kirkpatrick S,Vecchi M P.Optimization by simmulated annealing [J].science,1983,220(4598):671-680.

[16] Van Laarhoven P J M,Aarts E H L.Simulated annealing[M]. Springer Netherlands:D.Reidel Publishing Co.,1987.

[17] Johnson A A,Flegal J M.A modified conditional Metropolis-Hast⁃ings sampler[J].Computational Statistics&Data Analysis,2014, 78:141-152.

[18] Vihola M.On the stability and ergodicity of adaptive scaling Me⁃tropolis algorithms[J].Stochastic Processes and their Applica⁃tions,2011,121(12):2839-2860.

Multi-peak PV array control strategy under the conditon of partial shade

ZHAO Yulin,ZHANG Dongmei,MA Wenchuan,LI Jingjing(School of Electricity and

Information,NortheastAgricultural University,Harbin 150030,China)

On the condition of partial shade,the PV curve of PV array will show multiple local peaks, impacting the maximum power point tracking(maximum power point tracking,MPPT).Traditional MPPT algorithm can only track a single power peak output power of more than partial shade in peak condition next, the algorithm could not be completed effectively tracked.Particle swarm optimization(particle swarm optimization,PSO)had good multi-pole optimization capability,but it was easy to fall into local optimal solution for this problem,the introduction of Metropolis simulated annealing algorithm selection mechanism in particle swarm algorithm,at the same time simplifying the help needed to set the parameters of particle swarm algorithm effectively out of local optima.In the control process,the proposed main plus nested iteration of this new thinking ahead to avoid particle convergence,to ensure the convergence of particles can be near to the maximum power point(MPP).Ultimately through MATLAB simulation of the algorithm showed that the algorithm in the case of partial shading could be more accurately and quickly track the maximum power point,effectively improve the output efficiency of photovoltaic cells.

multi-peak MPPT;partial shade;nested iteration;simulated annealing particle swarm optimization(SA-PSO)

TM615

A

1005-9369（2015）05-0089-06

2014-09-09

东北农业大学电信学院攻关计划（IBHZ11228）

赵玉林（1956-），男，教授，硕士生导师，研究方向为电力系统自动化技术，E-mail:zyl5631@163.com