提高单板钴源剂量率MCNP计算效率的模拟研究
李 磊 李晓燕 黄 玮 蒋树斌 伍晓利 杨桂霞
(中国工程物理研究院 核物理与化学研究所 绵阳 621900)
提高单板钴源剂量率MCNP计算效率的模拟研究
李 磊 李晓燕 黄 玮 蒋树斌 伍晓利 杨桂霞
(中国工程物理研究院 核物理与化学研究所 绵阳 621900)
蒙特卡罗方法是目前准确的吸收剂量率计算方法,但其较长的模拟耗时阻碍了它在工业钴源辐射加工和辐照实验中的应用。模拟耗时、模拟精度以及模拟值与实测值的相对偏差是表征蒙特卡罗计算效率的重要指标。针对8.4PBq的单板钴源辐照装置,讨论了并行线程数、记数方法、记数栅元尺寸、γ致电子的处理方式和截断能5种参数对蒙特卡罗程序MCNP吸收剂量率计算效率的影响。利用实验测量结合模拟试算的方法,给出了在保证一定精度和相对偏差前提下,使得模拟耗时最少的参数组合,提高了MCNP计算效率。结果如下:超线程模式下的并行计算、*F6记数方法、栅元边长为1cm、γ输运模式、γ截断能为100keV。
单板钴源辐照装置,吸收剂量率,MCNP,计算效率
单板钴源辐照装置γ辐射场具有均匀区域大(几十至几百cm)、剂量率高(几百至上千Gy.min−1)的特点,除辐射加工外,还适合于大尺寸部组件辐照考核以及高剂量率条件下组件/材料辐射效应研究。了解辐射场吸收剂量率分布情况是准确剂量率辐照预先定位及累积吸收剂量掌控的重要前提。蒙特卡罗方法是目前准确的吸收剂量计算方法,但存在收敛速度慢、计算时间长的缺点,阻碍了其在单板钴源辐照装置吸收剂量率计算中的应用。MCNP (Monte Carlo N Particle Transport Code)是功能强大的蒙特卡罗程序,可模拟电子、γ和中子在复杂几何中的输运过程,其模拟准度已经通过诸多实验的验证,在辐射防护与辐照加工等领域发挥了重要的作用。文献[1–3]利用MCNP计算了单板钴源辐射场在不同介质中的吸收剂量率,其中文献[1]报道的模拟耗时为40 h。
模拟耗时表征模拟速度快慢,模拟精度表征模拟值的统计误差,是蒙特卡罗方法固有的偏差。模拟耗时、模拟精度以及模拟值与实测值的相对偏差(简称相对偏差)可用于描述模拟计算效率。除问题的固有复杂程度外,MCNP模拟计算效率还与模拟参数相关,包括记数方法、记数栅元尺寸、截断能以及γ致电子的处理方式等。(1) *F6和*F8是MCNP 中计算吸收剂量的主要记数方法[4],*F8通过直接记录栅元中γ和电子损失的能量给出吸收剂量,是MCNP中最接近吸收剂量定义的记数方法;*F6通过估算栅元的γ体通量给出比释动能,其它一些记数方法,比如面通量(F2)、体通量(F4、FMESH)等也可以通过注量-剂量转换法来计算比释动能,但是其本质都和*F6一样,即通过γ注量与响应函数的卷积计算比释动能,在带电粒子平衡(Charged Particle Equilibrium)条件下,比释动能与吸收剂量比较接近;一般而言,*F8的耗时较长、相对偏差小,而在模拟精度相同时,*F6耗时较少;(2) 较大尺寸的记数栅元可以增大有效事件的概率,以减小模拟精度和栅元空间分辨率为代价,来提高精度、减小模拟耗时;(3) 电子在介质中的频繁碰撞会耗费大量的模拟时间,取较低的截断能,可以保证模拟精度和准度,但模拟耗时会大为增加。此外,MCNP5支持并行计算,可在保证模拟精度和相对偏差不变的条件下,大幅减小模拟耗时。
关于MCNP 模拟参数的选取没有统一的标准,大多根据蒙特卡罗理论、实际需求和经验粗略选取参数,通过试算配合有限的实测值来调整参数,直至模拟值与实测值相符合后确定参数。邱有恒等[4]研究了栅元尺寸、δ电子、能量子步数和电子截断能对计算效率的影响,建议使用*F6与*F8联合记数,并提出了次级电子截断能的自适应方法来提高*F8的记数效率。林辉等[5]研究了头部放疗实例中MCNP截断能、记数方法和γ致次级电子产生参数对*F8记数效率和速度的影响。目前国内尚无关于提高钴源辐照装置吸收剂量率MCNP计算效率方面的报道。
本工作以某辐照站装源量为8.4PBq的单板钴源辐照装置为对象,讨论了MCNP中并行线程数、记数方法、记数栅元尺寸、截断能和γ致次级电子处理方式对空场吸收剂量率模拟计算效率(模拟耗时、模拟精度以及模拟值与实测值的相对偏差)的影响,从而寻求在一定模拟精度和平均相对偏差前提下,使得模拟耗时最少的参数组合,为利用MCNP计算大、中型钴源辐照装置辐射场吸收剂量率提供参考数据。
1 辐照装置与模拟过程
辐照装置的设计装源量为18.5PBq,最大可容纳180根源棒。模拟时的装源量为8.4PBq,根据剂量场均匀性的优化设计,50根源棒[6](活度分布见表1)分三层垂直排布在源架上。图1给出了MCNP中几何模型的示意图,表2给出了主要结构及其参数。模拟中的初始γ:(1) 位置,在单根源棒中均匀分布,不同源棒中的数量与活度成正比;(2) 能量,1.17MeV或1.33MeV;(3) 方向,4π各向同性。以矩形空气块作为记数栅元,分别采用*F8和*F6记数。整个模拟计算是在服务器(硬件:CPU,Intel Xeon X5675,3.07GHz;内存:32GB;Windows Server 2003操作系统)上进行的,MCNP版本为MCNP5,并行计算程序为MPI version1.2.5。
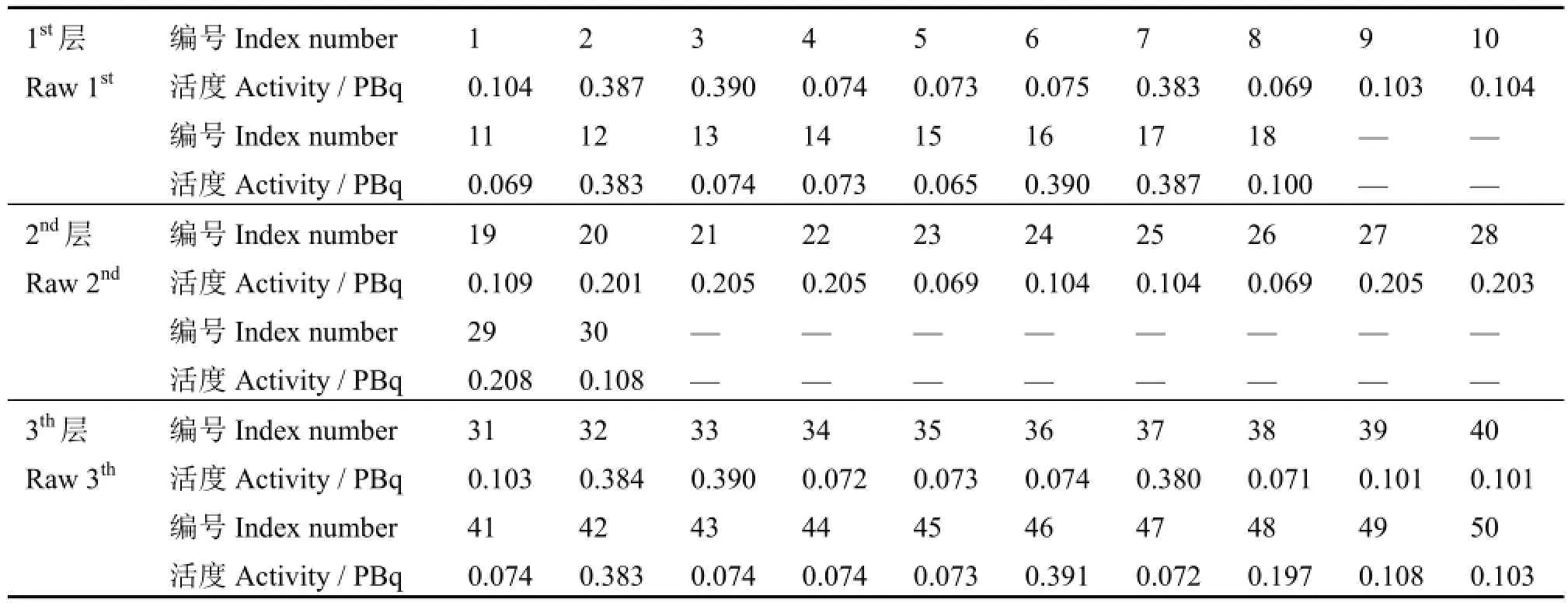
表1 源棒活度分布Table 1 Activity distribution of source bars.
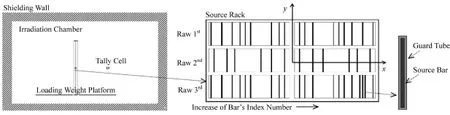
图1 MCNP中几何模型示意Fig.1 Scheme of geometry in MCNP.

表2 模拟中的主要结构及参数Table 2 Major structures and their parameters used in simulation.
利用重铬酸银化学剂量计测量空间点的吸收剂量率[7],为减小测量误差对单个空间点连续进行3次测量后取平均值。本文的吸收剂量率均为空气介质吸收剂量率。实测值为水吸收剂量率,按文献[8]方法换算为空气吸收剂量率(模拟计算结果表明换算方法的误差约为1.9%)。在距离源架30–115cm的常用辐照空间中,模拟和实测了10个空间点的吸收剂量率。
模拟精度σstat定义为多个空间点平均吸收剂量率X的统计误差,计算式分别为:
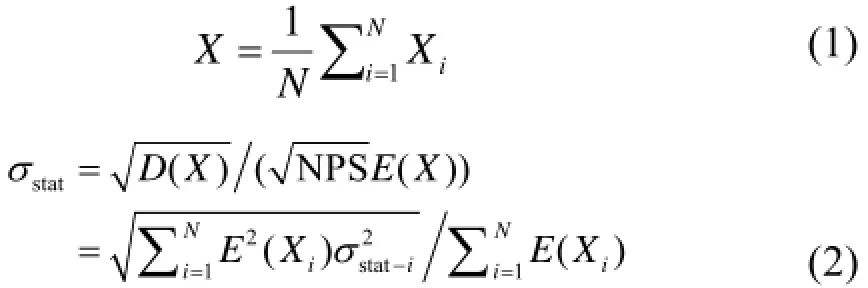
式中,i为空间点的序号;Xi为i点处的吸收剂量率;D(X)为样本方差;NPS为抽样数;E(X)为平均吸收剂量率X的期望;E(Xi)为i点处吸收剂量率的期望;σstat–i为i点处吸收剂量率计算值的统计误差;N为空间点的总数,为10。
平均相对偏差σm定义为多个空间点吸收剂量率实测值与模拟值相对偏差的均值,其计算式为:
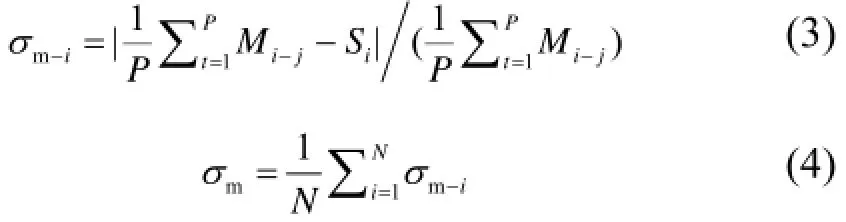
式中,j为测量序号;P为测量次数,为3;Mi−j为i点处吸收剂量率的第j次测量值;Si为i点处吸收剂量率的模拟值,即式(2)中的E(Xi);σm−i为i点处模拟值相对实测值的偏差。
讨论步骤为:(1) 栅元尺寸对*F8和*F6计算效率的影响;(2) 并行线程数对*F6模拟耗时的影响;(3) 电子截断能、γ致次级电子处理方式对*F6计算效率的影响;(4) 光子截断能对*F6计算效率的影响。前一步确定的参数,用于后续步骤中的模拟。模拟中采取接续运行的方式,直到吸收剂量率峰值的统计误差小于0.5%、σstat小于1%。平均相对偏差σm的限值为2%,模拟的粒子数NPS在2×108–2×109。
2 结果与讨论
2.1 栅元尺寸对计算效率的影响
本工作以矩形空气块作为记数栅元,用边长表征栅元的尺寸。表3给出了利用单核计算所得边长L对计算耗时t、模拟精度σstat和平均相对偏差σm的影响。图2给出了吸收剂量率模拟值和计算值的对比。由表3和图2可知:(1) 对于*F8记数方法,由于空气密度较低,对γ和电子的阻止能力弱,使得有效事件的概率低,边长5 cm的栅元、2×109个粒子数可使σstat=0.39%满足要求,但此时σm=16.43%仍不满足要求,这是因为模拟值是整个栅元介质吸收剂量率的平均值,若栅元过大,模拟值将不能用于准确描述栅元中任意点的吸收剂量率,因此*F8记数方法不能同时获得满意的模拟精度和平均相对偏差,不适用于本文所讨论的问题;(2) 对*F6记数方法,近似为常数,该结论可用于模拟参数的粗选;(3) 对*F6记数方法,计算速度与*F8相近(约3000photon.s−1),但收敛速度比*F8快得多,采用边长为0.5–5cm的栅元均可获得模拟精度和平均相对偏差较好的模拟结果,0.5cm情况所需的模拟耗时约为1cm情况的5倍;(4) 记数方法一定程度决定了模拟计算的可行性,合适的栅元尺寸可在保证模拟精度和平均相对偏差前提下大幅减小模拟耗时,因此记数方法对计算效率的影响较大。
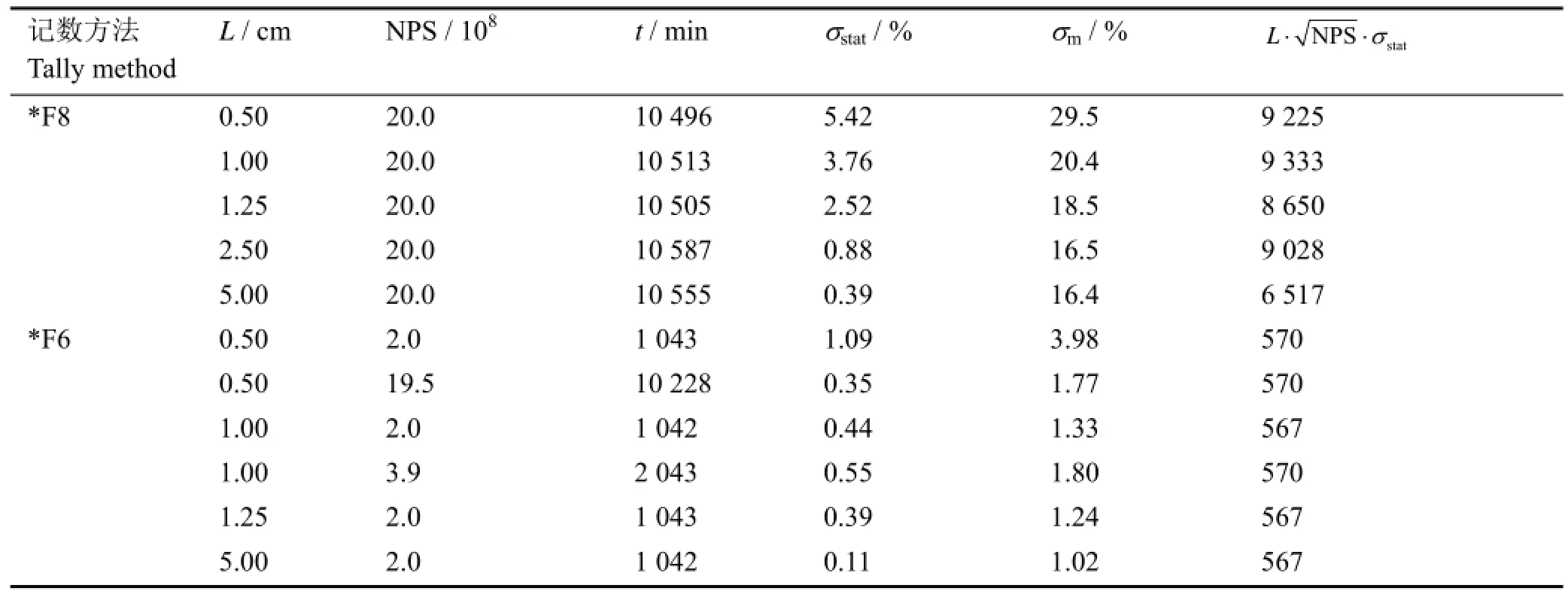
表3 不同栅元边长下的MCNP计算效率Table 3 MCNP computational efficiency under different cell size.
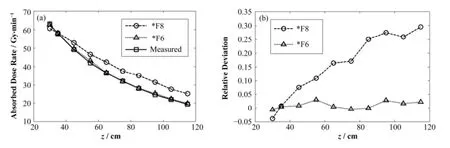
图2 吸收剂量率模拟值和计算值的对比 (a) 吸收剂量率值,(b) 模拟值相对测量值的偏差*F8和*F6记数栅元的边长分别为5cm和1cm,(x,y)=(0,0)Fig.2 Contrast of simulated and measured absorbed dose rate, where (x,y)=(0,0). The size of *F8 and *F6 were 5 cm and 1 cm, respectively. (a) Value, (b) Relative deviation, measurements as benchmark
文献[1−2]中栅元边长的最小值均为1cm,对于单板钴源辐照装置1cm的空间分辨率足以较好地描述剂量率场的分布。综上,后续讨论中选用*F6记数方法、栅元边长1cm作为模拟参数,模拟的粒子数均为3.9×108。
2.2 并行线程数对模拟耗时的影响
加速比S是衡量并行计算性能的重要指标,其计算公式[9]为:

式中,n为参与并行计算的线程个数;t1为单线程计算所用时间,min;tn为n个线程计算所用时间,min。
一个程序通常含有并行部分以及无法并行化的串行部分,因此使用n个线程并行计算能达到的加速比只能≤n。英特尔处理器的超线程技术通过采用特殊硬件指令把一个物理线程模拟两个逻辑线程,逻辑线程也可以并行工作。由于逻辑线程共享物理线程的资源,超线程模式下的加速比通常不能达到非超线程模式的两倍。默认情况下计算机操作系统开启超线程模拟,用户可通过设置BIOS进入非超线程模式。
MCNP程序的并行计算性能与问题的类型、复杂程度及参数设置等因素有关[10]。表4给出了本文所述问题并行线程数n与加速比S的关系。由表4可知,(1) n1/n2=2时,S1/S2为1.20–1.28,即超线程模式下的并行计算加速比约为非超线程模式的1.20–1.28倍;(2) 超线程模式下23个线程并行计算可获得最大加速比13.1;(3) 若继续增加并行线程数,可获得加速比的持续增大,其对计算效率的影响大于栅元尺寸。后续讨论中,均采用超线程模式下23个线程并行计算。
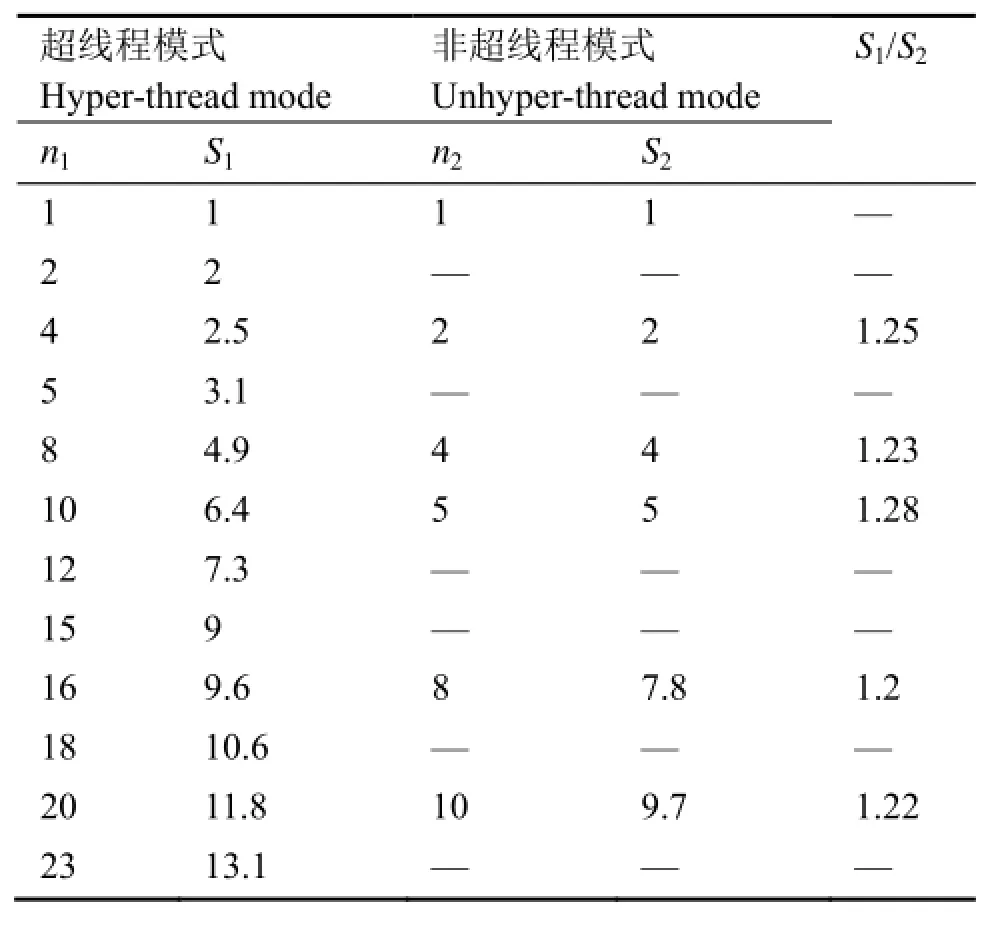
表4 并行计算线程数目与加速比的关系Table 4 Relationship between parallel threads and speed-up ratio.
2.3 电子截断能、γ致电子的处理方式对计算效率的影响
*F6统计栅元中的γ,除γ与介质的碰撞过程外,γ致电子与介质碰撞过程也会产生次级γ,这些γ会影响*F6的统计结果。MCNP 中γ致电子有三种处理方式[11]:(1) γ-电子耦合输运模式(即MODE P E),电子正常输运;(2) 电子致次级γ近似处理模式(即MODE P),此时电子不输运,而采用厚靶韧致辐射模型(Thick Target Bremsstrahlung)模式做近似处理;(3) γ输运模式(即PHYS卡IDES=1),电子也不输运,产生后仅在“原地”沉积能量,无次级γ的产生,该模式对*F6统计结果无贡献。在方式(1)中,采用较大的电子截断能Ee-cut,可获得模拟速度的提升,但会影响模拟值的平均相对偏差。
表5给出了不同电子截断能和γ致电子的处理方式对计算效率的影响:情况(1) γ-电子耦合输运模式,Ee-cut为1keV−1MeV,1keV是MCNP默认值;情况(2)电子致次级γ近似处理模式;情况(3) γ输运模式。根据文献[5],若两条峰值误差小于2%的曲线相比,其90%的剂量点的相对误差小于3%,就可以认为两条曲线近似相等。图3以γ-电子耦合输运模式Ee-cut=1keV为基准,对情况(1)、(2)和(3)的计算值进行了对比。由表5和图3可知,(1) 三种情况下的模拟精度σstat一致,平均相对偏差σm的变化不大,说明电子截断能、γ致电子的处理方式对模拟结果的影响可忽略,这是由于空气密度较低,γ与之发生作用的概率小,使得γ致电子的产额低,其对*F6记数的贡献也就小,因此改变γ致电子的处理方式不足以引起*F6统计结果明显改变,相较而言,栅元尺寸对计算效率的影响更大;(2) 由于没有γ致电子及其次级γ的输运,情况(3)模拟耗时最少,与默认值相比耗时减小约4倍。
综上,后续选用PHYS卡IDES=1(即γ输运模式)作为模拟参数。
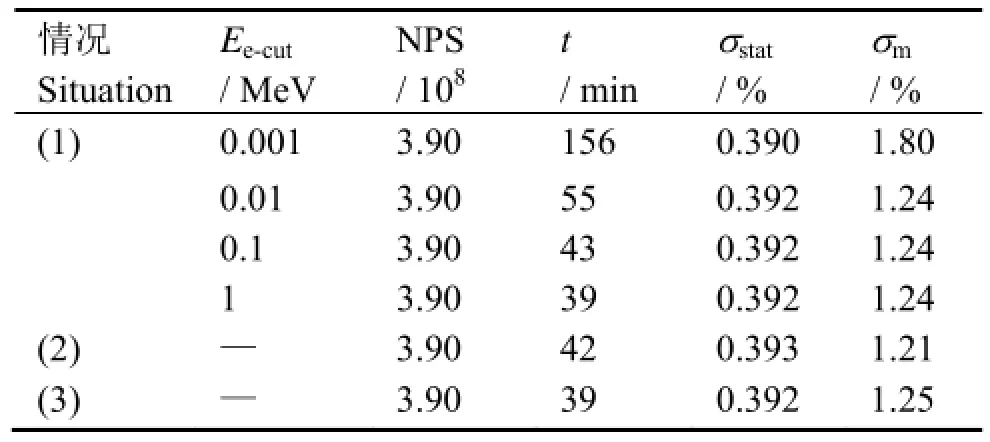
表5 不同电子截断能和γ致次级电子处理方式下计算效率Table 5 Computational efficiency under different electron cut-off energy and methods dealing with γ-induced electrons.
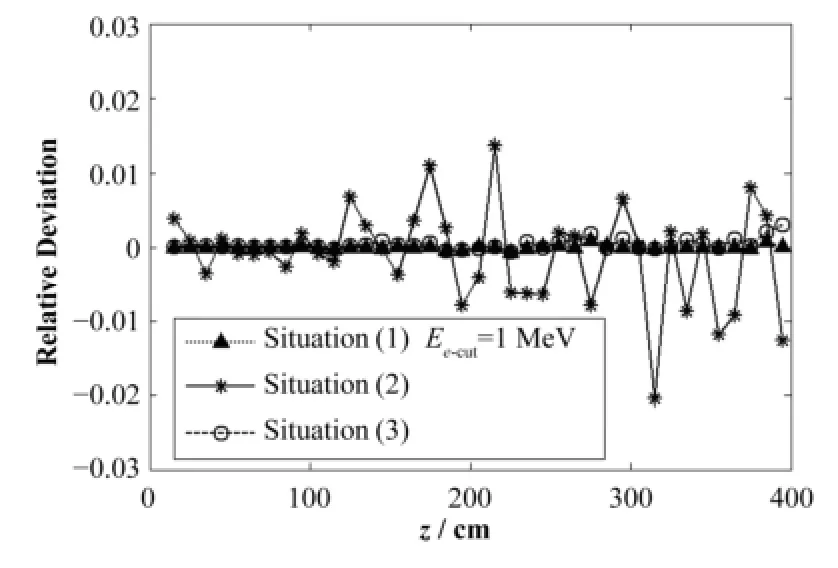
图3 不同γ致电子处理方式下的相对偏差Fig.3 Relative deviation under different methods dealing with γ-induced electrons.
2.4 γ截断能对计算效率的影响
表6给出了不同γ截断能Eγ-cut对t、σstat和σm的影响。由表6可知,(1) 直到Eγ-cut=300keV,σstat和σm仍然满足要求;(2) Eγ-cut=1keV时模拟值较实测值偏大,随着γ截断能增大,*F6计数率减小,σm出现先减小后增大的现象;(3) 光子截断能的提高,对模拟速度的影响并不显著,相较γ致电子的处理方式和电子截断能而言,γ截断能对计算效率的影响更小。
图4以Eγ-cut=1keV (MCNP默认值)为基准,讨论了不同γ截断能对计算效率的影响。由图4可知,(1) 随着γ截断能的增大,*F6模拟值逐渐减小,这是由于能量低于Eγ-cut的γ被“截断”后对*F6没有贡献,增大Eγ-cut使得进入记数栅元γ的数量减小;(2) Eγ-cut相同时,随着距离增大相对偏差逐渐变大,这是由于墙面散射γ的影响,距离越大越靠近墙面,散射γ比重越大;(3) 直到Eγ-cut=0.5MeV,90%剂量点的相对偏差都小于3%。
出于保守考虑,建议采用Eγ-cut=0.1MeV,与Eγ-cut默认值相比,模拟耗时减小约1.1倍。
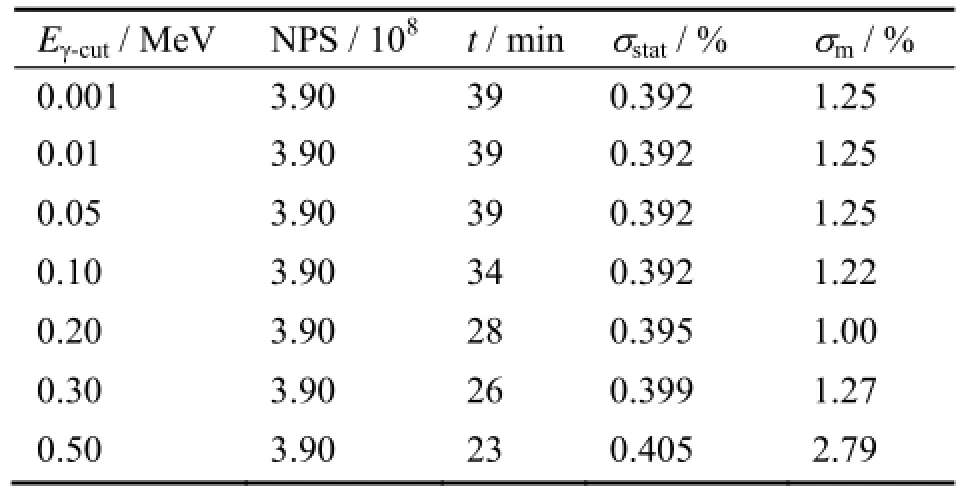
表6 不同γ截断能下的计算效率Table 6 Computational efficiency under different effect of γ cut-off energy.
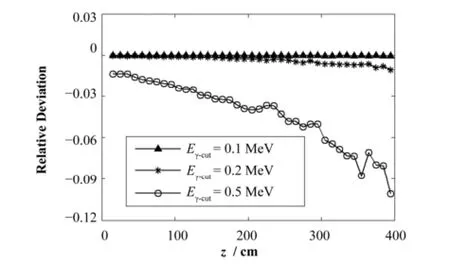
图4 不同γ截断能下的相对偏差Fig.4 Relative deviation under different effect of γ cut-off energy.
3 结语
对本工作,单板钴源辐照装置空场吸收剂量率MCNP模拟计算的总结:(1) 宜采用超线程模式下的并行计算,23个线程并行计算可将模拟耗时减小约13.1倍;(2) *F6记数方法适用于计算单板钴源辐照装置空场吸收剂量率,而*F8不适用;(3) 对于矩形空气记数栅元,栅元边长×度的值近似为常数(≈570),边长1cm的栅元,可在保证空间分辨率条件下获得模拟精度和平均相对偏差满意的模拟结果;(4) 相比γ截断能而言,电子截断能和γ致电子处理方式对计算效率的影响较大,采用γ输运模式(即模拟参数PHYS卡IDES=1)、100keV的γ截断能,可将模拟耗时进一步减小约4.4倍;(5) 不同因素对计算效率影响大小为:记数方法>并行线程数>栅元尺寸>电子截断能和γ致电子的处理方式>γ截断能。
综上,本工作在保证模拟精度(1%)和相对偏差(2%)的条件下将MCNP模拟耗时减小约57倍,获得了计算效率的提高。
1 郭平稳. Co-60辐照装置剂量场分布的计算与测量研究[D]. 长沙: 国防科学技术大学, 2004
GUO Pingwen. A study on computation an measurement of dose field distribution of Co-60 irradiation facility[D]. Changsha: National Defense Science and Technology University, 2004
2 刘江平.60Co辐照加工产品剂量分布的蒙特卡罗模拟[J]. 辐射研究与辐射工艺学报, 2010, 28(1): 57–61
LIU Jiangping. Monte Carlo simulation for the dose mapping of products irradiated by60Co γ-ray[J]. Journal of Radiation Research and Radiation Processing, 2010, 28(1): 57–61
3 Oliveira C, Ferreira L M, Gon-calves I F, et al. Monte Carlo studies of the irradiator geometry of the Portuguese gamma irradiation facility[J]. Radiation Physics and Chemistry, 2002, 65: 293–295
4 邱有恒, 应阳君, 王敏, 等. 光子能量沉积计算的一种新方法[J]. 原子核物理评论, 2011, 28(1): 97–102
QIU Youheng, YING Yangjun, WANG Min, et al. Several techniques on increasing computation efficiency of photon energy deposition[J]. Nuclear Physics Review, 2011, 28(1): 97–102
5 林辉, 吴宜灿, 陈义学. 基于临床实例的影响蒙特卡罗模拟程序MCNP计算精度和速度的若干参数模拟研究[J]. 原子核物理评论, 2006, 23(2): 237–241
LIN Hui, WU Yican, CHEN Yixue. Investigation of parameters influencing on simulation precision and speed of Monte Carlo MCNP based on a clinic case[J]. Nuclear Physics Review, 2006, 23(2): 237–241
6 GB 7465-2009, 高活度钴60密封放射源[S]. 2009 GB 7465-2009, High activity cobalt-60 sealed radioactive sources[S]. 2009
7 JJG 1028-1991, 使用重铬酸银剂量计测量γ射线水吸收剂量标准方法[S]. 1991
JJG 1028-1991, Standard method to measure γ-rays absorbed doses of water by sliver dichromate dosimeter[S]. 1991
8 GB/T15447-2008, X, γ射线和电子束辐照不同材料吸收剂量的换算方法[S]. 2008
GB/T15447-2008, Conversion method of absorbed doses in different material irradiated by X, γ rays and electron beams[S]. 2008
9 邓力, 张文勇, 徐涵, 等. 蒙特卡罗程序MCNPIIMCNP-5并行效率比较[J]. 计算机工程与科学, 2009, 31(A1): 185–187
DENG Li, ZHANG Wenyong, XU Han, et al. The comparison of parallel efficiency between Monte Carlo code MCNP-II and MCNP5[J]. Computer Engineering & Science, 2009, 31(A1): 185–187
10 王磊, 王侃, 余纲林. MCNP 程序并行计算性能分析[J]. 核科学与工程, 2006, 26(4): 301–306
WANG Lei, WANG Kan, YU Ganglin. Analysis of parallel computing performance of the code MCNP[J]. Chinese Journal of Nuclear Science and Engineering, 2006, 26(4): 301–306
11 X-5 Monte Carlo Team. MCNP-a general Monte Carlo n-particle transport code[R]. Version 5, LA-UR-03-1987, 2003
CLC TL929
Study on improving MCNP computational efficiency of dose rate for a single-rack cobalt irradiation facility
LI Lei LI Xiaoyan HUANG Wei JIANG Shubin WU Xiaoli YANG Guixia
(Institute of Nuclear Physics and Chemistry, Chinese Academy of Engineering Physics, Mianyang 621900, China)
Background: Monte Carlo method is regarded as the most accurate method for dose rate calculation at present, whereas its time-consuming defect increases complication for its application in industrial irradiation processing and experiment. Purpose: For a single-rack cobalt irradiation facility with loaded activity of 8.4PBq, a study of optimizing MCNP (Monte Carlo N Particle Transport Code) parameters was done to improve computational efficiency of dose rate. Methods: The effects of five parameters on MCNP computational efficiency, including the thread numbers of parallel computation, tally method, cell size, cutoff energy, and methods dealing with γ-induced electrons were discussed. Results: With certain precision and relative error, the least time-consuming situation was achieved with a set of five parameters, including parallel computation with hyper-thread mode, *F6 tally, cell size of 1cm, γ transport mode and γ-cutoff energy of 100keV. Conclusion: In this work, the cost of time was reduced about 57 times, and the improvement of MCNP computational efficiency was realized.
Single-rack cobalt irradiation facility, Absorbed dose rate, MCNP (Monte Carlo N Particle Transport Code), Computational efficiency
TL929
10.11889/j.0253-3219.2015.hjs.38.030201
李磊,男,1986年出生,2011年于四川大学获理学硕士学位,助理研究员,从事抗辐射加固及辐照工艺研究
2014-03-10,
2014-07-29