基于GA-BP神经网络系统的滚珠丝杠热误差建模

张辉杰 ，王 军,，吴文嘉，孙 军，舒启林

ZHANG Hui-jie1 , WANG Jun2,1, WU Wen-jia1, SUN Jun1, SHU Qi-lin2

（1.沈阳建筑大学 交通与机械工程学院，沈阳 110168；2.沈阳理工大学 机械工程学院，沈阳 110159）

0 引言

随着数控机床朝着高速化、精密化、自动化、智能化的方向发展，机床的零部件精度及装配精度都有很大改善，传统意义上的机床几何误差已经能得到较好的控制[1]。然而，机床运行时各零部件不可避免的产生温度变化，特别是进给系统的滚珠丝杠，其高速旋转，使轴承、丝杠螺母副摩擦产生大量热，导致丝杠产生轴向热变形，直接影响机床的定位精度。因此，研究丝杠的热误差建模方法，精确的预测其热误差，对提高数控机床的精度有着重要意义。

通常预测热误差的方法有线性回归法[2]、灰色理论[3]、BP神经网络[4]、RBF神经网络[5]等。这些方法的基本假设是：机床误差是与关键点的温度和位置有关的函数[6]。丝杠的热误差主要与螺母的实时位置和温度以及前后轴承的温度有关。获得这些信息后，可以建立一个丝杠的热误差模型。通过这个模型可以预测热误差，进而在加工过程中进行实时补偿，从而提高数控机床的加工精度。

其中，BP神经网络能充分逼近复杂的非线性关系，具有高度的鲁棒性和容错能力，广泛应用于热误差建模中，但是BP神经网络收敛速度慢，容易陷入局部极值[7]。针对上述问题，本文首先运用ANSYS软件对TX1600G镗铣加工中心进给系统的滚珠丝杠进行热特性分析，获得丝杠的温度和热误差数据，然后分别建立传统BP神经网络和GA-BP神经网络模型，对滚珠丝杠的轴向热误差进行建模，比较两种方法的预测效果。

1 滚珠丝杠的有限元分析

1.1 滚珠丝杠系统模型

滚珠丝杠具有高精度，高效率的特点，广泛应用于进给系统中[8]。TX1600G镗铣加工中心的滚珠丝杠系统主要由伺服电机、联轴器、前轴承支座、前轴承、滚珠丝杠、螺母、后轴承、后轴承支座等部分组成，如图1所示。

图1 滚珠丝杠系统三维简图

为了方便有限元分析，必须对有限元模型作出以下假设[9]：

1）忽略滚珠丝杠上的螺纹，倒角和退刀槽等对有限元分析影响较小的结构；

2）丝杠螺母副和轴承摩擦产生的热量恒定不变的；

3）对流换热系数是一个常数；

4）润滑剂对热传导的影响可以忽略不计。

1.2 轴承及丝杠螺母副的发热量计算[10,11]

滚动轴承的温度提高主要是由于滚动体和轨道摩擦引起的，其发热量计算公式为：

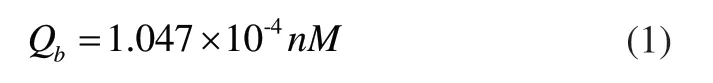
式中，Qb是轴承发热量(W)，n是轴承转速(rpm)，M是轴承的总摩擦力矩(N.mm)，由两部分组成：

式中，M1是与轴承所受载荷有关摩擦力矩，M2是与润滑剂粘度有关的摩擦力矩，其计算公式分别为：

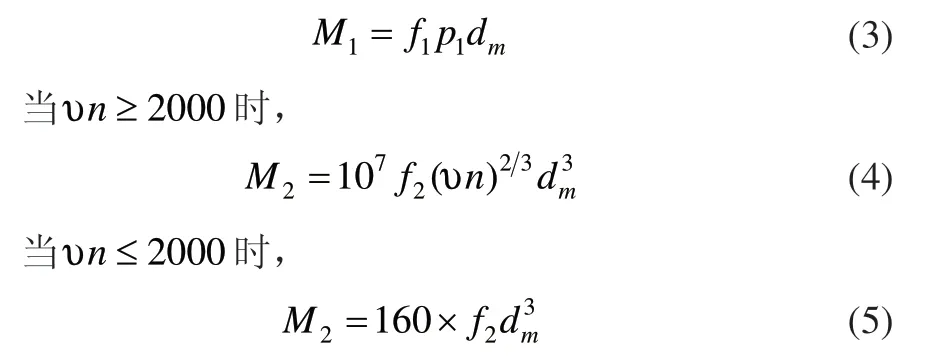
式(3)中，f1是与轴承类型和载荷有关的系数，p1是与轴承的预紧力(N)，dm是轴承的平均直径(mm)。

式(4)和式(5)中，f2是与轴承类型和润滑方式有关的系数，υ是润滑剂的运动粘度(mm2/s)。

滚珠丝杠螺母副发热量计算与轴承发热量相似，其计算公式为：

式(6)中，Qn是丝杠螺母副的发热量(W)，fn是与螺母类型和润滑方式有关的系数，υn是润滑剂的运动粘度(mm2/s)，nn是丝杠的转速(rpm)，Mn是螺母的总摩擦力矩(N.mm)。

1.3 热边界条件计算

丝杠表面与空气进行对流换热，根据努谢尔特准则，对流换热系数的计算公式为：

式中，Nμ是努谢尔特数，λ 是空气的热传导系数L是特征尺寸(mm)。

丝杠高速旋转，与周围空气强制对流换热，努谢尔特数计算公式为：

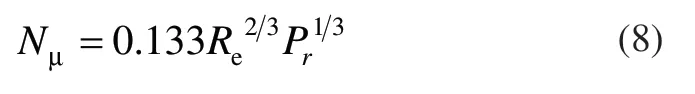
式中，Re是雷诺数，ω 是丝杠角速度(rad/s)，d是丝杠直径(mm)，υ是空气的运动粘度(mm2/s)，Pr是普朗特数。

1.4 建立模型及网格划分

为减少计算量，提高网格质量，将丝杠简化为阶梯光轴，利用ANSYS建立丝杠的三维模型，采用10节点四面体单元SOLID90进行网格划分。

1.5 温度场及热变形分析

滚珠丝杠的前端有四个相邻的滚动轴承，可简化为一个热源，后端两个轴承的位置是间隔的，看成是两个热源，将计算的热量转化为热流密度施加在滚珠丝杠的相应位置上。机床空载运行时，螺母在丝杠行程范围内往复移动。为模拟机床的实际运行条件，进行ANSYS仿真时，运用APDL语言在滚珠丝杠行程范围内施加往复移动的热流密度。在丝杠与空气接触的外表面节点上施加对流换热系数。

滚珠丝杠采用一端固定，一端自由游动的固定方式，丝杠的前端与联轴器相连，为完全约束状态，在丝杠的前轴承处施加X、Y、Z方向的位移约束，后轴承处施加X、Y方向的位移约束，再将仿真得到的温度场作为热载荷施加到丝杠上，求解得到滚珠丝杠的热变形云图。

设定丝杠转速为500rpm，环境温度为20℃，螺母循环运动6300s。6300s时丝杠的温度分布及热变形分布如图2所示。图3为前、后轴承和丝杠中心位置的温度变化曲线。图4为丝杠行程范围内各点随时间变化的轴向热误差曲面图，X轴表示丝杠行程范围内各点距离丝杠前端面的水平距离，Y轴表示时间，Z轴为轴向热误差。

图2 6300s时丝杠的温度场分布及热变形分布

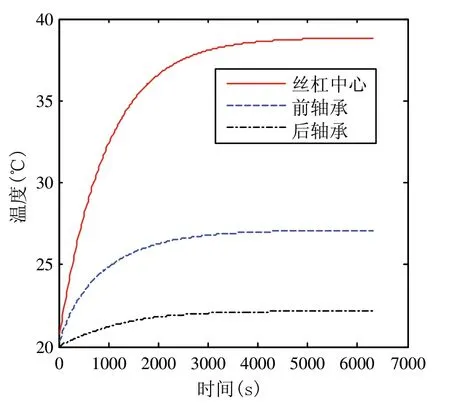
图3 温度变化曲线

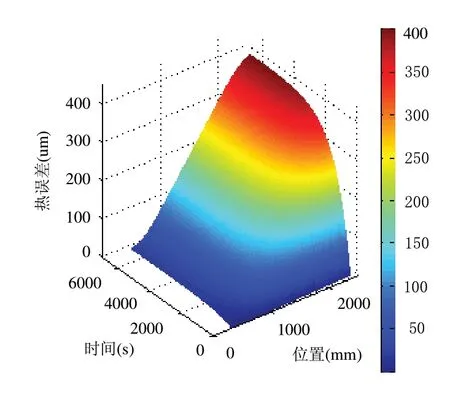
图4 滚珠丝杠轴向热误差的曲面图

由图2(a)和图3可知，随着仿真时间的增长滚珠丝杠温度越来越高，大约在3300s时丝杠达到热平衡状态，丝杠前端比后端温度略高。滚珠丝杠中间位置处温度最高，约为38.8℃，温升为18.8℃，前轴承处温度约为27.0℃，温升7.0℃，后轴承处温度最低约为22.1℃，温升2.1℃，温度场分布呈现中间高，两端低的特点。

由图2(b)和图4可知，越远离固定端，热变形越大，最大热变形出现在丝杠后端面，约为412μm。丝杠行程范围内的最大轴向热变形约为390μm。

2 GA-BP神经网络算法

2.1 GA-BP算法

遗传算法是一种通过模拟自然进化过程并行随机搜索最优解的方法。它把问题空间的参数转换成由一定结构的基因组成的个体，再按照所选择的适应度函数对个体进行选择、交叉、变异操作，保留适应度值好的染色体，组成新的种群，重新进行遗传操作，这样反复循环，直至寻得全局最优解。遗传算法具有较强的鲁棒性和普适性，适于并行处理，BP神经网络能较好的拟合非线性曲线，结合两者的优点，提出使用GA-BP模型进行误差建模。

GA-BP神经网络的算法流程由BP神经网络结构确定、遗传算法优化、BP神经网络预测3部分组成，如图5所示。

2.2 BP神经网络结构的确定

BP神经网络模型选用三层网络结构。输入层为前后轴承的温度、螺母的温度和位置以及环境温度，神经元个数为5；输出层为滚珠丝杠的轴向热变形，神经元个数为1；根据经验公式确定隐藏层神经元个数[10]，设为6。因此，确定BP神经网络模型为5-6-1网络结构，隐藏层传递函数使用tansig，输出层传递函数为purelin。

2.3 遗传算法优化

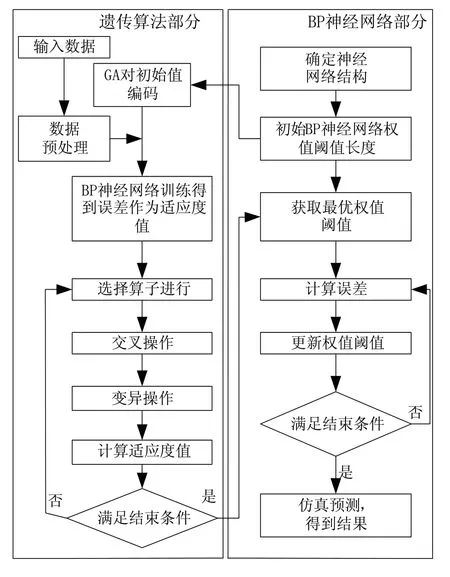
图5 算法流程

GA-BP模型通过优化BP神经网络的初始权值和阈值，更好地预测函数输出。GA-BP神经网络主要包括初始化种群、选择适应度函数、选择、交叉以及变异操作等要素。个体编码方式采用实数编码，每个个体均由4部分组成，分为输入层与隐藏层连接权值、隐藏层与输出层连接权值、隐藏层阈值以及输出层阈值。在已知个体编码和网络结构的情况下，就可以构成一个权值、阈值以及结构确定的神经网络[12]。

个体适应度值F为预测输出和期望输出的误差绝对值之和：

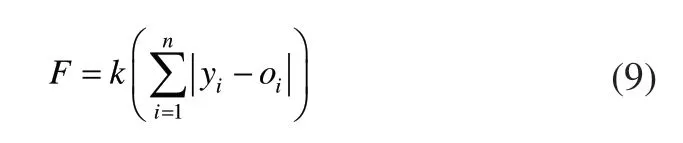
式中，k为系数，n为网络输出节点数，yi为BP神经网络第i个节点的期望输出，oi第i个节点的预测输出。

选择操作采用轮盘赌法，适应度值小的个体被选中的概率较大；交叉操作采用实数交叉法，将两个个体的部分编码互相交换；按变异概率对个体进行变异操作，按照遗传算法对个体进行寻优，直至寻得最优个体。

2.4 模型训练及预测

运用ANSYS每隔21s读取一次丝杠的温度场和热误差分析结果，共读取265组数据，其中215组数据用于网络训练，50组数据用于网络预测。设训练次数100次，预测精度为0.002，分别用传统BP网络模型和GA-BP网络模型对误差数据进行预测，比较两种模型的残余误差绝对值，结果如图6、图7及表1所示。

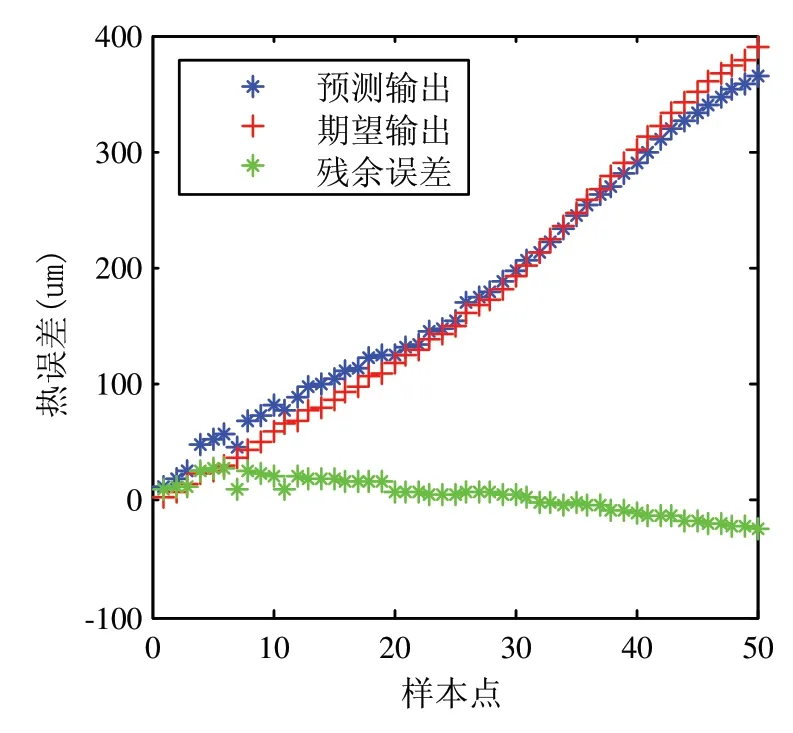
图6 传统BP网络模型

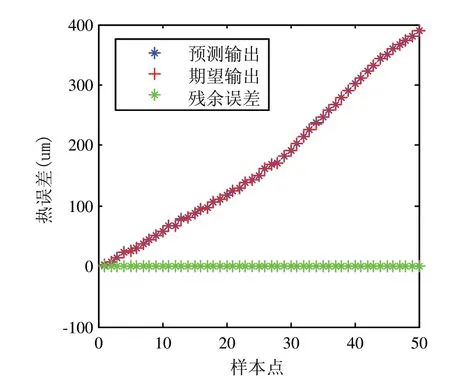
图7 GA-BP网络模型

表1 BP模型和GA-BP模型结果比较

由图6、图7及表1可知，达到相同的训练精度，GA-BP网络模型需要的训练次数少，残余误差绝对值小。因此，优化的BP网络模型训练时间短，拟合效果更好。

3 结论

1）本文运用FEM对TX1600G镗铣加工中心的滚珠丝杠进行热变形分析，获得丝杠转速为500rpm时的温度场分布和热变形规律，为进一步研究丝杠的热误差预测提供了理论基础。

2）通过MATLAB软件对有限元仿真得到的温度和热误差数据进行处理，先后运用传统的BP网络模型和GA-BP网络模型对丝杠的热误差进行预测，优化后的BP神经网络模型收敛速度快，预测精度高，对研究丝杠热误差的实时补偿具有一定的探索意义。

[1]姜辉,杨建国,姚晓栋,等.数控机床主轴热漂移误差基于贝叶斯推断的最小二乘支持向量机建模[J].机械工程学报,2013,49(15):115-121.

[2]Yang J G,Ren Y Q,Liu G L,et al.Testing,variable selecting and modeling of thermal errors on an INDEX-G200 turning center[J].The International Journal of Advanced Manufacturing Technology,2005,26(7-8):814-818.

[3]Yang H,Ni J.Adaptive model estimation of machine-tool thermal errors based on recursive dynamic modeling strategy[J].International Journal of Machine Tools and Manufacture,2005,45(1):1-11.

[4]Kang Y,Chang C W,Huang Y,et al.Modification of a neural network utilizing hybrid filters for the compensation of thermal deformation in machine tools[J].International Journal of Machine Tools and Manufacture,2007,47(2):376-387.

[5]Yang H,Fang H,Liu L,et al.Method of key thermal stiffness identification on a machine tool based on the thermal errors neural network prediction model[J].Jixie Gongcheng Xuebao(Chinese Journal of Mechanical Engineering),2011,47(11):117-124.

[6]靳增锋,王品.基于神经网络系统的滚珠丝杠热误差建模[J].组合机床与自动化加工技术,2012(1):1-4.

[7]王春暖,秦波,秦岩,等.基于改进PSO优化BP的数控机床热误差预测研究[J].组合机床与自动化加工技术,2014,10:020.

[8]李醒飞,董成军,陈诚,等.单热源作用下滚珠丝杠的温度场建模与热误差预测[J].光学精密工程,2012,20(2):337-343.

[9]Wu C H,Kung Y T.Thermal analysis for the feed drive system of a CNC machine center[J].International Journal of Machine Tools and Manufacture,2003,43(15):1521-1528.

[10]Xu Z Z,Liu X J,Kim H K,et al.Thermal error forecast and performance evaluation for an air-cooling ball screw system[J].International Journal of Machine Tools and Manufacture,2011,51(7):605-611.

[11]Xu Z Z,Liu X J,Choi C H,et al.A novel high speed/high precision ball screw[J].International Journal of Precision Engineering and Manufacturing,2013,14(1):165-167.

[12]史峰,王小川,郁磊,等.MATLAB神经网络30个案例分析[J].北京:北京航空航天大学出版社,2010.