一类非线性耦合波动方程组解的整体不存在性

裴金仙

（山西大学 商务学院，山西 太原030031）

本文主要研究带有源项和线性阻尼的非线性耦合波动方程组的初边值问题

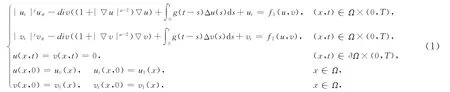
式中：Ω是Rn中具有光滑边界的有界区域，常数j＞0，α≥2，g，f1和f2是给定函数.

对于非线性偏微分方程的研究已经有两百多年的历史，对于具有很强实际背景的非线性发展方程的柯西问题和初边值问题解的性质的研究成了众多数学工作者的研究课题.对于线性以及非线性的弦振动系统、梁振动系统、膜振动系统等双曲型方程的解的适定性、整体存在性和解的整体不存在性的研究已有许多结果.Kafini和Tatar［1］研究了如下单个粘弹性波动方程的柯西问题，

得到了当初值在一个紧支集时，系统的一阶能量是多项式衰减的.

Messaoudi［2-3］研究了带有源项和粘弹性阻尼项的如下方程的Dirichlet问题，

其中，b=0或b=1，对于松弛函数g的条件假设，得到了问题的能量未必是指数稳定或者多项式稳定，而是与松弛函数的衰减类型相同的.之后，Liu［4］将类似的结果推广到负源项的情形.

关于抽象的粘弹性方程

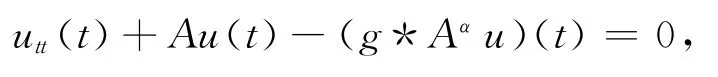
式中：A是一个定义在某个Hilbert空间的子集上的正定自伴算子；＊表示关于时间变量t的卷积.Rivera［5-6］证明了当参数α∈（0，1）时，即使松弛函数g指数衰减，系统的解只能是多项式衰减的；当参数α=1时，系统的解与松弛函数g具有相同的衰减性.

Cavalcanti等［7］研究了如下有界空间区域上的非线性波方程，得到了系统的指数衰减性.

近期，Mustafa［8］研究了在部分边界上具有粘弹性阻尼时的波动方程初边值问题，得到了显式的与松弛函数相关的一般衰减性结果.关于更多具有粘弹性阻尼的单个波动方程的性质的研究见文献［9-11］.

Arge和Rammaha［12］研究了如下有界空间区域上的波动方程组

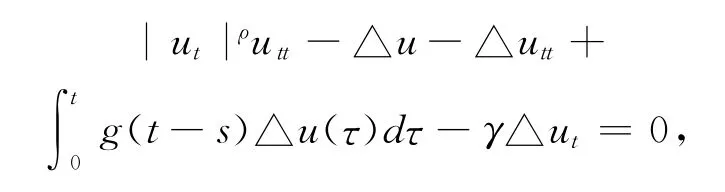
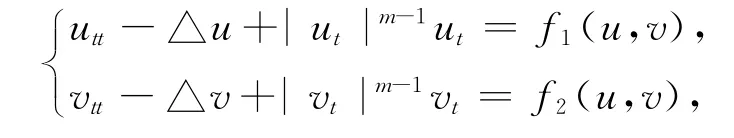
分别得到了弱解的整体存在性和弱解的有限时刻爆破等结果.

Mustafa［13］研究了如下有界空间区域上的波动方程组

证明了解的局部存在性，得到了解的稳定性结果.

Han和Wang［14］研究了如下有界空间区域上的波动方程组

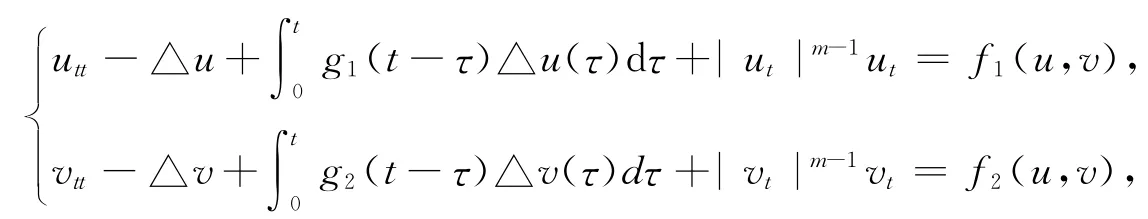
得到了系统的局部存在性、整体存在性以及解的爆破结果.

对于非线性波动方程的解而言，是整体存在还是在有限时刻发生爆破，取决于在一定的初始状态的条件下，源项和阻尼项作用的强弱.当阻尼项起的作用较大时，解是整体存在的；而当源项起的作用较大时，整体解将不存在（爆破将发生）.本文研究较一般化的问题（1），通过构造一个合适的泛函，对源项、粘性阻尼和弹性阻尼起的作用大小比较进而得到解的整体不存在性.由于这类问题具有振动现象的实际背景，因此对于这类问题的研究结果具有理论指导实际的意义.函数f1和f2形如?

其中，a和b为正常数，p满足

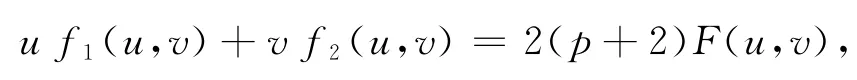
其中

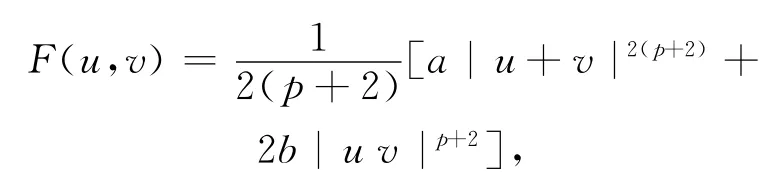
容易验证，存在正常数C0，C1使得

1 预备知识

假设函数g是非负不增的C1类函数，且满足

定义

经过求导计算可得

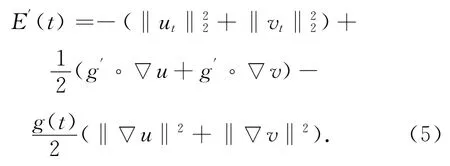
为方便记Lp（Ω）空间中的范数为：‖·‖p=‖·‖Lp（Ω），记‖·‖=‖·‖L2（Ω）.本文中，记C表示广义正常数.

2 解的整体不存在性

以下给出问题（1）解的爆破结果.

定理1 假设

则问题（1）的解不是整体存在的.

证明 为了证明整体解的不存在性，定义一个泛函L（t），通过证明L（t）满足微分不等式

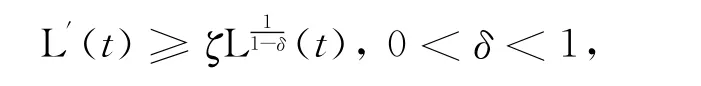
进而得到结果.

定义

则由式（5）及E（0）＜0可知，

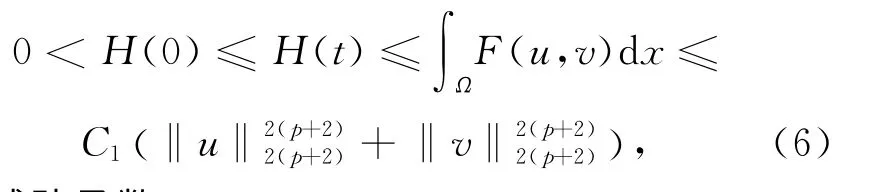
定义辅助函数

首先求导可得

利用Holder不等式，可得存在正常数λ＜p+2，

使得

因此，对于正常数γ∈（max｛α，2λ｝，2（p+2）），

式（8）可以写为

利用Young′s不等式，可知存在可以依赖于t的

函数ξ（t），使得

取

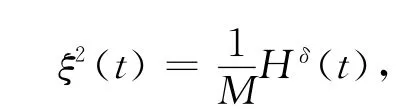
式中：M为待定正常数.

由于

进一步由嵌入定理知

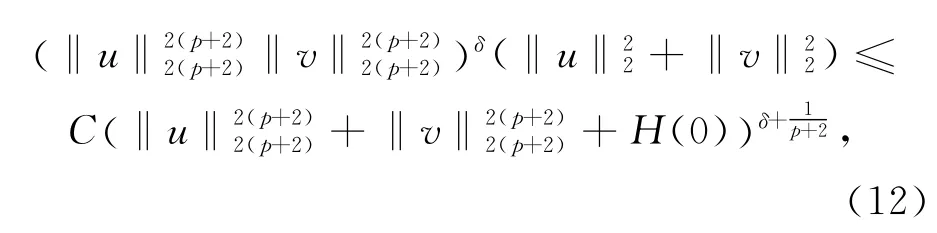
结合式（6）和如下不等式

可得

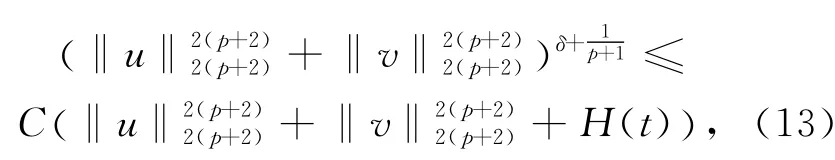
结合式（9）～式（13），有

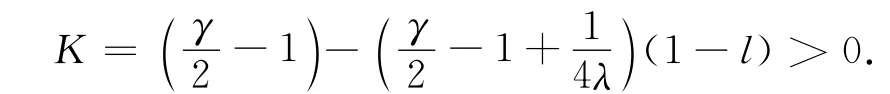
其中选取M＞0足够大，对于取定的M，再选取ε＞0足够小，则存在常数Λ＞0使得

选取ε充分小，可使

进而有

由于

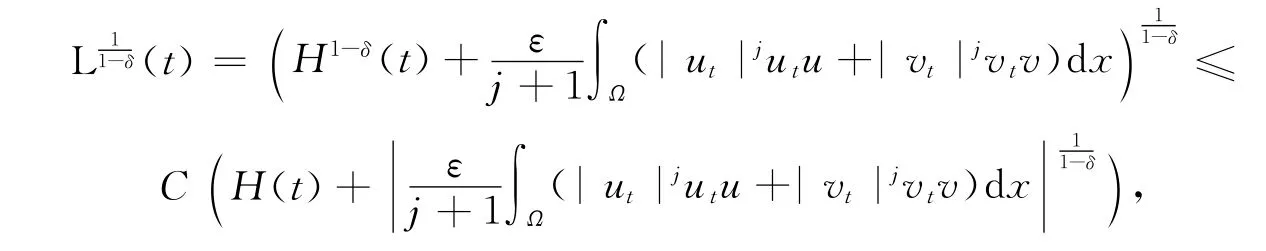
由Holder不等式和Young′s不等式，可得

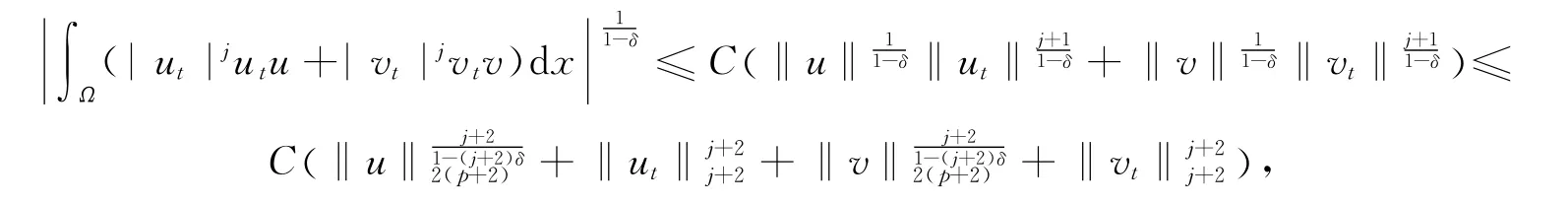
由于δ的选取以及式（6）可知

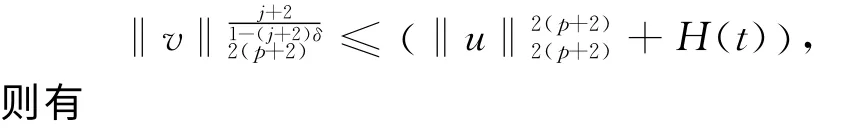
进而可得

结合式（15）和式（16）可得存在正常数γ，使得

求解这个微分不等式得到

因此，H（t）在有限时刻爆破，爆破时刻的上界估计为

定理1得证.

［1］Kafini M，Tatar N-e.A decay result to a viscoelastic in Rnwith an oscillating kernel［J］.J.Math.Phys.，2010，51：073506.

［2］Messaoudi S A.General decay of solutions of a viscoelastic equation［J］.J.Math.Anal.Appl.，2008，341：1457-1467.

［3］Messaoudi S A.General decay of the solution energy in a viscoelastic equation with a nonlinear source［J］.Nonlinear Anal.，2008，69：2589-2598.

［4］Liu W J.General decay of solutions of a nonlinear system of viscoelastic equations［J］.Acta Appl.Math.，2010，110：153-165.

［5］Munoz Rivera J E，Naso M G，Vegni F M.Asymptotic behavior of the energy for a class of weakly dissipative second-order systems with memory［J］.J.Math.Anal.Appl.，2003，286（2）：692-704.

［6］Munoz Rivera J E，Naso M G.On the decay of the energy for systems with memory and indefinite dissipation［J］.Asymptot.Anal.，2006，49：189-204.

［7］Cavalcanti M M，Domingos Cavalcanti V N，Ferreira J.Existence and uniform decay for nonlinear viscoelastic equation with strong damping［J］.Math.Meth.Appl.Sci.，2001，24：1043-1053.

［8］Mustafa M I.Uniform decay for wave equations with weakly dissipative boundary feedback［J］.Dyn.Syst.，2015，30（2）：241-250.

［9］Kafini M.On the uniform decay in Cauchy viscoelastic problems［J］.Afr.Mat.2012，23：85-97.

［10］Messaoudi S A.General decay of solutions of a weak viscoelastic equation［J］.Arab.J.Sci.Eng.，2011，36：1569-1579.

［11］Park J Y，Kang J R.Global existence and uniform decay for a nonlinear viscoelastics equation with damping［J］.Acta.Appl.Math，2010，110：1393-1406.

［12］Agre K，Rammaha M A.System of nonlinear wave equations damping and source terms［J］.Differ.Intrgral Equ.，2006，19：1235-1270.

［13］Mustafa M I.Well posedness and asymptotic behavior of a coupled system of nonlinear viscoelastic equations［J］.Nonlinear Anal.RWA，2012，13：452-463.

［14］Han X，Wang M.Global existence and blow-up of solutions for a system of nonlinear viscoelastic wave equations with damping and source［J］.Nonlinear Anal.TMA，2009，71：5427-5450.