基于正交试验法的冗余捷联惯组故障诊断实验方法研究*

王易南，罗 洋，尚妮妮，陈 凯，闫 杰

(西北工业大学航天学院，陕西 西安 710072)

运载火箭控制系统由测量设备和执行机构组成。新一代运载火箭控制系统采用了光学捷联惯组、光学速率陀螺、三冗余箭载计算机等。作为运载火箭重要的测量设备，捷联惯阻都采用了冗余配置来保证运载火箭控制系统的正常工作［1］。运载火箭普遍采用了三捷联惯组系统级冗余，采用三套惯组共架正交安装，如图1所示，通过三套惯组的输出值进行表决检测故障，并隔离故障惯组［2］。在对惯组的故障信号及输出形式分析研究的基础上，设计出各种不同类型故障检测算法，而对这些故障检测算法的有效性评估，以往采用大量重复性实验，不仅耗费大量时间还不能考虑到所有的故障情况。针对此缺陷，引入多因素、多水平正交试验来评估故障检测算法。

正交试验产生于20世纪20年代，由英国罗隆姆斯特率先采用，在大量实验中选择具有代表性的试验来进行田间试验;二战后英国率先出版了正交试验应用实例，介绍应用成果，很快被英美等国军事工业和科研部门所采用;20世纪60年代日本引入后编制成正交表加以普及;Yooyoung Lee和James J.Filliben等人将正交试验应用到虹膜识别系统，用于测试不同环境，不同的算法，个体特征差异，取样生物特征等不同因素对虹膜虹膜系统检测匹配结果的灵敏度影响［3］。

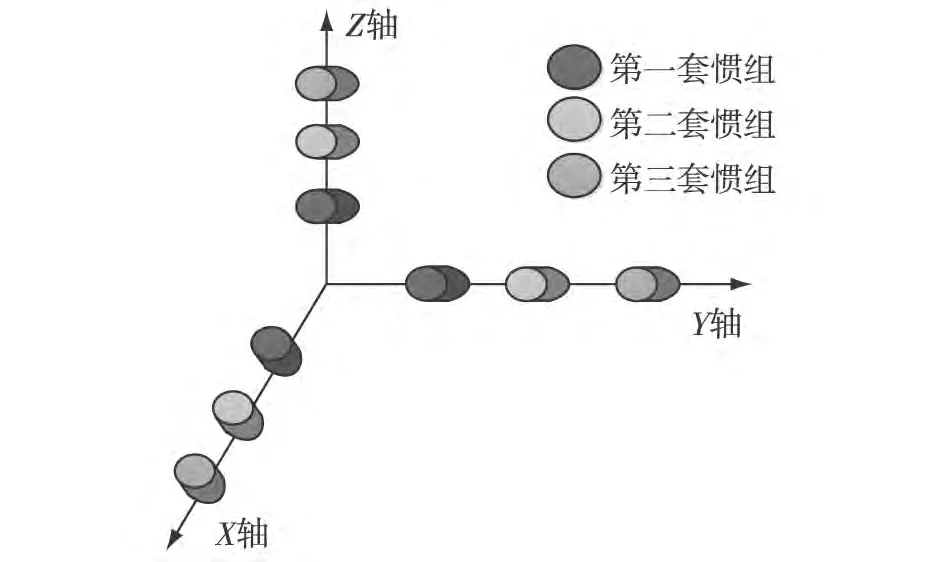
图1 三捷联配置图

国内广泛将正交试验应用与生产、科研实验。杨剑秋、王延容将正交试验应用到涡扇发动机空心风扇叶片的设计中，寻找帕累托最优解［4］;程文强在给出影响超然冲压发动机燃烧室性能的构型因素的基础上，应用正交试验相关理论，得到最优燃烧室构型［5］;华中科技大学熊军、侯俊佳等人对影响航天继电器触头弹跳的多因素进行了正交试验分析，采用的是基于方差分析的方法依次确定了影响触头弹跳的总弹跳时间指标、动触头最大动能、最大弹跳高度、最大动态接触力、最大冲击速度等指标的影响主次因素［6］。目前国内将正交试验大量应用于寻找最优参数或最优工艺，而很少将正交试验应用于性能测试。本文利用正交试验从大量的故障情况中选择具有代表性的故障状态进行实验安排，利用蒙特卡罗仿真测试捷联惯阻故障检测算法有效性。

1 正交试验

1.1 概述

正交试验设计法是研究与处理多因素、多水平试验的科学方法，根据正交性原理从全面试验中挑选出部分有代表性的试验点，这些试验点均衡地分布在整个试验范围内，每个试验点都有充分的代表性，如图2所示。这样，既能减少试验的次数，又能保证实验结果不受太大的影响，具有普遍代表性。

图2 正交试验点分布图

正交试验3个要素为:试验因素、因素水平、试验正交表。

1)因素。影响测试对象指标的可变的条件。本文在分析惯组的故障模型的基础上，考虑三捷联安装形式，影响故障检测算法检测效果的可变条件为故障幅值、轴向、惯组和故障类型，因此试验中以此4种条件为正交试验的因素。

2)水平。试验中，每个因素的不同的状态取值为水平。每种因素各有不同取值，这些不同的取值即为对应因素的水平。

3)正交表。运用数学组合理论在拉丁方和正交拉丁方的基础上构造而成的规格化表格。

1.2 捷联惯组故障正交试验表设计

本文是针对于冗余捷联惯组故障检测方法的实验研究，研究对象的配置方式选择为三套三正交捷联惯组。捷联惯组故障检测方法实验设计的具体流程如图3所示。以陀螺为例，研究分析建立其相应的正交试验表。

图3 捷联惯组故障检测实验方法

一般地，陀螺仪的误差模型描述如式(1)所示:

式中，b为陀螺零偏向量;ωbib为陀螺输入角速度向量;δAg为安装误差矩阵;ng为陀螺随机噪声向量;δKg为陀螺标度因子误差。

基于以上误差模型，建立陀螺故障类型和故障模型表，故障类型分为输出故障、参数故障零次项和参数故障标度因数3种类型，其中输出故障形式如表1所示;参数故障零次项输出形式如表2所示，参数故障标度因数输出形式与零次项类似。本文没有考虑陀螺的安装误差。

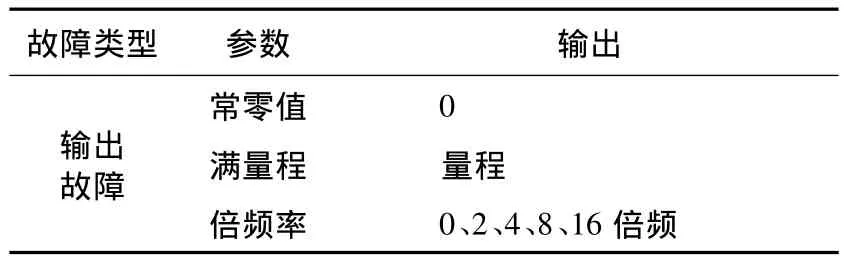
表1 陀螺输出故障表

表2 陀螺的参数故障零次项表

本文以三捷联配置中陀螺零次项常值和线性故障实验为例，考虑故障幅值(9水平)，轴向(3水平)，惯组(3水平)和故障类型(2水平)分别为试验因素，因素水平表如表3所示，采用正交表L54(92×321×2)安排试验，则建立其正交试验安排如表4所示(仅列出前27号试验)。

表3 三捷联陀螺零次项常值和线性故障水平表

表4 次项常值和线性试验安排表

至此，陀螺零次项常值和线性故障的正交试验安排表建立完成。研究确定正交仿真的试验设计指标，按照试验表的顺序依次进行试验，对于各种故障类型信号进行量化评估，进而评判故障检测方法的有效性。

2 设计试验指标及结果分析

2.1 试验结果

本文对表4所给出的试验安排共54个试验，每个实验进行1000次蒙特卡罗打靶，统计各个试验号下的故障检测结果，统计量为正检次数、误检次数、未检测次数，分别以3个统计量计算正检率、误检率和漏检测率。对表中54个试验安排中相同的试验安排求取平均，结果如表5所示。

表5 零次项常值和线性试验统计结果表

2.2 试验分析

本文采用极差分析法，对获得的实验数据进行分析，Ii为故障幅值因素为i水平下的试验结果累计平均;IIi为轴向因素为i水平下的试验结果累计平均;IIIi为惯组因素为i水平下的试验结果累计平均;IIIIi为故障类型因素为i水平下的试验结果累计平均。各因素的极差计算公式如下所示:

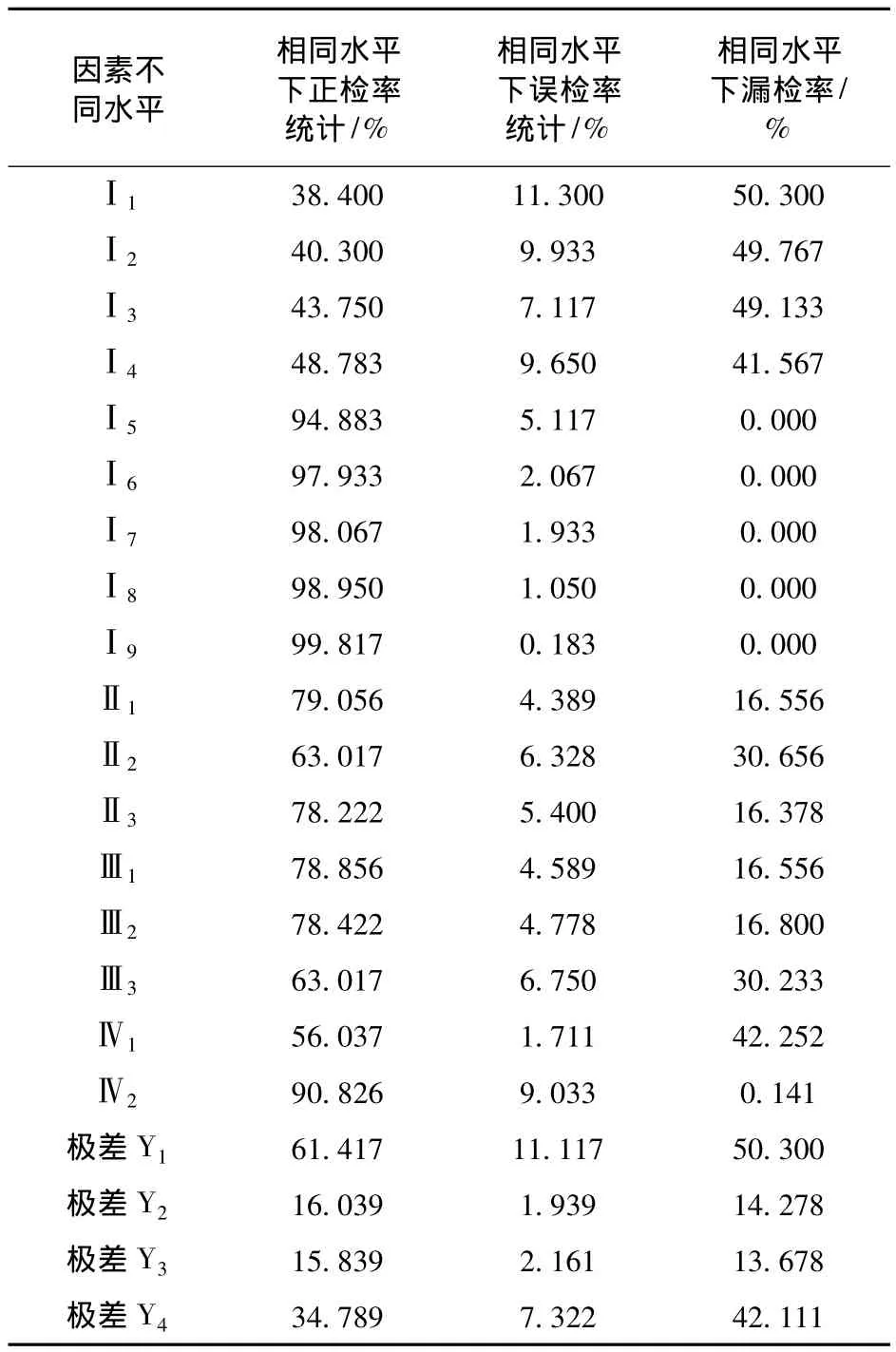
表6 零次项常值和线性试验极差分析表

由表6分析可知，三捷联惯组常值和线性故障实验中，对广义似然比故障检测算法的检测效果影响强弱依次为故障幅值、故障类型(常值还是线性)、轴向和惯组。由测试结果表5可知，线性故障比常值故障更容易检测;当故障幅值增加时故障检测算法正检率升高，误检率和漏检测率降低，当故障幅值增加到3°/h时故障检测算法的正确检测率达到90%以上。

3 结束语

本文针对以往关于捷联惯组故障诊断试验方法研究的缺陷与不足，提出运用正交试验来研究验证正交配置的捷联惯组的整机和器件的最主要的故障信号及其输出形式，并且在正交试验安排下测试故障检测方法。

试验结果表明:

1)正交试验能够很好地解决捷联惯组故障信号繁多，故障状态复杂的问题，并且大大减少了试验次数。文中若采用因素的所有水平组合排列出来的试验次数为9×3×3×2=192次试验安排，而采用正交试验安排试验，从所有的排列组合中选取了最优的最具代表性的试验共54次试验，由此看出大量减少了试验次数。

2)对广义似然比故障检测算法检测效果影响强弱的因素依次为故障幅值、故障类型、轴向和惯组。轴向和惯组对故障检测算法的影响相当。

3)故障幅值越大，故障检测算法效果越好，当幅值大于3°/h时故障检测算法正检率大于90%，在相同的故障幅值水平下，常值故障比线性故障更容易出现漏检，但是常值故障比线性故障误检率低，线性故障在故障幅值较小时表现出比常值故障更优异的检测性能。

4)正交试验作为一种试验方法可广泛应用于各个领域，尤其适用于一些工作量大，各因素间相互交联的试验情形。

5)本文目前仅考虑了正交试验研究捷联惯组故障信号及其对应的故障诊断方法具有很好的效果，但还未进行严格数学理论推导，证明其用于故障检测方法验证的最优性。

［1］ 中国宇航学会.航天科学技术学科发展报告［R］.北京:中国科学技术协会，2012-2013.

［2］ 李学峰.王青运载火箭飞行控制系统设计与验证［M］.北京:国防工业出版社，2014:35-62.

［3］ YooyoungLee，James J.Filliben.Sensitivity Analysis for Biometric Systems:A Methodology Based on Orthogonal Experiment Designs［J］，Computer Vision and Image Understanding，2013，117(5):532-550.

［4］ 杨剑秋，王延荣.基于正交实验设计的空心叶片结构设计［J］.航空动力学报，2011，26(2):376-384.

［5］ 陈文强.基于正交试验设计超然燃烧室数值模拟［D］.南昌:南昌航空大学，2013.

［6］ 基于正交实验设计的航天继电器触头弹跳的多因素分析［J］.电工技术报，2011，26(2):376-384.

［7］ Ron Patton.Software Testing［M］.Second Edition.北京:机械工业出版社，2006:216-230.

［8］ 于秀山.正交设计试验方法在测试用例设计中的应用［J］.计算机工程与应用，2004，20(1):62-63.

［9］ 方开泰，马长兴.正交与均匀试验设计［M］.北京:科学出版社，2001:15-20.