Effects of space and temperature dependent internal heat generation/absorption on MHD flow of a nanofluid over a stretching sheet*

GANGA B.， SARANYA S.， VISHNU GANESH N.， ABDUL HAKEEM A. K.. Department of Mathematics， Providence College for Women， Coonoor-643 04， India，E-mail： gangabhose@gmail.com. Department of Mathematics， Sri Ramakrishna Mission Vidyalaya， College of Arts and Science， Coimbatore-64 00， India

Effects of space and temperature dependent internal heat generation/absorption on MHD flow of a nanofluid over a stretching sheet*

GANGA B.1， SARANYA S.2， VISHNU GANESH N.2， ABDUL HAKEEM A. K.2
1. Department of Mathematics， Providence College for Women， Coonoor-643 104， India，E-mail： gangabhose@gmail.com
2. Department of Mathematics， Sri Ramakrishna Mission Vidyalaya， College of Arts and Science， Coimbatore-641 020， India

（Received February 4， 2014， Revised June 19， 2015）

In this paper we analyzed the effects of space and temperature dependent internal heat generation/absorption （non-uniform heat source/sink） on magnetohydrodynamic boundary layer flow of water based nanofluid over a stretching sheet with different nanoparticles. The flow is generated due to linear stretching of the sheet and influenced by uniform magnetic field， which is applied normally to the stretching sheet. A scaling group of transformation is used to reduce the governing momentum and energy equations into non-linear ordinary differential equations. The resulting differential equations are solved analytically using hypergeometric functions and numerically by the fourth order Runge-Kutta method with shooting technique. The influence of nanoparticle volume fraction， magnetic field， Prandtl number， non uniform heat source/sink， local skin friction coefficient and reduced Nusselt number are investigated for different nanoparticles.

nanofluid， MHD， heat generation/absorption， stretching sheet

Introduction0F

Nanofluids are suspensions of nanoparticles in fluids that show significant enhancement of their properties at modest nanoparticle concentrations. Many of the publications on nanofluids try to understand their behaviour so that they can be utilized where straight heat transfer enhancement is paramount as in many industrial applications， such as nuclear reactors，transportation， electronics as well as biomedicine and food. The broad range of current and future applications involving nanofluids has been given by Wong and Leon［1］. Nanofluids are not naturally occurring but they are synthesized in the laboratory. The thermal conductivity of these fluids plays an important role on the heat transfer coefficient between the heat transfer medium and the heat transfer surface. Therefore， numerous methods have been taken to improve the thermal conductivity of fluid by suspending nano/micro sized particles materials in base fluid such as oil，water and ethylene glycol mixture which are poor heat transfer fluids［2-5］.

The boundary layer flow over a continuously stretching surface finds many important applications in engineering processes， such as polymer extrusion， drawing of plastic films etc.. The boundary layer flow of nanofluids has been recently considered by several authors. Khan and Pop［6］analyzed the development of steady boundary layer flow， heat transfer and nanoparticle volume fraction over a linear stretching surface in a nanofluid. Kuznetsov and Nield［7］studied the classical problem of free convection boundary layer flow of a viscous and incompressible fluid past a vertical flat plate in the case of nanofluids.

Magnetic nanofluid is a colloidal suspension of carrier liquid and magnetic nanoparticles. The advantage of magnetic nanofluid is that fluid flow and heat transfer can be controlled by external magnetic field，which makes it applicable in various fields such as electronic packing， thermal engineering and aerospace.Effect of magnetic field on nanofluid convection in different geometries has been studied by several authors［8-10］. Hamad［11］has done work on an analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Vishnu Ganesh et al.［12］analyzed the effect of magnetic field on nanofluid flow over a stretching sheet numerically. Very recently， Vishnu Ganesh et al.［13］investigated the MHD flow of water based nanofluid over a stretching sheet with thermal radiation effect both analytically and numerically.

The effect of heat source/sink is very important in cooling process. Vajravelu et al.［14］have studied the convective heat transfer in the flow of viscous Agwater and Cu-water nanofluids over a stretching surface in the presence of uniform internal heat generation/ absorption. Abo-Eldahab and El Aziz［15］have investigated the effects of space dependent heat source/sink in addition to the temperature dependent heat source/ sink in the study of viscous flow. Very recently，Abdul Hakeem et al.［16］studied the effect of non uniform heat source/sink in a Walter's liquid B fluid over a stretching sheet with elastic deformation and thermal radiation effects. A close observation of the literature reveals that， to the best of the author's knowledge， so far no one has considered the effects of space and temperature dependent internal heat generation/absorption in nanofluids.

Keeping this in mind in this paper， we analysed the effects of space and temperature dependent internal heat generation/absorption on the boundary layer flow of a nanofluid over a stretching sheet in the presence of magnetic field both analytically and numerically.

Fig.1 Schematic of the physical model

1. Formulation of the problem

Consider the steady laminar two-dimensional flow of an incompressible viscous nanofluid past a linearly semi-infinite stretching sheet. We also consider a constant magnetic field strength B0which is applied normally to the sheet （see Fig.1）. The temperature at the stretching surface takes the valuewhile the ambient value， attained as y tends to infinity， takes the constant value T∞. The fluid is assumed to be a water based nanofluid containing different types of nanoparticles： Copper （Cu）， Silver （Ag）， Alumina（Al2O3）， and Titanium Oxide （TiO2） with internal heat generation/absorption. It is also assumed that the base fluid and the nanoparticles are in thermal equilibrium and no slip occurs between them. The thermos-physical properties of the nanofluid are considered as given in Vishnu Ganesh et al.［12］. Under the above assumptions， the boundary layer equations governing the flow and thermal fields can be written in the dimensional form as：

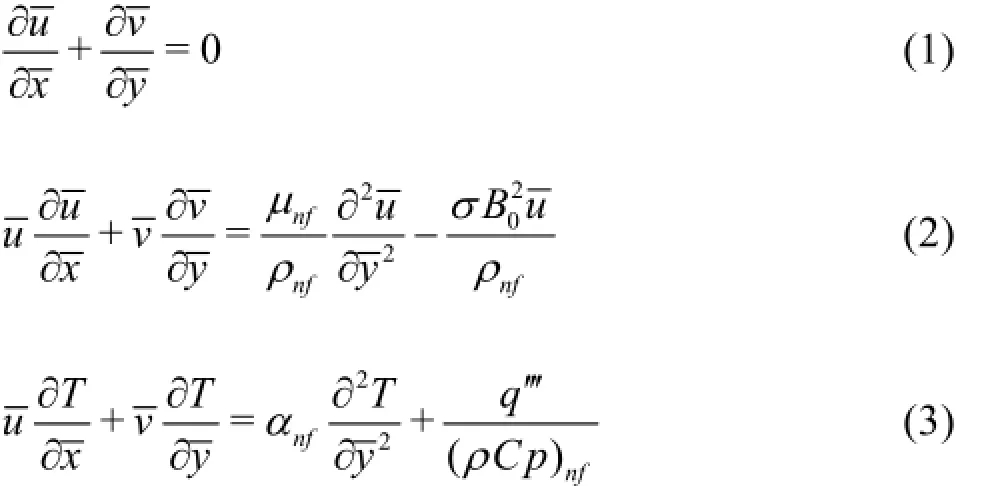
wherex is the coordinate along the sheet，uis the velocity component in thex direction，yis the coordinate perpendicular to the sheet，v is the velocity component in they direction，σis the electric conductivity，B0is the constant magnetic field strength， T is the local temperature of the fluid，αnf=knf/（ρCp）nfis the thermal diffusivity of the nanofluid andq′′is the space and temperature dependent internal heat generation（＞0）or absorption（＜0）（see also Abdul et al.［16］） which can be expressed for this problem as

here，A∗andB∗are parameters of space and temperature-dependent internal heat generation/absorption. It is to be noted that A∗＞0and B∗＞0correspond to internal heat generation while A∗＜0and B∗＜0 correspond to internal heat absorption. Therefore Eq.（3） is simplified to

where ρnfis the effective density of the nanofluid， µnfis the effective dynamic viscosity of the nanofluid，（ρCp）nfis the heat capacitance and knfis the thermal conductivity of the nanofluid， are given as：

here，φ is the solid volume fraction.

The boundary conditions of Eqs.（1）-（3） are

where µfis the dynamic viscosity of the basic fluid， ρfis the density of the pure fluid，（ρCp）fis the specific heat parameter of the base fluid，kfis the thermal conductivity of the base fluid，ρsis the density of the nanoparticles，（ρCp）sis the specific heat parameter of the nanoparticles，ksis the thermal conductivity of the nanoparticles andaandb are constants.

By introducing the following non-dimensional variables

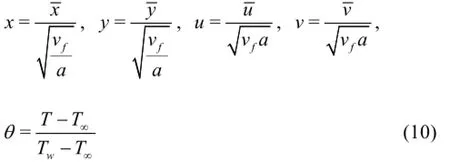
Equations （1）， （2） and （5） take the following nondimensional form

With the boundary conditions

where Pr=vf/αfis the Prandtl number and Mn=is the magnetic parameter.

By introducing the stream functionψ， which is defined as u=∂ψ/∂y and v=-∂ψ/∂x， then the Eqs.（12） and （13） become

and the corresponding boundary conditions （14） become

Now using the scaling group G of transformations， we get the scaling transformations as stated by Vishnu Ganesh et al.［12］

2. Solution of flow field

Now using the similarity transformations in Eq.（15）， we get

and the corresponding boundary conditions are

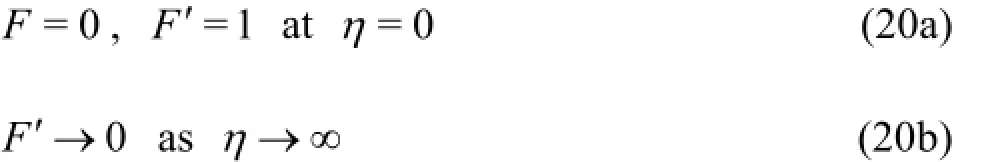
where the primes denote the differentiation with respect toη.

The exact solution to the differential Eq.（19） satisfying the boundary conditions （20） is obtained as

wherem is the parameter associated with the nanoparticle volume fraction， the fluid density and the nanoparticle density as follow

Thus the non-dimensional velocity components are

The dimensional velocity components are

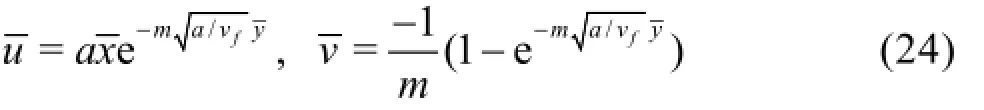
The shear stress at the stretching sheet characterized by the skin friction coefficient Cf， is given by

Using Eqs.（10）， （18）， （21）， （22） and （24）， the skin friction can be written as

3. Solution for the thermal transport

Substituting the similarity transformations （18） in（16）， we get

and the corresponding boundary conditions are

Now defining the new variable

Using Eqs.（21） and （29） in （27）， the governing equation for temperature can be put in the form

with the corresponding boundary conditions

where

The relation 4βB∗/m2≤p2must be satisfied in order to have real values ofq .

The solution of Eq.（30） with the corresponding boundary conditions in Eqs.（31） in terms ofηis obtained as

Dimensionless wall temperature gradient θ′（0） is obtained as

whereM is the hypergeometric function （Anjali devi and Ganga［17］） defined as following

The quantity of practical interest， in this section the Nusselt number Nuxis defined as

Using （10） and （18） we obtain the following Nusselt number

4. Numerical method for solution

The nonlinear coupled differential Eqs.（19） and（27） along with the boundary conditions （20） and （28）form a two point boundary value problem and is solved using shooting technique together with fourth order Runge-Kutta integration scheme by converting it into an initial value problem. In this method we have to choose a suitable finite value ofη→∞， say η∞. We set following first order system：

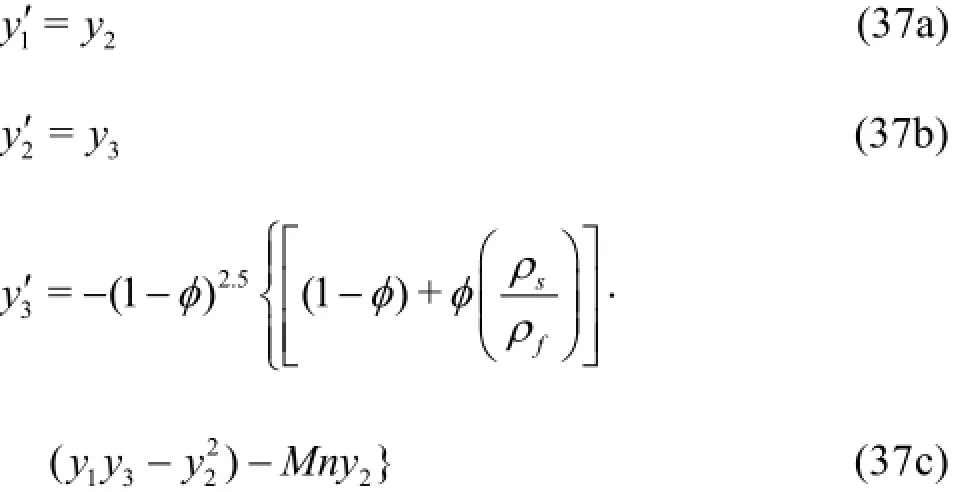
with the boundary conditions

To solve （37） with （38） as an initial value problem we need the values of y3（0）i.e.，F′′（0）and y5（0）i.e.，θ′（0）but no such values are given. The initial guess values for F′′（0）and θ′（0）are chosen and the fourth order Runge-Kutta integration scheme is applied to obtain the solution. Then we compare the calculated values of F′（η）and θ （η）at n∞with the given boundary conditions F′（η∞）=0and θ （η∞）=0， and adjust the values of F′′（0）and θ′（0）using shooting iteration technique to give better approximation for the solution. The process is repeated until we get the results correct up to the desired accuracy of 10-9level， which fulfils the convergence criterion.

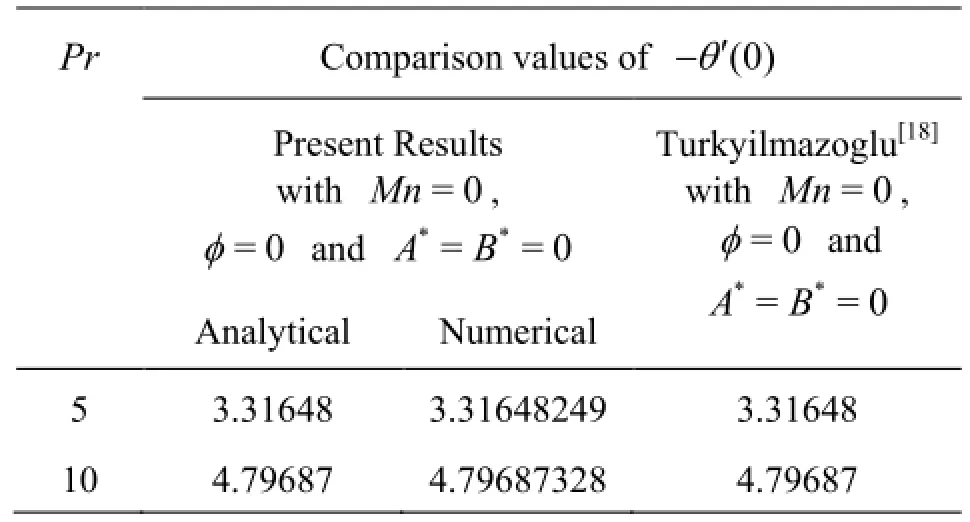
Table 1 Comparison of results for the reduced Nusselt number -θ′（0）

5. Results and discussion

In order to get the clear insight of the physical problem， the present results are discussed with the help of graphical illustrations for Al2O3-water. The effects of nanoparticle volume fraction， magnetic field，space and temperature dependent internal heat generation/absorption on velocity field and thermal field are discussed for the nanoparticles Cu， Ag， Al2O3and TiO2when the base fluid is water. The magnetic parameter（Mn）is varied from 0 to 6 and the nanoparticle volume fraction （φ） is varied from 0 to 0.2. The Prandtl number is fixed as 6.2 for base fluid water. In order to validate the present analytical and numerical results， we have compared our results with those of Turkyilmazoglu［18］for rated heat transfer -θ′（0）in the absence of nanoparticle volume fraction， magnetic parameter and internal heat generation/absorption. The comparisons in the above cases are found to be in excellent agreement as shown in Table 1.

Fig.2 Effect of Mn on velocity distribution F′（η）withφ= 0.2

5.1 Effects of physical parameters on velocity field

Figure 2 depicts the effect of magnetic parameter Mn on the transverse velocity F′（η）. It can be seen that the increasing values of magnetic parameter decrease the momentum boundary layer thickness. This is due to the intense amount of magnetic field inside the boundary layer increases the Lorentz force which significantly opposes the flow in reverse direction. Thus the increasing values of magnetic parameter cause the velocity of the fluid to decrease.

Fig.3 Velocity profiles for different types of nanofluids when φ=0.1，Mn=1

Figure 3 illustrates the effect of various nanoparticles on the nanofluid velocity. It is obvious that the different nanofluid has different velocity and also the velocity of Titanium Oxide nanofluid is higher than those of Copper， Silver and Aluminium Oxide nanofluids. The velocity field of the nanofluid depends onthe density of the nanoparticles. The velocity of the Silver-water is very low compared with others. This is due to the fact the density of the Silver is much higher than that of Cu， Al2O3and TiO2.

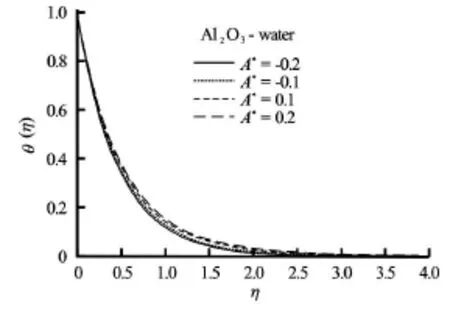
Fig.4 Effects of space dependent heat generation/absorbtion（A∗）on temperature distribution θ（ η）with φ=0.2，Mn =0.2，B∗=0.2and Pr=6.2

Fig.5 Effects of temperature dependent heat generation/absorbtion（B∗）on temperature distribution θ（ η）withφ= 0.2，Mn =2，A∗=0.2and Pr=6.2

Fig.6 Effect of φ on temperature distribution θ（ η）with space and temperature dependent heat generation/absorbtion，Mn =2and Pr=6.2

5.2 Effects of physical parameters on thermal field

Figures 4 and 5 display the effect of space and temperature dependent internal heat generation/absorption on the temperature field. It is clear that the increasing values of A∗（＞0）and B∗（＞0）lead to increase the thermal boundary layer thickness. This is expected since the presence of heat source （A∗＞0（Fig.4） and B∗＞0（Fig.5）） in the boundary layer generates energy which causes the temperature of the nanofluid to increase. This increase in the temperature produces an increase in the flow field due to the presence of nanoparticles. Heat sink （A∗＜0（Fig.4） and B∗＜0（Fig.5）） has an opposite effect which is cooling of the fluid， reducing the temperature in the boundary layer.

Fig.7 Effect ofMn on temperature distributionθspace and temperature dependent heat generation/absorbtion，φ= 0.2 and Pr=6.2

Fig.8 Effect ofPr on temperature distribution θ （η）space and temperature dependent heat generation/absorbtion，φ=0.2 and Mn=2

Figure 6 shows the effect of nanoparticle volume fraction （φ） with non uniform heat source/sink（A∗，B∗）on the temperature field. It is clear that the increasing values of nanoparticle volume fraction increase the thermal boundary layer thickness. Also it is noted that the same values of nanoparticle volume fraction has different effect on temperature in the presence of heat source/sink. In the presence of heat source（A∗＞0，B∗＞0）， the additional energy is generated in the boundary layer. The temperature increases withthe nanoparticle volume fraction. But in the case of heat sink （A∗＜0，B∗＜0） an amount of energy is observed from the boundary layer and the temperature get decreased.

Figures 7 and 8 reveal the effect of magnetic parameter（Mn）and Prandtl number（Pr）on thermal field. The increasing values ofMn cause the fluid to become warmer and therefore increase the temperature. The presence of magnetic field always increases the thermal boundary layer thickness. The increasing values of Prandtl number decrease the thermal field. Base fluids with lower Prandtl number have higher thermal conductivities （and thicker thermal boundary layer structures） so that heat can diffuse from the sheet faster than for fluids of higherPr （thinner boundary layers）. Hence Prandtl number can be used to increase the rate of cooling in conducting nanofluid flows. For the same values ofMnandPr the temperature increases or decreases according to the presence of heat source and sink.

Fig.9 Temperature profiles for different types of nanofluids when Pr =6.2，φ=0.2，Mn =2and A∗=B∗=0.2

Fig.10 Effect of the nano particle volume fractionφ on local skin friction coefficient

Figure 9 is plotted to get a clear idea about the nanoparticles on thermal field when the base fluid is water. This figure illustrates the effect of thermal conductivity of the nanoparticles on nanofluid thermal field. The temperature of the nanofluid with high thermal conductivity nanoparticles is higher than that of the nanofluid with low thermal conductivity nanoparticles. From Fig.9 it is clear that the thermal field is higher for Ag-water.

5.3 Effects on local skin friction coefficient and reduced Nusselt number

Figure 10 shows the variations of local skin friction coefficient versus the magnetic parameterMn for selected values of the nanoparticles volume parameter in the case of Al2O3-water. It is noticed that the change in the local skin friction to be higher for large values of φ when the value ofMnis small and for large value ofMn ， it is observed that the local skin friction decreases as φ increases. The values of reduced Nusselt number are presented in Table 2 for various values of physical parameters. It can be seen that the reduced Nusselt number decreases with the parametersMn，φ，A∗andB∗. The increasing values of the Prandtl number increase the rate of heat transfer. The values of reduced Nusselt number are maximum for TiO2-water and are minimum for Ag-water. The reduced Nusselt number of Al2O3-water is greater than Ag-water. The rate of heat transfer is higher for TiO2-water than others. This shows that the rate of heat transfer is influenced by the thermal conductivity of the nanoparticles.

6. Conclusions

An analysis has been carried out to study the effects of space and temperature dependent internal heat generation/absorption on the boundary layer flow of a water based nanofluid with various nanoparticles such as Cu， Ag， Al2O3and TiO2over a stretching sheet in the presence of magnetic field. The momentum and heat transfer equations are solved both analytically and numerically after converted into nonlinear ordinary differential equations by means of scaling transformations and the following results are obtained：

（1） The presence of the magnetic field decreases the velocity field. The velocity field is influenced by the density of the nanoparticles and the temperature of the nanofluid is influenced by the thermal conductivity of the nanoparticles.

（2） The increasing values of magnetic parameter increase the thermal field and the increasing values of Prandtl number shows an opposite effect on thermal field.

（3） The thermal field of nanofluid increases in the presence of space and temperature dependent heat source and decreases in the presence of heat sink.

（4） The local skin friction increases asMn increases with φ for small values ofMn， while for large values ofMn the local skin friction decreases as φ increases.

Table 2 Values of -θ′（0）for various values of governing parameters

（5） The reduced Nusselt number increases with the increasing values of magnetic parameter， non uniform heat sink parameter and nanoparticle volume fraction parameter and decreases with the increasing values of Prandtl number.

（6） The values of Nusselt number is maximum for TiO2-water and is minimum for Ag-water. The Nusselt number of Al2O3-water is greater than that of Ag-water. The rate of heat transfer is higher for TiO2than for others. This shows that the rate of heat transfer is influenced by the thermal conductivity of the nanoparticles.

Acknowledgements

The authors wish to express their sincere thanks to the honourable referees and the editor for their valuable comments and suggestions to improve the quality of the paper. One of the authors （N.V.G） gratefully acknowledges the financial support of Rajiv Gandhi National Fellowship （RGNF）， UGC， New Delhi， India for pursuing this work （Grant No. F1-17.1/2012-13/RGNF-2012-13-SC-TAM-16936）.

［1］ WONG K. F. V.， LEON O. D. Applications of nanofluids： Current and future［J］. Advances in Mechanical Engineering， 2010， 2（2）： 1652-1660.

［2］ DAS S. K.， CHOI S. U. S. and LI S. et al. Nanofluids：Science and technology［M］. Hoboken， New Jersey，USA： Wiley， 2007.

［3］ KAKAC S.， PRAMUANJAROENKIJ A. Review of convective heat transfer enhancement with nano fluids［J］. International Journal of Heat and Mass Transfer， 2009， 52（13）： 3187-3196.

［4］ WANG X.， MUJUMDAR A. S. A review of nano fluids-Part 1： Theoretical and numerical investigations［J］. Brazilian Journal of Chemical Engineering， 2008，25（4）： 613-630.

［5］ WANG X.， MUJUMDAR A. S. A review of nano fluids-Part 2： Experiments and applications［J］. Brazilian Journal of Chemical Engineering， 2008，25（4）： 631-648.

［6］ KHAN W. A.， POP I. Boundary layer flow of a nanofluid past a stretching sheet［J］. International Journal of Heat and Mass Transfer， 2010， 53（11）： 2477-2483.

［7］ KUZNETSOV A. V.， NIELD D. A. Natural convective boundary-layer flow of a nanofluid past a vertical plate［J］. International Journal of Thermal Sciences，2010， 49（2）： 243-247.

［8］ AMINOSSADATI S. M.， RAISI A. and GHASEMI B. Effects of magnetic field on nanofluid forced convection in a partially heated microchannel［J］. International Journal of Non-Linear Mechanics， 2011， 46（10）：1373-1382.

［9］ GHASEMI B.， AMINOSSADATI S. M. and RAISI A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure［J］. International Journal of Thermal Sciences， 2011， 50（9）： 1748-1756.

［10］ MAHMOUDI A. H.， POP I. and SHAHI M. Effect of magnetic field on natural convection in a triangular enclosure filled with nanofluid［J］. International Journal of Thermal Sciences， 2012， 59（2）： 126-140.

［11］ HAMAD M. A. A. Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field［J］. International Communications in Heat and Mass Transfer， 2011，38（4）： 487-492.

［12］ VISHNU GANESH N.， GANGA B. and ABDUL HAKEEM A. K. Lie symmetry group analysis of magnetic field effects on free convective flow of a nanofluid over a semi-infinite stretching sheet［J］. Journal of the Egyptian Mathematical Society， 2014， 22（2）： 304-310.

［13］ VISHNU GANESH N.， ABDUL HAKEEM A. K. and JAYAPRAKASH R. et al. Analytical and numerical studies on hydromagnetic flow of water based metal nanofuids over a stretching sheet with thermal radiation effect［J］. Journal of Nanofluids， 2014， 3（2）：154-161.

［14］ VAJRAVELU K.， PRASAD K. V. and LEE J. et al. Convective heat transfer in the flow of viscous Agwater and Cu-water nanofluids over a stretching surface［J］. International Journal of Thermal Sciences，2011， 50（5）： 843-851.

［15］ ABO-ELDAHAB E. M.， EL AZIZ M. A. Blowing/suction effect on hydro magnetic heat transfer by mixed convection from an inclined continuously stretching surface with internal heat generation/absorption［J］. International Journal of Thermal Sciences， 2004， 43（7）：709-719.

［16］ ABDUL HAKEEM A. K.， VISHNU GANESH N. and GANGA B. Effect of heat radiation in a Walter's liquid B fluid over a stretching sheet with non-uniform heat source/sink and elastic deformation［J］. Journal of King Saud University-Engineering Sciences， 2013， 26（2）：168-175.

［17］ ANJALI DEVI S. P.， GANGA B. Viscous dissipation effects on nonlinear MHD flow in a porous medium over a stretching porous surface［J］. International Journal of Applied Mathematics and Mechanics， 2009，5（7）： 45-59.

［18］ TURKYILMAZOGLU M. Analytic heat and mass transfer of the mixed hydrodynamic/thermal slip MHD viscous flow over a stretching sheet［J］. International Journal of Mechanical Sciences， 2011， 53（10）： 886-896.

* Biography： GANGA B. （1979-）， Female， Ph. D.，Assistant Professor

ABDUL HAKEEM A. K.，E-mail： abdulhakeem6@gmail.com