基于氡析出机制的铀矿井巷道通风可靠性分析

戴剑勇 石竞羽

基于氡析出机制的铀矿井巷道通风可靠性分析

戴剑勇1,2石竞羽1

1（南华大学 环境保护与安全工程学院 衡阳 421001）
2（南华大学 研究生处 衡阳 421001）

为解决铀矿放射性开采安全作业问题，氡的防护尤为重要，而氡运移规律及通风可靠性是解决防氡问题的基础，因此，研究铀矿氡迁移及通风可靠性具有重要的现实指导意义。本文以铀矿井巷道为研究对象，应用系统可靠性技术及氡析出机制，探讨氡在多孔介质中的渗流-扩散迁移规律，分析巷道内稳态和非稳态下氡的析出与分布，建立氡浓度安全作业条件下的铀矿井巷道通风可靠性模型，并利用MATLAB PDE工具箱开展了巷道氡迁移模拟及巷道通风可靠性数值分析，这为地下空间氡防护和铀矿井通风安全作业提供了参考依据。

氡析出，氡浓度，系统可靠性，数值模拟

地下铀矿山开采过程中会伴随着放射性污染物的析出与传播，氡及其子体对人体造成的危害引起了广泛的关注[1−2]。氡能够从射气介质表面析出进入井下空气中包括两个过程：镭原子发生α衰变时会放出一个α粒子并变成氡原子，自由移动的氡原子在介质孔隙和裂隙中通过扩散、渗流等机制向射气介质表面运移，最终离开射气介质表面进入周围空气[3−4]。氡的产生是连续的，在通风条件不好的空间，氡的浓度会达到很高。研究井下氡析出规律是研发防氡技术的基础，也是铀矿井实现安全、高效矿井通风的重要前提。井下空气中的氡析出量与矿井通风有密切的关系，通风压力、风压分布、风速及矿岩性质等都是影响氡析出量的因素[5−6]，这是氡有别于其他有害物的重要特性之一。通风不仅能够稀释和排除井下氡，降低氡浓度和氡子体α潜能，而且可以控制氡的析出，减少井下氡析出量。矿井中析出的氡一方面发生放射性衰变，另一方面随风流迁移，氡原子会因本身热运动，在体积活度梯度作用下从高浓度区域向低浓度区域扩散迁移。

谢东等[7−8]通过对放射性尾气在大气中扩散模拟，得出环境风速大小对核素氡的迁移有重要影响，排风口速度对核素氡的扩散有一定影响，并通过建立扩散模型，可预测铀矿放射性气体的迁移规律。此外，还有学者[9−10]开展了铀在固体介质中的扩散行为研究、地下留矿法铀矿采场的爆破铀矿堆内氡迁移和有限作业空间内氡浓度分布的影响研究。同时，为确保铀矿山井下放射性污染作业安全，许多专家学者提出了铀矿排氡及通风技术标准(EJ/T359-2006)及氡浓度在国家标准规定的限值内的概率[11]。此外，氡迁移动力学的偏微分方程求解问题是一热点和难点问题，而MATLAB强大的科学计算与图像可视化功能及在此基础上开发的偏微分方程工具箱(PDE Toolbox)，在环境安全工程领域中得到了广泛的应用[12−13]，且能够高效、灵活地解决这类复杂问题。本文应用可靠性技术，探讨氡的析出和传播规律，依据氡浓度限值概率，构建矿井氡浓度约束条件下安全生产作业可靠性模型，为强化铀矿井通风日常管理、减少事故发生提供重要参考价值。

1 氡析出与迁移传播机制

1.1 多孔射气介质表面氡析出

氡扩散迁移是指高浓度区域的氡向低浓度区域迁移。根据Fick第一扩散迁定律，对于岩体暴露表面来说，当以表面外法线方向为正方向时，由氡的扩散传播造成的氡通量J1为：

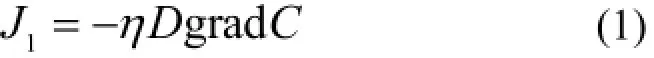
式中，gradC为沿ox方向的氡浓度梯度，Bq·m−4；D为氡在介质中扩散系数，m2·s−1；η为岩石孔隙度。

氡的被动传播由于压力梯度的缘故而产生渗流，氡的传播方向和速率都取决于流体。这时，当以岩石的外法线为正方向时，流过岩体表面的氡通量实际是流体渗流速率与流体中氡浓度的乘积。即：

式中，C为流体中的浓度，Bq·m−3；υ=−(k/μ)gradP，为流体的渗流速度，m·s−1。

1.2 射气介质中氡浓度分布方程

氡析出与氡浓度分布紧密相关，研究介质中氡浓度的分布是研究介质表面氡析出的基础。而矿井空气中的氡浓度不仅取决于氡的析出速率而且与风流流经巷道的距离有关。本文分别从氡在多孔射气介质中析出和氡穿过射气介质表面进入通风空间的传播两个过程分析氡的浓度分布。

巷道壁氡析出可近似看作为半无限大的问题。半无限大射气介质中氡传播问题是一维问题。巷道壁也可看作是均匀多孔射气介质，且介质的孔隙度、含铀品位、铀镭平衡系数、射气系数、渗透率、氡的扩散系数等皆为常数，故产生可移动氡的能力也为一常数。渗流速度大小和方向也是不随位置而变化的。半无限大射气介质中的氡的浓度分布计算坐标如图1所示。

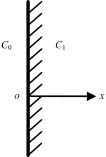
图1 射气介质计算坐标Fig.1 Emanation medium calculate coordinates.

垂直于介质表面沿深度设置计算坐标，取表面的内法线方向为正，介质中氡浓度稳定分布方程为：

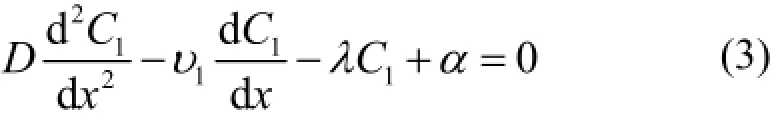
边界条件：x=0处，C1=ηC0；x→∞，C1=α/λ。式中，C1为介质中氡的视浓度；D为介质中氡的扩散系数；υ1为介质中的气体渗流速度；λ为氡的衰变常数；η为介质孔隙率；C0为介质外空间中的氡浓度；α为射气介质产生可移动氡的能力。此方程的解为：

巷道壁表面氡析出率为：

将式(4)代入式(5)即得：

2 氡浓度安全约束条件下的巷道型通风可靠性分析

2.1 巷道型通风空间氡浓度分布方程

为描述氡浓度沿巷道风流方向变化，假设如下：

(1) 一条均匀断面的巷道，截面积为S，m2；长，m；通风空间的容积V=S，m3。

(2) 氡析出均匀分布，巷道内氡析出密度ρ0稳定，即ρ0=J1L/S（L为巷道断面周长）为定值。风流中氡浓度变化计算如图2所示。

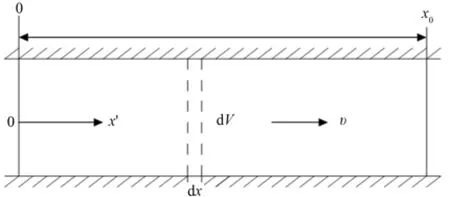
图2 巷道型通风空间氡浓度变化计算示意图Fig.2 Type of roadway ventilation space of variation of radon concentration calculation schematic.

沿巷道风流方向设置计算坐标，分析巷道中任意一个体积元dV中氡量的变化。风流流过此体积元后氡的增量来源于风流带入的氡和巷道空间析出的氡。

因此，在稳定状态下，体积元dV内氡量的变化为：

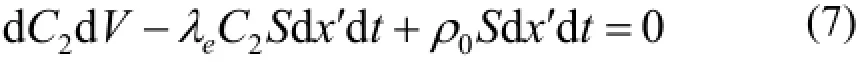
式中，x′分析的点距离巷道入风口的距离；C2为距离巷道入风口x′米处风流中的氡浓度；λe为氡的等效衰变常数。

若风流速度为υ2，风量Q=υ2S，通过的空气量与该体积元的体积相等，dV=Sυ2dt。

等式两边同除以Sdx′dt得：

因为巷道内的氡析出均匀，在x′=0处，C2=C'0，则巷道内氡析出的分布为：

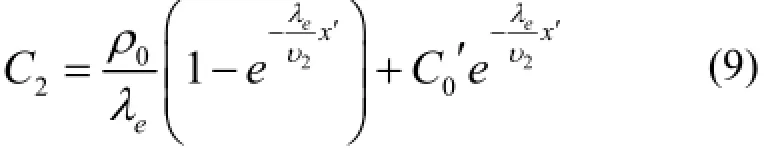
由于氡的衰变常数λ为2.1×10−6s−1，在地下矿山氡的等效衰变系数λe与衰变常数λ相差一般不超过10%，而巷道的长度也是有限的，满足x′=1时，′，于是巷道内氡浓度分布变形为：

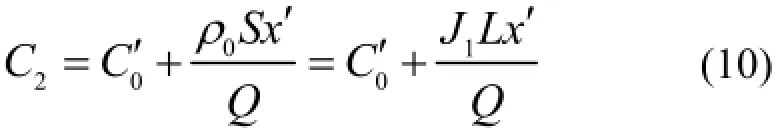
在不稳定的状态下，巷道内氡浓度随时间的变化的二维方程为：

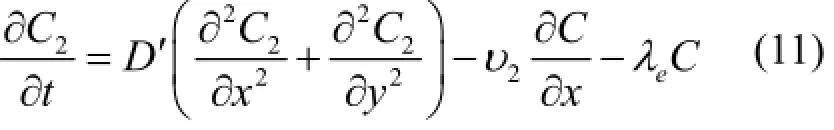
式中，D'为氡在巷道内的扩散系数。

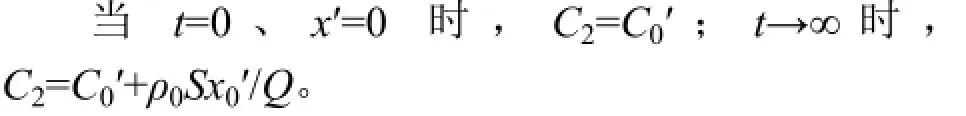
2.2 氡浓度控制条件下巷道通风可靠性模型构建

铀矿开采除一般金属矿山矽尘、有害气体危害外，还有放射性氡的危害，其对工作人员和公众产生的照射在核燃料循环中也是最大的。为了防止氡的危害和保护矿山工人的健康，必须使井下空气中氡浓度不超过国家标准规定的控制值，即氡浓度控制值为2.7 kBq·m−3。当氡浓度超过国家规定的浓度控制值时，对人体就是有害的，处于该环境巷道中作业是不可靠的。

根据氡在射气介质中的析出规律和在巷道空间扩散运移规律，得到巷道中氡浓度分布方程，可以看出射气介质中析出氡的速率和风流流经巷道的距离共同影响着氡浓度的分布。随着风流深入巷道的距离加大，风流中所含的氡浓度也不断增加。氡浓度在控制值之上时，距离入风口的距离占巷道全长的概率反映了巷道氡浓度的可靠程度。由此可以把巷道氡浓度可靠度定义为：在某一稳定状态下，在规定的时间内巷道中的风流氡浓度C2能够保持在管理限值Cp=2.7 kBq·m−3之下的任意位置在巷道总长中的比例，即X (C2≤Cp)的概率，称为该巷道的氡浓度可靠度，记为R。用公式表示为：

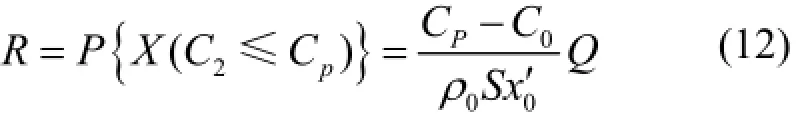
3 实例分析

某铀矿山断面均匀巷道长为70 m，宽为4 m，高为2.2 m，依据实际调查数据，巷道壁岩石孔隙率取0.3，矿石品位为0.11%，铀镭平衡系数为1.05，射气系数为0.12，矿石密度为2.9×103kg·m−3，矿石的平均直径为0.4 m。利用这些参数可以计算射气介质产生可移动氡的能力α=85.8 Bq·m−3·s−1，多孔介质的渗透率为1.78×10−11m2。空气粘滞系数取1.85×10−5Pa·s。

计算多孔射气介质中氡浓度分布，需要测量巷道内的氡浓度。然后利用式(3)的解计算出稳定状态下介质中氡浓度及巷道壁氡析出率J1。而一阶常微分方程(8)属于非刚性方程，利用MATLAB基于Runge-Kutta(4,5)法能够求解稳定状态下巷道内氡浓度分布方程(8)的初值。即通过调用函数ode45可求得稳定状态下巷道内氡浓度的数值解及分布图形。巷道氡浓度在稳定状态下的分布见图3。

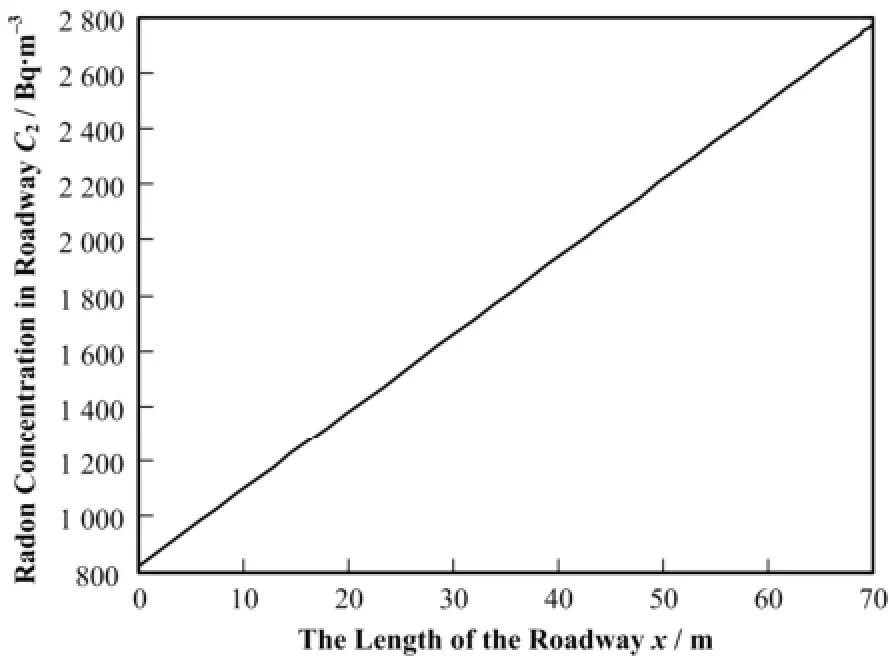
图3 稳定状态下巷道氡浓度分布Fig.3 Radon concentration distribution of roadway under the stable state.

由图3可见，巷道氡浓度与x′呈线性关系。巷道风流中氡浓度是随着风流流经巷道的距离而增大，风流末端总是最高氡浓度出现的地方。氡浓度增长也与巷道初始氡浓度、截面积、氡析出密度和风量有关。随着C0、ρ0和S而增大，随着Q的增大而减小。

非稳定状态下，巷道内氡浓度会随着通风时间而变化，应用MATLAB-PDE工具箱来求解氡浓度问题可简化编程难度，能够灵活地得到其解析解及可视化图形。其程序主要由确定几何区域和边界条件、初始化网络并加密、确定方程参数和结果可视化等部分组成。非稳定状态下巷道氡浓度分布方程属于抛物型方程，此方程参数设置为：c=0.0000045；a=0.0000021；f=237.3；d=1。初始条件：u0=820+27.7x。在时间段[0,1000]内取30个点，调用parabolic命令求解抛物型偏微分方程，最后绘制函数，可以获得氡浓度二维分布可视化图形(图4)。

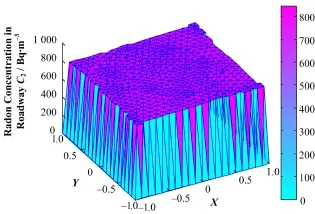
图4 Time=1000 s时巷道氡浓度二维分布Fig.4 Two-dimensional distribution of roadway radon concentration when time is 1000 s.

在通风初始阶段，巷道内氡浓度处于非稳定状态下，整个巷道中，距离介质表面同一深度处氡浓度几乎相等。巷道内的氡浓度都是随着风流流经的长度而增大，风量、截面积和氡析出密度都是其影响因素。

此外，根据系统初始条件已知C0=820 Bq·m−3，ρ0=7.8 Bq·m−3·s−1，Q=2.48 m3·s−1，S=2.2×4=8.8 m2，x0′=70 m，由式(12)计算可以得出巷道97.3%的地方氡浓度符合标准规定，该巷道的氡浓度可靠度较高，氡浓度控制得较好。

4 结语

通过对多孔射气介质中氡运移和巷道通风氡浓度的研究，获得了射气体内氡浓度分布规律，射气体表面的氡析出规律和巷道通风风流中氡浓度增长规律，并得出了巷道氡浓度可靠度，主要结论如下：

(1) 均匀多孔射气介质中氡浓度仅是距离介质表面深度的函数，越靠近介质表面氡浓度越大。

(2) 分析了在稳定状态下巷道内氡浓度与初始氡浓度、风量、氡析出密度、截面积以及风流流经长度等因素的相关性。无论是不稳定状态还是通风一段时间氡浓度达到稳定状态，巷道内氡浓度都是随着风流流经的长度而增加。

(3) 依据标准EJ/T359-2006规定了井下各工作场所空气中氡浓度控制值，定义了巷道氡浓度可靠度，并开展实例分析，求出了巷道氡浓度安全作业可靠度。

(4) 通过氡析出及迁移规律及巷道通风可靠度计算可获得铀矿井巷道通风降氡的关键措施。如采用正压通风、利用一些防氡涂料喷涂巷道壁及选取经济技术合理的风量等。

1 Darby S, Hill D, Auvinen A, et al. Radon in homes and risk of lung cancer collaborative analysis of individual data from 13 European case-control studies[J]. British Medical Journal, 2005, 330: 223−226

2 Krewski D, Lubin J, Zielinski J, et al. Residential radon and risk of lung cancer a combined analysis of 7 North American case control studies[J]. Epidemiology, 2005, 16(2): 137−145

3 程冠, 程建平, 郭秋菊. 土壤氡析出率影响因素及估算模型[J]. 环境放射性, 2006, 26(5): 520−524

CHENG Guan, CHENG Jianping, GUO Qiuju. The factors of soil radon exhalation influencing rate and estimation model[J]. Environmental Radioactivity, 2006, 26(5): 520−524

4 Semkow T M, Parekh P P. The role of radium distribution and porosity in radon emanation from solids[J]. Geophysical Research Letters, 1990, 17(6): 837−840

5 张哲, 朱民安, 张永祥. 地下工程与人居环境氡防护技术[M]. 北京: 原子能出版社, 2010

ZHANG Zhe, ZHU Min'an, ZHANG Yongxiang. Underground engineering and environment radon protection technology[M]. Beijing: Atomic Energy Press, 2010

6 Notley K R. Occupational radiation safety in mining proceedings of international conference[C]. Toronto: H, Stocke, 1984

7 谢东, 王汉青, 刘泽华, 等. 铀矿通风尾气中气态放射性核素氡大气扩散数值模拟[J]. 中南大学学报, 2013, 44(3): 213−223

XIE Dong, WANG Hanqing, LIU Zehua, et al. Numerical simulation of atmospheric dispersion of gas radioactive nuclides radon from uranium ventilation shaft exhaust[J]. Journal of Central South University, 2013, 44(3): 213−223

8 刘振昊, 彭小勇, 熊军, 等. 平地型铀尾矿库氡大气扩散数值模拟及环境效应分析[J]. 安全与环境学报, 2012, 12(3): 93−96

LIU Zhenhao, PENG Xiaoyong, XIONG Jun, et al. Simulation of atmospheric dispersion of radon from the flat type uranium tailings and analysis of environmental effects[J]. Safety and Environment, 2012, 12(3): 93−96

9 柏云, 帅正清, 朱晓红, 等. 铀在固体介质中的扩散行为研究[J]. 核技术, 2011, 34(11): 842−844

BAI Yun, SHUAI Zhengqing, ZHU Xiaohong, et al. Investigation on migration of uranium in solidified materials[J]. Nuclear Techniques, 2011, 34(11): 842−844

10 叶勇军, 丁德馨, 周星火, 等. 铀矿山地下留矿法采场内氡运移的数值模拟[J]. 铀矿冶, 2011, 2(4): 111−115

YE Yongjun, DING Dexin, ZHOU Xinghuo, et al. Numerical simulation on migration of radon in shrinkage stope underground uranium mines[J]. Uranium Mining and Metallurgy, 2011, 2(4): 111−115

11 周星火, 邓文辉, 吴钢, 等. 铀矿排氡及通风技术标准(EJ/T359-2006)[S]. 北京: 国防科学技术工业委员会, 2007

ZHOU Xinghuo, DENG Wenhui, WU Gang, et al. Technical regulations for radon exhaustion and ventilation in underground uranium mine(EJ/T359-2006)[S]. Beijing: Commission on Science, Technology, and Industry for National Defense, 2007

12 张敏, 余震果. 用MATLAB PDE工具箱解地下水稳定流问题[J]. 地下水, 2013, 35(1): 12−13

ZHANG Min, YU Zhenguo. Using MATLAB PDE toolbox solve the problem of steady flow of groundwater[J]. Ground Water, 2013, 35(1): 12−13

13 陆晨, 陈玉娟. 用MATLAB模拟几类非线性偏微分方程组的定性性质[J]. 牡丹江大学学报, 2013, 22(7): 131−135

LU Chen, CHEN Yujuan. Simulation qualitative property of several classes of nonlinear partial differential equations using MATLAB[J]. Journal of Mudanjiang University, 2013, 22(7): 131−135

CLC TL99, X591

Reliability analysis of tunnel ventilation based on the mechanism of radon exhalation in uranium mine

DAI Jianyong1,2SHI Jingyu1
1(School of Environmental and Safety Engineering, University of South China, Hengyang 421001, China) 2(The Graduate School of University of South China, Hengyang 421001, China)

Background: Radon protection is particularly important in underground uranium mining, and the migration regularity of radon and radon ventilation reliability are the base to solve the problem. Therefore, it is of practical significance to study the reliability of ventilation of uranium and radon migration. Purpose: The aim is to explore the radon diffusion regularity of seepage in porous media with system reliability and mechanism of radon exhalation. Methods: The exhalation and distribution of radon in the tunnel under the steady state and unsteady state were analyzed and the numerical simulation of the tunnel for radon migration was developed using MATLAB PDE toolbox. Results: Radon concentration within the tunnel increased with the length of flowing under both unstable and stable conditions with a period of time of ventilation. Calculation of reliability of tunnel based on the mechanism of radon exhalation reflected the exhalation and distribution of radon concentration of tunnel well. Conclusion: The results show that the understanding of the law on the radon exhalation provides reference for radon-prevention in underground space and ventilation and safe operation of uranium mine.

Radon exhalation, Radon concentration, System reliability, Numerical simulation

TL99，X591

10.11889/j.0253-3219.2015.hjs.38.010206

项目(No.51174116)、湖南省自然科学基金研发项目(No.10JJ2041)资助

戴剑勇，男，1969年出生，2006年于南华大学获硕士学位，现为博士研究生，研究方向为核安全系统工程

石竞羽，E-mail: 846116612@qq.com

2014-07-22，

2014-09-27