基于灰色聚类分析的教师课堂教学测评模型

臧传芹，谢孔峰

（中国人民解放军防化学院，北京 102205）

基于灰色聚类分析的教师课堂教学测评模型

臧传芹，谢孔峰

（中国人民解放军防化学院，北京 102205）

通过问卷调查，得到十名教师在课堂教学上的主观评分.如果只是通过计算教师课堂教学测评的平均分，不能客观真实地反映教师的实际教学效果.因此，采用灰色聚类分析方法，并运用MATLAB编程实现算法，将这十名教师按照课堂教学评价的优秀、良好、不合格分类.这种方法为建立一套合理、公正而有效的高校教师评价指标体系有探索意义.

matlab；灰色聚类分析；教学测评；主观评价

教师课堂教学测评是指通过不同的指标、不同的测评者来对被测评对象——教师的教学态度、手段、质量、效果等做一个科学的解读.目前，对教师课堂教学的评价方法有很多.常用的一种是由评价人员依据《课堂教学质量评价标准表》里的各项指标打分，再根据平均分的高低来排名，但这种评价方法不能反映教师的个性.因此，在实际评价问题中这种评价方式往往不能服众.

在本文中，教师课堂教学测评的主观评分是由选修过该教师课程的学生给出的，属于课堂教学评价中的内部评价.由于课程有难易，学生的评分是一个主观心理量，属于不确定性问题.因此，可以把这个评价问题视为一个“缺数据，少信息”的灰色系统.

1 灰色聚类分析方法

灰色系统理论是一种通过数据寻找数据的方法.它以“部分信息已知，部分信息未知”的系统为研究对象，处理小样本、缺数据、少信息的不确定性问题.灰色系统理论主要通过对系统内已知的部分原始信息进行加工、整理，完成对整个系统运动规律的正确描述和有效预测.经过近三十年的发展，灰色系统理论已发展为常用的处理不确定系统的方法之一，其广泛应用在经济、社会、农业、生物等研究领域中.

灰色聚类分析是灰色系统理论中的一种分析方法，主要包含两类：基于灰色关联度的聚类分析和基于灰色白化权函数的聚类分析方法.本文采用的就是基于灰色白化权函数的聚类方法，该方法广泛的应用于研究评价对象或指标的分类问题.

2 高校教师课堂教学评价指标体系的建立

由于本次测评是对课堂教学进行测评，因此在选择指标体系时，以有效组织课堂教学为根本目标.我们适当选取范辉君在《教学质量视角下高职教师评价体系研究》[6]一文中所建立的评价体系中关于课堂教学的评价指标.主要包括：①教师授课认真；②教师对课程精心准备；③教师对基本概念、原理的表达清晰；④教师授课内容设计合理；⑤教师授课进度适中；⑥教师授课内容难易适中；⑦教师讲课语言生动、形象；⑧教师书本知识传授严谨准确，无科学性错误；⑨教师课堂教学互动性强；⑩教师善于启发性教学；⑪教师激发学生兴趣，参与课堂讨论；⑫教师注重培养学生逻辑思维的能力；⑬教师注重培养学生自主学习能力；⑭教师注重培养学生独立思考的能力；⑮教师充分尊重学生的个性、学习习惯；⑯教师课堂上能进行科学有效的练习，巩固学习效果；⑰作业与考试内容覆盖教学重点、难点；⑱教师板书设计科学、精炼，富有审美性；⑲教师课堂上能渗透本学科的最新发展.

3 灰色聚类分析的步骤

将这n名要综合评价的教师记为聚类对象，m项评价指标记为聚类指标，根据n名教师关于m项聚类指标的取值相应的分成k个灰类.具体步骤如下：

（1）将第i名教师的第j项评价指标的得分记为xij(i=1, 2,…,n；j=1,2,…,m)，则n名教师的得分构成矩阵X,

（2）将n名教师关于聚类指标j的取值相应地分为k个灰类(这里是指：优秀、良好，不合格；k=1,2,3)，称为j指标子类；设λjk为第j个聚类指标k子类临界值，并按式（2）计算j指标关于k子类的权系数ηjk.

（4）确定第j个评价指标对第k个灰类的白化权函数fjk(x)：

定义第j个评价指标对教学质量不合格的白化权函数为

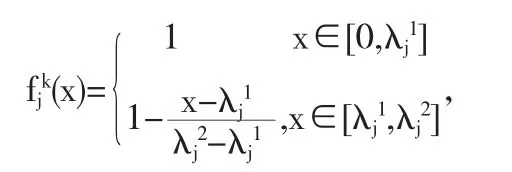
第j个评价指标对教学质量良好的白化权函数为

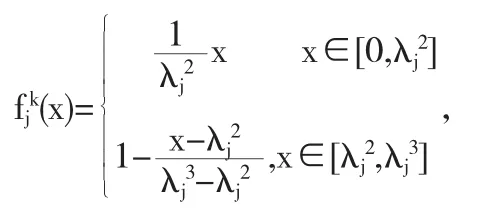
第j个评价指标对教学质量优秀的白化权函数为

（5）根据j聚类指标k子类的白化权函数和权系数，按照式（3）确定第i名教师属于k个灰类的灰色聚类系数αik.

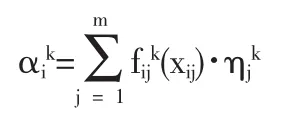
（6）构造第i名教师的灰色聚类向量αik(αi1,αi2,αi3)，列出聚类系数矩阵(σik)n×3.

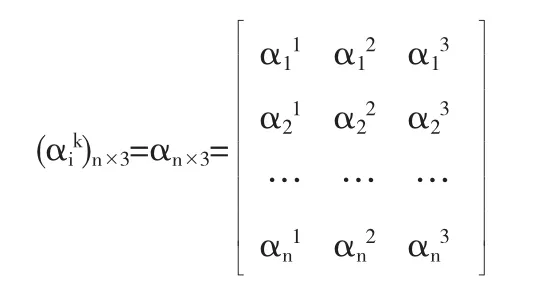
（7）确定第i名教师属于哪个灰类.在式（4）中，第i行的3个数值αi1,αi2,αi3对应着对第i名教师教学质量的综合评价属于优秀、良好、不合格这三个灰类的可能性大小.如果αi1最大，则说明第i名教师的综合评价属于教学质量优秀的一类；如果αi2最大，说明第i名教师的综合评价属于教学质量良好的一类；如果αi3最大，则说明第i名教师的综合评价为教学质量不合格的一类.

4 应用与结果分析

首先，随机抽取10名学生对7名教师的课堂教学打分，打分时采用数字型标尺（1分表示非常差，7分表示非常好），得到10份打分表.对每名教师，取每项评价指标分数值的众数，将其绘制成一张新表，来分析每个主观评分数据的集中趋势.

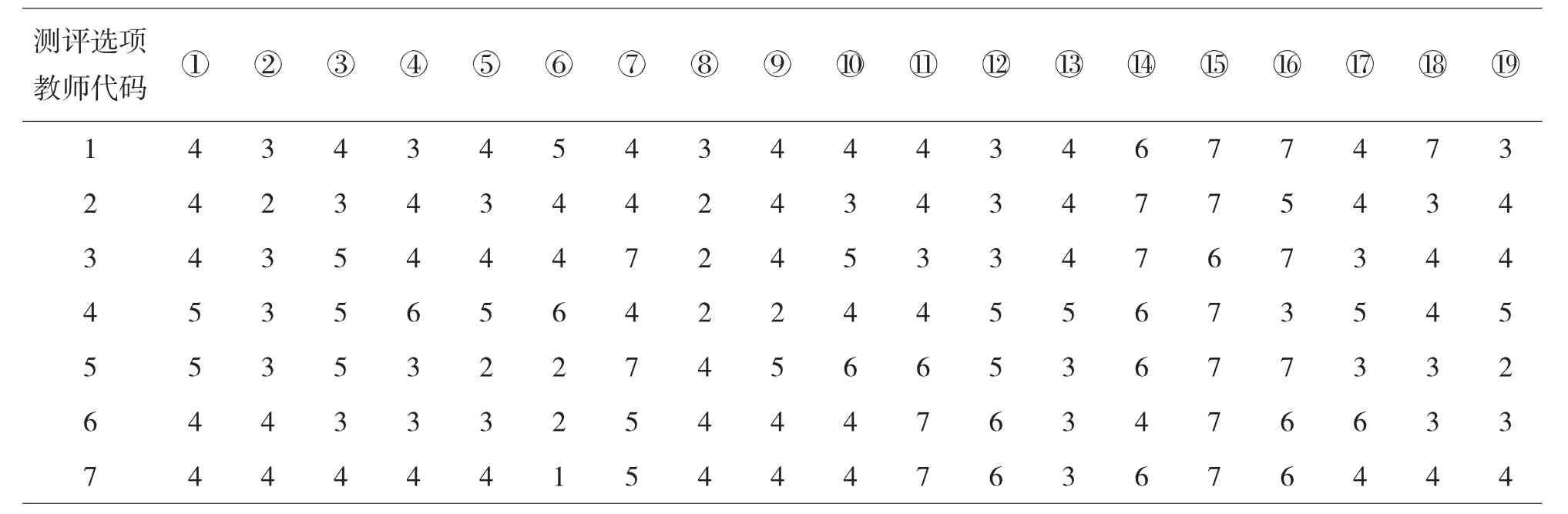
表1 对教师主观评价的众数分析结果

其次，依据以上的打分表，根据灰色聚类分析的算法，可得到聚类白化矩阵xij，其中i=7,j=19.利用matlab7.0进行计算，可以得到白化权系数矩阵为

从上式可以得到：课堂教学质量主观评价为优秀的教师代码是：3，4，6；课堂教学质量主观评价为良好的教师代码是：1，7；课堂教学质量主观评价为不合格的教师代码是2，5.

运用灰色聚类分析方法，可降低课堂教学评价问题中打分的主观性，较好地实现了量化评价与主观评价的结合，从而为公正客观地反映教师课堂教学情况探寻了一条出路.

〔1〕邓聚龙.灰理论基础[M].武昌:华中科技大学出版社，2002.10-13

〔2〕罗党.灰色决策问题分析方法[M].郑州:黄河水利出版社，2005.30-34.

〔3〕胡双喜.大学教师评价体系研究[J].陕西青年职业学院学报，2013（3）：18-20.

〔4〕张千，时念云，张琼声.基础模糊聚类分析的教师评价模型[J].计算机系统应用，2012（12）：168-172.

〔5〕鲁立娜，任参军，徐军，等.睡衣舒适性能主观评价的灰色聚类分析[J].西安工程大学学报，2010（2）：176-179.

〔6〕范辉君、刘庆广，教学质量视角下高职教师评价体系研究[J].南通航运职业技术学院学报2013（1）：（95-99）.

G642

A

1673-260X（2015）12-0015-02