非线性系统的奇异最优控制问题

刘锁铭 王秀红

(鲁东大学数学与统计科学学院,山东烟台 264001)

非线性系统的奇异最优控制问题

刘锁铭 王秀红

(鲁东大学数学与统计科学学院,山东烟台 264001)

讨论非线性系统关于奇异二次型性能指标最优控制问题的近似方法。基于李代数生成向量矩阵的方法,将非线性系统变换为线性非奇异系统,进而利用参数摄动方法通过求解非奇异二次指标最优控制问题的解得到原系统的最优控制律。

李代数法摄动法最优控制奇异二次指标最优控制

最优控制理论对于与控制系统提供了解决的多类现代方法，因此它在线性控制理论中扮演着重要的角色例如，线性二次调节器和现行二次型高斯控制理论。利用最优控制的一类线性系统可以大幅度减少最优控制率的计算幅度。此外，它构成了一个解决非线性最优控制问题的有效方法，其中，李代数法已经被应用于获取非线性偏微分方程的最优反馈率。此外，它构成了一个有效解决非线性最优控制问题的方法。应用这种方法可以计算最优飞船了角动量，以及可以计算太空交通工具最小的燃料消耗。李代数法已成为最优控制理论的一个重要的数学工具[1]。

1 问题描述

考虑一类非线性系统:

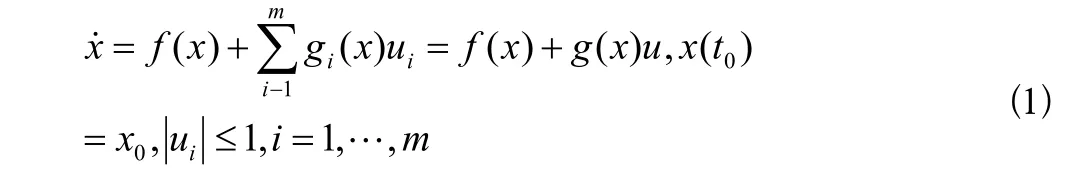
这里x∈Rn，ui为标量，其中i=1,…,m

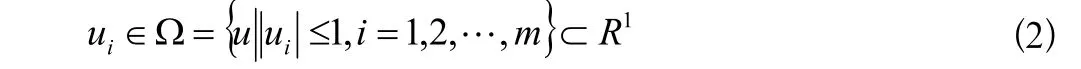
性能指标为:

t0和tf给定，Q为n×n维正定对称矩，系统的矢量场f，gi，Φ(x(tf))平滑。

我们的问题是找到满足条件(1)和(2)的u*使得性能指标J(u)最小。

众所周知，我们缺乏进一步的假设，这类问题通常通过最优控制中的邦-邦控制来解决。

通过非线性系统(1)我们可以定义李代数，从而生成向量场。

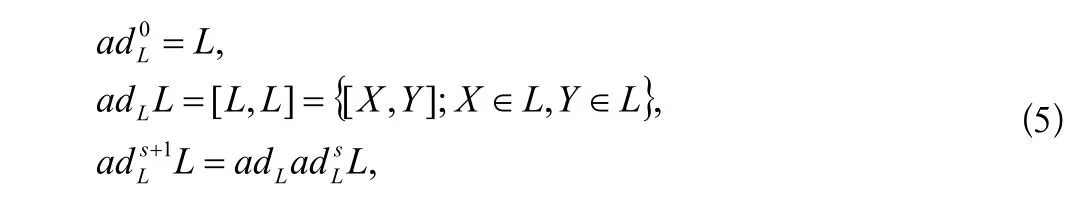
即L是f的集合，这里我们可以定义:

这里我们定义Y][X,为

系统(1)的复杂结构通过构建L代数的方法可以解决此类最优控制问题。解决此类困难的第一步是寻找一类简单系统来近似替代系统(1)。Bressn和Hermes指出，在某些非限定条件下，一种系统仿射的形成，都可以通过构造一个零阶的局部近似的状态方程与之相同。

2 最优控制问题

为了解决第二节中的奇异控制问题，我们给(3)式中添加了一项kε

极小化了这个非奇异的泛函部分，对于εk当k→∞时limk→∞εk=0可以求出(3)式的最优值。此时我们定义

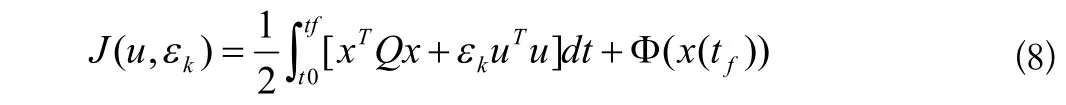
εk≥0此时很明显我们将最优控制问题(1)转化成为非奇异控制问题，通过极小值原理我们可以找到它的Hamiltonian函数:

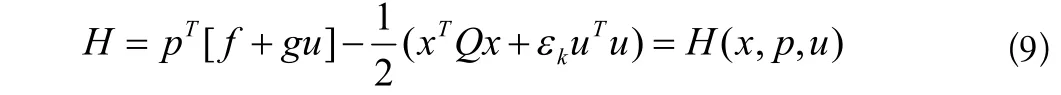
上式中p∈Rn是n×1维的伴随矩阵。

对于(9)式的Hamiltonian 函数，我们可以得到

将1×m维输出矩阵加入(10)式中我们可以得到

对于最优控制问题(1)，(8)式是非退化的

根据最优控制的必要条件我们可以得到

通过(13)式我们可以很明确的得到

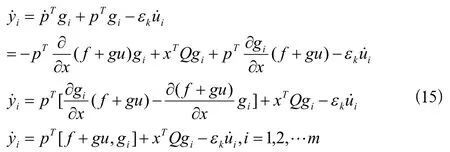
我们也可以求得iy的一阶导数为

并且

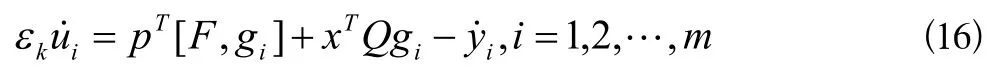
这里

由于

那么(16)式可以变为

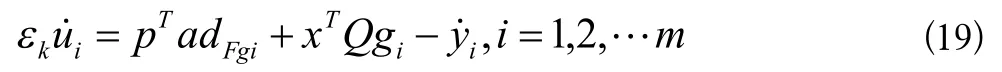
以下是引理及其证明

引理1.令Y为一组向量并令p为它的伴随向量。则

这里F在(17)式中被定义，并且我们可以沿着系统的轨迹来计算时间导数。

证明.:函数YpT沿着系统轨迹的时间导数是

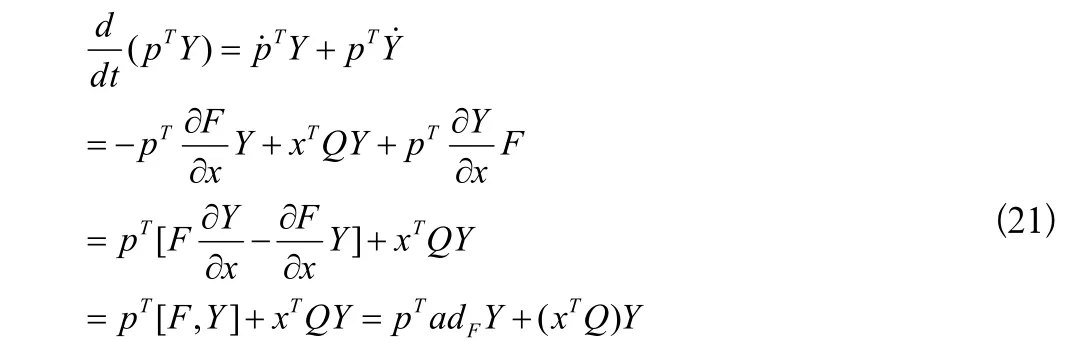
通过引理，我们可以得到(19)式中iu可以进行二阶求导

总之对于任意i=1,2,…,m 均有

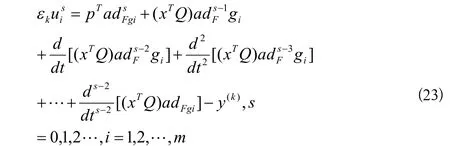
令

表示最优哈密顿函数，则我们将(11)式中),(pxH*替换

后成为最优哈密顿函数。

3 解题方法及步骤

为了解决第三节问题(6)的最优控制问题我们采取的步骤:

步骤1:选取一个初始值ε1≥0和一个控制函数。

步骤2:解决εk-问题(k初始值为1)，并产生一个极小的控制函数。

步骤3:令εk+1≤εk(例如εk+1=εk/10).设

回到步骤2。

当通过步骤2得到δε≺k(δ为无穷小量)时停止运算，否则重复上述步骤。我们可以通过证明以下两种假设来证明我们的方法正确。

假设1:定义(2)式中的Ω为一集合，iu为一标量控制(i=1,2,…,m )且。则，那么通过极小控制uk的到的性能指标J(u,εk)同样属于Ω。

引理2:对于k≥ℓ(εk≤εℓ)我们得到

这里u∈Ω且J0∈R1

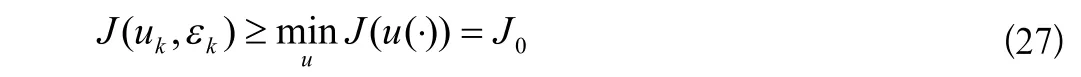
也就是说),(kkuJε对于kε是逐渐递减的。我们也可得出

证明:我们知道

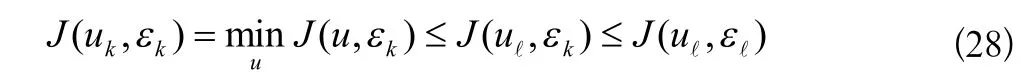
另外，

证明:通过引理2，),(kkuJε是逐渐递减的且有下确界(0J)，那么它一定会聚集于一点。

假设

这里u0被定义为

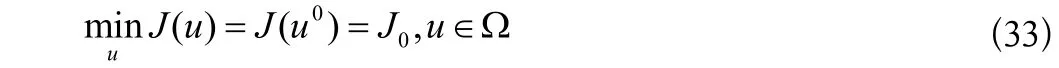
与(31)冲突，则意味着

但是，这意味着既然它单调递减，则

因此，我们得到矛盾并且(30)式一定正确。

然而，我们必须承认这是一个通过使kε无穷小从而逼近近似解得好方法，但是我们仍旧无法从确定它的精确数值。

4 结语

我们考虑了一类非线性奇异最优控制系统。我们通过加入无穷小量εk来使奇异最优控制转化成为非奇异最优控制。其中(25)式中构建最优控制方程u*成为最重要的步骤。它在解决开环最优控制u*(t )的问题上起到了至关重要的作用。

[1]胡寿松,胡维礼.最优控制理论与系统[M].北京:科学出版社,2005.

[2]冯德兴.奇异最优控制的渐进分析.自动化学报第20卷第5期,1994年9月.

[3]杜振华,石明江,田芳.线性系统的奇异最优控制方法研究.制造业自动化(610500).

[4]Daim-Yuang Sun,The solution of singular optimal control problems using the modified line-up competition algorithm with region-relaxing strategy,ISA Transactions 49(2010)106-1113.

[5]MARK ARDEMA Nolinear Singularly Perturbed Optimal Control Problem with Singular Arcs,Automatic.Vol.16,pp.99-104.

[6]Ton Geerts,All Optimal Controls for the Singular Linear-Quadratic Problem Without Stability,Elsebier Science Publishing Co,Inc,1989.

[7]R.E.奥马利《.奇异摄动引论》.科学出版社,1993.