基于拉格朗日方程的积油转子系统力学建模和数值仿真*

许 涛，王美令，张兆丰，韩清凯

（大连理工大学机械工程学院，辽宁大连 116024）

基于拉格朗日方程的积油转子系统力学建模和数值仿真*

许 涛，王美令，张兆丰，韩清凯

（大连理工大学机械工程学院，辽宁大连 116024）

提出一种基于双支撑转子系统的力学简化模型，分析了含有旋转腔体积油故障的转子系统动力学特性。首先，将转子腔体中积油简化为集中质量油团，采用拉格朗日方程，建立了该系统的动力学方程，基于方程解析，分析了不同转速下系统的位移频率响应变化。结果表明，积油转子在旋转过程中，当转速超过系统临界转速时，会出现共振锁频现象。

积油转子；拉格朗日方程；数值仿真

0 引言

旋转机械作为国家航空、动力、化工、能源领域中重要的机械装置，在国民经济和国家安全方面，都占有极其重要的作用，大部分的旋转机械如汽轮机、压缩机、航空发动机等装置内部均有腔体盘鼓结构，由于装置不合理的密封措施或者轴承安装等装配上的问题，常常导致腔体进油或者润滑油泄漏，流入腔体的积油所导致的装置运行故障时有发生[1-3]，而由实验观察到，即使微量的腔体积油，也会对腔体的运转产生极大的影响。带有微量积油的腔体可以称之为含液转子系统，即在旋转部件空腔内积存有微量液体的转子系统，若腔体内进入一定量的液体，则旋转的液体与转子之间的相互作用会使得转子在一定的转速范围内出现运动失稳，即积油自身出现严重的自激振动[4]。

自从Wolf[5]在1968年首次提出积油转子存在自激不稳定区域后，国内外众多学者对积液转子开展了试验和理论方面探索研究工作。Hendricks[6]，Holm[7]，Jorgense[8]分别报道了悬臂、对称支撑、弹性支撑条件下带有部分充液的刚性转子系统的稳定性和涡动性，Yoshizumi[9]建立了忽略转子不平衡、重力和陀螺效应的弹支充液转子系统的耦合动力学模型。国内复旦大学的张文和陶明德[10]基于梁模型和流体二维流动模型，推导了充液转子的摄动方程，得到了充液转子失稳判别的解析表达式，浙江大学的祝长生[11-12]对部分充液的柔性转子，刚性转子系统振动和稳定性进行了较为全面的研究，从实验和理论方面分析了充液转子系统不稳定产生的过程，失稳过程中系统的动力特性以及流体粘度、充液两对转子系统振动和稳定性的影响。

本文针对含有旋转腔体积油故障的转子系统，提出一种双支撑转子系统力学简化模型，将积油简化为集中质量油团，通过拉格朗日方程，建立系统动力学方程。由数值仿真，分析了积油转子系统中转速对积油系统振动响应的影响，以及积油转子系统的共振锁频现象。

1 积油转子系统的力学建模

1.1 动力学模型建立

将少量漏入的积液转换为集中质量油团建立的四自由度转子系统力学模型如图1所示，刚性轴左右各有两个弹性支撑轴承，轴和圆盘一起旋转带动圆盘中简化的油团一起运动，图1中黑色球体表示简化的油团。不考虑轴的质量，设圆盘质量为M，油团质量为m，转子两端由轴承B1和B2支撑，并将支撑轴承简化为水平竖直刚度形式，如图1中的K1X，K1Y，K2X，K1Y所示，油团旋转过程中的位移由Cξηz*坐标系内的轴向位移zB和角位移α共同决定，设定转子系统转速为Ω。系统基本结构参数如表1所示。

图1 积油转子系统力学模型

表1 系统基本结构参数

在该模型中引入地面固定坐标系OXYZ和旋转坐标系Cξηz*，其中OXYZ坐标系中O为坐标原点，Z轴为转子系统的旋转轴线，即左右两支撑轴承的初始中心线，该坐标系固定于地面，坐标系Cξηz*为随转子旋转的旋转坐标系，其中C为转子系统的几何中心。设定运转过程中不存在轴向位移，当系统转速Ω=0时，默认C点和O点重合，则C点在OXYZ坐标系的位移向量

1.2 坐标系建立

由于转子系统旋转过程中复杂的变形形式，不仅需要考虑到其旋转过程中的平动位移，还应考虑整个装置在运行过程中的转动位移，为了准确刻画其运动形式，引入以下坐标系，如图2所示。

图2 力学模型多维坐标系

（1）依据转子几何中心C点建立坐标系CX′Y′Z′，该坐标系在系统转速为0时和坐标系OXYZ重合，在旋转过程中和坐标系OXYZ各坐标轴平行。

（2）设定转子系统在CX′Y′Z′坐标系内沿X′轴角度位移大小为φX′，原坐标系沿X′轴旋转角度 φX′得到CX′yz坐标系，两坐标系转化向量为R1。

（3）设定转子系统在CX′yz坐标系内沿y轴角度位移大小为φy，原坐标系沿y轴旋转角度φy得到Cxyz∗坐标系，两坐标系转化向量为R2。

（4）由于该转子系统为定转速旋转，设定旋转坐标系Cξηz∗，该坐标系为固定坐标系Cxyz∗旋转角度θ得到，其中θ=Ωt，其值随着系统旋转而增大。

已知C点为转子系统的几何中心，G点为转子系统的质心，由于系统会不可避免存在制造误差和不平衡受力，几何中心和质心往往不重合，故设C点和G点在Cξηz∗坐标系内距离偏差为ε，角度偏差为β，同时，由于偏心的原因，转子的极惯性轴和Cξηz∗坐标系的η轴也存在一定的角度偏差，设该角度为 χ，旋转得到Gp1p2p3极惯性矩坐标系，如图3所示。

图3 极惯性矩坐标系

表2 坐标系转换及其转换向量

表2中R1，R2，R3，R4转换矩阵表达式如下

1.3 基于拉格朗日能量求解的动力学方程

本积油转子系统力学模型中，不考虑广义力项，则系统的拉格朗日方程为如下形式：

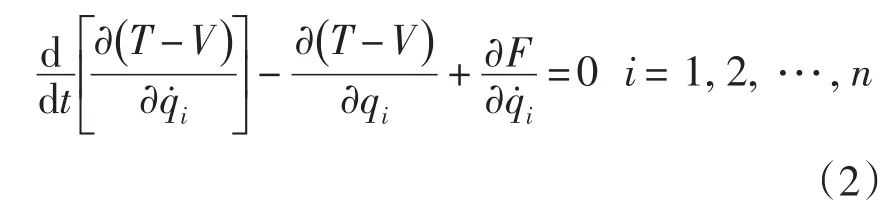
其中，方程广义坐标向量qi为：

系统动能为：

其中，r˙G-O为转子质心的速度向量；r˙B-O为油团的速度向量；Ωp表示的为转子角速度向量转换到极惯性矩坐标系内的角速度向量；J表示的为转盘的转动惯量矩阵。

系统势能求解公式如下[14]：

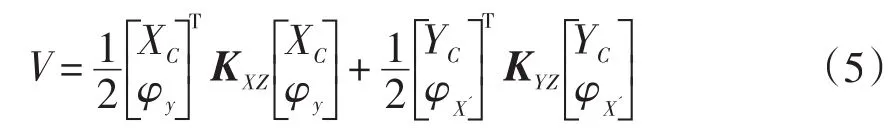
其中，KXZ，KYZ分别表示的是系统在XZ平面的刚度矩阵和在YZ平面的刚度矩阵。

设油团在圆盘轨道内的运动阻尼为cB，考虑瑞利阻尼函数，则表达式中阻尼能量为

考虑系统整体阻尼因素的存在，将系统阻尼考虑为瑞利阻尼，即比例阻尼，其求解公式如下

λ和η可由如下公式求得[13]：

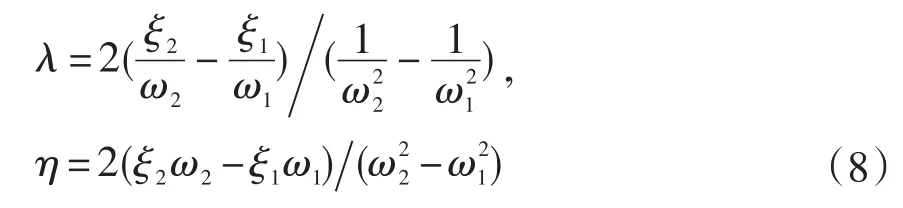
其中，ξ1, ξ2为阻尼系数，ω1, ω2为转子的一、二阶临界转速。

将方程（4），（5），（6）带入方程（2）中，并加入系统整体阻尼，得到该积油转子系统的四自由度动力学方程和耦合方程

由方程（9）可得系统的质量矩阵和刚度矩形式如下

2 积油转子系统的数值仿真分析

基于系统动力学方程，利用Runge-Kutta数值法对该二阶多元微分方程进行求解，通过Matlab数值仿真，采用时域、频域、三维谱图曲线分析了积油转子系统在不同转速下的响应形式[15]。

已知积油系统一阶固有频率为33.4 Hz，设置仿真参数中积油质量为1.85 g，体积为2 ml，仿真测点为系统的几何中心C点，设置仿真分析条件如下：采样频率为750 Hz，FFT分析取总采样数据点的后数据量，三维谱图取每组800个数据点作为一组进行分析。

（1）转速Ω=10 Hz

仿真测点振动响应分析的时域图如图4(a)所示，频域图如图4(b)所示。

图4 转速为10 Hz时系统振动响应

由图4可看出，仿真测点的时频曲线达到稳定值，频谱图只出现了单一的工频，没有倍频成分。

（2）转速Ω=20 Hz

仿真测点振动响应分析的时域图如图5(a)所示，频域图如图5(b)所示。

由图5可以看出当系统转速上升到20 Hz后，系统的时域波形出现了波形叠加，整体振幅略高与转速为10 Hz时的振幅，同时，系统出现了多阶频率，各频率成分的幅值变化较大，但频率成分仍以工频成分占主导。

（3）转速Ω=40 Hz

仿真测点振动响应分析的时域图如图6(a)所示，频域图如图6(b)所示。

图6中，系统的时域波形呈周期性变化趋势，波形叠加较明显，最大幅值较图4、图5成倍上升，值得注意的特征是，虽然系统转速已经越过临界转速，但是系统临界转速时激起的共振仍然在系统振动中占主导成分，同时，由于此时转速接近临界转速，振动幅值仍大于10 Hz、20 Hz时测点最大振幅。

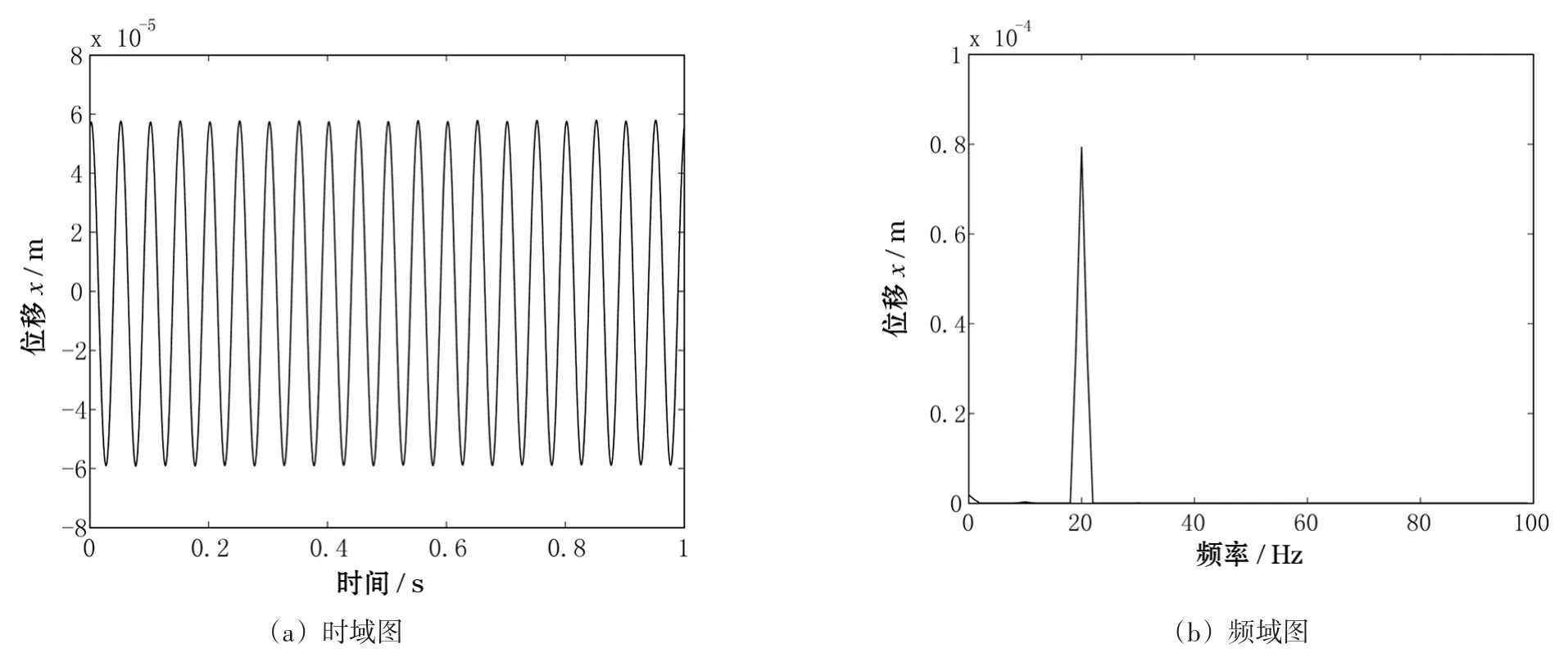
图5 转速为20 Hz时系统振动响应

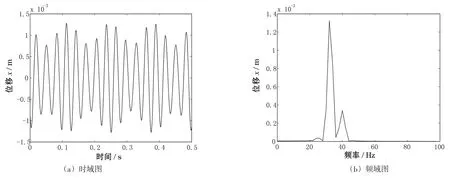
图6 转速为40 Hz时系统振动响应

（4）转速Ω=60 Hz

仿真测点振动响应分析的时域图如图7(a)所示，频域图如图7(b)所示。

由图7可以看出，当系统转速上升到60 Hz时，系统时域波形仍然为叠加波形，波形平均幅值较40 Hz时下降较多，但仍高于低转速时的系统振幅，频谱图中仍有多种频率成分存在，其中临界转速仍占主导成分，由临界转速激发的共振幅值较40 Hz时也出现下降趋势，但高于由系统工频激发的振动幅值。

（5）位移频率三维谱图

考虑以上过临界转速后，系统频谱中始终存在的临界成分，为了从更大范围研究此临界成分，对该转子系统由5 Hz到75 Hz绘制了位移频率三维谱图，如图8所示。

由图8积油转子系统x轴方向的三维谱图可以看出，当系统转速低于临界转速时，系统以工频振动为主导成分，振动幅值较小，到达临界转速时系统振动幅值达到最大，之后系统的工频振动恢复到较低幅值，但系统的临界共振并没有随着转速的改变而消失，而是在临界转速处长时间维持在高振幅状态，此种振动形式即为积油转子系统的共振锁频现象。

3 结论

本文以旋转机械中常见的积油故障为主要研究对象，通过模型简化建立了积油转子系统动力学模型，并由数值仿真，分析研究了转速对积油转子系统振动响应的影响。仿真结果表明，积油转子系统在不同转速下的响应变化较为复杂，在转速低于系统临界转速时，系统的振动以工频振动为主，当转速超过系统临界转速后，系统表现出独特的共振锁频现象，最大振幅始终维持在临界转速处，并伴有一定幅值的工频振动。本结论验证了文献[4]中的实验和分析结果，并为转子系统积油故障的辨识和处理提供了一定的理论支撑。

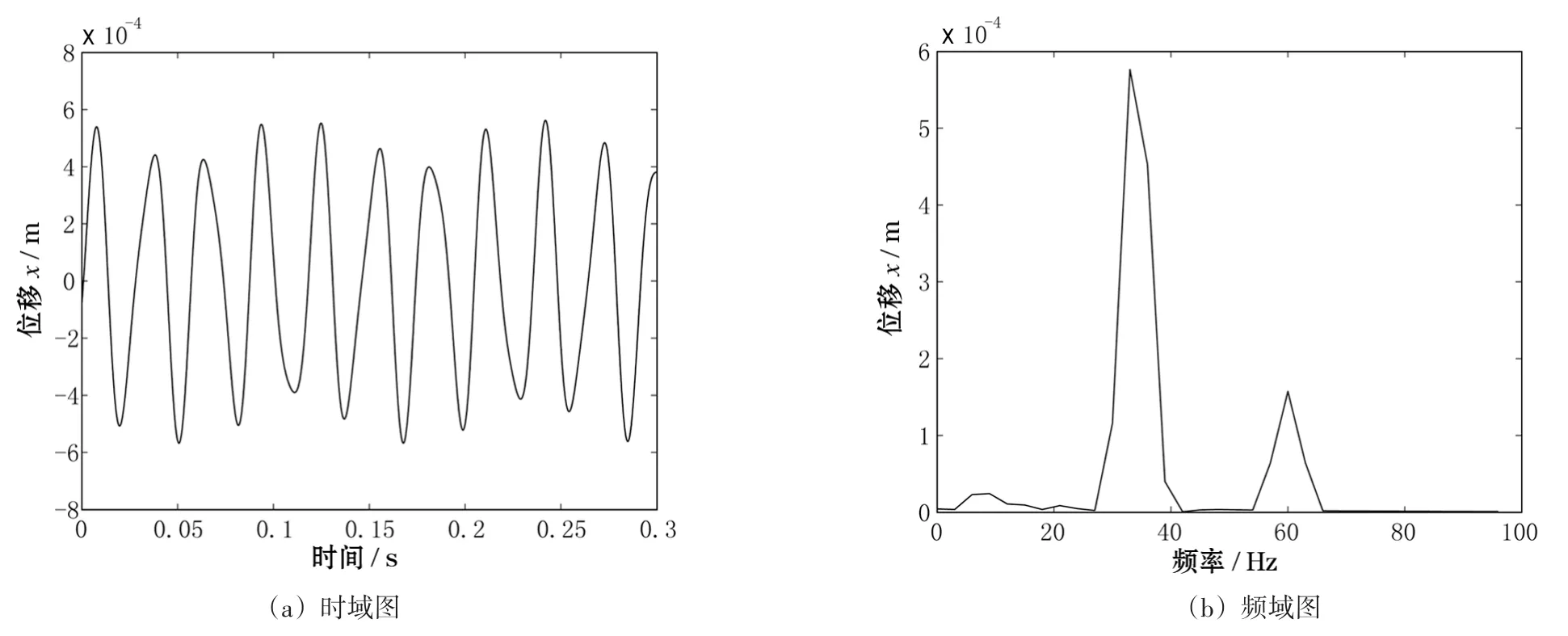
图7 转速为60 Hz时系统振动响应

图8 积油转子系统x轴方向三维谱图

［1］罗剑斌，卢一兵，袁立平，等.汽轮机转子中心孔进油引起的振动分析［J］.电力安全技术，2005（7）：6-7.

［2］张其显，刘晓锋.汽轮机转子中心孔进油诱发异常振动故障分析诊断［J］.汽轮机技术，2007，49（1）：57-59.

［3］姜广义，武鹏，张洁.航空发动机腔内积油引发振动故障分析［J］.航空发动机，2013，39（2）：75-78.

［4］Q.Han，M.Wang，H.Chu.Nonsynchronous Vibrations of Rotor System with an Oil-Block inside the Rotating Drum［J］.Advances in Vibration Engineering，2013，12（2）：165-178.

［5］Wolf J A.Whirl Dynamics of a Rotor Partially Filled With Liquid［J］.Journal of Applied Mechanics，1968，35（4）：676-682.

［6］Hendricks S L.Stability of a Clamped-Free Rotor Partial⁃ly Filled With Liquid［J］.Journal of Applied Mechan⁃ics，1986，53（1）：166-172.

［7］Holm christensen O，Trager K.A Note on Rotor Instabili⁃ty Caused By Liquid Motions［J］.Journal of Applied Mechanics，1991，58（3）：804-811.

［8］Coldingjorgensen J.Rotor Whirl Measurements on a Long Rotating Cylinder Partially Filled With Liquid［J］.Jour⁃nal of Vibration and Acoustics， 1993， 115（2）：141-144.

［9］Yoshizumi F.Self-Excited Vibration Analysis of a Rotat⁃ing Cylinder Partially Filled with Liquid［J］.Journal of System Design and Dynamics，2011，5（2）：372-387.

［10］Tao M，Zhang W.Dynamic stability of a flexible spin⁃ning cylinder partially filled with liquid［J］.Journal of Applied Mechanics，2002，69（5）：708-710.

［11］祝长生.部分充液悬臂柔性转子系统不稳定特性的实验研究［J］.振动工程学报，2004，（04）：65-68.

［12］Zhu C S.Experimental Investigation Into the Effect of Fluid Viscosity on Instability of an Over-hung Flexible Rotor Partially Filled With Fluid［J］.Journal of Vibra⁃tion and Acoustics，2006，128（3）：392.

［13］韩清凯，于涛，王德友.故障转子系统的非线性振动分析与诊断方法［M］.北京：科学出版社，2010.

［14］ Genta G.Dynamics of rotating systems［M］.New York：Springer，2005.

［15］毛丁辉，邱建琪，史涔溦.基于SVPWM的电动汽车直接转矩控制方法研究［J］.机电工程，2014（07）：830-835.

Mechanical Modeling and Numerical Simulation of Oil Leakage Rotor System Based on the Lagrange Equation

XU Tao，WANG Mei-ling，ZHANG Zhao-feng，HAN Qing-kai
（School of Mechanical Engineering，Dalian University of Technology，Dalian 116024，China）

On account of the operation faults caused by the oil leakage in rotor cavity，to explore its dynamic characteristics，a double-support simplified rotor model has been proposed.In the model，leak oil is transformed into a concentrated mass oil-block.Then the dynamic equation is deduced by the Lagrange equation，based on the numerical simulation，vibration responses caused by the rotating speed are investigated.Result shows that frequency-locking phenomenon will appear when the rotating speed exceeds the first critical speed.

oil leakage rotor；Lagrange equation；numerical simulation

TH123

A

1009－9492(2015)10－0055－06

10.3969/j.issn.1009-9492.2015.10.014

许 涛，男，1989年生，河南信阳人，硕士研究生。研究领域：转子动力学，故障诊断。

(编辑：向 飞)

*国家重点基础研究发展计划（973计划）资助项目（编号：2012CB026000）；国家自然科学基金资助项目（编号：51175070）

2015－05－28