基于随机网络演算的无线通信系统能耗分析*
李鹏翔,李职杜,高月红,张欣
(北京邮电大学,北京 100876)
基于随机网络演算的无线通信系统能耗分析*
李鹏翔,李职杜,高月红,张欣
(北京邮电大学,北京 100876)
提出了一个在一定传输时延约束下能量消耗最少的最优化问题,并建立了相应的无线通信系统模型,然后利用随机网络演算理论研究时延约束、传输速率与能量消耗之间的关系,最后得出了最优化问题的最优解。
时延约束;传输速率;能量消耗;随机网络演算
近几年,随着绿色通信成为热点话题,通信运营商越来越关注全方位的绿色环保和节能减排。由于无线通信系统主要依靠消耗不可再生资源产生的能量来维持工作,因此减少能量消耗对于保护自然资源和改善生活环境都至关重要。许多最新研究都致力于减少能量消耗和提高资源利用率。例如,在一定通信时延约束下延长移动终端电池寿命的方案[1]。在高速网络领域,经常需要定性或定量分析网络负载变化对整个网络的影响,而传统数学工具如概率论、排队论等方法在扩展性和精确度方面存在一些不足之处。网络演算就是在这种情况下被开创和发展的一种新兴理论[2~6]。随机网络演算的核心思想是通过到达曲线和服务曲线的特性来分析积压界限和时延约束界限的概率分布,它通常给出一个概率性的界限而不是确定的数值,并且通过这个概率性界限去处理随机性问题。因此,随机网络演算适用于充满随机性的无线通信系统。
1 系统模型
考虑只包含一个数据源和一个信道无线通信系统模型。假设时间是离散的,初始时刻系统内无数据分组残存。数据分组到达信道的过程为周期过程,即每隔时间τ有一个大小固定为L的数据分组到达信道。对于信道而言,马尔科夫on-off信道模型下的传输时延与Gilbert-Eliott on-off信道模型下的系统性能已有详细的论证[7,8],这说明讨论一般on-off信道模型的价值性与必要性。本文将信道定义为一种无记忆的伯努利on-off信道,即系统在任意单位时间间隔内以概率p提供恒定速率为C的服务,以概率(1-p)不提供服务,并且系统服务是关于时间独立的,实际服务并不会根据已有的服务进行调整。并且,信道传输数据分组需要消耗能量。
数据分组在某些时间段内的到达率可能会大于信道的传输速率,但是不会一直大于信道传输速率,否则将导致数据分组无限积压、系统不稳定。数据分组到达时信道若处于关闭状态,则这些数据分组被寄存在一个容量无限的缓存器中,这样就保证了不会有数据分组丢失,从而保证了系统传输的可靠性。规定信道的传输速率必须大于数据分组的平均到达率,但是一定时间段内系统仍可能有数据分组的积压,本文只分析这一特定时间段内的系统能量消耗。
设数据分组的平均到达率为r(θ),每个时间间隔消耗的能量为E,每个数据分组的实际传输时延为D(t)。传输时延约束用一个概率性的集合(t0, p0)表示,即D(t)大于t0的概率不能超过p0,表示为Pr{D(t)>t0}≤p0。较低的传输速率消耗的能量较少,但会导致一个较大的传输时延。那么,系统的能量消耗,传输速率和传输时延三者之间的关系可以转化为在一定传输时延约束下能量消耗最少的最优化问题,即:
min E(D(t),C); s.t. r(θ)≤C
Pr{D(t)>t0}≤p0
2 随机网络演算的基本特性
网络演算分为确定性网络演算和随机网络演算。确定性网络演算常用于分析系统的最差性能[9],随机网络演算常用语分析动态系统的性能[10,11]。这一部分主要介绍了随机网络演算到达曲线、服务曲线和时延界限的定义与特征以及如何运用它们去解决第二部分中的提到的最优化问题。
用A(t)表示(0,t]时间段内到达信道的总数据分组量, A*(t)表示(0,t]时间段内离开信道的总数据分组量,那么A(t)拥有一个界限函数为f(x)的随机到达曲线α(t),表示为A(t)~SAC<α(t), f(x)>,对任意的t≥s≥0和x≥0,表示为:
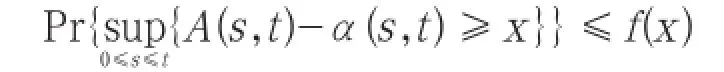
信道提供一个界限函数为g(x)的随机服务曲线β(t),对任意的t≥s≥0和x≥0,表示为:

假设一个系统的到达过程A(t)拥有一个界限函数为f(x)的随机到达曲线α(t),并且系统提供的服务过程拥有一个界限函数为g(x)的随机服务曲线β(t),则对任意的t≥0和x≥0,有:
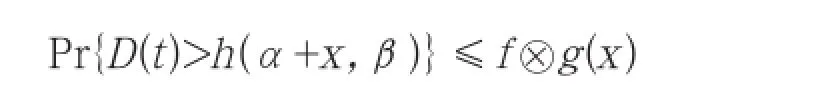
其中h(α+x,β)表示函数(α(t)+x)和β(t)之间的最大水平距离,定义为:

3 能耗分析
3.1 传输速率与时延约束的关系
在建立的系统模型中,数据分组的到达过程为周期过程。根据随机网络演算的性质,可以得到界限函数f (x)与随机到达曲线α(t)分别为:
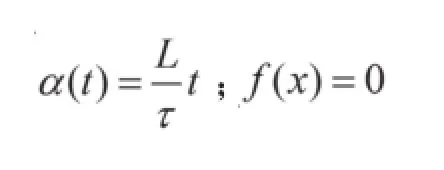
那么数据分组平均到达率的上界r(θ)为:
r(θ)=L/τ
对于无记忆的伯努利on-off信道,根据随机网络演算的性质,可以得到界限函数g (x)与随机服务曲线β(t)分别为:
其中p表示信道服务概率。信道的平均服务速率为:
其中θ是一个自由变量。根据随机网络演算的性质,延迟参量h(α+x,β)为:
所以传输时延约束的概率分布函数为:
综上,则有以下式子成立:
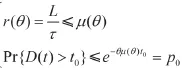
由上式,θ被一个不等式限制,同时又满足一个关于θ的恒等式。这样就可以得出在一定传输时延约束和数据分组平均到达率约束下的最小传输速率Cmin,表示为:
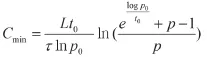
3.2 最小能量消耗
在上一部分中,最小传输速率和时延约束之间的关系已经得出。根据香农公式,最小传输速率Cmin还与能量消耗有关系,表示为:

其中W表示信道的带宽,N0表示噪声功率谱密度,P表示传输功率。则传输功率P可以表示为:
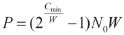
至此,在一定传输时延约束和数据分组平均到达率约束下的最小能量消耗闭式解已经得出,表示为:
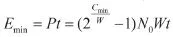
其中t表示平均传输时间,为:
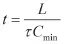
4 数值分析及仿真结果
4.1 信道服务概率、概率性时延约束与时延约束的关系
概率性时延约束p0、信道服务概率p与时延约束t0这3个参数并不可以任意赋值,三者之间的约束关系为:
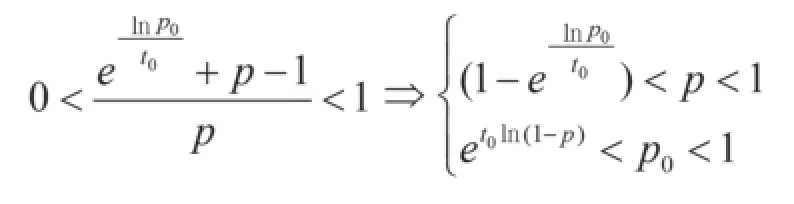
首先讨论信道服务概率p与时延约束t0的关系,信道服务概率p的最大值为1,令概率性时延约束p0=0.1,则得到图1所示结果。
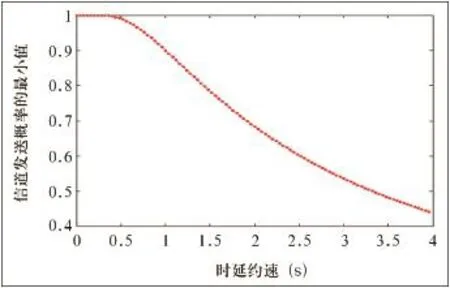
图1 信道服务概率的最小值与时延约束的关系
由图1可知,在概率性时延约束确定的情况下,信道服务概率的最小值是随着时延约束的增加而减小的。当时延约束为一个给定值时,其对应的纵坐标的值为信道服务概率可取的最小值,这样才能保证最小传输速率有意义。当时延约束为一个给定范围时,范围起始值对应的纵坐标的值为信道服务概率可取的最小值。在接下来的讨论中,信道服务概率和时延约束的取值必须符合上述约束条件。
然后讨论概率性时延约束p0与时延约束t0的关系,概率性时延约束t0的最大值为1,令信道的服务概率p=0.99,则得到图2所示结果。具体分析过程与图1的分析过程类似,这里不再赘述。
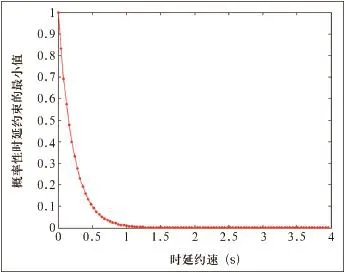
图2 概率性时延约束的最小值与时延约束的关系
4.2 最小能量消耗与时延约束的关系
下面讨论最小能量消耗与时延约束的关系。令噪声功率谱密度N0=10-7W/Hz,信道带宽为W=11 MHz,固定的数据分组大小L=1 Mbit/s,数据分组达到时间间隔τ=0.1 s。结合图1和图2,选取时延约束为[0.7 s, 4 s], 信道服务概率p=0.99,概率性时延约束p0=0.1[12]。如图3所示,每一个时延约束都对应着唯一的最小能量消耗,这表示在一个确定的时延约束下的最优化问题有唯一解。另外,最小能量消耗随着时延约束的增加而减少,这是因为时延约束的增加将导致最小传输速率的减少,使最小能量消耗减少。
当时延约束t0趋于无穷大的时候,根据洛必达法则对最小传输速率Cmin进行化简,得到:
Cmin= L/τp
所以信道的最小传输速率不小于数据分组的平均到达率。在仿真中,当时延约束足够大的时候(图3中的时延约束 ),信道的最小传输速率将趋向于数据分组的平均到达率,使最小能量消耗趋近于一个固定值。
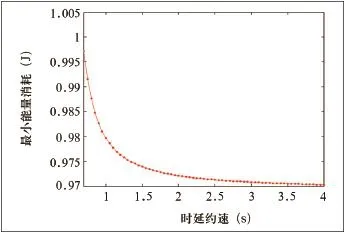
图3 最小能量消耗与时延约束的关系
4.3 最小能量消耗与信道服务概率的关系
现在讨论信道服务概率p对最小能量消耗Emin的影响。令噪声功率谱密度N0=10-7W/Hz,信道带宽为W=11 MHz,固定的数据分组大小L=1 Mbit/ s,数据分组达到时间间隔τ=0.1 s,概率性时延约束p0=0.1 s。结合图1,选取时延约束为[0.7 s, 2 s],信道服务概率分别为:p0=0.97、p0=0.98、p0=0.99。3种情况下最小能量消耗与时延约束的关系如图4所示。
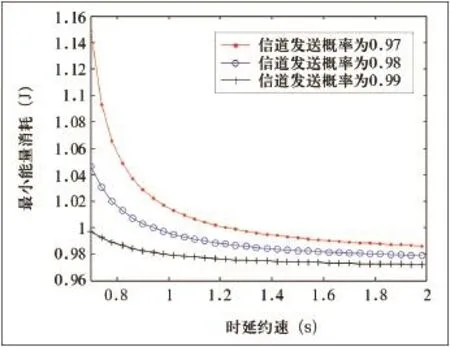
图4 最小能量消耗与时延约束的关系
由图4可知,在相同的时延约束下最小能量消耗随着信道服务概率的增加而减少。这是因为随着信道服务概率的增加,最小传输速率减少,导致最小能量消耗的减少,也可以定性分析这一变化趋势,若信道要在一段时间内传输一定量的数据分组,随着信道服务概率的增加,信道的最小传输速率可以相应减少,从而使最小能量消耗越少。在仿真中,当时延约束足够大的时候(图4中的时延约束t0=2 s),最小能量消耗将趋向稳定,但是由于信道服务概率不同,导致最小传输速率略有不同,因此最小能量消耗会有细微差异。
4.4 最小能量消耗与概率性时延约束的关系
现在讨论概率性时延约束p0对最小能量消耗Emin的影响。令噪声功率谱密度N0=10-7W/Hz,信道带宽为W=11 MHz,固定的数据分组大小L=1 Mbit/s,数据分组达到时间间隔τ=0.1 s,信道服务概率p=0.99。结合图2,选取时延约束为[0.7 s, 4 s],概率性时延约束分别为:p0=0.1、p0=0.2、p0=0.3。3种情况下最小能量消耗与时延约束的关系如图5所示。
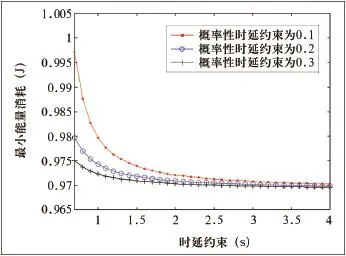
图5 最小能量消耗与时延约束的关系
由图5可知,在相同的时延约束下最小能量消耗随着概率性时延约束的增加而减少。这是因为概率性时延约束p0表示所能忍受的超过时延约束的概率,p0越大,意味着所能忍受的概率越大,即服务质量要求越低,因此数据分组可以以一个相对比较低的速率传输,使最小能量消耗减少。在仿真中,当时延约束足够大的时候(图5中的时延约束t0=4 s),最小能量消耗将趋向稳定,虽然概率性时延约束的不同,但是最小传输速率的近似解与其无关,故3种情况下最小能量消耗相同。
5 结束语
本文应用随机网络演算理论完成了对无线通信系统模型的能耗分析,得到了时延约束、传输速率与能量消耗的关系,并且研究了传输过程中不同的因素对能量消耗的影响,完成了定性与定量的分析,得到了比较可靠的结果,为减少无线通信系统中的能量消耗提供了理论依据。
[1] Gao Y, Jiang Y. Analysis on the battery lifespan of a mobile terminal under probabilistic delay constraint[C]//Proceedings of the 3rd International Conference on Future Energy Systems: Where Energy,Computing and Communication Meet. ACM, 2012: 11.
[2] Chang C S. On deterministic traffic regulation and service guarantees: a systematic approach by filtering[J]. Information Theory, IEEE Transactions on, 1998, 44(3): 1097-1110.
[3] Chang C S. Stability, queue length and delay, Part Ⅰ: deterministic queuing networks[R]. IBM Technical Report, RC 17708, 1992.
[4] Cruz R L. A calculus for network delay. I. Network elements in isolation[J]. Information Theory, IEEE Transactions on, 1991, 37(1): 114-131.
[5] Agrawal R, Cruz R L, Okino C, et al. Performance bonds for flow control protocols[J]. IEEE/ACM Transactions on Networking (TON),1999, 7(3): 310-323.
[6] Le Boudec J Y. Application of network calculus to guaranteed service networks[J]. Information Theory, IEEE Transactions on, 1998,44(3): 1087-1096.
[7] Xu T, Chen X, Xiang X, et al. Delay analysis for cognitive radio networks with parallel Markov modulated on-off channels[C]//Wireless and Pervasive Computing (ISWPC), 2012 7th International Symposium on. IEEE, 2012: 1-5.
[8] Gao Y, Jiang L, Jiang Y. Application of stochastic network calculus in cognitive radio network analysis: A case study[C]//Broadband Network and Multimedia Technology (IC-BNMT), 2011 4th IEEE International Conference on. IEEE, 2011: 183-187.
[9] Le B, Jean Y, Patrick T, et al. Network calculus: a theory of deterministic queuing systems for the internet[M]. Heidelberg: Springer,2001.
[10] Jiang Y, Liu Y. Stochastic network calculus[M]. Heidelberg: Springer,2008.
[11] Jiang Y. A note on applying stochastic network calculus[A] .SIGCOMM 2010 [C].Pisa, Italy: ACM Computer Communication Review, 2010. [12] Li Z, Gao Y, Sang L, et al. Analysis on the energy consumption in stochastic wireless networks[C].//Communications Workshops (ICC),2014 IEEE International Conference on.IEEE,2014: 866-870.
Energy consumption analysis for wireless system using stochastic network calculus
LI Peng-xiang, LI Zhi-du, GAO Yue-hong, ZHANG Xin
(Beijing University of Posts and Telecommunications, Beijing 100876, China)
With the objective to minimize energy consumption under a certain transmission delay constraint, a wireless network model is proposed in this work. Then, the theory of stochastic network calculus is used to investigate the relationship among delay constraint transmission rate and energy consumption. In the end, the optimum solution of the optimization problem is achieved.
delay constraint; transmission rate; energy consumption; stochastic network calculus
TN929.5
A
1008-5599(2015)03-0081-05
2014-12-10
国家自然科学基金项目(No.61300185)、北京高等学校青年英才计划项目(YETP0430)。

