Inexactgraph matchingusingahierarchy ofmatching processes

c

○The Author(s)2015.This article is published with open access at Springerlink.com

Paul Morrison1,Ju Jia Zou1()

Inexactgraphmatchingusingahierarchyofmatching processes

c

○The Author(s)2015.This article is published with open access at Springerlink.com

Paul Morrison1,Ju Jia Zou1()

Inexact graph matching algorithms have proved to be useful in many applications,such as characterrecognition,shapeanalysis,andimage analysis.Inexactgraphmatchingis,however, inherentlyanNP-hardproblemwithexponential computationalcomplexity.Muchoftheprevious research has focused on solving this problem using heuristics or estimations.Unfortunately,many of these techniques do not guarantee that an optimal solution will be found.It is the aim of the proposed algorithm to reduce the complexity of the inexact graph matching process,while still producing an optimal solution for a known application.This is achieved by greatly simplifying each individual matching process,and compensating for lost robustness by producing a hierarchy of matching processes.The creation of each matching process in the hierarchy is driven by an application-specific criterion that operates at the subgraph scale.To our knowledge,this problem has never before been approached in this manner.Results show that the proposed algorithm is faster than two existing methods based on graph edit operations. The proposed algorithm produces accurate results in terms of matching graphs,and shows promise for the application of shape matching.The proposed algorithmcaneasilybeextendedtoproducea sub-optimal solution if required.

graph matching;inexact graph matching; graph edit distance;graph edit operations; shape matching

1　Introduction

Graphs have proved to be extremely useful and versatile tools in the areas of image processing, computervision,andpatternrecognition.The versatility of graphs stems from their ability to represent virtually any kind of information in a way that is amenable to various forms of interpretation and manipulation.

Graphmatchingistheprocessofforming correspondences between parts of one graph and parts of another graph.Graph matching has been used in many applications,particularly in the field of visual media processing.They include 2D and 3D image analysis(e.g.,shape recognition),interactive image editing(e.g.,patch-based image synthesis), document processing(e.g.,handwritten character recognition),biometric identification(e.g.,human face recognition),image databases(e.g.,image retrieval),video analysis(e.g.,object tracking), and biomedical applications(e.g.,identification of coronary arteries from medical images)[1-4].A typical problem in shape recognition can be tackled in three steps,namely,the decomposition of a shape into parts,the representation of the parts and their relations using a graph,and the search for correspondence between this graph and that of a known object.In this case,the skeleton of the shape is often used as the graph for shape representation and matching[5].For a typical problem in patchbased image synthesis,an image is divided into regions and then described by a graph where nodes represent the regions and edges represent spatial relations between the regions.The image can then be modified by replacing some of its regions by suitable regions obtained from an image database using contextual graph matching[2].The image canalso be augmented by adding extra regions based on graph matching[4].Interested readers are referred to relevant review papers,e.g.,Refs.[1,3],for other problems in visual media processing which can be posed as graph matching problems.

A graph matching algorithm can generally be placed into one of three broad categories:graph isomorphism,subgraph isomorphism,and inexact graph matching.If the two graphs being matched are not identical,correspondences cannot be formed by a graph isomorphism algorithm.Subgraph isomorphism relaxes this constraint somewhat,and allows matching of one graph with a subgraph of another graph.However,the subgraph must represent the other graph exactly for a match to be made.Occlusion,articulation,and other forms of noise are often present in real-world applications,which only the third form of graph matching,inexact graph matching,is robust enough to resolve.Rather than indicating whether a match exists or not,inexact graph matching outputs some kind of similarity measure in addition to forming correspondences between graph nodes and/or edges. Inexact graph matching is the most useful and commonly-used form of graph matching.Inexact graph matching is the topic of this paper.

Tree search algorithms are commonly used to perform inexact graph matching.In these methods, a tree(state space)is constructed,where each state represents a partial mapping between nodes and/or edges in the two graphs being matched.The goal is to find the state that has the lowest cost, which represents the optimal match between the two graphs.

The first method using tree search techniques was developed by Tsai and Fu[6,7].Here,the concepts of graph edit cost and graph deformation are introduced.To guarantee that an optimal match is always found,a large number of states will often need to be searched.To reduce the number of states searched,Tsai and Fu utilise any available heuristic information to guide the search.For every child state of a given state,they estimate a lower bound on the cost from that child state to a goal state.This information is then used to prioritise the searching of different branches in the tree.

Variousmodificationstothisideawere subsequentlyproposed,inbothbranch-andbound algorithms and look-ahead algorithms such as A*[6,8].Such algorithms have previously been used in artificial intelligence[9].While such estimates using heuristics can drastically reduce the time taken to search the state space,they often do not guarantee that the optimal solution will be found.Other techniques have also been applied to the inexact graph matching problem, such as relaxation labeling[10]and graduated assignment[11].While many of these algorithms do not guarantee that an optimal solution will be found,they are often very fast(they typically run in polynomial-time).We refer readers to Refs.[12-14] for more comprehensive reviews of inexact graph matching algorithms.

OptimalinexactgraphmatchingisanNP-hardproblem,withexpectedexponential-time computational complexity.As in many graph-related tasks of high computational complexity,inexact graph matching algorithms often trade optimality for faster time,and vice versa.Finding an optimal solution may not be critical in many applications. In other applications,however,an optimal solution will be desirable[15].Where optimality is required, many inexact graph matching algorithms will only be of practical use when matching graphs with a few nodes and/or edges.The high computational complexity of current optimal methods poses a significant problem,which we attempt to address in this paper.Indeed,there has been some recent interest in reducing the computational complexity of inherently NP-hard problems,particularly in the field of graph theory[16-20].

We presume that the optimal solution not only depends on the properties of the graphs being matched,but also depends on the application of the graph matching algorithm.This is often implementedbyembeddingapplication-specific attributes in the nodes and edges of the graphs,but this is on a local scale only.A hierarchical matching scheme is proposed,that includes an applicationspecific criterion that operates on the subgraph scale.This scheme allows an optimal match to be found for the given application.The proposed algorithm is based on graph edit operations,but is less computationally intensive than the typical methodbasedongrapheditoperations.The proposed algorithm does not require heuristics orestimations,but rather allows optimizations through the use of more application-specific information.To our knowledge,the problem of high computational complexity in inexact graph matching has never before been approached in this way.

This paper is organised in the following manner. In Section 2,the proposed algorithm is described by building on the existing graph matching theory. Section3presentsacomparisonbetweenthe computational complexities of the proposed method and an existing method that is typical of many previous inexact graph matching algorithms.Results are given in Section 4,and finally,conclusions and opportunities for further research are discussed in Section 5.

2　Hierarchical graph matching

2.1Graphs

A graph is defined by a tuple g=(V,E,α,β)where

·V is the finite set of vertices(nodes),

·E is the finite set of edges,

·α:V→L is the node labeling function,and

·β:E→L is the edge labeling function.

L is a finite alphabet of labels for nodes and edges. Labels,or attributes,are values derived from the application-specific information on which the graph is based.Assigning labels to nodes and edges,using α and β,respectively,adds semantic information to the graph representation.Edges are directed; the edge e=(x,y)originates at node x∈V and terminates at node y∈V.In this paper,the notation exyis used to denote an edge originating at node x and terminating at node y.Given an edge e,orig(e)determines the node from which e originates,and term(e)determines the node at which e terminates.Let g1=(V1,E1,α1,β1)and g2=(V2,E2,α2,β2)be two graphs to be matched. Example 1

A graphical representation of two graphs being matched is shown in Fig.1(b).These graphs have been derived from shape silhouettes,which are shown in Fig.1(a).Such a process might be applied, for example,to the recognition of mechanical parts in a manufacturing line.The appearance of noise in any part of the image capture process may mean that the derived graphs,such as the ones shown in Fig.1, do not match exactly.An inexact graph matching process is therefore required.

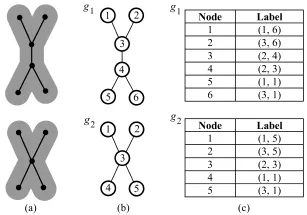
Fig.1　An example of two graphs to be matched.　(a)Shape silhouettes on which the graphs are based.(b)Derived graphs and node numbering.(c)Node labels.

Because the nodes in this example represent locations in 2D space,they have been labeled with 2D Cartesian coordinates(shown in Fig.1(c)). Edges are not labeled in this example;they capture only the structural information of the graphs.

The graphs shown in Fig.1 are used throughout this paper to illustrate various concepts of the proposed algorithm.In particular,forming sequences of correspondences and calculating the associated costs are described in Section 2.2.Transforming one graph into the other using graph edit operations is described in Section 2.3.Finding the minimum cost match by tree search is presented in Section 2.4. Identifying collapsible partial matches is presented in Section 2.5.Grouping collapsible partial matches is presented in Section 2.6.Collapsing for new graphs is presented in Section 2.7.The overall hierarchy of matching processes is described in Section 2.8.■

2.2Inexact graph matching

Let a correspondence be an association between a node v1∈V1in g1,and a node v2∈ V2in g2, (v1,v2)=V1×V2.Let C be the set of all possible correspondences between nodes in g1and nodes in g2.One node in a correspondence c may be the null node,Λ,which represents a node that is part of neither g1nor g2.A match,m,represents a sequence of correspondences Cm=(c1,c2,···),and a cost of forming its correspondences,mcost:

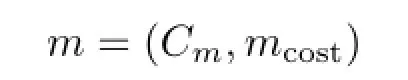
In other words,a match is a binary relation from a subset of V1,ˆV1⊆V1,to a subset of V2,ˆV2⊆ V2,along with the cost of performingsuch a mapping.A match’s cost is aligned with the degree of similarity of the nodes that appear in the correspondences(differences between the labels of corresponding nodes),and the subgraphs implied by the nodes that appear in the correspondences.

Note that the correspondences that appear in a match are dependent on the edges in both graphs, and the allowed graph edit operations(described in Section 2.3).While this research focuses on correspondences between graph nodes,it can easily be extended to include correspondences between graph edges.

Themethodofformingsequencesof correspondencesandcalculatingtheassociated costs is specific to the matching algorithm used. The method used in this research is discussed in the following sections.An optimal inexact graph matching algorithm is required to find the match that represents the optimal set of correspondences, where the optimal match is the match with the minimum global cost.A sub-optimal inexact graph matching algorithm,however,is in general only requiredtofindalocalminimum-costsetof correspondences.The local minimum may or may not be close to the global minimum.

Example 2

A sequence of correspondences for a match with a possible global minimum cost,for the graphs shown in Fig.1(b),is{(1,1),(2,2),(3,3),(4,3),(5,4),(6,5)}.■

2.3Graph edit operations

Oneoftheoldestandmostcommonlyused measures of match optimality is the graph edit distance.Graph edit distance defines the similarity of two graphs in terms of the minimum set of changes required to transform one graph onto the other.Graph edit operations are used to obtain the graph edit distance between two graphs.A sequence of graph edit operations is applied to one graph to transform it into the other graph.This sequence is implied by a match and its sequence of correspondences.Three types of graph edit operations may be used to transform any graph into another.These are node/edge substitution,deletion, and insertion.We define a mapping function f of a match m that places nodes of the two graphs into correspondence,determining Cm:

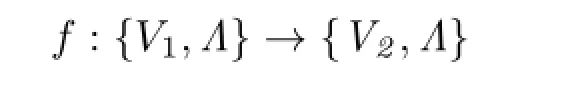
A node x∈V1is substituted for node y∈V2if f(x)=y.A node x∈V1is deleted from g1if f(x)=Λ,and a node y∈V2is inserted into g1if f−1(y)=Λ.

2.4Tree search algorithm

A tree(state space)search algorithm is often used to find the minimum cost match.The state spaceconsistsofanumberofstates,which represent matches,arranged in a tree structure.The match at the root of the state space contains no correspondences.The first layer of states represents matches with one correspondence,the second layer with two correspondences,and so on.Throughout this paper,the concepts of states and matches are used interchangeably in the context of the tree search algorithm.The tree search algorithm determines a cost of placing any two nodes into correspondence, ccost.The cost associated with any given match is equal to the sum of the costs of the match’s correspondences.

A state(other than the root state)is produced by embedding a new correspondence in the state’s parent state.We define a function ϕ that determines, for a given state and its associated match,the possible new correspondences that can be embedded in the match to form new child states.The form that ϕ takes is dependent on the specific tree search matching algorithm used.

Example 3

Various definitions of ϕ have been proposed in the literature.The following is an example that is similar to that used in Ref.[21].Let Vm,idenote the set of nodes in match m that belong to the graph gi,i∈{1,2}.Given m,ϕ returns correspondences between nodes in g1and nodes in g2that are currently not matched(i.e.,not in any correspondences of match m),and are connected by edges to nodes that are matched.In addition,correspondences between these nodes and Λ can be made:

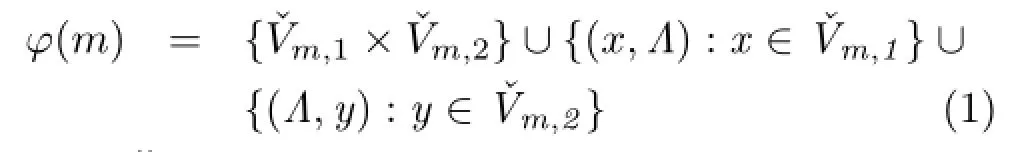
There are two considerations to take into account when defining this function:(1)it affects whether the optimal match can be found,and(2)it affects the number of matches produced in the state space. In many cases,these considerations are traded off against each other.For example,a large number of matches must often be produced in order to find the optimal match.It is highly desirable that the number of matches produced(searched)should be minimised,whilst guaranteeing that the optimal match will be found.

Thefirstoftheproposedchangesinthis researchistovastlyrestrictthenumberof correspondencesreturnedbyϕforanygiven match.The implementation of ϕ used in this research is based on that used by Eshera and Fu,given in Eq.(1).We simplify this definition of ϕ by preventing it from forming correspondences with Λ.This function therefore becomes:

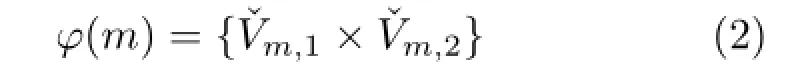
Modifying ϕ in this way has both the positive effect of reducing the number of matches in the state space,and the negative effect of reducing the algorithm’s ability to find the optimal match.In the following sections,we describe the methods that we use to ensure that the optimal match is found after simplifying ϕ in this way.

It should be noted that other definitions of ϕ may be used to implement the proposed algorithm.The goal is to simplify ϕ in such a way as to reduce the computational complexity of the matching process. The other requirement of ϕ is that“good”partial matches should still be found by the tree search algorithm.The importance of this requirement will become apparent later.

2.5Collapsibility criterion

During the tree search,partial matches will be produced that have a low cost.Such matches identify correspondences between nodes that have similar attributes,and similar relationships between corresponding nodes,but are incomplete.These matches are likely to appear in a complete match that has a low overall cost.The intention of the collapsibility criterion of the proposed method is to identify such partial matches,which we loosely term“good”partial matches.

The proposed simplification of ϕ has the effect ofpreventingstructuralalterationsduringthe matching process.Structural alterations are required to compensate for noise such as articulation and occlusion.The introduced collapsibility criterion reinstates the possibility of structural alterations, but only at certain points in the process.The collapsibility criterion allows structural alterations to occur where“good”low cost partial matches have been identified.Allowing structural alterations to occur at these points may be required to find the lowest cost complete match.It is impossible to provide an exact general definition of a“good”partial match,as it is application-specific.However, a“good”partial match should adhere to two properties:

1.Low cost.If the partial match has a low cost, then its correspondences are likely to appear in a complete match that has a low overall cost, which may be the global optimal match.

2.Minimumnumberofcorrespondences.To determine in a meaningful way that a partial matchislikelytoappearinalowcost complete match,it should contain a number of correspondences whose number is greater than or equal to a defined minimum number of correspondences.This also serves to improve the efficiency of the proposed method.

A mathematical example of the collapsibility criterion is given in Eq.(3).This example reflects the above properties of a“good”partial match,and gives an indication of the form that the collapsibility criterion may take.Results presented in Section 4 demonstrate the practicality of this form of collapsibility criterion.

Example 4

A “good”partial match for the graphs shown inFig.1(b)maycontainthesequenceof correspondences{(1,1),(2,2),(3,3)}.The cost of forming these correspondences would be low,yet the match contains some minimum number of correspondences(three).■

Identifying“good”partial matches is an important aspect of the proposed algorithm.For reasons that will become apparent,we label such matches collapsible during the creation of the state space. The condition that a match must satisfy in order to be labeled collapsible is called the collapsibility criterion:collapsible=f(m,g1,g2).

A partial match represents a match between subgraphs of the two graphs being matched.The collapsibility criterion therefore allows applicationspecific information at the subgraph scale to be applied to the matching process.

Example 5

The definition of the collapsibility criterion is largely application-specific.In this example,we define a“good”partial match as one that has a cost that is substantially lower than the cost of any of the match’s sub-matches,and has a number of correspondences that is greater than some threshold:

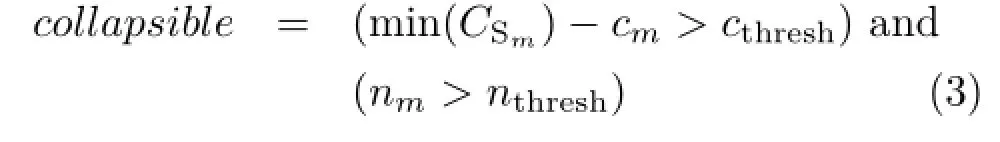
where m is the match being tested for collapsibility, CSmisthesetofcostsofthesub-matches ofmatchm,cmisthecostofmatchm, nmis the number of correspondences in match m,andcthreshandnthresharetheminimum thresholds for cost and number of correspondences, respectively.Using this collapsibility criterion, the match with correspondences{(1,1),(2,2),(3,3)} betweenthetwographsshowninFig.1(b) will be considered collapsible,as it has a small costincomparisontothecostofitssubmatches(e.g.,the match with correspondences {(1,1),(2,2),(3,3),(4,4)}),and it has the required number of correspondences,assuming suitable values for cthreshand nthresh.While the collapsibility criterion is application-specific,the example given in Eq.(3)is general enough to apply to many applications.■

In Example 5,two thresholds are used.While the collapsibility criterion is application-specific, it is likely that one or more thresholds will be needed.It is unfortunate that thresholds and application-specific heuristics are often introduced when a graph matching algorithm is used in a specific application.It will be interesting to see if future inexact graph matchings can remove such dependencies on thresholds.

2.6Combining collapsible partial matches

After collapsible matches are identified,they are combined to form groups of collapsible matches. This is done to realise“good”matches between groups of subgraphs.We define a grouping function, δ(Mc,g1,g2),which determines the possible groups of matches given a set of collapsible matches,Mc. The simple grouping function that we use in this research determines all possible combinations of collapsible matches such that no two matches in a combination have any common nodes:

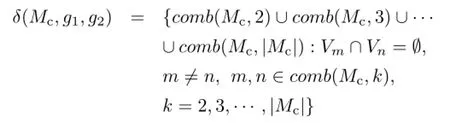
wherecomb(Mc,i)denotesthesetofallicombinations of set Mc,and Vjdenotes the set of nodes in match j.

Note that this step may not be strictly necessary; the optimal match will be found without applying a grouping function.However,this step allows the representation of application-specific information across matched subgraphs,which may be useful in some applications,and may serve to reduce the running time of the proposed algorithm.

2.7Collapsing for new graphs

For each group of collapsible matches,a collapse operation is performed on g1and g2,in order to form new graphs,and.The purpose of the collapse operation is to preserve the fact that matches are“good”,so that the remainder of the nodes in the two graphs can be matched with this knowledge. As discussed earlier,collapsing also allows matching to continue from different parts of the two graphs, allowing for structural alterations.

A collapse operation is performed for both graphs being matched,given a group of collapsible matches. In summary,for each graph,a new graph is produced that is identical to the original graph with exceptions regarding those nodes that appear in the group of collapsible matches.For each collapsible match in the group,the matched nodes are replaced by a single node in the new graph with a label that is derived from the labels of the original nodes in the match.Edges in the original graph are either deleted,modified,or copied directly to the new graph,depending on the originating and terminating nodes of each edge.This process is defined formally in the remainder of this section.

Let a new graph created by a collapse operation bewhere i∈{1,2}identifies the graph undergoing the collapse operation.Letdenote a group of collapsible matches,andheset of nodes inMˆ that belong to the graph gi.denotes the set of nodes in graph gi,that belong to a particular collapsible match j.The set of nodes in the new graphis defined as

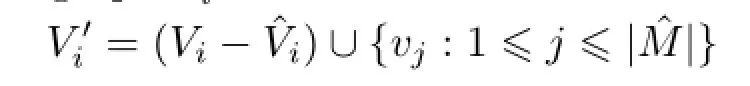
where vjare new nodes,each of which replaces a set of nodes of a collapsible match.Letdenote the new nodes in graphThe set of edges in the new graph is defined as follows:

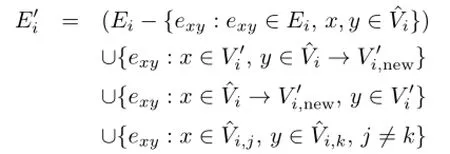
In essence,the edges in the new graph consist of those in the original graph with the exception of those between collapsed nodes,and with the addition of those that are from existing nodes to new nodes, from new nodes to existing nodes,and from new nodes to new nodes.Note that an edge exyfrom the original graph does not appear in the new graph if both its originating node,x,and its terminating node,y,are part of the same match being collapsedand,where j=k).

The node labeling function foris the same as for gi,except where nodes are being collapsed and are replaced by new nodes.Where new nodes are being labeled,α＇will be application-specific,and will typically assign labels that are derived from the labels of the nodes in the original graph that is undergoing the collapse operation.The node labeling function for the new graph is defined as follows:

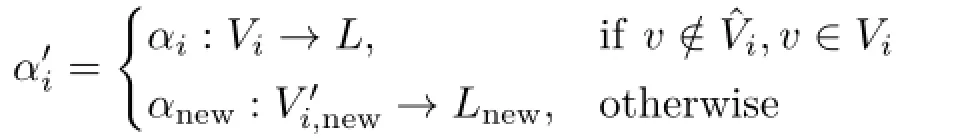
where Lnewis an alphabet of labels for new nodes and edges.αnewis essentially used to coalesce the labels of the nodes being collapsed,and perhaps the labels of the edges between those nodes,into a single label for the new node.

The edge labeling function foris the same as for gi,except where one or both of an edge’s originating and terminating nodes are new nodes formed through the application of the collapse operation.When either of these nodes are new nodes,β＇will be application-specific,and will typically assign labels that are derived from the labels of the nodes that the edge connects or,if applicable,the label(s)of the edge(s)that the new edge replaces.The edge labeling function for the new graph is defined as follows:

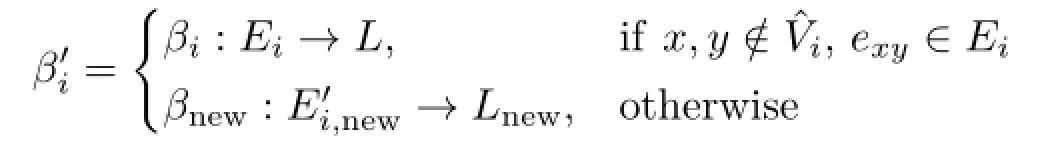
Example 6

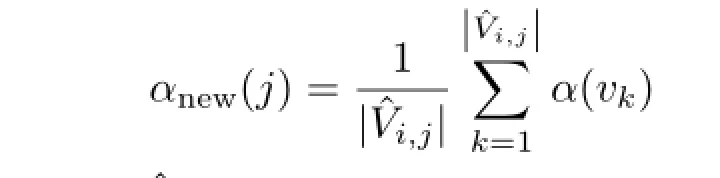
where vk∈ˆVi,j.Here,the node labels are treated as 2D vectors that,in the above equation,undergo vector addition and scalar multiplication.As an example,if nodes 1,2,and 3 of graph g1in Fig.1(b) were to be collapsed,the lab?el of t?he resulting node in the new graph would be

2.8Hierarchy of matching processes

The overall algorithm,which uses the previously defined steps,will now be described with reference to Fig.2.The two graphs are first matched using a matching process that has been simplified in the manner described in Section 2.4(1 in Fig.2).This matching process is referred to as Matching Process 0 in Fig.2.A portion of this matching process is shown in the figure,with the correspondences of some of the states that are produced,and the costs associated with these states.During the matchingprocess,matches are marked as collapsible if they satisfy the collapsibility criterion.The state of one such collapsible match is State 3 of Matching Process 0.A number of combinations of collapsible matches are then formed.Each match in a combination represents a subgraph of g1,and a subgraph of g2. Collapsing a combination is the process of deriving two new graphs from g1and g2,denoted byandThe process of collapsing State 3 of Matching Process 0 is shown as 2 in Fig.2.

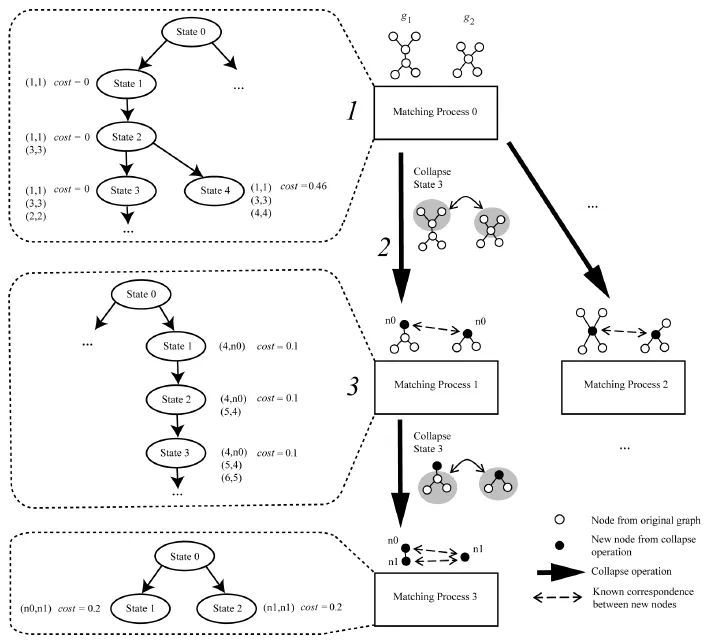
Fig.2　The proposed hierarchy of matching processes,applied to the example graphs of Fig.1.n0 and n1 identify new nodes that are created by applying the collapse operation.

In Fig.2,nodes are labeled with 2D Cartesian coordinates.These labels are used to calculate the cost of forming each correspondence,in each match in the state space.The initial correspondences formed for the states in the first level of the state space incur no cost.The cost of forming a new correspondence is determined by first measuring the average direction from nodes previously put intocorrespondencetothenodesinthenew correspondence,for each graph.The cost is then the absolute difference between these two directions. Other cost functions can be defined in a similar way, for other forms of node and/or edge labels.More details can be found in Ref.[22].■

With each collapse operation,the original graphs arechangedinsomeway,withthegoalof finding a match that represents a more optimal set of correspondences.Just as each correspondence formed by a matching process incurs a cost,a collapse operation must also have an associated cost or penalty.This cost is added to the cost of allmatches formed by any matching process that is the result of applying the collapse operation(line 10 of Algorithm 1).For example,referring to Fig.2,any matches produced by Matching Process 1,or any of its descendants in the hierarchy,will incur the cost of performing the collapse operation at step 2 in the diagram.In this research,and in the example shown in Fig.2,the cost of performing a collapse operation is set to a fixed value(0.1 in the diagram).However, it may easily be a function of the matches being collapsed.Once the hierarchy of matching processes has been constructed,the optimal match is simply the match with the lowest overall cost.

Algorithm 1:Hierarchical graph matching procedure

The proposed method differs from the traditional inexact graph matching method in two main ways. Firstly,the proposed method simplifies ϕ,which drasticallyreducesthenumberofstatesthat are searched by a single matching process and consequently removes the guarantee of optimality. Optimality is restored using the second aspect of the proposed method:the collapsibility criterion and hierarchical matching processes.The collapsibility criterion allows additional states to be searched that will possibly lead to the optimal solution.The guarantee that the optimal solution is found amongst the additional states is dependent on the applicationspecific collapsibility criterion;the criterion must identify those states that can lead to the optimal solution.If this condition is satisfied,the optimal solution is guaranteed to be found.

Ingeneral,thecollapsibilitycriterionis application-specific.In designing the collapsibility criterion,it is useful to consider the sources of noise that are likely to appear in the chosen application,that will cause differences between graphsrepresentingsimilarinformation.These sources of noise include articulation,occlusion, changes in viewpoint,and spurious noise that may cause additional nodes and/or edges in one or both graphs being matched.

It may seem that the proposed method depends heavily on knowledge of the chosen application.It is true that additional application-specific knowledge is required to implement the proposed collapsibility criterion,and that this may effect the optimality of the proposed method.In practice,however, theapplicationwillalwaysbeknown.Many known optimisations,such as A*,utilise additionalapplication-specific knowledge to achieve the same goals(gains in efficiency).Relaxation-based methods require additional information in order to determine good initial assignments or probabilities.We have found that a simple collapsibility criterion that has the properties discussed in Section 2.5 is tolerant toward noise,produces the optimal solution,and reduces the time taken to find the match.

3　Computational complexity analysis

3.1Standard tree search

Inthissection,weanalysethecomputational complexity of a typical inexact graph matching algorithm using tree search.We use the definition of ϕ that is similar to Eshera and Fu’s,given in Eq.(1).While this makes the following analysis specific to one particular algorithm,this algorithm is typical of many.We aim only to capture the general complexity of a class of algorithms so that the benefits of the proposed method can be demonstrated.

As before,let g1and g2be two graphs being matched.Let n1and n2be the number of nodes in g1and g2,respectively.For the purpose of this analysis, we assume that all edges are bi-directional,and that both graphs are fully-connected.We also assume that all states in the tree must be searched to find the optimal solution,which allows us to analyse the algorithm as a depth-first tree search algorithm.The computational complexity of depth-first tree search algorithm,as given by Ref.[23],is O(bm),where b is the branching factor(the maximum number of successors of any state in the tree),and m is the maximum depth of any state in the tree.

The upper bound on b occurs when a single pair of nodes has been put into correspondence(the first level in the tree).A state with maximum depth m is produced by applying a sequence of correspondences between a node in g1and Λ,followed by a sequence of correspondences between Λ and a node in g2,or vice versa.These correspond to the second and third sets in the union of sets of ϕ,shown in Eq.(1). We can apply n1or n2of these correspondences followed by n2or n1of these correspondences. The computational complexity of the standard tree search algorithm,subject to the exact definition of ϕ is therefore:

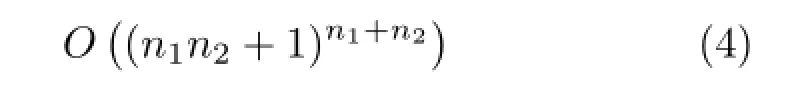
3.2The proposed algorithm

The proposed algorithm uses a matching process with a lower computational complexity,but involves the use of multiple matching processes.As discussed in Section 2.8,the matching processes are arranged in a hierarchy(tree).The overall algorithm may therefore also be analysed as a depth-first tree search algorithm.The computational complexity of the

The branching factor for the overall hierarchy,bh, is the maximum number of sub-matching-processes produced by a single matching process through applying the collapse operation.This has a one-toone correspondence with the maximum number of groups of collapsible states produced by a matching process,and therefore depends on the number of collapsible matches produced.The chosen definitions of ϕ and δ(the grouping function)therefore play a role.Since the number of nodes in each graph, and therefore the number of states in each matching process,reduce as the depth in the hierarchy increases,the upper bound on the branching factor applies to the first(root)matching process in the hierarchy.bhcan be derived by analysing the number of collapsible matches produced by the root matching process.The maximum depth of any matching process in the hierarchy,mh,occurs when a sequence of collapses of single-match groups of collapsible matches is performed,and each match being collapsed contains the minimum number of nodes from each graph,nthresh.

We now turn our attention to the complexity of a single matching process within the hierarchy of matching processes.Recall that the proposed algorithmaimstoreducethecomputational complexity of a single matching process.If we simplify ϕ as described in Section 2.4,that is, weremovethealgorithm’sabilitytoperform correspondences of nodes in either graph with Λ,the branching factor of a single matching process can easily be found.The maximum depth of a state in asingle matching process,mp,occurs when a sequence of correspondences between a node in g1and a node in g2are made,in the root matching process of the hierarchy.The overall computational complexity of the proposed algorithm,subject to choice of ϕ,is

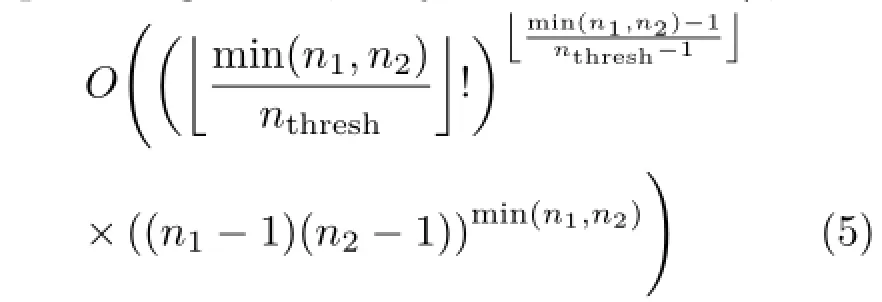
In our analysis of this complexity,a number of simplifications have been made.Equation(5) provides an absolute worst-case complexity.In a real application,the branching factor and maximum depth will typically be much smaller than the worst case.

3.3Computational complexity comparison

Tomoreeasilycomparethecomputational complexity of the two algorithms,we input various values of n1and n2into Eq.(4)and Eq.(5)to give upper bounds on the number of matches produced. The value of nthreshfor the proposed method is also varied.These comparisons are shown in Table 1.

Observethattheworst-casecomputational complexity of the proposed algorithm is much smaller than the standard tree search algorithm.By increasing nthresh,we can significantly reduce the number of matches produced(as there will be fewer collapsible matches in each state space).However, depending on the application,increasing nthreshmay reduce the algorithm’s ability to find the optimal match.In this research,a value of three has proved to be the most useful.

4　Experimental results

This section presents some results of the proposed algorithm,in comparison with two previous optimal inexact graph matching algorithms that are based ongraph edit operations.The proposed method is then extended to produce sub-optimal solutions,and is compared with a recent sub-optimal shape matching method.To distinguish the optimal and sub-optimal variants of the proposed method,this section refers to them as the“optimal proposed method”and the“sub-optimal proposed method”,respectively.

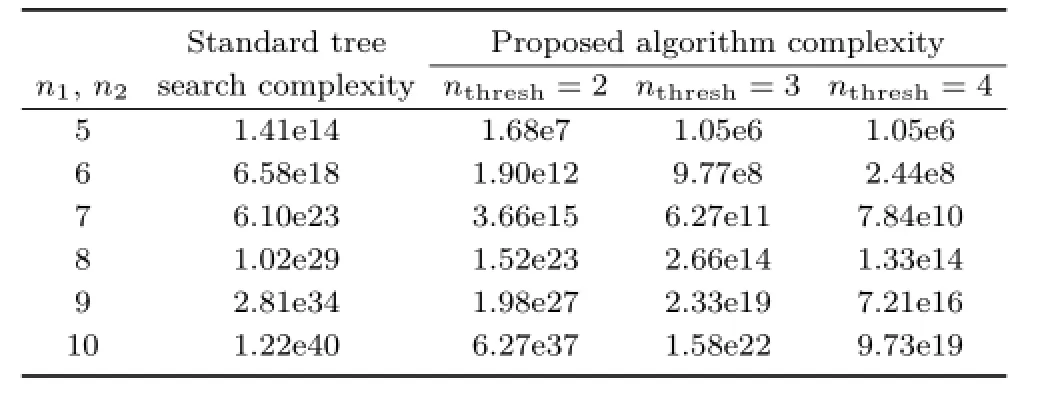
Table 1　Computational complexity comparison

The cost function used for the proposed method and other optimal methods is described in Example 7.A fixed cost of 0.1 is used for correspondences between one node from either graph,and the null node.The collapsibility criterion used is described in Example 5,with cthreshand nthreshset to 0.1 and 3,respectively.All collapse operations incur a fixed cost of 0.1.All algorithms have been implemented using the C++programming language,and have been tested with a 2.52 GHz Intel CPU with 3.5 GB of RAM.

4.1Optimal inexact graph matching

Inthissection,theoptimalproposedmethod is compared with other optimal inexact graph matching methods.The purpose of this section is to show the benefits of the proposed method when searching for the optimal solution.The first of the previous optimal algorithms chosen for comparisons is due to Eshera and Fu[21].This seminal algorithm utilises a state-space search method such as the one described in Section 2.4,and performs graph edit operations of node insertion,node deletion,and node substitution.This algorithm is typical of many inexact graph matching algorithms in the literature.

The second previous optimal algorithm chosen for comparison is that of Berretti et al.[24]. Berretti et al.use an additional“node merging”operation,whichessentiallyreplacesasetof connectednodeswithanewnode.Whereas the proposed algorithm implements a merging-like operation between matching processes,Berretti et al.perform their node merging operation as part of a single matching process.The addition of this operation therefore increases the complexity of a single matching process.The suboptimal heuristic also proposed by Berretti et al.is explored in Section 4.2.

These two previous algorithms have been chosen forcomparisontohighlighttherolethatthe employed graph edit operations and the complexity of ϕ,play in determining the time taken to perform amatch.We believe that,while the adverse influence of the number of graph edit operations on match time may be apparent to those in the field,this influence has received rather little analysis.The following results demonstrate this effect and the proposed algorithm’s ability to reduce it.Since all three methods compared in this section are optimal, we compare match time only.

4.1.1Shape matching

The three optimal methods are first tested using shapes from the Kimia-216 shape database[25].The graphs input to the three methods are derived from the skeletons of shape silhouettes.A sample of the shape silhouettes from the Kimia-216 database are shown in Fig.3 with their derived graphs overlaid.The shape skeletons were extracted using the method described by Morrison and Zou[26].The nodes of the derived graphs correspond to skeleton junction and end points,and the edges of the derived graphs correspond to the skeleton branches between junction and end points.The positions of the nodes in the plane are used for node attributes,and are therefore used to calculate the costs of forming correspondences between nodes.

Fig.3　A sample of shapes from the Kimia-216 database and their derived graphs.

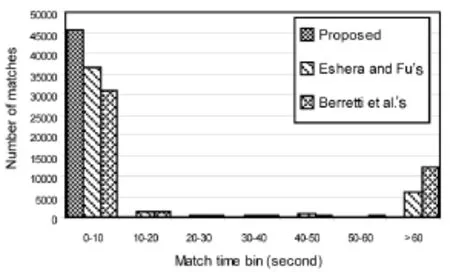
Fig.4　Histograms of match time for matching shapes from the Kimia-216 database,using the optimal proposed method,Eshera and Fu’s,and Berretti et al.’s.

Figure 4 shows a histogram of the match time using the three optimal methods for shapes from the Kimia-216 database.The optimal proposed method performs almost all matches in under 10 seconds.While this is mostly true for the other methods,a significant number of their matches are not made in reasonable time(taking longer than 60 seconds).We have also observed(though it is not shown)that the proposed method always takes a shorter time than these previous methods to perform any given match.Also,the method of Eshera and Fu matches most combinations of graphs faster than that of Berretti et al.,who introduce an additional operation.This demostrates the influence of the number of available graph edit operations on the complexity of the function that determines each state’s successors.The proposed method’s simplification of a single matching process more than offsets the additional time introduced by performing multiple matching processes.

4.1.2Random graphs

In order to more fully test the proposed algorithm,“random”graphs were used to test the three optimal algorithms.The number of nodes and edges in each graph was controlled,while the node labels and configuration of edges were randomised. What resulted were graphs with known sizes,but varying complexity.The purpose of these tests is to demonstrate the limitations of the three algorithms in a controlled setting.

Figure 5 shows a plot of the average match time for each of the algorithms,as the number of nodes in the graphs is increased.For a given number of nodes and edges,five graphs were generated.The node attributes,and the originating and terminating nodes of each edge,were randomised.The node attributes are,once again,2D Cartesian coordinates, selected in the range 0.0 to 5.0 in the x-andy-directions.Each graph is matched only with other graphs with the same number of nodes and edges.Results of matching graphs with different characteristics are presented in Section 4.1.1.

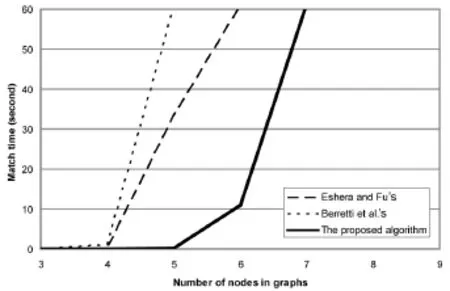
Fig.5　Match time vs.number of nodes for random graphs.Runs taking longer than 60 seconds are aborted.

All three algorithms are able to complete matching in a reasonable time when the number of nodes in the graphs is small(four or fewer nodes).As the number of nodes is increased,there is a point at which any algorithm becomes unable to complete in under 60 seconds.The optimal proposed method is faster than the two previous methods,but fails to perform the match in a reasonable time with some number of nodes(seven nodes).This is due to the inherent complexity of the inexact graph matching process, which is retained by the proposed algorithm.

Note that we have presented here match time for three algorithms implemented without the use of heuristics or estimations to guide the search;all three algorithms perform an exhaustive search of the state space.This has been done in order to more clearly demonstrate the effect that available operations has on match time,and the advantages of the proposed method.

4.2Sub-optimal inexact graph matching

In the previous section,the proposed method was compared with two other optimal methods that are based on tree search and graph edit operations.While the proposed method shows a clear advantage in terms of match time,it cannot escape the underlying high computational complexity of optimal matching.In this section,we compare the optimal proposed method with two other matching methodsthataresub-optimal.Thefirstsuboptimal method is the(optimal)proposed method augmented with a simple technique proposed by Berretti et al.[24]for improving match speed while producing only a sub-optimal solution.We name this method the“sub-optimal proposed method”,as opposed to the“optimal proposed method”.The second sub-optimal method is the method of Bai and Latecki[5].Bai and Latecki also use shape skeletons to match shapes,but their technique is somewhat different.Their approach is to compare shape widths sampled from the shortest“skeleton paths”between pairs of end points,and they do not consider skeleton junction points or the structure of the skeleton explicitly.Despite the different approaches of these methods,comparing their results allows us to evaluate the proposed method in the context of shape matching,and the state of the art in this field.We set all parameters of Bai and Latecki to those values given in Ref.[5].All methods are compared in terms of accuracy using the Kimia-216 shape database.The sub-optimal algorithms tested always produce a match quickly(usually in less than one second),so a comparison in terms of match time is not given.

Out of 2376 matches(the 11 closest matches for each of the 216 shapes),the optimal proposed method matches 767 shapes from the same category as the query shape.The retrieval rate of the optimal proposed method for the Kimia-216 database is therefore 32.3%.Using similar calculations,the suboptimal proposed method and the method of Bai and Latecki have retrieval rates of 31.8%and 34.8%, respectively.While these retrieval rates do not appear promising,it should be noted that they apply to the current use of the proposed method in the shape matching application.The performance of the three methods for the shape matching application is explored in more detail in the remainder of this section,and various improvements are proposed.

Figure 6 shows a selection of matches made using the optimal proposed method.The optimal proposed method performs reasonably well for most shapes,considering it utilises skeleton information only.Contour information,while used to produce the skeleton,is not used by the proposed matching algorithm directly.In addition,the implementation of the proposed method uses the simple cost function described in Example 7 that is based purely on relative angle differences.The results shown in Fig.6 should therefore be evaluated in terms of the underlying graphs only.For the shape matchingapplication,the proposed method can potentially be improved with a more sophisticated cost function that utilises more information.

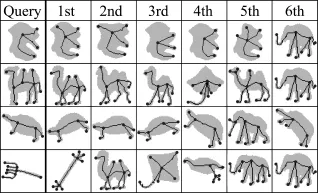
Fig.6　Selected results of the proposed method on the Kimia-216 database.

The proposed method can easily be modified to produce a sub-optimal solution in much shorter time,if required.Berretti et al.[24]have chosen to explore only the best cost match of the possible next matches at each iteration.This means that there are many branches of the state space that are left unsearched,one of which may contain the global optimal match.To demonstrate that the proposed method can be extended to provide a sub-optimal solution if required,it is modified using the approach taken in Ref.[24].Sample results from this method are shown in Fig.7.The results from the suboptimal proposed method deviate slightly from those of the optimal proposed method.Overall,the suboptimal proposed method is not as accurate as the optimal proposed method,in terms of matching the underlying graphs.However,in most cases,the difference is not significant.

As mentioned previously,the implementation of the proposed method does not consider shape contour information explicitly during the matching process.This clearly affects the results,from the perspective of matching shape silhouettes.Bai and Latecki have recently proposed a shape matching method that uses shape skeletons combined with shape widths at equidistant locations along skeleton paths between endpoints.Some results from testing this method using the same shapes from the Kimia-216 database are shown in Fig.8.

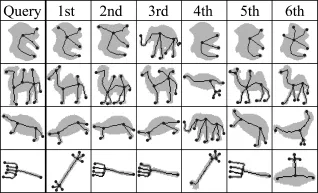
Fig.7　Selected results of the sub-optimal proposed method, modified using a“best-only”state space search method,on the Kimia-216 database.

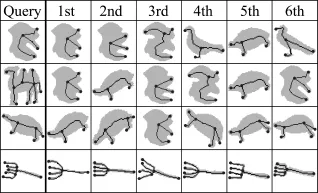
Fig.8　Selected results of the shape matching method of Bai and Latecki[5]on the Kimia-216 database.

For the shape silhouette matching task,the method of Bai and Latecki outperforms both the optimal and sub-optimal proposed methods in most cases.The overall retrieval rate of Bai and Latecki is also slightly higher than the proposed method. We believe that this is because they make use of important shape contour information directly in the matching process.We note that we could not obtain the outstanding results given by Bai and Latecki[5]. This is most likely due to the use of a different skeletonization method.Shape matching accuracy is heavily dependent on both the shape representation (in this case,the skeleton)and the shape matching method itself.To achieve high accuracy,the shape representation and matching method must be closely aligned.

There are some cases where the method of Bai and Latecki clearly does not produce accurate results. Bai and Latecki do not use structural information contained in the skeleton.This appears to put their method at a disadvantage for some shapes,such as the second query shape of Fig.8.Here,the skeleton captures the structure of the underlying shape but,because the shape does not consist primarily of ribbon-like parts,shape widths along skeleton branches may not be a good representation of contour information.The skeleton representation is known to be of most utility when representing ribbon-like shapes.The fourth query shape in Fig.8, on the other hand,consists entirely of ribbon-like parts and the method of Bai and Latecki performs extremely well.This highlights that,while placing more emphasis on shape structure definitely adds complexity,it is required for robust shape matching.

Finally,we illustrate the applicability of the proposed method to the text character recognition problem.Fromamatchingperspective,text characters are somewhat different to the shapes contained in the Kimia-216 database.Because textcharacters consist mainly of strokes of comparatively uniform width,structural information must play a key role in matching.Furthermore,text characters often contain loops,which presents problems to many matching methods.Figure 9 shows some results of matching in a database of eight characters (“a”to“h”)from six different fonts.

Whiletheproposedinexactgraphmatching algorithm can match graphs containing loops or cycles,the current application of the algorithm to the shape matching problem does not capture shape loops effectively(observe results for the“b”character in Fig.9).The graphs derived from shape skeletons contain nodes placed on skeleton junctions and end points only.To capture loops,nodes must be placed on skeleton branches(e.g.,at locations of high curvature),or graph edges must somehow represent positions along branches.The proposed inexact graph matching algorithm can easily accommodate such additional information.Loops appear to play a large role in differentiating text characters,and are therefore a very important aspect of the character recognition problem.

4.3Discussion

Whilesub-optimalmethodsoutperformthe proposedmethodandotheroptimalmethods in terms of match time,some sacrifice in quality is made.The sub-optimal proposed method performs well in most cases,and shape matching retrieval rates are similar.However,when results are analysed in terms of the graph information only,the suboptimal proposed method is not as accurate as the optimal proposed method.

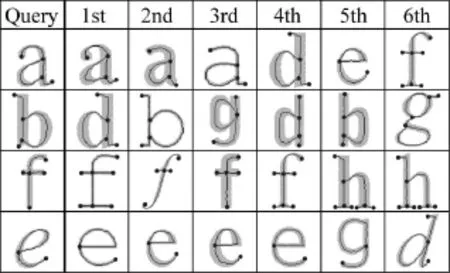
Fig.9　Selected results of the proposed method on a text character database.

The proposed method matches nodes in a way that corresponds with a human’s perception of the graph structures.However,in order to match shape silhouettes in a more meaningful way,contour information must be used directly in the matching process.The simple cost function used in this application of the proposed method does not consider shape contour information.The absence of this information is reflected in the results.In future research,the cost function used here will be extended to include contour information.

Whilecontourinformationappearstobe important for matching shapes from the Kimia-216database,structuralinformationismore importantfortextcharacterrecognition.The relative importance of contour and structural shape information varies depending on the type of shapes being matched.A balance between the two is clearly required for generic shape matching.The proposed method’s performance in text character matching canfurtherbeimprovedbyusingadditional skeleton-based information(such as nodes in areas of high curvature)to aid in differentiating characters that contain loops.

The proposed method,being based on early attributedrelationalgraph(ARG)matching methods,can easily be extended in these directions without any change to the underlying algorithm. These changes will improve the proposed method’s performance in the application of shape matching.

Most recent work on inexact graph matching has attempted to produce good sub-optimal solutions. This paper takes a very different approach,and attempts to reduce the complexity of finding the optimal solution.Such an approach is,of course, beneficial only if the optimal solution is required or presents a significant improvement over the expected sub-optimal solution.The results shown in this section demonstrate both the advantages and disadvantages of the proposed approach:there is a limit to the size of the graphs that can be matched, but it produces better results than a sub-optimal method in many cases.We believe that optimal solutions are of high interest to the community, and that finding optimal solutions will become more feasible in the near future.

It may be argued that the inexact graph matching problem itself implies uncertainty,and therefore an optimal solution is not necessary.However,we argue that the uncertainty inherent in the problem itselfshould be separated from the uncertainty incurred by the matching algorithm.The ultimate goal of a matching algorithm is to determine how similar two graphs are.Erroneous or sub-optimal results may have a detrimental effect on the decisions made using such similarity measures.Many applications, such as handwriting recognition or optical character recognition(OCR),relyonaccuratesimilarity measures in order to match shapes correctly.

Wehavealreadymentionedthatreducing the complexity of computationally-intensive graphtheoretic algorithms is gaining renewed interest. Also,with the increasing use of parallel processing techniques,computationally-intensivealgorithms designedforsuchparallelismwillmakemany previously-intractable methods useful.The proposed method is amenable to such techniques,which will be used to develop the proposed method in future research.

5　Conclusions

In this paper,we have proposed a method of reducingthecomputationalcomplexityofthe inexact matching process.The proposed method is able to produce the optimal solution,subject to an application-specific criterion that operates at the subgraph level.Experimental results and a comparison of the computational complexity of the proposed algorithm with a previous algorithm that is based on tree search demonstrate that our aim has been achieved.

We believe that this work contributes significantly to the community,by proposing an approach to the inexact graph matching problem that is substantially different to the existing literature,demonstrating the method’s application to a common use of inexact graph matching,and demonstrating the method’s potential use in other applications by including an estimation that allows for sub-optimal matches.For the application of shape matching,various potential improvements to the implementation of the proposed method are discussed.

While the implementation presented in this paper is based on the tree search algorithm of a particular previous study,we believe that the technique may be expanded to other methods of performing inexact graph matching.These ideas may even be extended to inexact graph matching algorithms that are not based on tree search and graph edit operations.This is an area for future research.By breaking the overall matching process down into a number of smaller matching processes,the proposed method can easily be implemented with parallel processing in mind.

Results show that the proposed method is able to match graphs with more nodes in a reasonable amount of time.

Acknowledgements

The authors wish to express their gratitude to associate professor Weidong(Tom)Cai at the University of Sydney in Australia for his advice and help in relation to the publication of this article.

OpenAccessThis article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited.

References

[1]Conte,D.;Foggia,P.;Sansone,C.;Vento,M.How and why pattern recognition and computer vision applications use graphs.In:Studies in Computational Intelligence,Vol.52.Kandel,A.;Bunke,H.;Last,M. Eds.Springer-Verlag Berlin Heidelberg,85-135,2007.

[2]Hu,S.-M.;Zhang,F.-L.;Wang,M.;Martin,R. R.;Wang,J.PatchNet:Apatch-basedimage representation for interactive library-driven image editing.ACM Transactions on Graphics Vol.32,No. 6,Article No.196,2013.

[3]Vento,M.;Foggia,P.Graph matching techniques for computer vision.In:Graph-Based Methods in Computer Vision:Developments and Applications. Bai,X.;Cheng,J.;Hancock,E.Eds.IGI Global,1-41, 2012.

[4]Wang,M.;Lai,Y.-K.;Liang,Y.;Martin,R.R.;Hu, S.-M.BiggerPicture:Data-driven image extrapolation using graph matching.ACM Transactions on Graphics Vol.33,No.6,Article No.173,2014.

[5]Bai,X.;Latecki,L.J.Path similarity skeleton graph matching.IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.30,No.7,1282-1292,2008.

[6]Tsai,W.-H.;Fu,K.-S.Error-correcting isomorphisms of attributed relational graphs for pattern analysis. IEEE Transactions on Systems,Man and Cybernetics Vol.9,No.12,757-768,1979.

[7]Tsai W.-H.;Fu,K.-S.Subgraph error-correcting isomorphisms for syntactic pattern recognition.IEEE Transactions on Systems,Man and Cybernetics Vol. 13,No.1,48-62,1983.

[8]Berretti,S.;Bimbo,A.D.;Vicario,E.Efficient matching and indexing of graph models in contentbasedretrieval.IEEETransactionsonPattern Analysis and Machine Intelligence Vol.23,No.10, 1089-1105,2001.

[9]Nilsson,N.J.Problem-solving Methods in Artificial Intelligence.McGraw-Hill Pub.Co.,1971.

[10]Christmas,W.J.;Kittler,J.;Petrou,M.Structural matchingincomputervisionusingprobabilistic relaxation.IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.17,No.8,749-764, 1995.

[11]Gold,S.;Rangarajan,A.A graduated assignment algorithm for graph matching.IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.18,No. 4,377-388,1996.

[12]Conte,D.;Foggia,P.;Sansone,C.;Vento,M. Thirty years of graph matching in pattern recognition. International Journal of Pattern Recognition and Artificial Intelligence Vol.18,No.3,265-298,2004.

[13]Foggia,P.;Percannella,G.;Vento,M.Graph matching and learning in pattern recognition in the last 10 years.International Journal of Pattern Recognition and Artificial Intelligence Vol.28,No.1,1450001, 2014.

[14]Livi,L.;Rizzi,A.The graph matching problem. Pattern Analysis and Applications Vol.16,No.3,253-283,2013.

[15]Gregory,L.;Kittler,J.Using graph search techniques for contextual colour retrieval.In:Lecture Notes in Computer Science,Vol.2396.Caelli,T.;Amin,A.; Duin,R.P.W.;de Ridder,D.;Kamel,M.Eds. Springer-Verlag Berlin Heidelberg,186-194,2002.

[16]Eppstein,D.Quasiconvex analysis of multivariate recurrenceequationsforbacktrackingalgorithms. ACM Transactions on Algorithms Vol.2,No.4,492-509,2006.

[17]Fomin,F.V.;Grandoni,F.;Kratsch,D.Measure and conquer:Domination—A case study.In:Lecture Notes in Computer Science,Vol.3580.Caires,L.;Italiano, G.F.;Monteiro,L.;Palamidessi,C.;Yung,M.Eds. Springer-Verlag Berlin Heidelberg,191-203,2005.

[18]Fomin,F.V.;Grandoni,F.;Kratsch,D.;Lokshtanov, D.;Saurabh,S.Computing optimal steiner trees in polynomial space.Algorithmica Vol.65,No.3,584-604,2013.

[19]Van Rooij,J.M.M.;Bodlaender,H.L.Exact algorithms for edge domination.Algorithmica Vol.64, No.4,535-563,2012.

[20]Woeginger,G.J.Exact algorithms for NP-hard problems:A survey.In:Lecture Notes in Computer Science,Vol.2570.J¨unger,M.;Reinelt,G.;Rinaldi, G.Eds.Springer-Verlag Berlin Heidelberg,185-208, 2003.

[21]Eshera,M.A.;Fu,K.-S.A graph distance measure for image analysis.IEEE Transactions on Systems,Man and Cybernetics Vol.14,No.3,398-408,1984.

[22]Morrison,P.Shape matching based on skeletonisation and inexact graph matching.Ph.D.thesis.Western Sydney University,2011.

[23]Russell,S.;Norvig,P.Artificial Intelligence:A Modern Approach.Prentice-Hall,1995.

[24]Berretti,S.;Bimbo,A.D.;Pala,P.A graph edit distance based on node merging.In:Lecture Notes in Computer Science,Vol.3115.Enser,P.;Kompatsiaris, Y.;O’Connor,N.E.;Smeaton,A.F.;Smeulders,A. W.M.Eds.Springer-Verlag Berlin Heidelberg,464-472,2004.

[25]Sebastian,T.B.;Klein,P.N.;Kimia,B.B. Recognition of shapes by editing shock graphs.In: Proceedings of the 8th IEEE International Conference on Computer Vision,Vol.1,755-762,2001.

[26]Morrison,P.;Zou,J.J.Triangle refinement in a constrained Delaunay triangulation skeleton.Pattern Recognition Vol.40,No.10,2754-2765,2007.

Paul Morrison completed his Ph.D. degree in 2011 at the Western Sydney University,Australia,whilst studying topics in image processing and shape recognition.Hecurrentlypursues research and development at CiSRA in Sydney,Australia,and is a member oftheInstituteofElectricaland Electronics Engineers(IEEE).

Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095. To submit a manuscript,please go to https://www. editorialmanager.com/cvmj.

1School of Computing,Engineering and Mathematics, WesternSydneyUniversity,LockedBag1797, Penrith,NSW 2751,Australia.E-mail:P.Morrison, pwmorrison@gmail.com;J.J.Zou,J.Zou@ westernsydney.edu.au().

Manuscript 2015-10-26;accepted:2015-11-24

JuJiaZou his B.S.and M.S.degreesinradio-electronics fromZhongshanUniversity(also knownasSunYat-SenUniversity) in Guangzhou,China,in 1985 and 1988,respectively,and Ph.D.degree inelectricalengineeringfromthe UniversityofSydney,Australia,in 2001.Currently,he is a senior lecturer with School of Computing,Engineering and Mathematics at Western Sydney University,Australia.He was a research associate and then an Australian postdoctoral fellow at the University of Sydney from 2000 to 2003.His research interests include image processing,pattern recognition,computer vision, and their applications.He has been a chief investigator for a number of projects funded by the Australian Research Council.He is a member of the Institute of Electrical and Electronics Engineers(IEEE).