冻融循环下轴心受压砖砌体损伤本构关系模型
商效瑀,郑山锁,徐 强,刘春成
(1.东北电力大学 建筑工程学院,吉林 吉林 132012;2.西安建筑科技大学 土木工程学院,陕西 西安 710055;3.长安大学 地质工程与测绘学院,陕西 西安 710064)
目前,国内外对混凝土本构关系的研究丰富且成熟,而对于(砖)砌体本构关系的研究则相对滞后,仍停留在弹性本构关系模型[1-3]及经验本构关系模型[4-5]上.值得注意的是,关于冻融循环下轴心受压砌体损伤本构关系模型国内外均未见相关报道.冻融循环下轴心受压砌体损伤本构关系模型不仅是开展寒冷地区砌体结构有限元模拟的必要基础,同时也是进行寒冷地区在役砌体结构耐久性评估的重要依据,可填补现阶段寒冷地区砌体结构耐久性理论研究的空白.
本文基于损伤力学理论和应变等价原理,将冻融循环下轴心受压砌体损伤等效为冻融损伤和轴心受压损伤的非线性耦合,推导了砌体冻融损伤和轴心受压损伤演化方程,获得了冻融循环下轴心受压砌体损伤演化方程,建立了冻融循环下轴心受压砌体损伤本构关系模型,然后利用冻融循环后砌体轴心受压试验数据验证了所建立模型的合理性.该模型可为寒冷地区在役砌体结构的有限元模拟及耐久性评估提供试验及理论支撑.
1 试验概况
1.1 砌体试件
根据GB/T 50129—2011《砌体基本力学性能试验方法标准》及GB 50003—2011《砌体结构设计规范》的规定,制作轴心受压砌体试件.砌体试件尺寸为365mm×240mm×746mm(长×宽×高),砌筑灰缝厚度取10mm.采用砌筑砂浆砌筑砌体试件.
本文研究的是寒冷环境对砌体损伤性能的影响,同时考虑到砌体试件本身具有较大的离散性,需要有大量试验数据并对之进行统计分析才能保证试验结果的准确性.因此,笔者设立了4组(A,B,C,D组)不同冻融循环水平(冻融循环0,40,80,120次)试验,每组试验6个砌体试件.所有砌体试件严格按照GB 50203—2011《砌体工程施工质量验收规范》砌筑完成,施工质量达到B级.
1.2 冻融大气环境模拟
采用人工气候模拟实验室模拟冻融大气环境.该实验室附有先进的智能数字控制系统,可设置温度、湿度、淋水时间、光照时间及冷风等.
冻融循环制度参考ASTM-C 666[5],JGJ/T 70—2009《建筑砂浆基本性能试验方法标准》和GB/T 4111—1997《普通混凝土长期性能和耐久性能试验方法标准》设置.具体冻融循环制度见表1.
砌体试件经28d养护后,从养护室取出并进行外观检查,筛选出表面及灰缝无破损的合格试件.为保证砌体试件在冻融循环试验前处于饱水状态,用自来水喷淋试件12h.将处于饱水状态的砌块试件摆放于人工气候模拟实验室内,试件间距不小于30cm.

表1 冻融循环制度Table 1 Patterns for freeze-thaw cycles
1.3 材性试验
选用陕西建新环保科技发展有限公司生产的(再生)混凝土砖,尺寸为240mm×115mm×53mm(长×宽×厚),强度等级MU15.选用秦岭P·O 32.5R水泥、优质石灰膏、中砂、聚羧酸系高效减水剂配制砌筑砂浆.砌筑砂浆配合比如表2所示.

表2 砌筑砂浆配合比Table 2 Masonry mortar mix proportion kg/m3
将6 块砌筑砂浆试块(尺寸为70.7mm×70.7mm×70.7mm)及6 块混凝土砖置于人工气候模拟实验室,执行1.2节设置的冻融循环制度,然后依据JGJ/T 70—2009和GB/T 2542—2003《砌墙砖试验方法》进行抗压强度测试,取平均值.砌筑砂浆试块及再生混凝土砖抗压强度平均值如表3所示.

表3 砌筑砂浆试块及混凝土砖抗压强度平均值Table 3 Average compressive strength of masonry mortar specimen and concrete brick MPa
1.4 砌体试件轴心受压试验
砌体试件轴心受压试验在YAW-5000 长轴压力机上进行.该压力机最大压力为5 000kN.试验前,沿砌体试件垂直中线和水平中线各布置1个应变百分表,2个应变百分表测点间距为300mm,水平中线上应变百分表测点与试件边缘的距离为50mm(见图1).砌体试件安装就位后,首先对其施加5%的预估极限荷载,检查应变百分表的灵敏程度和安装是否牢固,然后施加5%~20%的预估极限荷载并反复3~5次,调整控制2个宽侧面(长/高侧面)轴向变形的误差不超过10%.试验加载采用逐级加载的方式,每级荷载为预估极限荷载的10%,且在1.0~1.5min内匀速施加完成.恒定荷载1~2min后,施加下一级荷载.当荷载施加至80%的预估极限荷载后,按原定加载速度继续加载,直至试件破坏.记录每个砌体试件初裂荷载(Fcr)、极限荷载(Fu)、应变(ε)及峰值应变(εm),计算每个砌体试件应力(σ)和峰值应力(σm),计算每组砌体试件初裂荷载平均值,极限荷载平均值Fu以及峰值应变平均值.

图1 测点布置Fig.1 Measuring point arrangement
2 试验结果及分析
2.1 砌体轴心抗压强度
实际砌体轴心抗压强度ft按下式计算:

式中:A 为砌体试件的受压截面面积,mm2.
参照GB 50003—2011给出的砌体轴心抗压强度平均值计算公式,根据本文的试验结果,给出了考虑冻融循环作用的砌体轴心抗压强度平均值计算式如下:
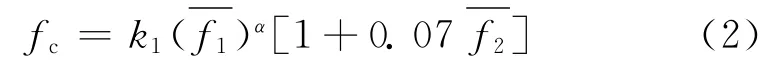
式中:fc为砌体轴心抗压强度计算平均值;分别为混凝土砖及砌筑砂浆抗压强度平均值(见表3);k1为与砌体类别有关的参数;α为与砌体类别及高度有关的参数.
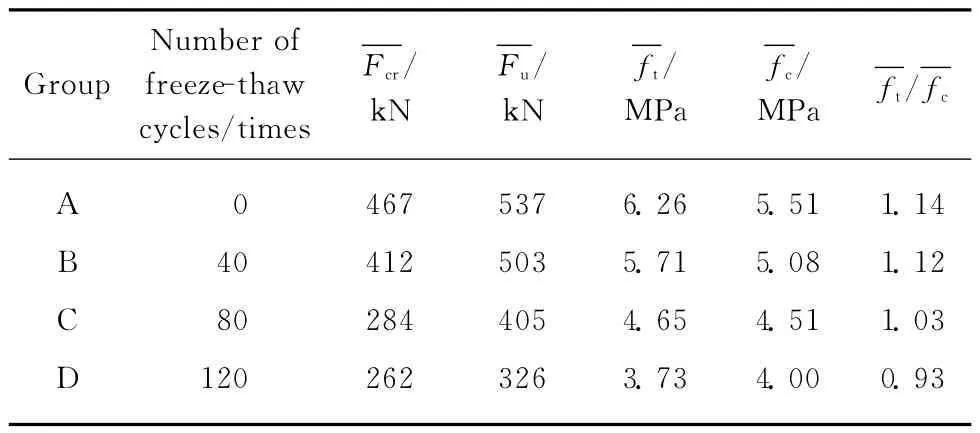
表4 各组砌体轴心抗压强度实测平均值与计算平均值Table 4 Test and calculation average axial compressive strength for each group of masonry
由表4可知,当冻融循环次数达120次时,砌体轴心抗压强度实测平均值降低幅度达40%.
2.2 砌体受压变形性能

表5 砌体弹性模量Table 5 Elastic modulus of masonry
由表5可以看出:随冻融循环次数增加,砌体弹性模量减少.当冻融循环次数达120次时,砌体弹性模量下降幅度高达60%.
本文提出了考虑冻融损伤影响的砌体弹性模量衰减模型:

式中:En为n 次冻融循环后砌体的弹性模量;E0为未冻融砌体的弹性模量;αE为砌体弹性模量衰减系数.依据表5中的试验数据,利用二次函数拟合得到αE=1-0.005 4n.将αE=1-0.005 4n 代入式(3),得:

3 损伤本构关系模型研究
冻融循环和轴心受压均可以通过材料内部微观变化使砌体产生损伤.冻融循环后再进行轴心受压试验的砌体实际上经历了2种损伤过程:经过28d养护的砌体进行冻融循环试验后,等效于第1级加载,达到第1级损伤状态;冻融循环结束后的砌体进行轴心受压试验,相当于第2级加载,达到第2级损伤状态.
3.1 砌体冻融损伤本构关系模型
根据应变等价原理,当材料受到外力作用发生损伤扩展时,任取其中2种损伤状态,则材料在第1种损伤状态下的有效应力作用于第2种损伤状态引起的应变等价于材料在第2种损伤状态下的有效应力作用于第1种损伤状态引起的应变.
本文将砌体试件养护完成后的初始损伤状态看作是第1种损伤状态,经过冻融循环损伤后的状态看作为第2 种损伤状态.利用上述应变等价原理,可得:
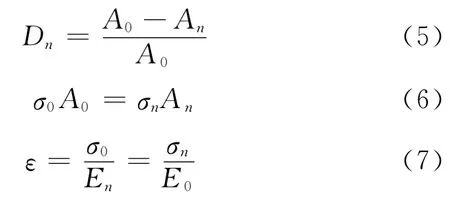
式中:Dn为砌体经历n 次冻融循环后的损伤,即砌体冻融损伤;A0为初始损伤状态下砌体的有效承载面积;An为冻融循环损伤状态下砌体的有效承载面积;σ0为初始损伤状态下砌体的应力;σn为冻融循环损伤状态下砌体的应力.
联立式(5)和式(6),得:

联立式(7)和式(8),得:

式中:εn为冻融循环损伤状态下砌体的应变.式(10)即为砌体冻融损伤本构关系模型.
3.2 冻融损伤演化方程
根据砌体在不同冻融循环后弹性模量的变化,建立其冻融损伤演化方程.与混凝土损伤演化方程类似,在给出砌体冻融损伤演化方程之前,先作如下假设:
(1)在冻融循环试验之前,认为砌体的初始损伤值为0.
(2)砌体冻融损伤只是关于冻融循环次数的函数,不考虑冻融温度不均匀性、孔隙率等其他因素的影响.
(3)随着冻融循环次数的增加,砌体损伤值(正值)逐渐增加.
根据宏观唯象损伤力学的基本理论,砌体冻融损伤Dn定义为:
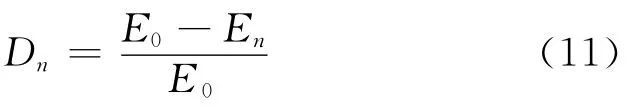
由式(11)计算得到不同冻融循环次数下砌体的冻融损伤值,然后通过数据拟合获得砌体冻融损伤演化方程:

依据式(12)计算出不同冻融循环次数下砌体的冻融损伤值,见表6.
3.3 轴心受压损伤本构模型
在轴心受压过程中,砌体在应力σ 作用下产生宏观应变ε.根据宏观单元体内压力方向的平衡条件,可得:

式中:D 为砌体轴心受压损伤.

表6 不同冻融循环次数下砌体的冻融损伤值Table 6 Damage values of masonry under different numbers of freeze-thaw cycles
式(13)为砌体轴心受压时的损伤本构关系模型,其与经典Mazars单轴弹性损伤本构关系模型[6]相同.
确定了砌体轴心受压损伤演化方程即可确定其轴心受压损伤本构关系的具体表达式.再次利用应变等价原理,把冻融循环后的损伤状态看作第1种损伤状态,冻融循环之后由于进行轴心受压而引起的损伤状态看作第2种损伤状态,由此可得砌体冻融循环后轴心受压损伤本构关系:

将式(9)代入式(14),得到冻融循环后砌体轴心受压应力-应变关系:

式中:Dk=-D-Dn+DDn,即Dk为砌体经历冻融循环和轴心受压之后的损伤.
3.4 轴心受压损伤演化方程
从细观角度对砌体轴心受压破坏机理进行分析.由于对于有限个细观单元体的集合,其材料破坏强度一般服从Weibull统计分布,因而也可以认为材料轴心受压损伤D 服从Weibull统计分布.根据两参数的Weibull统计分布,有:
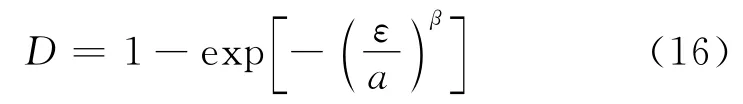
式中:a和β 分别表示尺度参数和形状参数,且均为非负数.
将式(16)代入式(13),得:

由砌体的单轴受压应力-应变关系曲线的基本特征可知,在其达到峰值应力前应符合以下几何条件:
(1)当ε=0时,σ=0;
(2)当ε=0时,dσ/dε=E0;
(3)当ε=εm时,σ=σm;
(4)在峰值应力处,dσ/dε=0.
将式(17)的两边同时对应变ε求导,得:

式(17)和式(18)满足条件(1)和条件(2).
由式(17)和条件(3)得:

对式(19)两边同时取2次自然对数并整理,得:
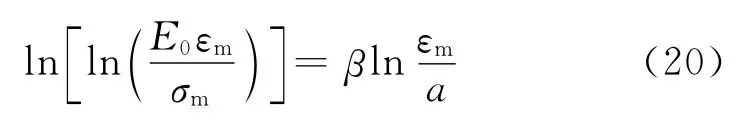
再由式(18)和条件(4)得:

式(21)两边同时取自然对数,得:

将式(20)和(22)联立,求得形状参数β 的表达式:

整理式(21),获得尺度参数a的表达式:

将式(24)代入式(16),得:

式(25)即为砌体轴心受压损伤演化方程.
3.5 冻融循环下轴心受压砌体损伤本构关系模型
将式(11)和式(25)代入方程Dk=-D-Dn+DDn中,得到冻融循环下轴心受压砌体损伤演化方程:

将式(26)代入式(15),得:
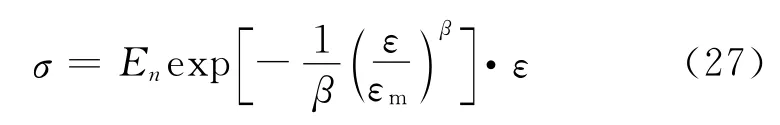
式(27)即为冻融循环下轴心受压砌体损伤本构关系模型.从式(27)可以看出,形状参数β对轴心受压条件下砌体的变形特性起着决定性的作用;冻融循环后轴心受压砌体的应力仅仅与弹性模量E0与En、峰值应变εm和峰值应力σm有关,而上述4个参数均可以通过冻融循环后砌体轴心受压试验得到.
3.6 模型的验证
采用式(27)拟合冻融循环后轴心受压砌体的应力-应变关系曲线,结果如图2所示.
由图2可以看出,式(27)能很好地拟合冻融循环后轴心受压砌体的应力-应变关系.式(27)可为冻融循环下轴心受压砌体结构的耐久性分析提供参考.

图2 冻融循环后轴心受压砌体应力-应变关系拟合曲线Fig.2 Stress-strain fitting curve of the masonry under freeze-thaw cycles and axial compression
还应指出一点,虽然本文推导冻融循环下轴心受压砌体损伤本构模型的过程是基于试验出发,先考虑冻融损伤再考虑轴心受压损伤(砌体轴心受压即损坏),但现实中砌体结构通常是先承受压力再在使用过程中遭受冻融侵蚀.由于目前受试验设备条件的限制,不能同时进行轴心受压和冻融循环试验,然而在建立冻融循环下轴心受压砌体损伤本构关系模型的过程中,是将冻融损伤和轴心受压损伤作为相对独立的损伤状态,所以本文所建立的模型较为合理,可为砌体结构有限元模拟和耐久性分析提供参考.
4 结论
(1)当冻融循环次数达120次时,砌体轴心抗压强度实测平均值降低达40%,弹性模量下降达60%,说明冻融损伤对砌体结构耐久性影响不容忽视.
(2)将冻融循环后轴心受压砌体损伤等效为砌体冻融损伤和轴心受压损伤的非线性耦合,可准确地反映冻融循环下轴心受压砌体的损伤特性.
(3)所建立的冻融循环下轴心受压砌体损伤本构关系模型能较好地拟合冻融循环后轴心受压砌体的应力-应变关系,可应用于寒冷地区在役砌体结构的有限元模拟和耐久性分析.
[1]ROSENHAUPT S,SOKAL Y.Masonry walls on continuous beams[J].Journal of the Structural Division,ASCE,1965,91(1):155-171.
[2]YETTRAM A L,HIRST M J S.An elastic analysis for the composite action of walls supported on simple beams[J].Building Science,1971(6):151-159.
[3]SAW C B.Linear elastic finite element analysis of masonry walls on beams[J].Building Science,1974(9):299-307.
[4]施楚贤.砌体结构理论与设计[M].3版.北京:中国建筑工业出版社,2003:36-37.SHI Chuxian.Masonry structure theory and design[M].3rd ed.Beijing:China Architecture &Building Press,2003:36-37.
[5]ASTM-C 666 Standard test methods for sampling and testing brick and structural clay tile[S].
[6]BAQI A,BHANDARI N M,TRIKHA D N.Experimental study of prestressed masonry flexural elements[J].Journal of Structural Engineering,ASCE,1999,125(3):245-254.

