基于排列熵和CHMM 的齿轮故障诊断
丛 华,崔 超,刘远宏,冯辅周
(装甲兵工程学院,北京 100072)
0 引言
齿轮箱作为重要的传动部件,被广泛应用于各类机械设备中,对其进行故障诊断与分类研究具有重要的实际意义[1]。振动信号是齿轮箱故障特征信息的有效载体,对振动信号的分析可实现不停机操作下的齿轮箱故障诊断。但振动信号特别容易受到噪声干扰,特别是对复杂设备,众多运动部件同时产生振动激励,使得实际获取信号的信噪比不高[2],而目前信号主要的时频分析方法有短时傅里叶变换、Wigner-Ville 分布、小波尺度分析等,这些方法的时频分辨率都受到不确定性原理的限制,因此无法同时在时域和频域得到很好的分辨率。故障识别模型以神经网络模型应用最广,但运用中需要大量的训练样本,在训练样本有限的条件下,泛化能力较差;隐马尔可夫模型(HMM)具有很强的特征分类能力,最早应用于语音识别领域[3],它所具有的两层随机结构与基于振动的故障诊断机理较为接近,但目前的研究多用于离散观察序列,对于连续信号,需要首先进行离散化处理。
排列熵反映了一维时间序列复杂度,用于信号特征提取可以很好地放大系统的弱变信号,同时检测出复杂系统的动力学突变;CHMM 的输出序列不存在量化处理,能够比较精确地表示原始信号,有利于提高识别精度。结合两种模型的优点,提出一种基于排列熵和连续隐马尔可夫(CHMM)的齿轮故障特诊断方法,并通过试验验证该方法的有效性。
1 CHMM 建模
首先介绍隐马尔可夫(HMM)模型。HMM 是一种统计分析模型,用来描述一个含有隐含未知参数的马尔可夫过程,其研究对象是一个数据序列[4]。模型可记为:λ=(N,M,π,A,B),或简写为:λ=(π,A,B)。其中:N 为模型中Markov 链的状态数;M 为每个状态对应的可能观测值数;π为初始状态概率分布矢量;A 为状态转移概率矩阵;B 为观测值概率矩阵。
连续隐马尔可夫模型(CHMM)是HMM 的一种改进算法。所谓CHMM,是指观测值为一个连续随机变量,任一状态对应的观测值的观测概率由一个观测概率密度函数表示,该密度函数可以通过高斯概率密度函数模拟产生。在实际应用中,常常用几个高斯概率密度函数的线性组合模拟观测序列的产生。如果高斯概率密度函数足够多,则混合高斯密度可以逼近任意的概率分布函数[5]。每个高斯概率密度函数都有各自的均值和协方差矩阵,这些参数可以通过大量的观测样本特征统计得到。记观测概率密度函数为b j(o)。

式中:o 表示观测向量D ×T(D 为维数,T 为观测序列长度);M 为每个状态包含的混合高斯元个数;cjl表示第j 个状态第l 个混合高斯元的权值(即混合系数);G 表示正态高斯概率密度函数;μjl表示第j 个状态第l 个混合高斯元的均值矢量;Ujl表示第j 个状态第l 个混合高斯元的协方差矩阵。一个具有混合密度形式的CHMM 可以用五元组来表示:

机械系统的振动观测序列通常都是连续变化的信号,尽管可以通过标量量化将一个特征矢量信号进行离散并符号化,但有可能降低信号所包含的信息特征。而CHMM 直接以特征矢量作为观测序列,可最大限度地保留信号的特征信息,因此采用CHMM 进行故障预测可以获得更高的精度。
2 排列熵算法
设一离散时间序列{x(i),i=1,2,3,…,n},对其中任意元素进行相空间重构[6],得到

式中,m、τ 分别为嵌入维数和延迟时间。将x(i)中的m 个重构分量{x(i),x(i +τ),…,x(i +(m-τ)}按照升序重新排列,即

如果重构分量中存在相等的值,即
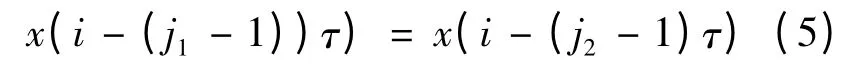
按照j1,j2值的大小来排序,也就是j1<j2当时,有

因此,对于任意一个时间序列重构所得的矩阵Y 中每一行Y(j)都可以得到一组符号序列:

其中,l=1,2,…,k,且k≤m!,m 维相空间映射不同的符号序列(j1,j2…,jm)总共有m!,符号序列S(l)是其中的一种排列[7]。计算每一种符号序列出现的概率p1,p2…,pk,此时,时间序列X(i)的k种不同符号序列的排列熵可以按照Shannon 熵的形式定义为:

当Pj=1/m!时,Hp(m)就达到最大值ln(m!)。为了方便,通常用ln(m!)将Hp(m)进行归一化处理,即

3 故障诊断试验
3.1 试验装置
试验在自主搭建的变速箱系统试验台上进行。试验台主要包括变速箱、转速控制台、三相异步电动机、电磁测功仪、扭矩测试仪、功率控制仪、传感器和采集设备等。变速箱为某型坦克变速箱,功率输入由转速为1 200 r/min、额定功率为5 kW的交流异步电动机驱动,转速由转速控制台调节,在终端连接一吸收功率为45 kW 的电磁测功仪,起到负载的作用(图1)。信号采集通过基于虚拟仪器平台搭建的数据采集系统完成。
试验中变速箱挂Ⅲ档,主动齿轮齿数为14,从动齿轮齿数为27,预加载的扭力为100 N·m。对正常、轻微磨损、严重磨损、断齿4 种状态进行试验。在被动齿轮某齿齿面上,利用磨床在齿面上磨掉少许深度,模拟轻微磨损故障,磨损深度1~2 mm,模拟严重磨损故障,在某齿的齿端处,通过铣床铣掉一个齿,模拟断齿故障(图2)。

图1 试验装置Fig.1 Experimental facilities

图2 齿轮故障Fig.2 Failed gear
3.2 数据预处理和特征提取
试验中传感器选用DYTRAN 公司生产的3215M1 型单自由度加速度传感器,测点布置在靠近输出轴端的箱体表面外侧,该测点距离振源较近,能够较好地获取档位齿轮故障位置附近的振动信号。采用编码器控制采集,使每次采集的相位都一致,采样频率为20 kHz,数据采集宽度为10 s,每种状态采集5 个数据样本,每个样本文件含有20 万个采样点。图3 所示为每组第一个样本的振动情况。可以看出,齿轮存在磨损和断齿时信号的振幅明显高于正常状态,并且存在周期性冲击的信号。根据参数计算得到故障齿轮的啮合频率为233.5 Hz。
原始信号含有大量的噪声,致使有用信息淹没在噪声里,所以首要进行降噪处理。采用小波相关滤波法进行降噪,该算法是利用各层信号之间的相关特征将信号中的重要特征信息与噪声区分开,从噪声中检出重要的信号边缘,并移除噪声,使得信噪比大大提高[4,8]。
采用前面介绍的排列熵算法对降噪信号进行分析,嵌入维数m=4,延迟时间τ=1(试验发现m 取4~6,τ 取1~3,结果差异无显著意义)。将样本数据10 万个点每200 个点为一组,共分为400 个组,计算的排列熵变化情况如图4 所示。
排列熵反映了一维时间序列复杂度,在这里运用排列熵可以反映齿轮振动信号的复杂度。在转速、负载相同的情况下,齿轮振动信号的排列熵越大,振动信号越随机;反之,排列熵越小,振动越平稳。当齿轮发生磨损或断齿时,机械设备发生异常必然产生异常频率成分,由于有缺陷的齿轮在啮合过程中存在的低频、低振幅所激发的高频、高振幅共振,排列熵值能够有效反映这些突变信号特征。计算得到各样本的排列熵参数如表1所示。
3.3 CHMM 建模
由于CHMM 的初始概率π 和状态转移矩阵A 的初始值选取对模型的训练结果影响不大,这里采用等概率方式产生[9],即各模型初始状态转移矩阵和初始观测值概率矩阵分别为


图3 原始振动信号Fig.3 Vibration signals of the gear

图4 降噪信号排列熵Fig.4 Permutation entropy of the noise reduction signals

表1 样本排列熵参数Table 1 Permutation entropy parameter of the examples

续表1
而CHMM 中观测值概率矩阵的初值对模型的训练结果影响较大,并且需要考虑不同样本对输出结果的影响,这就涉及到CHMM训练的问题,即混合高斯概率密度函数中的均值、方差和权系数应该如何初始化的问题[10]。采用的方法是:将几个属于同一观察样本的特征矢量组成一个大的矩阵(试验中将每个状态的前3 个样本组成一个大的观察序列),然后对这个矩阵进行分段,对每一段的特征矢量进行K-调和均值聚类,得到连续混合高斯概率密度函数。从理论上讲,使用混合高斯元个数越多,拟合模型的精度越高,然而计算速度会变得越慢[11]。考虑到这一问题,在CHMM 的建模过程中,对每段特征矢量,选取4个高斯元来构建连续混合高斯概率密度函数,每个状态模型的状态数取为4。按照上述方法可对正常状态下观测值概率矩阵的混合高斯概率密度函数中的均值矩阵M、协方差矩阵C 和权系数矩阵W 进行如下形式的初始化(其他状态类似):


图5 给出了4 种状态下模型的训练曲线,最大迭代次数为50,4 种模型的对数似然概率随着迭代次数的增大而增大,在20 步内均达到收敛。
3.4 试验结果分析
各种状态的模型建立以后,用各组数据的后2 个样本诊断故障,验证模型的准确性,模拟试验的测试统计结果见表2。表中数值为最大对数似然概率值,数值越大,表示越接近模拟的状态,从表2 中可以看出,算法对每种故障的诊断结果较为理想。在实际诊断中,可以通过多次采集数据进行训练,进一步提高故障诊断的精度。

表2 故障诊断试验结果Table 2 Results of fault diagnosis experiment

图5 CHMM 训练图Fig.5 Training diagram of CHMM
4 结论
1)以齿轮振动信号为研究对象,运用小波相关法进行降噪,并利用排列熵算法较好地提取了目标齿轮的信号特征。
2)应用CHMM 进行齿轮的故障诊断,减少了对连续观察序列进行离散化处理这一步骤,提高了诊断精度,并通过齿轮箱试验系统验证该方法的有效性。
[1]丁康,李巍华,朱小勇.齿轮及齿轮箱故障诊断使用技术[M].北京:机械工业出版社,2005:10-26.
[2]李斌,郭瑜,刘亭伟,等.基于独立分量分析与包络阶比分析的齿轮箱多振源特征提取[J].振动与冲击,2012,31(19):68-72.
[3]国立新,莫福源,李昌立.基于连续高斯混合密度HMM 的汉语全音节语音识别研究[J].声学学报,1995,20(5):321-329.
[4]陆汝华,王鲁达.基于状态加权合成的HMM 滚动轴承故障诊断[J].轴承,2011(10):53-56.
[5]王国峰,李玉波,秦旭达,等.基于TVAR-HMM 的滚动轴承故障诊断[J].天津大学学报,2010,43(2):168-173.
[6]印欣运,何永勇,彭志科,等.小波熵及其在状态趋势分析中的应用[J].振动工程学报,2004,17(2):165-169.
[7]冯辅周,司爱辉,饶国强,等.基于小波相关排列熵的轴承早期故障诊断技术[J].机械工程学报,2012,29(3):73-79.
[8]王文欢,王细洋,万在红.基于细化谱和隐马尔可夫模型的齿轮故障分类方法[J].失效分析与预防,2014,9(1):30-34.
[9]Atlas L,Ostendorf M,Bernard G D.Hidden Markov models for monitoring machining tool-wear [C].IEEE International Conference on Acoustics,Speech and Signal Processing,2000:3887-3890.
[10]Liu B,Riemenschneider S,Xu Y.Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum[J].Mechanical Systems and Signal Processing,2006,20(3):718-734.
[11]Hilton M L,Ogden R T.Data analytic wavelet threshold selection in 2-D signal denoising[J].IEEE Transaction on Signal Processing,1997,45(2):496-500.

