湘江长沙综合枢纽隔板型式鱼道三维水流数值分析

彭 鑫

（长沙市湘江综合枢纽开发有限责任公司 长沙市 410200）

前言

随着我国经济的发展，国家对生态保护日益重视，水利建设也已开始从传统水利向资源水利转变，保护水生态环境、实现人与自然的和谐共处已得到社会的普遍共识。鱼道作为湘江长沙综合枢纽的重要组成部分，承担着沟通鱼类洄游通道、保障湘江流域水生态环境的重任，鱼道水力设计的好坏直接影响到鱼类能否顺利通过大坝。因此，开展鱼道水流条件研究具有十分重要的意义[1]。

传统的物理模型试验受试验技术的限制，对鱼道池室水流条件的研究只能进行定性的观察。近些年来，随着计算机软、硬件、理论研究以及数学计算方法的迅猛发展，数值模拟成为研究中日益重要的手段。和物理模型相比，数学模型更具备灵活性、快捷、高效，且费用较低。这些优点都决定了数值研究不断走向深入并且成为解决工程实际问题的主要手段。汪红波[2]、郭维东[3]、王球[4]等学者均运用数值模拟技术很好地解决了鱼道工程中的水力学问题。考虑到鱼道内水流条件复杂，呈现明显的三维水流特性。因此本文运用三维数值模拟技术，对隔板型鱼道水流条件进行计算分析。

1 数学模型的建立

1.1 基本方程

基于不可压缩水流条件，采用双方程紊流模型，数学模型基本控制方程为：

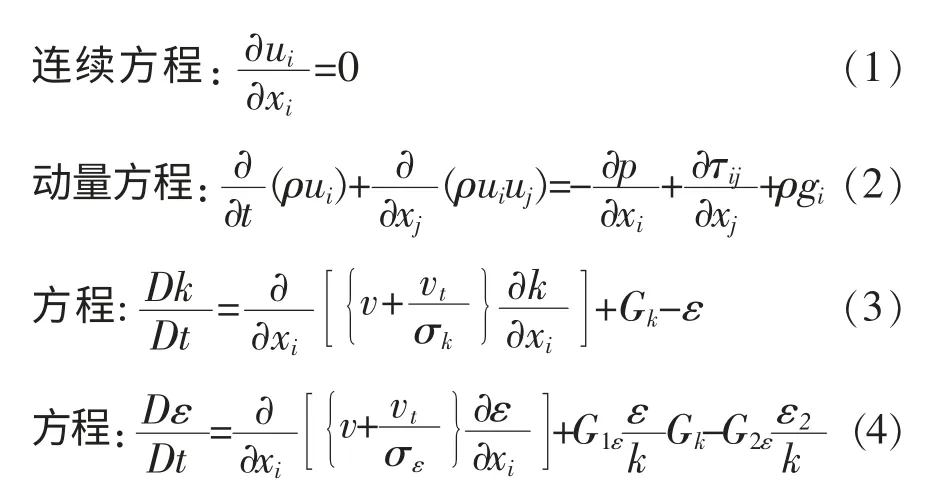
其中，t 为时间；ui和xi分别为速度分量和坐标分量；v 为运动粘性系数；ρ 为修正压力；τij为应力张量，定义；ρgi为重力体积力；μt=ρvt=pcuk2/ε 为紊动动力粘性系数；δij为Kronecker delta 符号。式中的经验常数取值为cu=0.09，σk=1.0，σε=1.33，C1ε=1.44，C2ε=1.42；Ck为 平均速度梯度引起的紊动能产生项，Ck=vt

自由表面采用VOF（The Volume of Fluid）方法。在空间上定义函数F，全含水为1，不含水为0。当为自由表面时，0＜F＜1。函数F 是空间和时间的函数，即F=F（x,y,z,t），可以理解为固结在流体质点上并随流体一起运动的没有质量和粘性的染色点的运动，其输运方程为：

1.2 数值计算方法

将式（4）～（8）写成如下的通用形式：

式中 t——时间矢量；

uj——为和速度矢量；

Ф——通用变量，如速度、紊动能等；

ГФ——变量Ф 的扩散系数；

SФ——方程的源项。

计算时，首先对式（6）在任意控制体积CV（其边界为A）作体积分，利用高斯定理将体积分化成面积分。记（Ф）=pФu-ГФgradФ，可得到有限体积法的基本方程，写成：

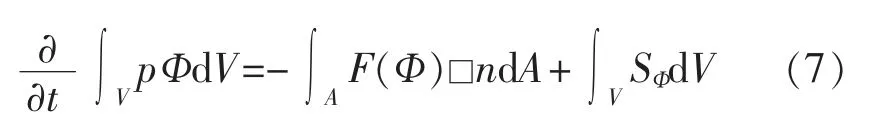
式中 F（Ф）□n——法向数值通量。

对控制体积单元取平均后，可离散得到有限体积法的基本方程的最终形式为：

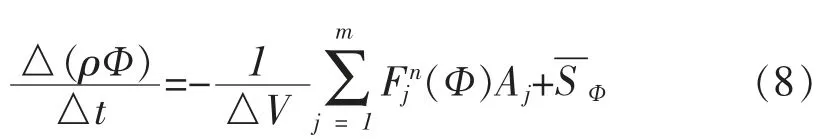
式中 △V——单元体积；

M——单元面总数；

Aj——单元面j 的面积；

1.3 定解条件

上游进口和下游出口计算边界分别采用自由面水位作为其边界条件；壁面采用Launder 和Spalding的壁面函数条件，进出口的紊动能k 和耗散率ε 由下列经验公式得出：

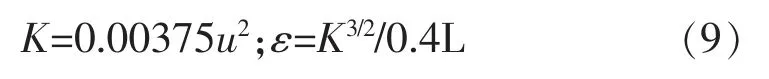
式中 L——紊流特征长度。

1.4 计算区域

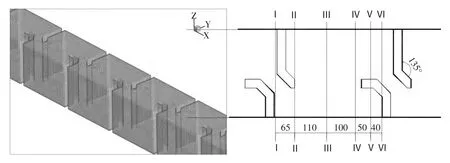
图1 鱼道三维水流计算网格划分及典型池室断面定义

如图1 所示，数学模型计算区域包括5 块隔板，鱼道槽身计算长度总长27.0 m，由于隔板型式较为复杂，计算区域采用四面体进行网格划分。为便于分析，将池室断面进行定义。

2 结果分析

图2 分别给出鱼道池室沿程流态及流速分布。数值模拟计算结果表明距离鱼道池室底部0.5 m 高程平面，沿程2#～7#隔板过鱼孔断面最大流速约为（1.03～0.93）m/s；在距离鱼道池室底部1.5 m 高程平面，沿程2#～7#隔板过鱼孔断面最大流速约为（0.92～0.94）m/s 左右。根据不同高程过鱼孔最大流速计算数值看，隔板孔口最大流速为1.01 m/s，平均流速为0.91 m/s。从过鱼孔沿程垂向最大流速变化看，过鱼孔底部流速沿程略有减小，过鱼孔中部位置最大流速沿程分布基本较为均匀，过鱼孔上部位置最大流速沿程则略有增加。上级鱼池水流通过竖缝进入下级鱼池时受隔板下游横向导板作用，竖缝流出的水流偏向池室右侧，碰撞右侧池室壁后受下级隔板竖缝导板影响在池室中心部偏下位置（约2.5 m～3.0 m）绕下级竖缝导板流入下级竖缝，主流在上下级池室内形成“S”形流态，并在主流左侧形成流速小于0.2 m/s 的回流区，池室内主流流向明确，但水流主流受竖缝导板作用影响扭曲较为明显。

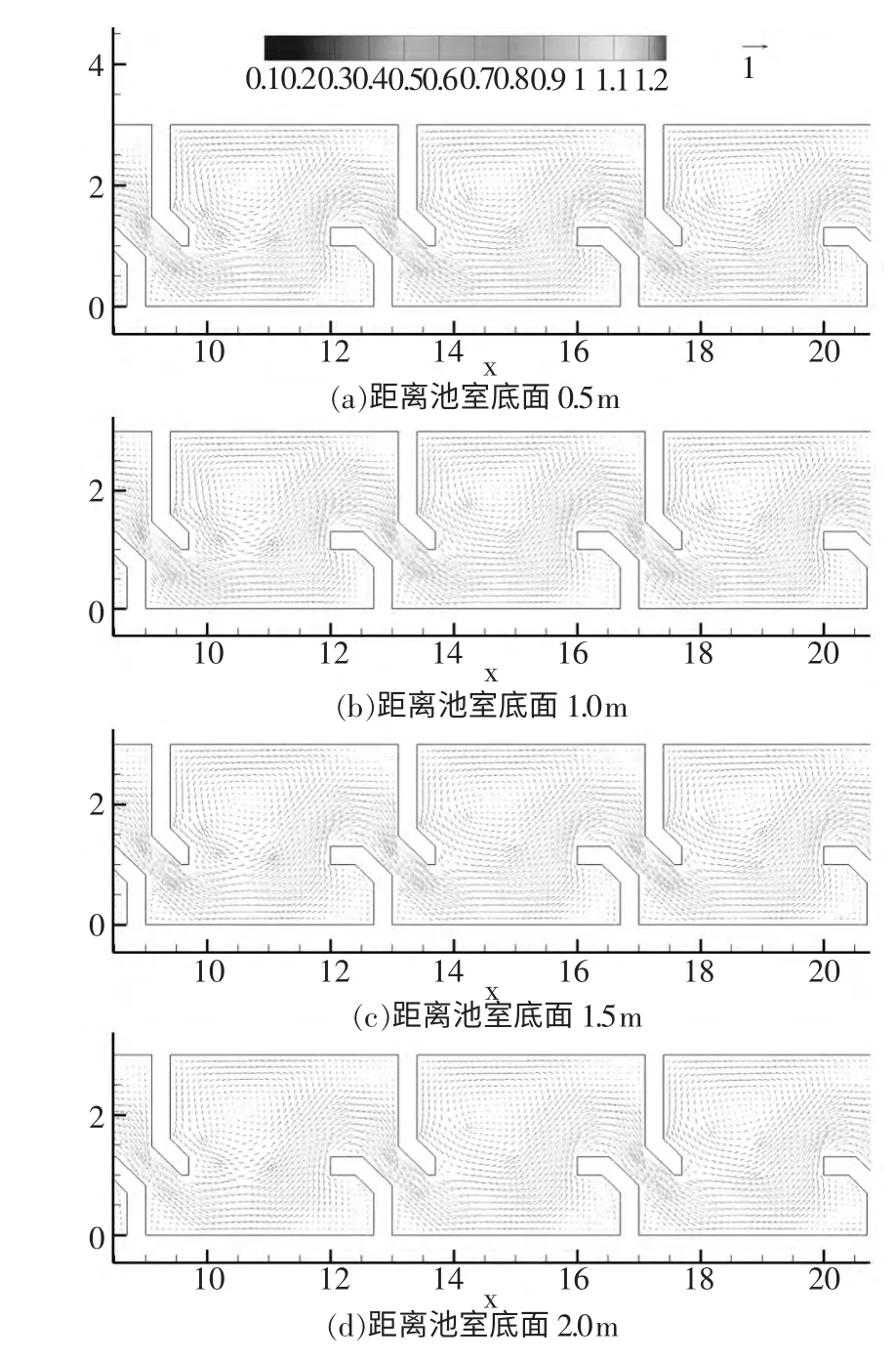
图2 鱼道池室不同高程流态及流速分布数值模拟结果

图3 分别给出鱼道中部第4个池室内不同高程池室内流速分布数值模拟结果。图4～图7 分别给出第4 池室内距离池室底部1.5 m 处不同断面三维流速分布情况，其中坐标原点为鱼池右岸，坐标3 m 为鱼池左岸。可以看出鱼道池室内存在两个流速相对较大的区域，即过鱼孔附近的断面和过鱼孔上游隔板导流翼缘的IV-IV 断面附近。过鱼孔I-I 断面最大流速为0.93 m/s，在IV-IV 断面附近最大流速为0.74 m/s，其余区域流速基本小于0.6 m/s。

由图5 池室内各断面X 向流速分布看，池室内从II-II 断面至V-V 断面出现了回流区，在III-III断面附近最大流速达到0.33 m/s，回流区宽度大约有1.0 m 左右，约占闸室宽度的1/3。由图6 池室内各断面Y 向流速分布可见，池室内在I-I 断面和IV-IV 断面均出现了较大的横向流速，对应相同断面的X 向流速，在IV-IV 断面出现了明显的横向水流，最大横向流速达到0.66 m/s；由Y 向流速分布图还可见，在池室内III-III 断面至V-V 断面间水流主要偏向左侧，其余范围内水流偏向右侧。从图7 可得鱼道池室内各断面Z 向流速值均较小，除过鱼孔I-I断面附近由于水流收缩最大有约0.11 m/s 的垂向流速外，其余区域垂向流速最大仅0.05 m/s，因此在可以忽略鱼道池室内垂向流速的影响。

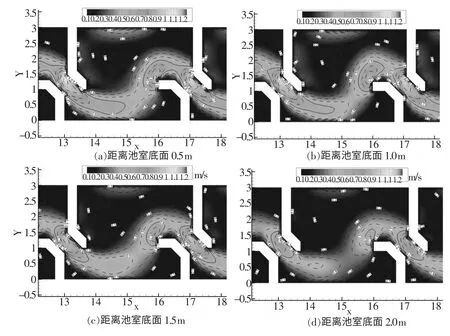
图3 鱼道池室不同高程流速分布

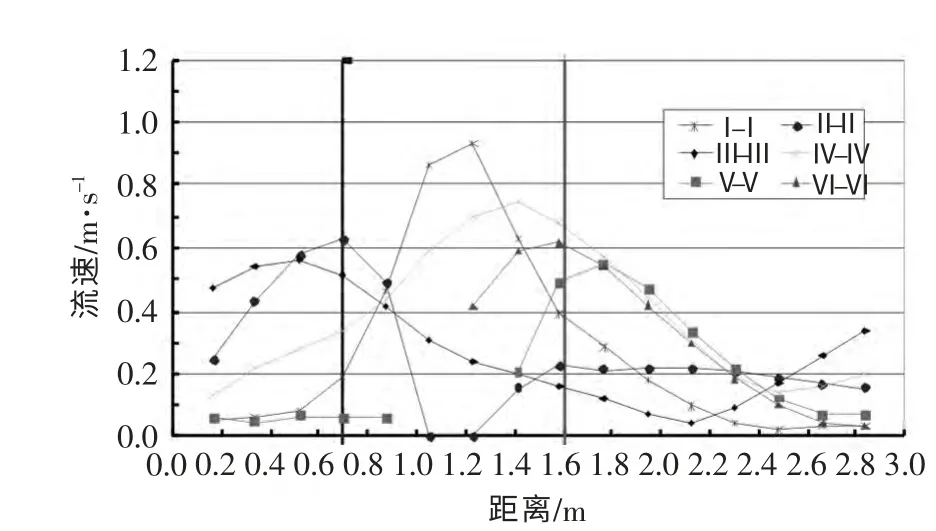
图4 池室内不同断面绝对流速值分布

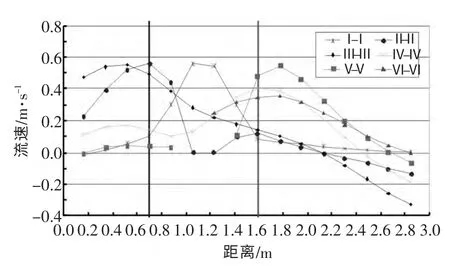
图5 池室内不同断面X 方向流速分布

图6 池室内不同断面Y 方向流速分布

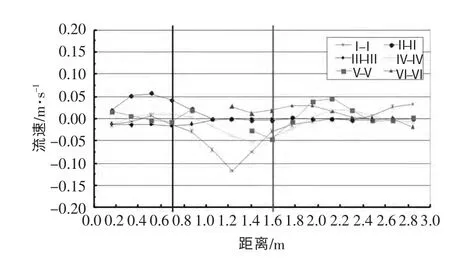
图7 池室内不同断面Z 方向流速分布

根据鱼道池室内三维流态计算结果，鱼道池室内最大流速约为（0.92～1.03）m/s，数模计算的鱼道最大流量为1.21 m3/s，根据公式计算综合流速系数约为0.857，孔口平均流速为0.91 m/s。

3 结论

基于N-S 方程，采用k-ε 双方程紊流模型，建立三维水流数学模型。利用数学模型开展湘江长沙综合枢纽隔板型式鱼道三维水流条件计算分析，分析其三维水流结构，得到鱼道池室内最大流速、最大流量、综合流速系数、以及隔板孔口最大流速和平均流速等重要信息，为鱼道的布置和优化提供科学依据。

[1]李强.长沙综合枢纽工程鱼道布置浅析[J].湖南水利水电，2012，（2）：13-16.

[2]汪红波，王从锋，刘德富，等.横隔板式鱼道水力特性数值模拟研究[J].水电能源科学，2012，30（5）：65-68.

[3]郭维东，赖倩，王丽，等.同侧竖缝式鱼道水力特性数值模拟[J].水电能源科学，2013，31（5）：71-80.

[4]王球，杨文俊，陈辉.竖缝与堰组合式鱼道水力特性数值模拟研究[J].人民长江，2013，44（11）：81-84.