基于平面线圈的基波脉振磁场构造方法研究*

黄 奔彭东林武 亮张天恒

（重庆理工大学机械检测技术与装备教育部工程研究中心，时栅传感器及先进检测技术重庆市重点实验室，重庆400054）

基于平面线圈的基波脉振磁场构造方法研究*

黄 奔，彭东林*，武 亮，张天恒

（重庆理工大学机械检测技术与装备教育部工程研究中心，时栅传感器及先进检测技术重庆市重点实验室，重庆400054）

为了减小电磁式时栅位移传感器的原始误差，提出了一种基于平面线圈的基波脉振磁场构造方法。通过研究现有电磁式时栅磁场构造方法和平面线圈磁场分布特性，利用各次谐波畸变率THD（Total Harmonic Distortion）最小的优化算法，得到平面线圈最优化布置参数，并且在数值分析和有限元分析软件中得到了验证。根据这些参数设置，设计了基于多匝方形平面线圈的新型电磁式时栅位移传感器。在150 mm量程内，新型时栅原始误差为-32 μm～23 μm，较现有电磁式时栅位移传感器减小了42.3%。

基波脉振磁场；平面线圈；谐波畸变率；电磁式时栅；

时栅位移传感器采用时钟脉冲作为空间位移测量基准［］，并将位移测量转换为时间测量，即“以时间测空间”。只需要普通的机械加工精度，就可以获得较高的测量精度。相较于传统的栅式位移传感器，其具有结构简单，成本较低，机械加工性能好，抗干扰能力强等特点，已经应用于精密转台控制系统中［2-5］。然而，现有的电磁式时栅位移传感器的敏感元件是通过在导磁骨架上绕制多匝线圈的方式产生测量所需的磁场分布。这种方法产生的脉振磁场分布函数中含有很多谐波成分，会引起较大的测量误差。实际工程应用中为了减小测量误差，多采用补偿手段，如正弦绕组法，斜槽法等，但这些手段的复杂性制约了时栅位移测量精度的进一步提高。

针对平面线圈的研究，其中清华大学学者描述了平面线圈的自感和阻抗变化，为基于平面线圈的电涡流式传感器设计提供依据和指导［6］；上海交通大学学者将平面线圈用于磁悬浮转子微陀螺，对平面线圈的磁场力进行了仿真模拟［7］；Q.Ramadan等发现在不同形状的平面线圈中密集螺绕线圈产生磁场效率最高［8］；Fava等针对任意旋向的方形螺旋平面线圈建立了二阶阻抗矢量模型［9］。

根据目前电磁式时栅位移传感器中存在的问题，本文提出一种利用平面线圈构造实际测量中所需的基波脉振磁场［10］的方案。将该方案应用于电磁式时栅位移传感器的设计中，进而从设计源头上就减小传感器原始误差，最终提高传感器的测量精度。

1 电磁式时栅脉振磁场

电磁式时栅位移传感器中的旋转磁场［11］是由多相激励信号产生的脉振磁场叠加而成。将两相激励信号的电磁式时栅的定、转子展开成直线并截取其中一部分，如图1所示。激励绕组由正弦绕组和余弦绕组组成，向两相激励绕组中分别通入激励信号sin(ωt)和cos(ωt)时，在定子上方分别产生的磁感应强度Bsin和Bcos，如图2所示。对于单相激励的磁感应强度沿X方向呈现类方波变化，且两相激励信号分别产生周期性分布的脉振磁场相差1/4个节距W。

图1 定转子绕组示意图

图2 两相激励磁感应强度

两相激励电信号在定子上方产生的磁感应强度可表示为式（1）和式（2）

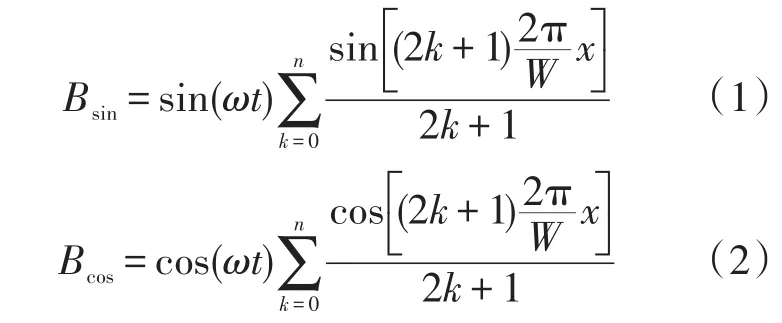
其中，ω为激励信号的频率，k为磁感应强度的谐波次数。

将基波叠加，则得到定子上方总的磁感应强度为

式中，i为整数且大于0，A为常数

根据法拉第电磁感应定律知，电磁式时栅传感器中感应电动势E，如式（4）所示，由于除基波磁场外，还存在一系列高频次谐波磁场，使得感应电动势E相位发生偏移，在实际测量中给传感器带来测量误差。

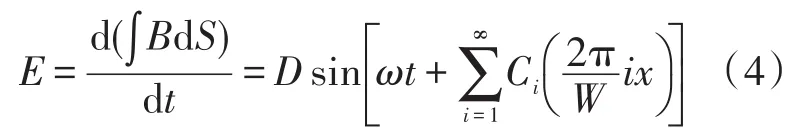
式中，D为常数

因此，若是可以构建测量所需的基波脉振磁场，并有效地控制脉振磁场各次谐波成分，则从设计源头上可以减少测量误差。

2 基于平面线圈的基波脉振磁场构造方法

2.1 平面线圈结构设计

如何用平面线圈构造基波脉振磁场分布，研究者联想到与其形状相类似的古埃及金字塔。金字塔平行于地平面的截面都为正方形，随着高度的升高，正方形的面积在缩小。将金字塔每一层的外轮廓在地平面上投影，就会出现大正方形套小正方形的形式，由此联想到多匝方形平面线圈。单匝方形平面线圈内部产生的磁感应强度近似于匀强磁场，且磁感应强度与线圈匝数、通电电流有关。若在平面上采用匝数相同、通电电流相同，但尺寸逐渐缩小的方形线圈组成多匝方形线圈组，那么在平面上方产生的磁感应强度将是各个线圈产生的磁感应强度相叠加的形式，空间磁感应强度分布类似于“金字塔”形状。

如果在任一时刻任意相邻两方形线圈组电流方向相反，如图3（a）所示，那么就会在平面上方产生类似于三维空间驻波变化形式的磁场，即测量所需的基波脉振磁场。由于平面线圈产生的磁场分布只有沿Z轴方向的磁场分量作用于感应线圈。因此，仅考虑沿Z轴的磁感应强度分量Bz。沿X轴方向磁感应强度Bz变化类似于正弦函数，如图3（b）所示。通过研究平面线圈各参数与磁感应强度分布之间的关系，可使磁感应强度无限变化接近于正弦函数，从而得到基波脉振磁场，三维空间中磁场感应强度，如图3（c）所示。

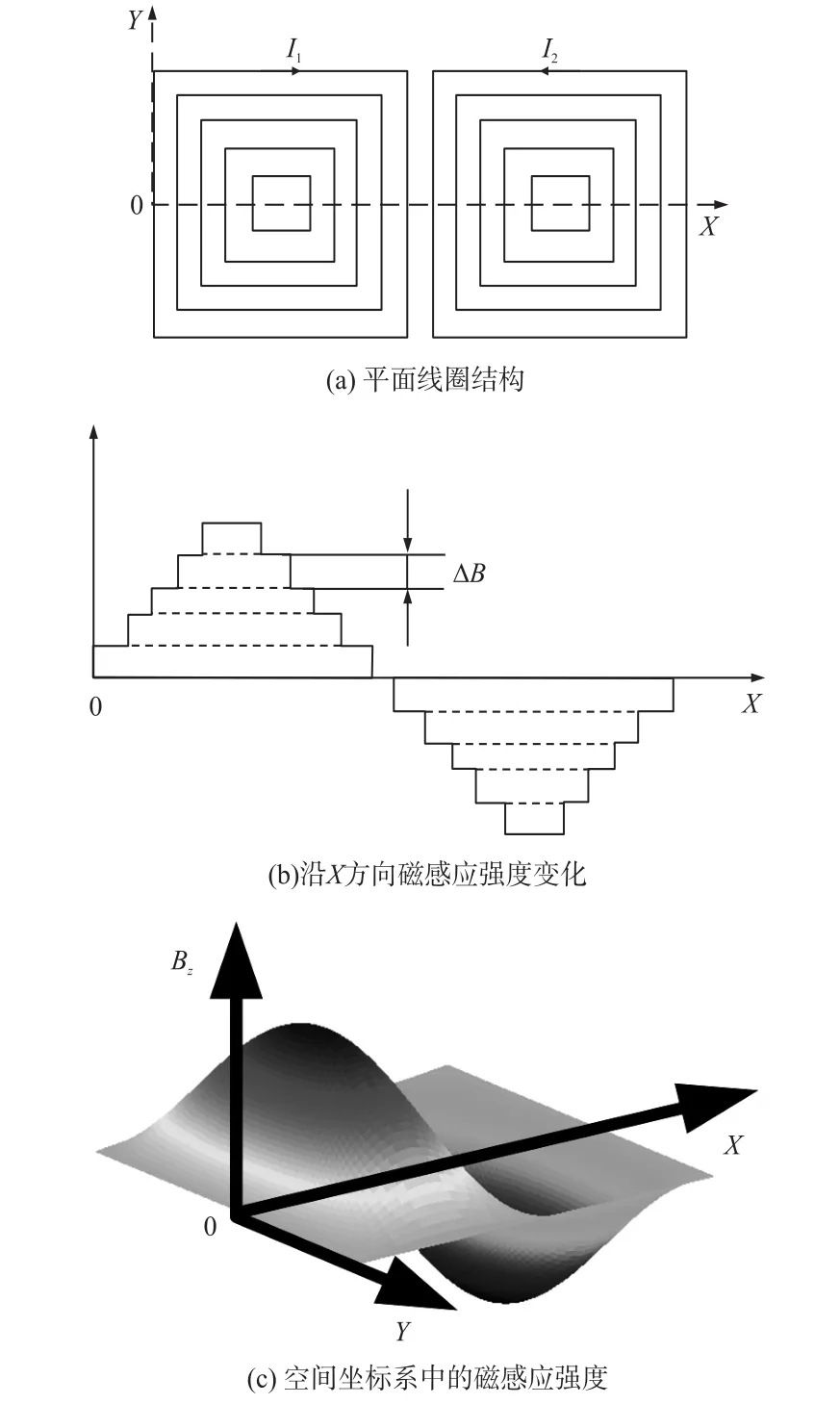
图3 平面线圈及产生的磁场强度示意图

2.2 多匝方形线圈脉振磁场数学模型

根据毕奥-萨伐尔定律，得到单匝方形线圈磁感应强分布函数［12］。由于多匝方形线圈产生的磁场分布可以简化为多个不同尺寸的单匝线圈所产生磁场分布的叠加［7］，多匝方形线圈的结构形状如图4所示。

图4 多匝方形平面线圈

空间内任意点P的磁感应强度可表示

式中，r1=ai+x，r2=ai-x，r3=ai+y，r4=ai-y，BZ为多匝方形线圈的磁感应强度，Bzi为第i匝线圈的磁感应强度，n为平面线圈的总匝数

采用两个多匝方形平面线圈构造测量所需的基波脉振磁场分布，其结构如图5所示。

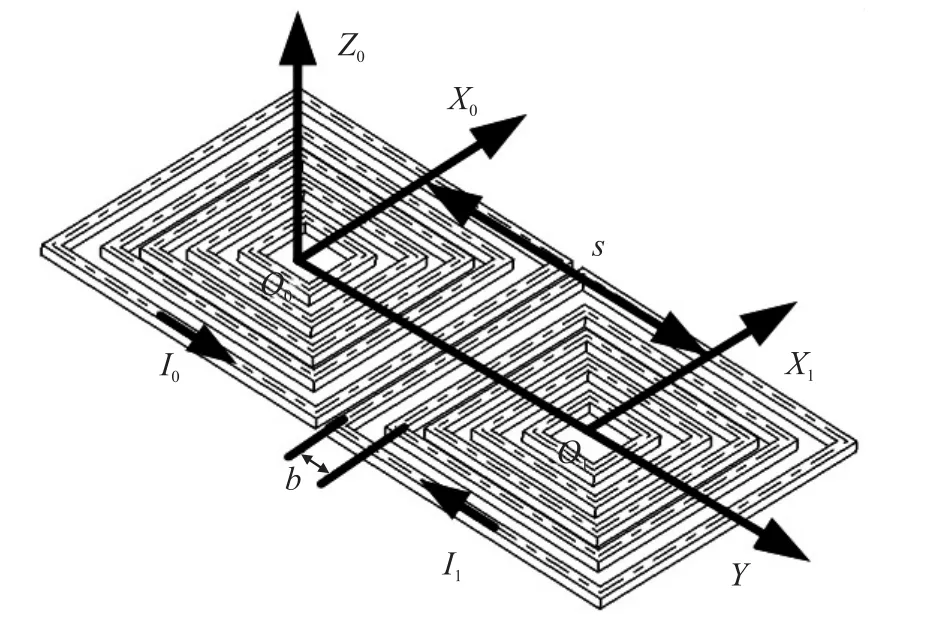
图5 平面线圈结构图

根据坐标变换的原理，构建由平面线圈的坐标系，以初始线圈中心为坐标原点，建立初始坐标系X0O0Y0，再依次将右边线圈中心定为X1O1Y1，如图5所示，其换算关系满足表达式（6）。

其中，s表示两组线圈的中心距，b表示线距，I0与I1大小相同方向相反。

两个平面线圈的Z轴方向磁场分布为两个线圈磁场分布相互叠加，即所构造平面线圈的磁感应强度为

式中，Bz0为初始线圈的磁感应强度，Bz1为相邻线圈的磁感应强度

2.3 平面线圈最优参数布置

测量所需的基波脉振磁场变化形式为正弦形，所以需要对平面线圈的参数进行优化。分析平面线圈的各项参数，当y=0时，磁感应强度Bz随x的变化。设置目标函数为B（a1，a2，a3，…，an，s，x），当目标函数理想波形应无限接近正弦波形时，得到最优参数。取n=5，bmin=200 μm，其最外圈线圈的边长为2.5 mm，即a5=1.25 mm，目标函数的约束条件为

其中ai为第i匝线圈边长的一半，n为匝数。

当目标函数B（a1，a2，a3，a4，a5，s，x）的变化不为理想的正弦形状时，说明其中包含其他的谐波成分，或者说波形发生了畸变［13-15］。采用各次谐波畸变率THD（Total Harmonic Distortion）表示偏离正弦波形的程度，它等于各次谐波的有效值的平方和的平方根与基波有效值的百分比。

式中，Ai表示i次谐波的幅值

当畸变率THD最小时，说明目标函数B（a1，a2，a3，…，an，s，x）的变化最接近正弦形变化，即可得到最优的一组参数。

利用数值分析软件，通过优化算法得到最优参数布置。

①根据a1，a2，a3，a4，s，等参数的取值范围，按照不同的参数组合制作成一个数据表，如表1所示。

表1 不同参数组合

②将表中所得不同参数组合分别代入目标函数B（a1，a2，a3，a4，a5，s，x），并对其进行FFT分解，根据式（9）求得不同参数组合下各次谐波畸变率THD。

③依据求得各次谐波畸变率THD，求得其最小值THDmin，最终得到最优的参数组合，如表2所示。

表2 最优参数组合

在时刻t=12 μs时，通入激励电流幅值为25 mA，z=200 μm处Z轴方向磁感强度分量的分布图，如图6所示。此刻磁场分布十分接近于测量所需的基波脉振磁场。

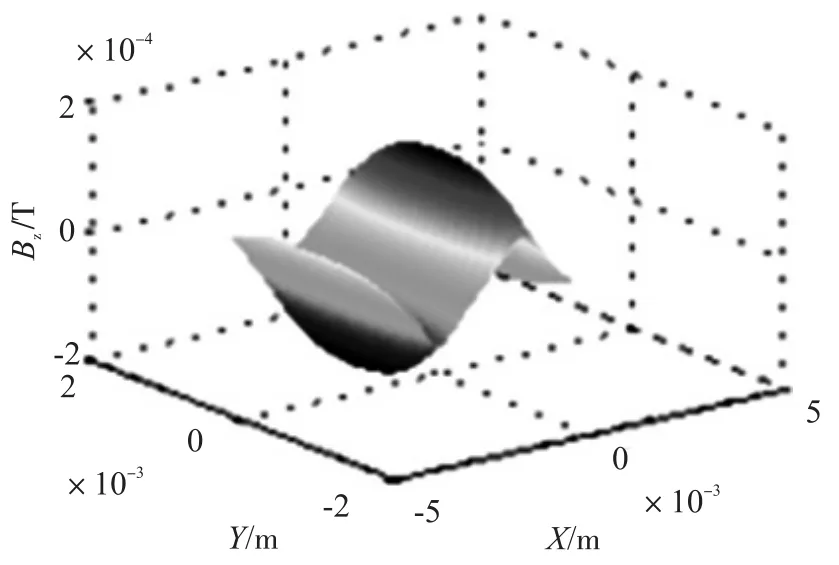
图6 Bz分量三维磁场分布

3 仿真实验验证与应用

3.1 结构仿真验证

平面线圈磁场分布在ANSOFT中采用瞬态求解器进行磁场分析，利用UG软件建立平面阵元的几何模型如图7所示，其中线宽为b=100 μm，通入激励电流幅值为25 mA，利用ANSOFT后处理模块得出z=200 μm处磁感应强度云图和矢量图，如图8和图9所示［16］。

从图中可以看出在t=12 μs时，多匝方形平面线圈产生的磁场强度分布接近于基波脉振磁场分布。

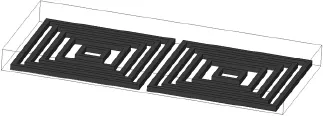
图7 平面线圈模型图

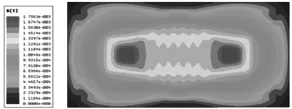
图8 平面线圈磁感应强度云图

图9 平面线圈磁感应强度矢量图

3.2 传感器模型仿真

根据平面线圈的最优化布置参数，在同一组感应线圈的情况下，建立基于平面线圈设计的新型时栅位移传感器和现有在导磁骨架上绕制多匝线圈方式的时栅传感器的仿真模型如图10（a）和图10（b）所示。模型参数为n=20，a20=10 mm，bmin=200 μm，节距W=41 mm，激励线圈中通入的激励电流幅值为25 mA。

图10 仿真模型与电行波信号

仿真得到的电行波信号如图10（c）和10（d）所示，其幅值变化和峰峰值变化如表3所示。

表3 仿真结果

理论上，电行波信号的过零点应该在时间坐标轴上等间距分布，相位变化呈线形分布，而实际上，由于传感器的误差导致过零点偏离坐标轴分布，其偏离程度反映了传感器的原始误差大小。

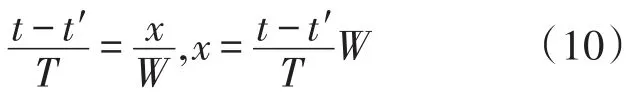
式中，t为某一位置理论过零点时间值，t′为某一位置的实际过零点时间值，T为电行波变化周期，W为节距，x为误差值

通过两种模型仿真结果的分析，相对于现有在导磁骨架上绕制多匝线圈的方式产生测量所需磁场分布的时栅，基于平面线圈设计的新型电磁式时栅产生的电行波信号较好，其随空间位置变化，行波幅值变化更小，线性度更好，原始误差更小。

4 实验结果

根据新型时栅传感器仿真模型布置参数，通过PCB工艺制作动尺与定尺，并建立实验平台，利用高精度光栅检测基于平面线圈设计的新型时栅位移传感器，精度标定实验台如图11所示。基于平面线圈设计的新型时栅定尺固定在衔铁上，并与大理石平台紧固，动尺与直线导轨连接，并随其运动。当运动一定位移时，以测量精度为±2 μm的海德汉封闭式直线光栅尺LF183为标准，时栅与光栅的差值就是传感器的原始误差，同时利用实验台检测现有传感器的原始误差，实测的原始误差曲线如图12所示。

图11 精度标定实验台

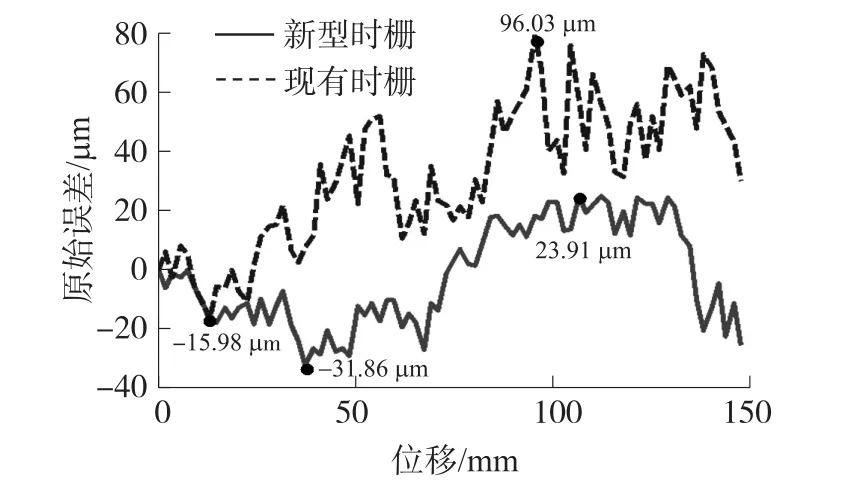
图12 原始误差曲线图

在感应线圈的运动过程中，由于安装精度，环境温度变化等因素的影响，使得误差随位移变化不断累积。

现有传感器的原始误差为-16 μm～81 μm，其峰峰值Vp-p0=97 μm。新型传感器的原始误差为-32 μm～24 μm，其峰峰值Vp-p1=56 μm。

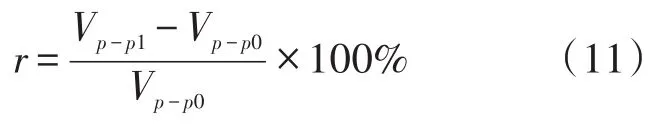
式中，r为原始误差的变化程度。

由式（11）知，新型时栅较现有时栅的原始误差减小了42.3%。

现有时栅位移传感器是通过在导磁骨架上绕制多匝线圈的方式产生测量所需的磁场分布。这种方法产生的脉振磁场分布函数中除了含有基波脉振磁场外，还含有很多谐波成分，从而引起较大的原始误差。而新型时栅通过优化传感器的敏感元件平面线圈从而产生测量所需的基波脉振磁场磁场分布，较现有时栅的磁场分布去除了大量的谐波成分，最终使得其原始误差有了较大的减小。

5 结论

①为了得到测量所需的基波脉振磁场，利用各次谐波畸变率THD最小的优化算法得到最优化布置参数，最终从设计源头提高传感器的测量精度。

②通过有限元分析软件ANSOFT对现有的电磁式时栅与基于平面线圈设计的新型时栅电磁场的仿真进行对比分析，新型时栅产生了较好的电行波信号，其行波幅值变化范围513.660 mV～542.408 mV，峰峰值变化为5.3%。

③建立实验台，采用光栅进行精度标定实验，新型时栅传感器原始误差为-32 μm～24 μm，较原有时栅原始误差有较大减小，本方法有利于时栅位移传感器的进一步发展。

［1］彭东林，刘小康，谭为民.时空坐标转换理论与时栅位移传感器研究［J］.仪器仪表学报，2000，21（4）：338-342.

［2］彭东林，陈锡侯，张天恒，等.直线式时栅位移传感器原理与结构［J］.自动化仪表，2012，33（6）：73-75.

［3］武亮，陈锡候，王阳阳，等.磁导调制型时栅位移传感器测量方法研究［J］.传感技术学报，2014，27（8）：1043-1048.

［4］陈锡侯，苟李，官云丽，等.基于单个读数头的角位移传感器自标定方法［J］.传感技术学报，2014，27（8）：1049-1053.

［5］刘小康，奚建平，郑方燕，等.基于AR模型的转台位置预测方法研究［J］.仪表技术与传感器，2012（3）：106-107，110.

［6］王鹏，丁天怀，傅志斌.微小平面电感线圈近场涡流效应模型［J］.清华大学学报，2009，49（5）：680-683.

［7］吴校生，陈文元，赵小林.磁悬浮转子微陀螺的微细加工工艺研究［J］.微细加工技术，2004（3）：68-72.

［8］Ramadan Q，VSamPer，Poenar D，et al.On-Chip Micro-Electro⁃magnets for Magnetic-Based Bio-Molecules Separation［J］.Jour⁃nal of Magnetism and MagneticMaterials，2004，281（2）：150-172.

［9］Fava Javier O，Ruch M C.Calculation and Simulation of Imped⁃ance Diagrams of Planar Rectangular Spiral Coils for Eddy Cur⁃rent Testing［J］.NDT&E International，2006，39（5）：414-424.

［10］汤蕴璆.电机学［M］.北京：机械工业出版社，2011：150-153.

［11］张兴红，陈渝光，彭东林，等.时栅位移传感器中的旋转磁场［J］.现代制造与工程，2002（9）：62-64.

［12］邝向军.方形载流线圈的空间磁场计算［J］.物理与工程，2006，16（1）：18-20，25.

［13］李开成.一种削弱永磁同步电机齿谐波电势的有效方法［J］.微电机，1995，28（3）：11-13.

［14］Liu Mingji，Yao Yu，Zou Jibin，et al.Error Analysis and Compensa⁃tion of Multipole Resolvers［J］.Measurement Science and Tech⁃nology，1999，10（12）：1292-1295.

［15］Bunte Andreas，Beineke，Stephan.High-Performance Speed Mea⁃surement by Suppression of Systematic Resolver and Encoder Er⁃rors［J］.IEEE Transon Industrial Electronics，2004，51（1）：49-53.

［16］赵博，张洪亮.Ansoft12在工程电磁场中的应用［M］.北京：中国水利水电出版社，2010：303-325.

黄 奔（1990-），男，江苏徐州人，重庆理工大学机械电子工程专业，在读硕士研究生，主要研究领域为计算机辅助测试技术与仪器，ben561@126.com；

彭东林（1952-），男，教授，工学博士，博士生导师，长期从事机电一体化、精密测量技术与仪器和智能传感器领域的研究工作，pdl@cqut.edu.cn；

武 亮（1986-），男，讲师，现为重庆大学在读博士，2011年毕业于重庆理工大学，获得硕士学位，主要研究方向为计算机辅助测试技术与仪器，ant56@126.com。

Construction method for fundamental wave of pulsating magnetic field with planar coils*

HUANG Ben，PENG Donglin*，WU Liang，ZHANG Tianheng
（Engineering Research Center of Mechanical Testing Technology and Equipment，Ministry of Education，Chongqing Key Laboratory of Time Grating Sensing and Advanced Testing Technology；Chongqing University of Technology，Chongqing 400054，China）

In order to reduce the original error of electromagnetic time-grating displacement sensor，a method based on planar coils for building the fundamental wave of pulsating magnetic field is proposed.Through the study of magnetic field generating method for traditional time-grating sensor and distribution of magnetic field generated by planar coils，an optimization algorithm that is restricted by Total Harmonic Distortion is presented.The optimal parameters of planar coils construction are obtained and verified in MATLAB and ANSOFT.Based on the structure parameters，a novel electromagnetic time-grating sensor with planar coils is designed.Calibrated by the optical grat⁃ing，the original error of the novel sensor is from-32 μm to 23 μm，42.3%lower than traditional time-grating sensor.

pulsating magnetic field of fundamental wave；the planar coil；total harmonic distortion；electromagnetic time-grating sensor

TH701

A

1004-1699(2015)10-1476-06

��7230

10.3969/j.issn.1004-1699.2015.10.010

项目来源：国家自然科学基金项目（51405049）；重庆理工大学研究生创新基金项目（YCX2014206）

2015-05-17 修改日期：2015-06-27