基于差动活门式反后坐技术仿真研究

王在森，程广伟，胡 勇，高 鑫，王 静

（西北机电工程研究所，陕西 咸阳 712099）

快速机动是现代火炮的重要指标之一，反后坐装置可大幅减小后坐力并可按要求控制后坐运动规律，是解决火炮威力与机动性这对矛盾的有效装置。

火炮发射时将产生很大的后坐冲击能量，一般采用液体气压式缓冲装置来吸收并耗散后坐能量［1］，活门式制退复进机是其中的典型结构之一。其原理是在工作缸（液压缸）和储气筒之间的液流通路上安装一个活门，利用弹簧控制活门开度来调整流液孔面积的变化，进而控制液体流动的液压阻力的变化规律［2］。

一般活门式阀型采用直流式平板阀，平板阀虽然设计简单，但阀芯承受较大的液体动压，存在明显的液压脉动冲击现象，在后坐开始阶段平板阀的开启往往具有滞后性，导致后坐阻力出现峰值，对火炮的结构和射击精度产生影响。

为了消除一般活门液压冲击现象，笔者应用差动补偿策略［3］，补偿办法是将活门受到的力“转移”到阀套上面，在阀套上切割出几条U 形槽口与活门形成差控体，改变了活门阀口的流动状态，从而改善活门阀芯的液动力，在后坐过程中，活门两侧弹簧力和液动力作用具有“自适应”过程，因此可获得变化比较平稳的后坐阻力曲线。

1 差动活门式缓冲装置结构原理

差动活门式缓冲装置是一套阀控系统，主要由制推杆、贮能气室器、液压差动控制阀（简称：差控阀）、活门节流阀、气液缸体，作用活塞等部分组成，其结构原理示意如图1所示，其工作原理是：制退杆在炮膛合力的作用下，推动液压缸中制退液向气室方向移动，在后坐开始时，后坐速度较小，此时液动力较小，活门在活门弹簧的作用下，起到了稳压作用，液体通过活门中心孔，此时活门只受稳态液动力，随着后坐速度的增加，稳态液动力随之增加，当超过活门弹簧稳压阀值后，活门相对差控阀体运动，从而打开了控制阀体流液孔，在活门弹簧的调节作用下，使得整个后坐过程中液压阻力保持在某一范围内，而不至于上升得过高。制退液推动气液活塞进行储能，最后由气液活塞将制退杆推回到原位，完成整个火炮后坐复进过程。

2 缓冲装置基本方程

2.1 腔体内流动基本假设

在建立差动活门式缓冲装置动力学方程时，关键是建立炮膛合力、后坐阻力、气室压力、活门弹簧参数和活门流孔面积的后坐诸元关系式。制退复进机内流体流动现象是十分复杂的，完全采用流固耦合的方法求解效率较低，为了工程上处理方便，在反后坐装置计算中常对缓冲器数学模型作以下假设：

1）制退液是不可压缩的。

2）制退液是一维的定常流。

3）气腔的气体为理想气体。

4）工作过程为绝热过程。

5）密封装置无泄漏。

差动活门式缓冲装置一般采用杆退式后坐方式，根据火炮发射原理可将缓冲器简化为二自由度动力学模型，如图2所示。图中m1为后坐部分质量，m2为活门 质量，x1为后 坐 位 移，x2为 活 门 位 移，Fpt为炮膛合力，R为后坐阻力。

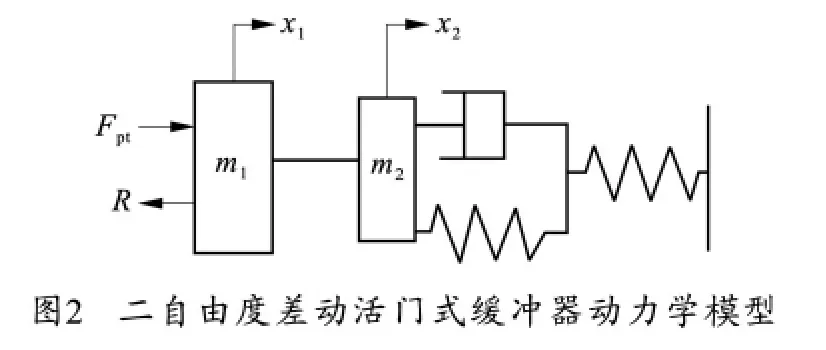
2.2 后坐部分运动微分方程

针对图2所示动力学模型，根据牛顿定律，列出运动微分方程。

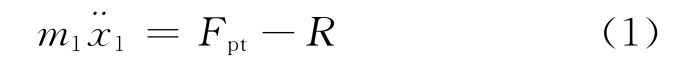
其中炮膛合力Fpt为

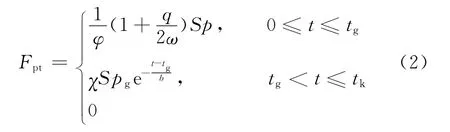
式中：φ为次要功计算系数；q为弹丸的质量；p为火药气体的平均压力；ω为装药量；S为炮膛断面面积；pg为后效期开始炮口压力；χ为炮口制退器冲量特征量；b为时间常数；t为以后效开始为起点的计算时间；tg为炮口时间点。

炮口制退器冲量特征量计算公式

式中：β为火药气体的作用系数；ηT为炮口制退器效率。

后坐阻力R计算公式为

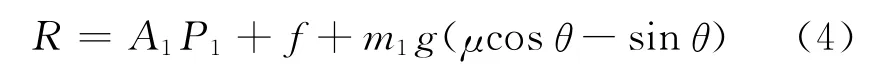
式中：μ为后坐部分与摇架导轨摩擦因数；θ为火炮高低射角；f为缓冲器活塞的摩擦力。

2.3 气腔压力计算

由基本假设3）～5）和热力学第一定律得

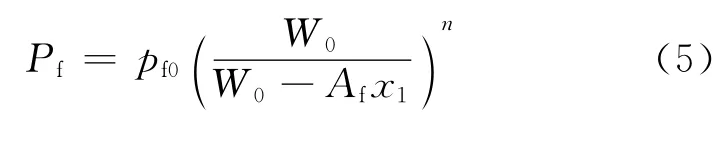
式中：Pf0、Pf分别为气腔的初始和工作压力；W0为气腔初始容积；n为气体的多变指数；Af为气腔截面积。

2.4 活门运动微分方程

活门在后坐过程中，会受到液动力、弹簧力、摩擦力等外力，其中液动力是由于活门运动使液流的速度矢量发生改变而产生的外力。因此，对活门液动力的准确计算和有效补偿，是提高反后坐计算精度的关键环节之一。

液动力分为稳态液动力和瞬态液动力，瞬态液动力在阀芯所受到的各种作用力中所占的比重不大，在一般液压计算中通常可以忽略不计，稳态液动力是指活门开口一定（稳定流动）时，由于流经阀腔和阀口的液流截面积及方向的改变而引起的液流速度的改变，导致液流动量的变化而产生的液动力［3］。稳态液动力又可称为动反力，它可分解为轴向分力和侧向分力。由于活门的油腔对称的设置，因此沿活门阀芯周围的侧向分力相互抵消。制退液在活门处的流动状态如图3所示。

根据缓冲器二自由度动力学模型，活门运动微分方程为

式中：k为活门弹簧刚度系数；F0为活门弹簧预压力；Fyj为活门静压力；Fyd为活门稳态液动力。

活门静压力为

式中：Ah1、Ah2分别为活门前后断面面积；Ph1、Ph2分别为活门前后两腔压力。

由活门腔体流体动量定理可得出，活门受到的稳态液动力为

式中：ρ为液体密度；Q为流体流量；ω1为流体入口速度；ω2为流体出口速度；α1为入口射流角；α2为出口射流角。

活门流量方程

式中：cd为阀口流量系数；Ax为流活门流液孔面积；ΔPh为活门入口和出口的压差。

活门流液孔面积Ax是关于活门位移的函数，如图4所示。

当差控阀体的侧壁漏口未打开时，Ax的值为活门本体中心孔的面积；当差控阀体的侧壁漏口打开时，Ax随活门位移的增大而增大，实现了变截面目的。为方便计算，将活门侧壁流液孔的面积等效到活门中心孔处，Ax的计算有如下关系描述：

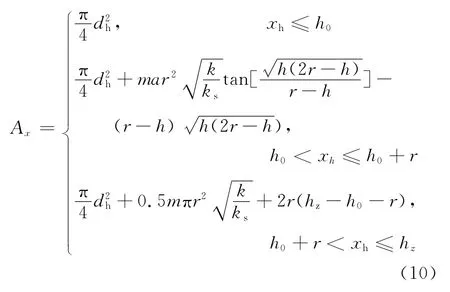
式中：dh为活门中心孔的直径。

2.5 差动活门式缓冲装置压力方程

差动式缓冲装置腔体由制退机腔体I、活门腔体II和气室腔体III构成，如图5所示。各腔压力关系和流速可由实际流体的白努利方程来描述。在后坐过程中由于活门的限流作用，引起各腔压力及流速变化，在变化过程中一部分以沿程损失形式耗散能量，另一部分以局部损失形式耗散能量。不过仅应用白努利方程不能完全确定各腔流体的状态，为此在建立差动式缓冲装置腔体压力方程时需联合活门流量方程式将压力改写成增量形式［4］。

即，P1＝ΔP1＋ΔP2＋ΔP3＋Pf。

从理论分析的角度可得出，液体压力损失和后坐速度的计算公式为

式中，ξ为液体的损失系数，计算中一般采用经验性公式，它与液体的几何尺寸、管壁的粗糙度、流动状态和液体的黏性等有关。

差动式缓冲装置腔体压力损失有截面突然收缩、液流的突然扩大、小孔的流动3种类型，具体表达形式如下：

式中：A0为出口面积；A1为入口面积；w1、w2、w3分别为各出口截面液体的流速；α收缩系数；γ为修正系数，对于一般突然收缩的圆孔形状可取γ＝0.5。

式（1）～（13）的方程构成了差动活门式缓冲器完备二自由度二阶微分方程组。

2.6 微分方程数值迭代方法

求解二自由度后坐微分方程时，由于膛压Ppt是以表格形式给出，不能用分离变量法直接积分求解，只能用数值法求解。应用二阶微分方程的迭代格式，设在微小的时间间隔Δt＝tn－tn－1内，对微分方程逐步积分，可得：

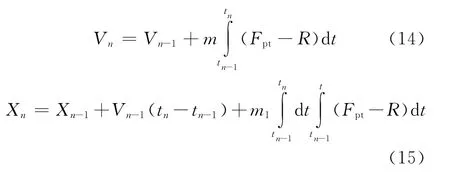
3 仿真计算和试验数据对比

基于以上建立的方程组和二阶微分方程迭代格式，应用Matlab软件，编写m 文件计算程序［5］。常温装药条件下，炮膛断面面积S＝1 650mm2，炮口初速v0＝1 000m／s，炮口压力pg＝55MPa，火药气体作用系数β＝1.6，装药量ω＝0.6kg，弹丸质量q＝1.85kg，后坐质量m1＝360kg，次要功系数φ＝1.1，活门弹簧刚度η＝4.8N／mm，制退液密度ρ＝1 100kg／m3，活门弹簧预压力11.25N，气室初压pf0＝7 MPa，气室初始容积W0＝8.5×105mm3，活门质量m2＝0.25kg，活门孔处的液压阻力系数ξ＝2.5，后坐部分与摇架导轨摩擦因数μ＝0.6，计算得到差动式反后坐装置的后坐诸元特征曲线及测试曲线，如图6～8所示。

经过对差动式反后坐装置后坐位移、速度以及后坐阻力数值计算和测试数据对比，可以看出后坐阻力相对误差不大于8.5%。后坐位移理论计算值与试验测试值相对误差不大于1.5%，后坐速度相对误差不大于3%。

后坐阻力数值计算相对误差较大，但根据后坐时序可以看出，其误差较大的时刻只出现在活门开启瞬间，对后坐速度、后坐位移不会造成明显影响。

4 制退液的温升计算

从能量的角度出发，制退机是一个耗散系统，在火炮后坐和复进过程中大部分不可逆地转化成了驻退机的热能。在考虑制退机液温升计算时，一般采用与制退机散热条件有关的修正系数，先计算单发射击时制退液净温升，然后计算火炮连发射击时制退液温度是否满足制退液使用的工作温度。

4.1 单发射击时制退液温升计算

式中：ΔT为单发射击时制退液温升；η为与制退机散热条件有关的修正系数，计算中取η＝0.85；vmax为自由后最大速度，vmax＝6.26 m／s；Ci为制退液比热系数，Ci＝3 255J／kg·℃；Cg为钢的比热系数，Cg＝483J／kg·℃；mye为制退液质量，mye＝2.11kg；mg盛装制退液筒的质量，mg＝5.7kg。

由式（15），代入以上计算参数可得

4.2 火炮持续射击发数n计算

火炮持续射击发数

式中：Tj为制退液沸点，Tj＝90℃；T0为环境温度，T0＝50℃。

通过计算可得

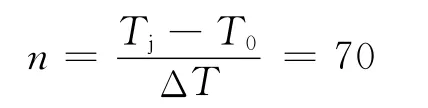
通过制退机散热条件有关的修正系数，计算了单发射击时制退液净温升，根据制退液沸点确定了火炮连发射击发数。

5 结论

通过理论建模，数值仿真计算和试验测试相结合的方法，分析了基于差动式活门反后坐装置后坐诸元及活门液动力特性，可得出以下结论：

应用二自由度二阶微分方程可建立完备的活门式反后坐运动方程；应用差动式活门可改善活门阀芯的液动力，可获得变化比较平稳的后坐阻力；应用一维的定常流理论求解制退液流体力学问题，能够满足工程设计需求且有效提高了计算效率；采用与制退机散热条件有关的修正系数，计算单发射击时制退液温升计算，确定火炮连发射击时制退液温度工况条件。

（References）

［1］戴劲松，刘振，王茂森，等.高频冲击作用下高阻尼气液缓冲装置动态仿真［J］.火炮发射与控制学报，2012（1）：22－25.DAI Jinsong，LIU Zhen，WANG Maosen，et al.The dynamic simulation for high damping factor pneumatichydraulic precision buffer under the effect of high frequency shocks［J］.Journal of Gun Launch ＆Control，2012（1）：22－25.（in Chinese）

［2］刘荣华，高跃飞，李小平，等.基于AMESim 的后坐活门液压阻力特性研究［J］.机床与液压，2011，39（11）：33－35.LIU Ronghua，GAO Yuefei，LI Xiaoping，et al.Study on the characteristics of recoil resistance of valve based on AMESim［J］.Machine Tool ＆Hydraulics，2011，39（11）：33－35.（in Chinese）

［3］段少帅，姚平喜，张恒.滑阀稳态液动力产生原因与补偿方法［J］.流体传动与控制，2010（3）：27－30.DUAN Shaoshuai，YAO Pingxi，ZHANG Heng.Steady－state fluid force of spool valve and its compensation method［J］.Fluid Power Transmission ＆Control，2010（3）：27－30.（in Chinese）

［4］孙振华，张世富，张起欣，等.差动式快开阀开阀过程动力学分析与仿真［J］.后勤工程学院学报，2011，27（3）：35－41.SUN Zhenhua，ZHANG Shifu，ZHANG Qixin，et al.Dynamics analysis and simulation of open－on valve procedure of differential control fast－open valves［J］.Journal of Logistical Engineering University，2011，27（3）：35－41.（in Chinese）

［5］汪云峰，谭宗柒.基于AMESim／Matlab的液压缓冲器仿真与优化［J］.机床与液压，2008，36（3）：167－168.WANG Yunfeng，TAN Zongqi.Simulation and optimization of hydraulic shock absorber based on AMESim／Matlab［J］.Machine Tool ＆ Hydraulics，2008，36（3）：167－168.（in Chinese）