不确定数据流上的并行反Skyline 查询

张建荣，毛宇光

(南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

0 引言

在大量的应用中，数据都以数据流的形式出现。在诸如传感器网络、网络监控、金融股票分析以及通信数据管理等应用中，数据的到达呈现出一种连续、实时、大数据量以及无法预知等特点，这些数据可被看成是一条顺序的、无穷尽的数据信息序列。而且由于传输或环境噪声等原因，数据一般具有不确定的特性。由于该类型数据的广泛存在，不确定数据流上的查询研究具有重要的应用价值。

不确定数据流上的反Skyline 查询对于多目标决策具有重要的意义。如在环境监测中，部署在不同地点的传感器不断地将数据传输至中心节点，通过对这些数据进行反Skyline 查询可以实时获得对决策有用的信息。现有的查询处理都采用单机算法，而在以下情况下:

1)不确定数据流上数据到达的速度过快;

2)滑动窗口大小太大;

3)数据维度较大的时候优化或剪枝策略效果不明显，单机算法虽然采取了多种优化机制，但依然无法满足查询的实时性要求。

本文在已有的研究基础上，提出不确定数据流上反Skyline 查询的并行处理算法PRSUDS(Parallel Reverse Skyline Query over Uncertain Data Streams)，并通过大量实验验证该算法的有效性。

1 相关工作

自从Borzsonyi 等人［1］于2001 年首先将Skyline查询引入数据库研究领域以来，与Skyline 查询相关的研究获得了极大的丰富并取得了许多成果。对于确定数据集上的Skyline 查询，研究人员提出了许多高效算法，包括BNL 算法［1］、D＆C 算法［1］、SFS 算法［2］、NN 算法［3］和BBS 算法［4］等，其中BBS 算法被证明是I/O 最优的。为解决数据中存在的不确定性问题，Pei 等人［5］首先针对不确定数据中的Skyline 查询提出了概率Skyline 查询的概念。而反Skyline 查询则由Dellis 等人［6］在2007 年首先提出，作为Skyline 查询的一种变体，反Skyline 查询在诸如环境监测、商业决策以及产品营销投资等领域均有重要的应用。关于反Skyline 查询的研究已取得许多重要成果。Lian 等人［7］首先研究了不确定数据集合上的概率反Skyline 查询问题，并给出了在单色(Monochromatic)环境和双色(Bichromatic)环境中反Skyline 查询的计算方法。Wang 等人［8］研究了传感器网络中的反Skyline 查询，并提出了半支配的概念，半支配概念的提出为反Skyline 查询的处理提供了极大便利。Zhu 等人［9］提出了一种基于DC-tree 的确定数据流上的反Skyline 查询算法。Bai Mei 等人［10］针对不确定数据流上的反Skyline 查询问题进行了研究，并提出了相应的单机算法OPRS。OPRS 算法在已有研究的基础上，基于R 树索引结构采用若干概率剪枝策略来加快反Skyline 查询的计算。作为不确定数据流上反Skyline 查询的单机算法，OPRS 算法将作为本文提出的并行算法的对照。

2 问题定义

设A={A1，A2，·，Ad}是一组值域的集合，O=A1×A2×·×Ad是一个d 维空间，A1，A2，·，Ad被称为空间O 的属性或维。设U 为来自空间O 的一个d 维数据集，u 为U 中的一个数据对象，则u［i］(i ∈{1，2，·，d})表示对象u 在第i 维上的取值，不失一般性令u［i］∈(0，1］，且以小值为较优值。

定义1 动态支配。给定1 个d 维查询点q 和2个相同维的数据对象u 和v，如果满足以下条件，则称u 相对于查询点q 动态支配v，记为u≺qv:

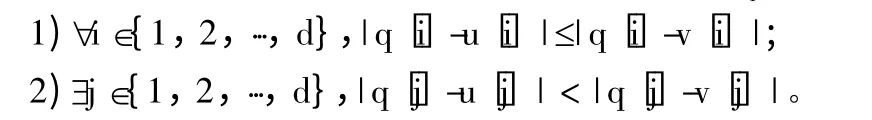
定义2 概率反Skyline 查询。给定一个概率阈值p、一个d 维不确定数据集U 以及一个d 维的查询点q，对于U 中的每个数据对象都有一个存在概率与之关联，如果数据集U 中的一个对象u 的反Skyline概率大于或等于阈值p，则u 属于U 中关于查询点q的概率反Skyline 集合，记为p -RSKYq(U)={u∈U|PRSKY(u)≥p}，其中:

表示对象u 的反Skyline 概率。

定义3 半支配。给定1 个d 维查询点q 和2 个相同维的数据对象u 和v，如果满足以下条件，则称u关于查询点q 半支配v，记为:

定理1［8］如果v 关于u 动态支配q，则v 关于q半支配u，反之亦然。

根据定理1，式(1)可以很容易转化为:

由式(2)可知一个对象的反Skyline 概率为其存在概率与所有半支配其的对象均不存概率的乘积。

本文所讨论的是不确定数据流上的反Skyline 的查询问题。同此前不确定数据流上的相关工作［11］一致，本文同样采用基于计数的滑动窗口模型，将不确定数据流定义为不确定元组的序列:{(u1，p1)，·，(uk，pk)，·}，其中:(ui，pi)代表一条不确定元组，ui为来自空间O 的对象;pi表示对象ui的存在概率(0 ＜pi≤1)，对象之间相互独立;i 表示对象ui第i 个进入窗口，在实际的实现中每个对象都会对应一个属性id，用以表示其在数据流上的序列号，同时也作为唯一性标识。在基于计数的滑动窗口模型中，如果窗口大小为W，则每个对象的生命周期跨度为W 个序列号，即对象ui在区间［i，i +W -1］内是有效的(或活跃的)，当窗口已满时，新对象的到来将使最老的对象过期。用N 代表最新进入窗口的对象的序列号，当窗口已满时，窗口内的对象集合S={uN-W+1，·，uN}，不确定数据流上的反Skyline 查询即是实时维护集合S 中的反Skyline 集合。函数k(u)返回对象u到达窗口的时间点，k(u)值越小表明对象u 到达窗口的时间越早;在基于计数的滑动窗口模型中采用序列号作为对象到达的时间点，如k(u)=1 表示对象u的序列号为1;在实际的实现中可设一个全局序列号，当一个对象到达窗口时可将全局序列号赋予该对象，然后全局序列号进行一次自加。

定义4 不确定数据流上的反Skyline 查询。给定一个概率阈值p、一个查询点q 以及一条不确定数据流S，在其上的概率反Skyline 集合记为

其中:

根据定理1，式(3)可转化为:

3 并行处理概述

在对静态数据的查询进行并行处理时，大部分文献的基本思想为:采用某种划分方法将数据集划分为若干子集，并将各子集传输至相应的并行节点，各并行节点只对本地数据进行处理并将处理结果传输至中心节点，最后由中心节点对各并行节点的处理结果进行合并。目前主流的划分方法有基于网格(Gridbased)的划分方法［12-13］和基于角度(Angle-based)的划分方法［14-15］。

在数据流的并行处理中，由于数据流不断到达，因而静态数据并行处理中先划分然后合并的方法并不能直接使用，通常的方法是采用某种策略将到达的数据不断分发至相应的节点进行处理。文献［16］提出了基于滑动窗口划分的PSUDS 算法，该方法将整个数据流的滑动窗口大小分成若干等份，每个并行节点只负责其所对应子窗口内的对象的处理。而文献［17］为克服PSUDS 算法中各并行节点需要相互通信的缺点，进一步提出了基于2 级并行查询处理模型的并行算法。滑动窗口划分具有简单、易于实现的优点，但同时也存在并行处理效果不佳的缺点。本文的方法为:采用基于角度划分的策略对整个空间O 进行划分，各并行节点负责相应的数据空间的处理，而当一个新的数据对象到达时对其坐标进行超平面映射以确定其所对应的分发节点。

与静态数据集上的并行处理不同，数据流上的并行处理中各并行节点所担任角色的划分更加复杂。本文采用同文献［18-19］相似的并行处理设置(Parallel Processing Settings)，其网络结构如图1 所示，在该并行处理设置中所有的并行节点根据其所担任角色的不同可分为3 类:

1)监控节点(Monitor Node):该节点负责将新到的数据流对象分发给各并行计算节点，并且协调各并行计算节点完成反Skyline 查询处理任务，因而监控节点的作用可概括为接收、分发以及控制/协调3 种。

2)并行计算节点(Peer Node):该节点负责处理具体的查询处理任务，包括新对象、过期对象的处理以及数据流中对象反Skyline 概率的维护，所有的并行计算节点之间都可相互通信，如图1 所示。

3)查询节点(Query Node):该节点负责从各个并行计算节点中收集反Skyline 查询的结果，并将其呈现给用户。

监控节点、并行计算节点和查询节点只是根据节点所担任的角色进行划分，在实际的实现中同一个节点可担任多种不同的角色，如监控节点与查询节点一般由同一节点担任，而监控节点或查询节点本身也可作为并行计算节点进行局部的查询处理。

图1 并行处理的网络结构

4 PRSUDS 算法

4.1 分发策略

监控节点M 在接收到新到对象时需要采用某种机制将其分发至特定的并行处理节点进行处理，在文献［16］中采用了基于滑动窗口划分的机制，该机制相当于对整个数据流窗口进行水平分割为若干子窗口，一个子窗口由一个并行处理节点负责维护。

PRSUDS 算法中分发策略的基础是空间划分，即根据坐标对空间进行划分。由于空间O 根据查询点q 可分为2d个子空间，不同子空间的对象之间不具有关联，因而空间划分为对各子空间的进一步划分。如图2(a)所示，每个子空间划分为3 个部分，每个部分由一个并行计算节点处理，可见每个并行计算节点负责每个子空间中的一个分区。而空间划分的方法为基于角度划分，实现的方法为先将对象坐标映射至一个超平面中，如图2(b)所示，映射的具体公式如式(5)所示。

图2 PRSUDS 算法分发策略原理

经过空间划分，不同的并行计算节点只负责相应空间内对象的处理。当一个对象到达监控节点M时，节点M 将首先计算新到对象所属的分区，最后根据计算结果将该对象分发至相应的并行计算节点。

PRSUDS 算法采用的分发策略相当于将到达监控节点M 的不确定数据流S 分割为在各并行计算节点上流动的若干条子数据流S1，S2，·，Sn(n 为并行计算节点数量)，(u)和PGLOBAL(u)分别表示在子数据流Si和全局数据流S 上所有半支配u 的对象均不存在的概率，则有:

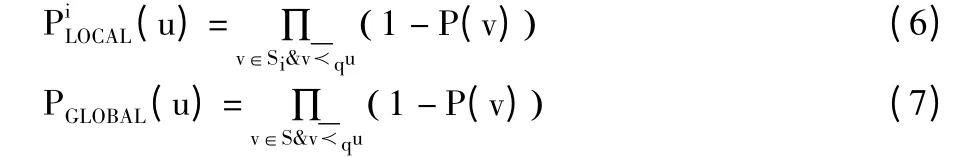
定理2 采用本节的分发策略对不确定数据流S划分子流后，对象u 的反Skyline 概率满足:

证明:对S 进行划分后任意2 个子流Si和Sj有Si∩Sj=φ(1 ≤i，j ≤n)，且=S，所以:

综上所述，定理2 得证。

由定理2 可知，本文采用的分发策略不会对不确定数据流S 上的反Skyline 查询结果造成影响。

4.2 并行处理框架

图3 并行处理框架

PRSUDS 算法的并行处理框架如图3 所示，M 节点根据4.1 节论述的基于角度划分的分发策略将不确定数据流中的每个对象分发至各并行计算节点，而新对象反Skyline 概率的计算、新对象到达以及对象过期时的反Skyline 概率更新等处理任务则由各并行计算节点完成，整个过程的控制协调由M 节点负责。从图中可以看出各并行计算节点是互连的，表明各节点相互之间需要进行通信。

PRSUDS 算法采用的并行处理框架具体实现如算法1 所描述，算法中采用队列Q 记录每个对象的分发节点。当有新对象到达M 节点时，首先判断窗口是否已满，是则将队列Q 记录的过期对象的分发节点从队头弹出，并向该分发节点发送＜CTR_EXP ＞消息，表示开始处理过期对象，此时该分发节点将作为临时的汇总节点;处理完过期对象之后则确定新到对象的分发节点，并向该节点发送＜CTR_NEW，unew＞消息，表示开始新到对象的处理，此时该分发节点作为临时的汇总节点。汇总节点作为临时的控制节点控制其它的并行计算节点完成相应的处理，而这些并行计算节点在处理完成之后分别向当前的汇总节点发送完成消息，汇总节点在收到所有的处理完成消息之后向M 节点发送处理完成消息，然后由M 节点控制下一轮处理的开始。

算法1 并行处理框架

输入:不确定数据流S，概率阈值p，滑动窗口大小W，查询点q

输出:将S 中的对象分发至各并行节点，并动态维护S 上的反Skyline 查询结果

算法2 描述了各并行计算节点上的处理，每个并行计算节点上的处理逻辑可概括为:接收消息和响应消息。当节点接收到＜CTR_EXP ＞消息时，该节点作为处理过期对象时的汇总节点，向除自身之外的其它并行计算节点发送＜PRO_EXP，uold＞消息，之后对本地的对象进行概率更新，当收到所有的响应消息时向M 节点发送＜FINISH ＞消息;当收到＜PRO_EXP ＞消息时，开始处理过期对象，完成之后向汇总节点发送＜FINISH ＞消息;当接收到＜CTR_NEW ＞消息时，该节点作为处理新到对象时的汇总节点，向除自身之外的其它并行计算节点发送＜PRO_NEW，unew＞消息，发送完消息之后计算局部的(unew)并更新被unew半支配的对象的反Skyline 概率，当收到所有的响应消息后计算新到对象的PGLOBAL(unew)并向M 节点发送＜FINISH ＞消息;当收到＜PRO_NEW ＞消息时，开始计算局部的(unew)并更新被unew半支配的对象的反Skyline 概率，完成之后向汇总节点发送＜FINISH ＞消息。

算法2 并行计算节点Pi处理

输入:从M 节点或汇总节点接收的处理消息

输出:向M 节点或汇总节点返回消息

5 算法分析

并行算法的优势体现在某些特定情况下较单机算法具有更快的查询响应速度，而衡量的标准即是加速比，即单机算法对并行算法响应时间的比值大小。与单机算法不同，并行算法增加了通信以及同步等额外开销，而且在反Skyline 查询的优化处理上也不尽相同，因而并行算法加速比的分析主要体现在这些方面。各并行节点完成一轮处理所用的时间可分为:

1)同步时间。同步时间主要包括确定分发节点的时间以及计算全局概率的时间等，这些时间与数据的规模及处理的实际情况关系不大，所以设其为一个固定时间tsyn。

2)通信时间。并行节点之间通过消息通信实现并行处理逻辑及各种同步操作，前文已经提到分为控制消息和处理消息2 大类，考虑到单次通信的时间较短，将一轮处理所需要的通信时间为tcom。

3)处理时间。算法一轮处理可分为2 个阶段，分别为处理过期对象阶段和处理新到对象阶段，由于汇总节点需要等待该阶段其它所有并行节点完成处理才能进入下一阶段，所以每个阶段计算所消耗的时间分别为:

在算法负载均衡性能良好的情况下Tphase1与(1 ≤i ≤n)、Tphase2与(1 ≤i ≤n)之间的差异很小。所以并行算法进行一轮处理所使用的时间为:

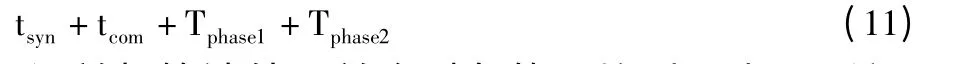
设单机算法处理单个对象的平均时间为ts，所以并行算法的加速比为:

6 实验验证

6.1 并行加速验证

本文采用VC ++6.0 实现PRSUDS 算法，为更好地体现算法的性能，采用文献［10］中OPRS 算法作为对照。实验环境为:Windows 7 操作系统、主频2.10 GHz Intel(R)Core(TM)i3 处理器、3 GB DDR3内存。实验采用文献［1］提供的合成数据作为实验数据集。

本节将从滑动窗口大小、维度、概率阈值以及并行计算节点数量4 个角度考察并行算法的时间性能。

1)滑动窗口大小。

图4 滑动窗口大小的影响

首先考察的是滑动窗口大小对PRSUDS 算法时间性能的影响。图4 显示的是滑动窗口大小对PRSUDS 算法时间性能影响的实验结果。从图中可以看出滑动窗口大小从0.5 MB 逐渐增加至1 MB，开始时单机算法与并行算法的响应时间相差不大，这是因为当滑动窗口不太大的时候单机算法的处理能力能够胜任，而且并行算法还需要付出额外的通信及同步时间;但当滑动窗口增加到足够大时，单机算法与并行算法响应时间具有明显的差距，这表明并行算法能够满足滑动窗口过大时单机算法无法及时响应的情况。

2)维度。

图5 维度的影响

图5 显示的是维度对并行算法时间性能的影响。当滑动窗口大小为0.5 MB、并行计算节点数量为8时，维度从2 增加到6。从图5 中可以看出当维度为2 时PRSUDS 算法的响应速度略快于OPRS 算法，而当维度增加至6 时差距则非常明显，这表明并行PRSUDS 算法能够有效处理维度过大时的查询处理。

3)概率阈值。

图6 概率阈值的影响

图6 显示的是概率阈值对并行算法时间性能的影响。当滑动窗口大小为0.5 MB、并行计算节点数量为8、维度为4 时，概率阈值从0.25 逐渐增大至0.5。从图中显示的结果可以看出PRSUDS 算法和OPRS 算法的响应时间均随概率阈值的增大而减少，这与之前的分析一致，而PRSUDS 算法的响应时间一直小于OPRS 算法。

4)并行计算节点。

最后考察的是并行计算节点的数量对PRSUDS算法时间性能的影响。图7 显示的是维度为4、滑动窗口大小为0.5 MB 时并行计算节点由1 个增加到16 个时实验结果。由于考察的是并行计算节点的影响，所以图中OPRS 算法的响应时间保持不变，而PRSUDS 算法的响应时间随着节点数的增加而减少;当节点数量小于2 个的时候单机算法的性能要优于并行算法，而当节点数量大于2 个的时候并行算法的性能开始逐渐优于单机算法，且当节点数量增加到8的时候，并行PRSUDS 算法的响应时间趋于平稳，这是因为当并行计算节点数量增加到一定程度时这些计算节点的计算能力已经足够，再增加也不会明显加快响应时间。综上所述，PRSUDS 算法发挥了并行算法的优势，适合流速过快、高维度数据流上的反Skyline 查询处理。

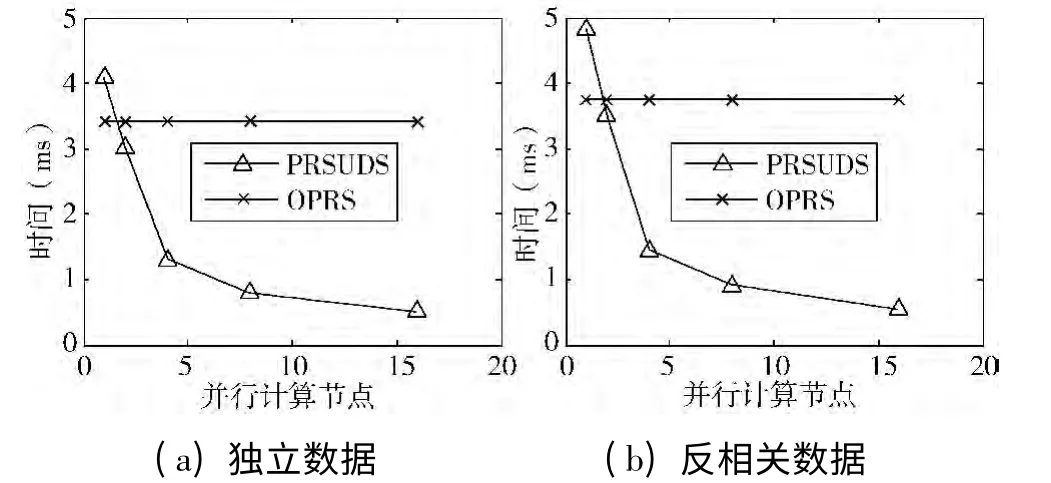
图7 并行计算节点数量的影响

6.2 负载均衡测试

图8 负载均衡测试结果

PRSUDS 算法采用基于角度划分的数据流对象的分发策略，每个并行计算节点负责自身所在区域的对象处理，对于该方法的负载平衡性能需要进行必要的测试。对于各并行计算节点的实际负载测试结果如图8 所示。在测试中随机选取10 个并行计算节点，分别统计其一段时间内PRSUDS 算法处理单个对象的平均用时，测试结果为维度为6、滑动窗口大小为1 MB 时统计得出。从图中可以看出选取的各并行计算节点的单个对象平均处理时间较为接近，表明PRSUDS 算法采用的分发策略具有较好的负载均衡特性，能够尽量减少各节点间的空等时间。

7 结束语

针对单机算法的某些局限性，本文提出了一种不确定数据流上的反Skyline 并行查询算法PRSUDS，实验表明并行算法在各种条件下均较单机具有更好的可扩展性(Scalability)，更能适应实际应用的需求。下一步的工作主要包括:进一步优化算法的并行处理框架，以减少并行或同步所需要的时间;在各并行节点的局部处理中，研究如何采用索引结构和剪枝策略等手段对局部计算过程进行优化。

［1］Borzsonyi S，Kossmann D，Stocker K.The Skyline operator［C］// Proceedings of the 17th IEEE International Conference on Data Engineering.2001:421-430.

［2］Chomicki J，Godfrey P，Gryz J，et al.Skyline with presorting［C］// Proceedings of the 19th IEEE International Conference on Data Engineering.2003，3:717-719.

［3］Kossmann D，Ramsak F，Rost S.Shooting stars in the sky:An online algorithm for Skyline queries［C］// Proceedings of the 28th International Conference on Very Large Data Bases.2002:275-286.

［4］Papadias D，Tao Yufei，Fu G，et al.An optimal and progressive algorithm for Skyline queries［C］// Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data.2003:467-478.

［5］孙圣力，戴东波，黄震华，等.概率数据流上Skyline 查询处理算法［J］.电子学报，2009，37(2):285-293.

［6］Dellis E，Seeger B.Efficient computation of reverse Skyline queries［C］// Proceedings of the 33rd International Conference on Very Large Data Bases.2007:291-302.

［7］Lian Xiang，Chen Lei.Monochromatic and bichromatic reverse Skyline search over uncertain databases［C］// Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data.2008:213-226.

［8］Wang Guoren，Xin Junchang，Chen Lei，et al.Energy-efficient reverse Skyline query processing over wireless sensor networks［J］.IEEE Transactions on Knowledge and Data Engineering，2012，24(7):1259-1275.

［9］Zhu Ling，Li Cuiping，Chen Hong.Efficient computation of reverse Skyline on data stream［C］// Proceedings of the 2009 IEEE International Joint Conference on ComputationalSciences and Optimization.2009，1:735-739.

［10］Bai Mei，Xin Junchang，Wang Guoren.Probabilistic reverse Skyline query processing over uncertain data stream［C］// Proceedings of the 17th International Conference on Database Systems for Advanced Applications.2012:17-32.

［11］Cormode G，Garofalakis M.Sketching probabilistic data streams［C］// Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data.2007:281-292.

［12］Wang Wei，Yang Jiong，Muntz R.STING:A statistical information grid approach to spatial data mining［C］// Proceedings of the 23rd International Conference on Very Large Data Bases.1997:186-195.

［13］Rocha-Junior J B，Vlachou A，Doulkeridis C，et al.AGiDS:A grid-based strategy for distributed Skyline query processing［C］// Proceedings of the 2009 International Conference on Data Management in Grid and Peer-to-Peer Systems.2009:12-23.

［14］Vlachou A，Doulkeridis C，Kotidis Y.Angle-based space partitioning for efficient parallel Skyline computation［C］//Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data.2008:227-238.

［15］Kohler H，Yang Jing，Zhou Xiaofang.Efficient parallel Skyline processing using hyperplane projections［C］// Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data.2011:85-96.

［16］王广东，王意洁，李小勇，等.不确定数据流上的并行Skyline 查询算法［J］.计算机科学与探索，2012，6(12):1116-1125.

［17］赵越，王意洁，王媛，等.一种高效的不确定数据流并行Skyline 查询处理方法［J］.计算机研究与发展，2013，50(z2):132-139.

［18］Afrati F N，Koutris P，Suciu D，et al.Parallel Skyline queries［C］// Proceedings of the 15th International Conference on Database Theory.2012:274-284.

［19］Park S，Kim T，Park J，et al.Parallel Skyline computation on multicore architectures［C］// Proceedings of the 25th IEEE International Conference on Data Engineering.2009:760-771.