择优学习多个体差分算法求解约束优化问题

付玉珍，周洁文，邵龙秋，张 慧

(1.茂名职业技术学院计算机工程系，广东 茂名 525000;2.广东省石化装备故障诊断重点实验室，广东 茂名 525000)

1 约束优化问题数学描述

不失一般性，以最小化问题为例，约束优化问题可描述为:

其中:x=(x1，x2，…，xn)是一个n 维向量，f(x)为目标函数，gi(x)≤0 和hi(x)=0 分别为q 个不等式约束和m-q 个等式约束，函数f(x)、gi(x)和hi(x)可以是线性和非线性实值函数，li和ui分别是决策变量xi取值的下界和上界。若搜索空间记作S，满足所有约束条件的可行解空间为F=，则有F⊂S。若x 满足所有的约束，则称其为一个可行解;若x 至少违反了一个约束，则称其为不可行解。约束优化问题就是在F 空间内搜寻使目标函数达到最小值的解。

2 传统差分算法及其相关的改进算法

差分算法由Storn 和Price［1］于1995 年提出，它通过群体内个体间的合作与竞争产生群体智能指导优化搜索，具有记忆个体最优解和种群内信息共享的特点，采用实数编码。基于差分的简单变异操作和一对一的竞争生存策略，使得算法遗传操作简单且具有较强的全局收敛能力和鲁棒性。由于差分算法这种简单高效的特性，差分算法已成功应用到众多领域，其中将差分算法用于求解约束优化问题的研究主要集中在算法搜索能力的提高与约束处理技术的使用。近十几年以来很多改进的差分算法相继被提出用于改进算法的搜索性能，如文献［2］采用父代个体产生多个子代个体，从多个子代个体当中选择一个最优个体进入下一代来提高算法的搜索性能，但所有父代个体产生相同多的子代个体，并未考虑个体之间的优劣。文献［3］提出一种自适应差分算法，引入一种衰老机制，当算法陷入局部最优的时候重新生成个体替换衰老的个体。文献［4-5］提出基于ε 水平比较的差分算法，该方法在可行域比较小的情况下可以显著减少评估次数，但其收敛精度和鲁棒性还需进一步提高。文献［6］指出有效的变异策略和合适的参数设置可以显著提高差分算法的性能，但如何选择变异策略和合适的参数需要进一步研究。文献［7］通过自适应调节缩放因子和交叉率来搜索最优解。进化算法求解约束优化问题能力除了与进化算法自身有关外，还与所采用的约束处理技术密切相关，文献［8］采用改进算法的同时，构造了一种个体比较准则，引导搜索过程更好地向最优解靠近。可以看出如何提高算法的搜索性引起了广泛研究，本文在文献［9］所提COMDE 算法的基础上加入择优策略和克隆策略，使其快速定位到最优解区域的同时提高求解精度，提高原算法的搜索性能。

3 本文提出的算法

通过分析，算法首先要搜索到可行域，然后在可行域中找到最优解，本文算法(PLMIDE)通过择优学习策略在搜索空间内快速找到可行域，通过克隆策略在可行域的最优解区域展开更详尽的搜索，最终找到最优解。

3.1 约束处理机制及比较规则

差分算法是一种无约束的搜索技术，用于求解约束问题需结合某种约束处理机制，常用的约束处理技术有:惩罚函数法［10］、Deb 准则［11］、随机排序法［12］、多目标法［13］和ε 约束［14］等。本文算法采用的约束处理方法为区分可行解和不可行解的多目标法，首先将等式约束条件转换为不等式约束条件|hk(xi)| -ε＜0，等式约束条件的容忍因子ε 是一个非常小的大于0 的实数，cv(xi)为个体i 的违约函数值，其反映了个体xi的不可行性。

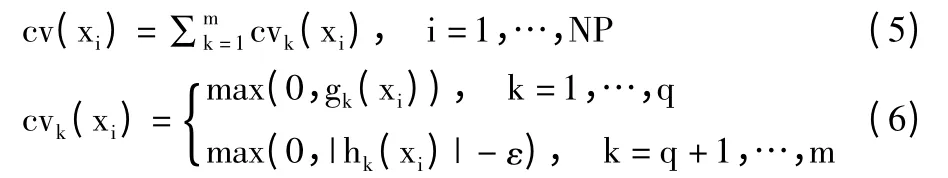
采用Deb 的比较准则:1)可行解总是优于不可行解;2)若2 个解均可行，则目标函数值小的解为优(以求最小值为例);3)若2 个解均不可行，则约束违反程度小的解为优;如式(7)所示，其中f 为目标函数值。

通过以上比较准则可以对群体做一个排序。

3.2 择优学习策略［15］

根据比较准则排好序的群体中，排在个体i 前面的个体都是比其优秀的个体，这些优秀个体可以指导个体i 的学习，则第i 个个体有i -1 个个体可以用来选择参与进个体i 的变异。择优学习策略如图1 所示。

图1 择优学习策略

r1、r2、r3、r4的取值为:

其中:i 表示第i 个个体，j 表示第i 个个体的第j 维分量，G 表示个体进化到第G 代，r1、r2、r3、r4标识群体中的不同个体，F0、F1、F2是缩放因子。i ＞4 是为了保证DE 有足够多个体用于个体i 的变异操作，jrand∈［1，d］，其中d 为个体的维数，用于保证个体每次至少有一位变异。

在众多的变异算子中，DE/best/1/bin 和DE/rand-to-best/1/bin 被证明效果优于其他变异算子［16］，将择优学习策略应用到这2 种变异算子中，在进化初期侧重变异算子2，随着进化过程选择使用变异算子1 的概率增加，进化后期2 种变异算子趋于平衡，这种择优学习的混合变异算子可以提高变异的有效性，加快个体向最优解靠近，最终提高算法的收敛速度。

3.3 克隆策略

为了增加群体的多样性，如文献［2］所述，父代个体不再是产生一个子代个体，每个父代个体产生nc 个子代个体，从nc 个子代个体中选择最优个体进入下一代，克隆操作有效地扩展了搜索空间，但是文献［2］中nc 选择某固定值，本文根据父代个体在群体中的排名，动态生成nc 个子代个体，ncβ·」，β 为克隆倍数，本文取值为1，r 为个体在群体中的排名，NP 为群体数目，该策略可以保持群体多样性的同时加大对优秀个体所在区域的搜索。

3.4 算法相关参数设置

算法中涉及的参数采用自适应方式产生，算法中相关参数有容忍因子ε，缩放参数F0、F1、F2，变异选择概率Pf，种群个数NP。

1)等式约束条件的容忍因子ε，通常ε 取值为0.000 1，本文随迭代次数自适应地调整，根据文献［4］，修改为ε=0.0001·，0 ＜G ＜Gmax。

2)因使用了混合变异策略，变异选择概率Pf随迭代次数变化，主要用于权衡群体的全局搜索和局部搜索，开始侧重变异策略2，随着迭代次数的增加，Pf的值越来越大，算法侧重混合策略的变异，防止群体陷入局部最优。Pf=0.5-Math.pow(1 -G/Gmax，4)。

3)缩放因子F0、F1、F2决定了差分向量的缩放比例，本文参数取值见表1，为了增大最优解的导向作用，取F1＞F2。

表1 缩放因子取值

3.5 算法伪代码

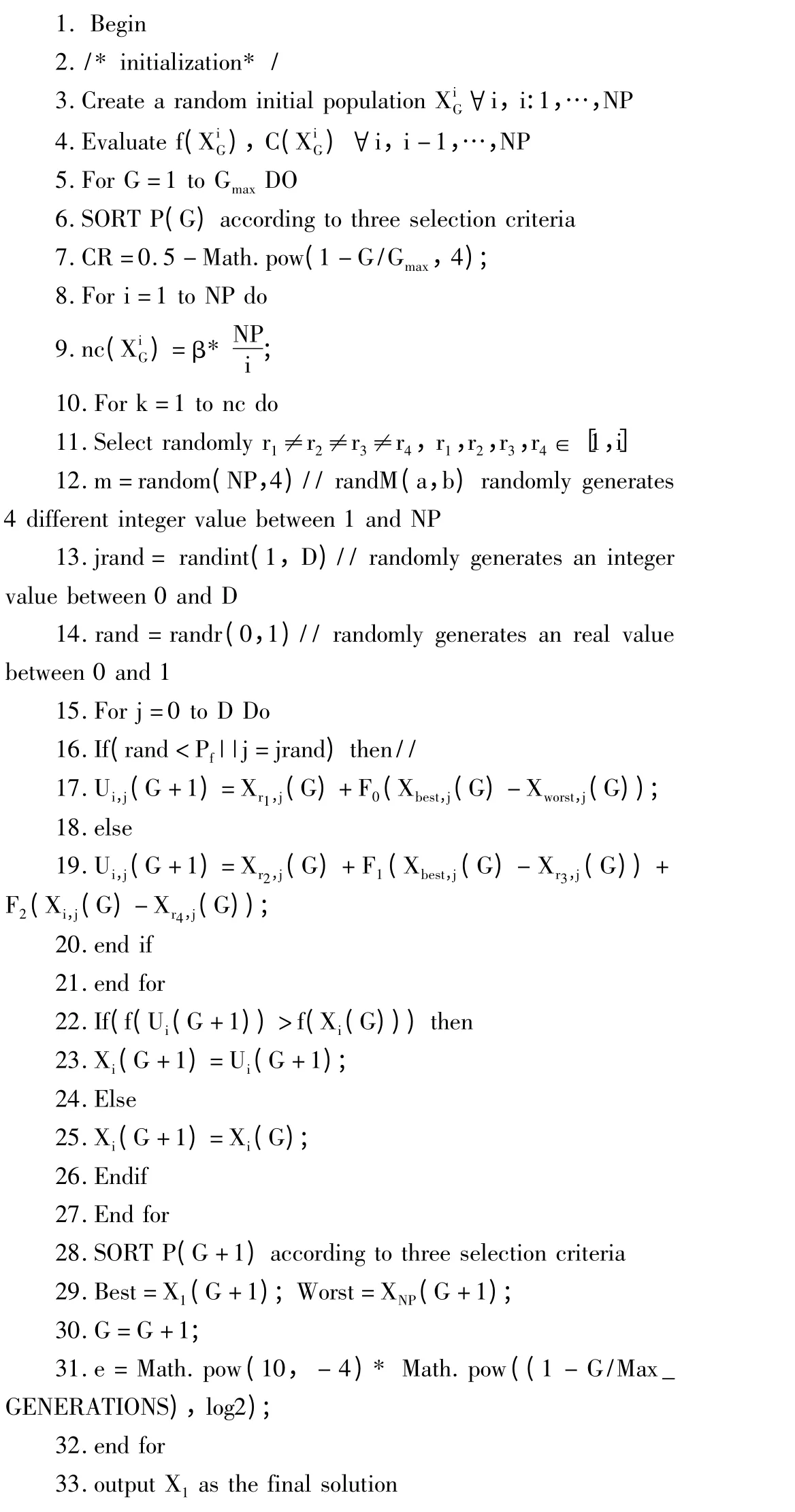
4 对比实验及结果分析

4.1 比较测试实验

CEC2006 中有24 个测试函数，函数g20 没有可行解，函数g22 很难找到可行解［9］，故本文算法重点对其余22 个测试函数进行测试，算法评估次数为5×104次，每个函数独立运行25 次，实验结果见表2，表2 中的性能指标包括最好结果、中间结果、平均结果、最差结果和解的标准方差，分别与COMDE 算法［9］作对比。1 表示本文算法(PLMIDE)，2 表示COMDE 算法。表2 中黑体为最优解。

表2 PLMIDE 算法(1)与COMDE 算法(2)实验结果对比

4.2 实验结果分析

实验数据验证了本文算法除了约束性很强的2个函数g20 和g22 以外，都成功地找到了最优解，对大部分函数效果非常好，求解精度也很高，特别是函数g3、g5、g7、g8、g10、g14、g15、g16、g18、g21、g23、g24取得了比笔者所了解到的最优解更优解，函数g2 因其目标函数维数较高且拓扑结构非常复杂可以用来考察进化算法的搜索能力［17］，从数据对比可以看出，本文算法确实比COMDE 算法有更好的搜索能力。从算法标准差对比中，本文算法普遍小于COMDE 算法，说明收敛精度更高，鲁棒性也更好。

5 结束语

本文提出了一种新的结合择优学习的混合变异策略和克隆策略的多个体差分算法，利用择优学习来实现对解空间的快速搜索，这种择优学习策略，具有快速找到可行解区域，且能够加快算法的收敛速度的能力。而使用克隆策略扩展搜索空间，可以使群体在最优解区域更加详尽地搜索，向最优解逼近，提高了算法的求解精度，通过实验验证，结果表明，本文算法在进化初期就能够快速定位到可行域中的最优解区域，后期通过克隆策略提高了求解精度，最终使得算法在求解效率和求解精度上都有较好表现，笔者下一步工作主要是研究其他搜索算法和约束处理技术用来提高本文算法的性能，以及尝试将本文算法扩展到求解多目标约束优化问题中。

［1］Storn R，Price K.Differential Evolution:A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces［R］.TR-95-012，Berkeley:University of California，1995.

［2］Mezura-Montes E，Velázquez-Reyes J，Coello Coello C A.Modified differential evolution for constrained optimization［C］// Proceedings of the 2006 IEEE Congress on Evolutionary Computation.2006:25-32.

［3］Brest J，Boškovi B，Zumer V.An improved self-adaptive differential evolution algorithm in single objective constrained real-parameter optimization［C］// Proceedings of the 2010 IEEE Congress on Evolutionary Computation.2010:1073-1080.

［4］Takahama T，Sakai S.Constrained optimization by the ε constrained differential evolution with an archive and gradient-based mutation［C］// Proceedings of the 2010 IEEE Congress on Evolutionary Computation.2010:1680-1688.

［5］Takahama T，Sakai S.Efficient constrained optimization by the ε constrained differential evolution with rough approximation using kernel regression［C］// Proceedings of the 2013 IEEE Congress on Evolutionary Computation.2013:1334-1341.

［6］Wang Yong，Cai Zixing，Zhang Qingfu.Differential evolution with composite trial vector generation strategies and control parameters［J］.IEEE Transactions on Evolutionary Computation，2011，15(1):55-66.

［7］Zou Dexuan，Liu Haikuan，Gao Liqun，et al.A novel modified differential evolution algorithm for constrained optimization problems［J］.Computers ＆ Mathematics with Applications，2011，61(6):1608-1623.

［8］郑建国，王翔，刘荣辉.求解约束优化问题εDE 算法［J］.软件学报，2012，23(9):2374-2387.

［9］Mohamed A W，Sabry H Z.Constrained optimization based on modified differential evolution algorithm［J］.Information Sciences，2012，194:171-208.

［10］Datta R，Deb K.Individual penalty based constraint handling using a hybrid bi-objective and penalty function approach［C］// Proceedings of the 2013 IEEE Congress on Evolutionary Computation.2013:2720-2727.

［11］Mezura-Montes E，Coello Coello C A.Constraint-handling in nature-inspired numerical optimization:Past，present and future［J］.Swarm and Evolutionary Computation，2011，1(4):173-194.

［12］Runarsson T P，Yao Xin.Search biases in constrained evolutionary optimization［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part C:Applications and Reviews，2005，35(2):233-243.

［13］Long Qiang.A constraint handling technique for constrained multi-objective genetic algorithm［J］.Swarm and Evolutionary Computation，2014，15:66-79.

［14］Takahama T，Sakai S.Constrained optimization by the ε constrained differential evolution with gradient-based mutation and feasible elites［C］// Proceedings of the 2006 IEEE Congress on Evolutionary Computation.2006:308-315.

［15］Cheng Ran，Jin Yaochu.A social learning particle swarm optimization algorithm for scalable optimization［J］.Information Sciences，2015，291:43-60.

［16］Mezura-Montes E，Velázquez-Reyes J，Coello Coello C A.A comparative study of differential evolution variants for global optimization［C］// Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation.2006:485-492.

［17］王勇，蔡自兴，周育人，等.约束优化进化算法［J］.软件学报，2009，20(1):11-29.