基于多核超限学习机的实时心电信号分析

秦兴彬颜 延樊建平王 磊

1（中国科学院计算技术研究所计算机应用研究中心 北京 100190）2（深圳市低成本健康重点实验室 深圳 518055）3（中国科学院深圳先进技术研究院 深圳 518055）

基于多核超限学习机的实时心电信号分析

秦兴彬1颜 延2，3樊建平3王 磊2，3

1（中国科学院计算技术研究所计算机应用研究中心 北京 100190）2（深圳市低成本健康重点实验室 深圳 518055）3（中国科学院深圳先进技术研究院 深圳 518055）

心电分类是一种复杂的模式识别问题。目前，大部分基于不同机器学习模型的心电分类方法都取得了很高的分类精度，但学习效率不高，因此需要一种快速的心电学习方法。文章提出了基于多种核函数的超限学习方法，利用不同的核函数将特征映射到希尔伯特空间，使心电数据在高维空间中线性可分，并在 MIT-BIH 标准库进行了该方法的实验验证。与其他方法相比，文章所提出的方法具有较高的分类准确率和更快的学习速度，对临床上动态心电图的检测与分析和个性化的实时心电监测具有重要意义。

核方法；超限学习机；心电监测；心电信号分类；实时分类

1 引 言

在过去三十年中，心电图（Electrocardiogram，ECG）分析已经成为热门的研究课题并为心脏疾病诊断提供了许多有价值的信息。随着心电图不断地为临床提供丰富的诊断信息，大量动态心电图已成为新的趋势。对大规模心电数据分析，最主要的是有效的特征提取和快速的心电分类。由于 ECG 信号不稳定的特点，小波变换已经被用来检测和过滤离散数据，提取有效的心电分类特征。同时，数字技术也可用于 ECG 信号分析和处理，主要包括时域和频域方法。

针对不同的心律失常的识别和分类，很多高精度的算法已经用于 ECG 信号的分析，主要包括：混合模糊神经网络（Fuzzy Neural Netwoks，FNNs）［1］、隐马尔可夫模型［2］、时域和频域的特征［3-5］、形态和动态特征［6-8］、支持向量机（Support Vector Machine，SVM）［9，10］、独立成分分析［11］、人工神经网络［12，13］和超限学习机（Extreme Learning Machine，ELM）［14］。其中，Andreao 等［2］首先采用了隐马尔科夫模型对心拍进行检测分割和分类：通过对波形建模和多通道的节拍分割和分类，达到对心电的单个波形进行划分。Zadeh 等［9］研究了正常的节拍和其他心脏疾病的室性早搏分类方法。通过去噪模块，波形的特征提取，以多种监督分类（多个不同层次和训练算法的多层感知器神经网络、不同粒度的支持向量机、径向基函数和概率神经网络）进行了研究，最终认为基于小波变换的特征具有最好的分类效果。Yu 等［11］提出了一种基于独立成分分析的集成方案和基于神经网络的心电分类方法。其中，独立成分分析用来将心电信号分解成独立的成分，统计独立成分的加权总和即是心电信号。最终这些成分的预测与 RR 间期，构成一个用于分类器的特征向量。而分类器则由两个神经网络组成，包括一个概率神经网络和一个反向传播神经网络。

以上这些算法大多依赖更好的特征选择，需要使用复杂的算法从 ECG 信号中提取。其中的一部分研究得到较好的分类结果，是因为使用了很多复杂的特征提取方法。虽然 FNNs 可以用来自动学习一些特征，但不适用于心率变化的心电信号。另外，大多数方法根据 ANSI/AAMI EC57标准将心跳分为五类，本文按 MIT 更精确的标准将心跳分为十二类。

对于动态心电图在临床应用，以及每天实时心脏功能监测或预警监控，开发快速的、自动化的算法或模型具有重要的意义。过去很多研究方法都集中在有监督的学习训练，而心电的标注数量有限，仅从少数的标注数据中很难得到很好的泛化模型。针对以上方法的缺陷，基于自编码、受限玻尔兹曼机［15］和基于聚类［16］的无监督方法成为新的研究方向。利用深度学习方法可以从大量的非标数据中自动学习心电特征，最后用少量的标注特征即可学习到一个高效的心电分类模型，但训练一个深度网络需要大量的时间。本文将用超限学习机［27，28］模型，通过高斯核函数和小波核函数将低维度的心电波形特征映射到高维空间中，极大地减少模型的训练时间，并且提高分类的精度。而 T-SNE［37］可以最大限度地保持低维的相似性矩阵和高维的相似性矩阵相近，因此采用该算法将高维心电向量降到低维空间。最终通过在低维空间中可视化，可以更好地说明分析结果。实验表明，基于核方法的超限学习机（k-ELM）在心电分类中具有高效性和实时性，嵌入 k-ELM 的心电监测和分析应用能够实现快速的心电学习和分类的目的。

2 心电数据库及类别

2.1 心电数据库

MIT-BIH 心律失常数据库［38］是最广泛使用的数据。在分类和检测算法的发展过程中，它被用作算法检测和测试分类的参考标准。实验采用MIT-BIH 心律失常数据库对所设计模型进行训练和评估。MIT-BIH 心律失常数据库包含 48 个记录，每条记录略超过 30 分钟，每个信号采样频率为 360 Hz。在大多数的记录中，第一个导联信号为肢体导 II（MLII），通过放置在胸部的电极获得；第二导联的信号是修改的 VI 导联（通常是 V2 或 V5，其中有一个实例是 V4 导联），电极也放置在胸部。大多数标签被放置在 R 波的峰值处，但手动插入标签不总是精确地放置在 R 波的峰值处，有时会有较小的误差偏移。另外，因为 102、104、107 和 217 四个记录中包含起搏心跳，不能反映心脏的自主活动过程，所以实验中除去这四个记录，最终共 44 个记录。

2.2 心电类别和标注

在 MIT-BIH 心律失常数据库中有 40 种标注种类。根据我们的统计，有十二标签在这 44个使用的记录中出现，所以心跳被分成 12 类：（1）NORMAL——正常搏动；（2）LBBB——左束支传导阻滞；（3）RBBB——右束支传导阻滞；（4）NESC——交界性逸搏；（5）AESC——心房逸搏；（6）ABERR——异常房性早搏；（7）NPC——交界性早搏；（8）APC——房性早搏；（9）VESC——室性逸搏；（10）PVC——室性早搏；（11）FLWAV——心室扑动波；（12）FUSION——心室融合心跳。详细的注解及相应的标签和映射标签见表1。

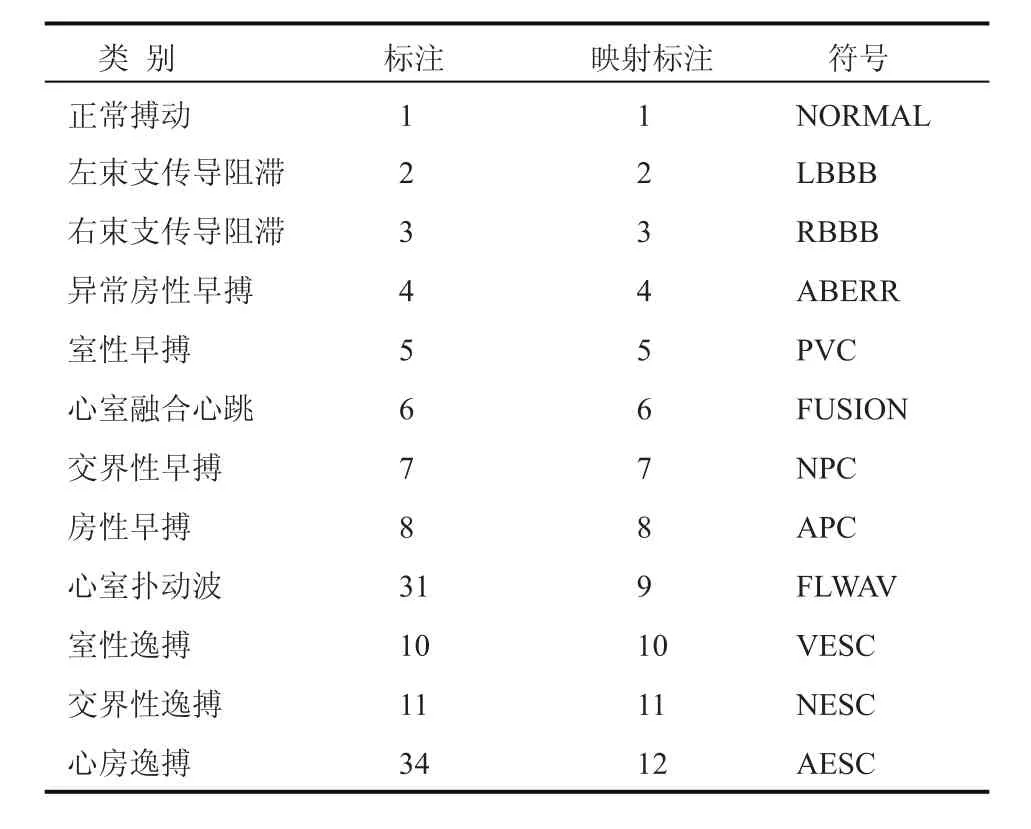
表1 MIT-BIH 心率失常类别Table 1 MIT-BIH arrhythmia classes

3 核方法

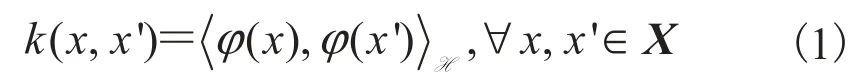
核方法的核心是采用非线性映射将原始数据由数据空间映射到特征空间，进而在特征空间中进行对应的线性操作。核方法是解决非线性模式分析问题的一种有效途径，但在多项式空间中直接进行内积运算将会引起“维数灾难”问题。为此，核方法通过某种非线性映射将原始特征空间映射到高维空间中，使其在高维空间中线性可分。相对于使用通用非线性学习器直接在原始数据上进行分析的范式，核方法有明显的优势：首先，通用非线性学习器不便于反应具体应用问题的特性，而核方法的非线性映射则是面向具体应用问题设计的，因此便于集成问题相关的先验知识；其次，与非线性学习器相比，线性学习器有更好的过拟合控制从而可以更好地保证泛化性能；最后，很重要的一点是核方法还是实现高效计算的途径，它能利用核函数将非线性映射隐含在线性学习器中进行同步计算而不需要在高维度的多项式空间中直接进行内积运算，使得计算复杂度与高维特征空间的维数无关。

4 超限学习机与核函数

4.1 超限学习机

超限学习机（ELM）［27，28］是一种单层前馈神经网络（Single-hidden-layer Feed-forward Networks，SLFNs），然后扩展到多种结构的 SLFNs，其中隐藏层可以是不同的神经元结构。在 ELM 中，隐藏层可以随机初始化产生，不需要进行调整。ELM 隐藏层的输出函数为：

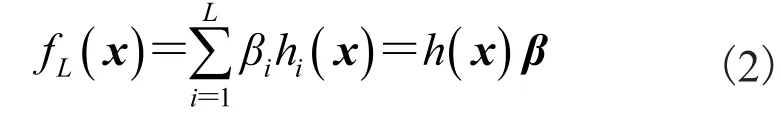
其中 H 为隐藏层的输出矩阵：

4.2 核超限学习机（k-ELM）

Suykens 等［39］将 SLFNs 的训练方法描述为：把 SLFNs 的隐藏层看做是 SVM 的特征映射，但和 SVM 不同的是，这里的隐藏层到输出层不需要调整，而是被作为一个优化问题来求解。SVM算法可以简单描述为：

其中，V 表示到隐藏层的连接矩阵；B 是偏移向量；γ 是正数常量；Q 是相应的 SVM 对偶问题的损失函数：

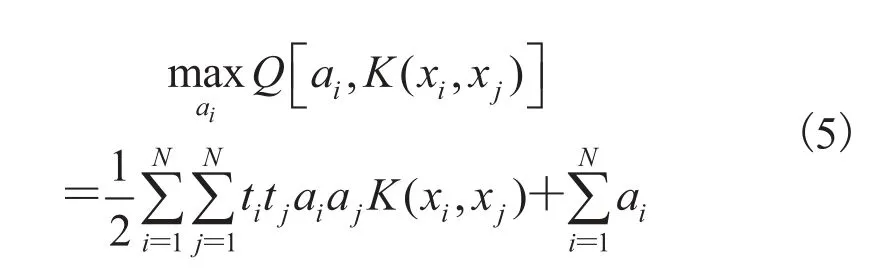
二次规划（Quadratic Programming，QP）的子问题需要求解隐藏层参数 V 和 B，而 ELM 的隐藏层是随机初始化的。

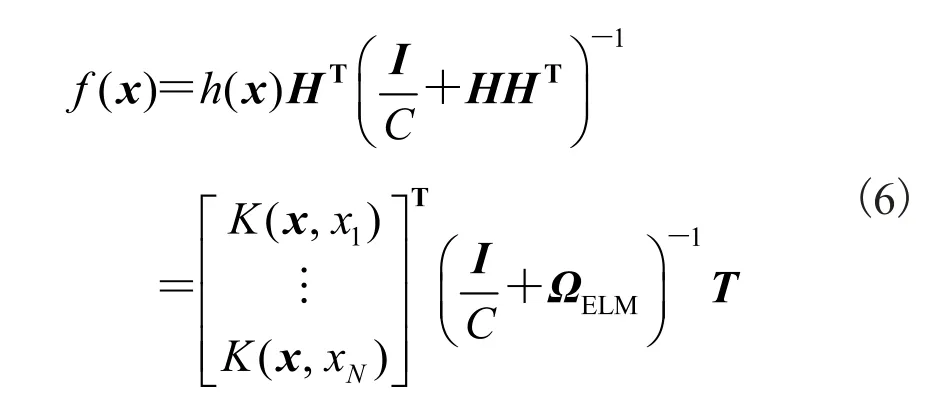
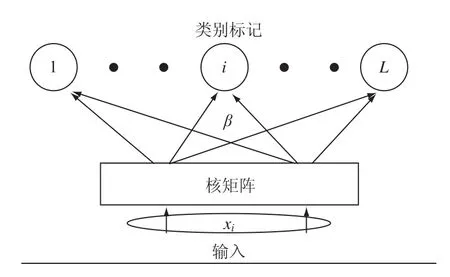
图1 k-ELM 结构Fig. 1 k-ELM structure

5 多核的超限心电识别与分类

5.1 ECG 预处理

心电信号的预处理过程主要包括两部分：心电数据滤波和心电信号分割。滤波器的任务是从ECG 信号中除去人工噪声的干扰。其中，人工噪声包括基线漂移、高频噪声干扰和电磁干扰。根据我们之前的研究，除了基线漂移干扰外，其他噪声对心电分类的精度影响较小，所以本次实验中仅仅去除心电信号中的基线偏移。

5.2 ECG 分割

本次实验使用 44 个记录，每个心电记录略超过 30 分钟，每个导联包含 650 000 个样本点。根据统计，每个心跳平均包含 277 个样本点。为了获得更多的信息，我们允许一部分重叠，将含有 340 个数据点长度定义一个窗口（其中 R 的峰值位于第 141 点上），分割结果如图 2 所示。考虑到心跳速率的变化，该窗口适于避免两个相邻心跳动的混合。ECG 的分割取决于 R 峰值检测，所以具有高精度局部最大值检测算法用于检测 R 峰。Mexican 小波［17］也是 R 峰值检测的一种高效的方法。

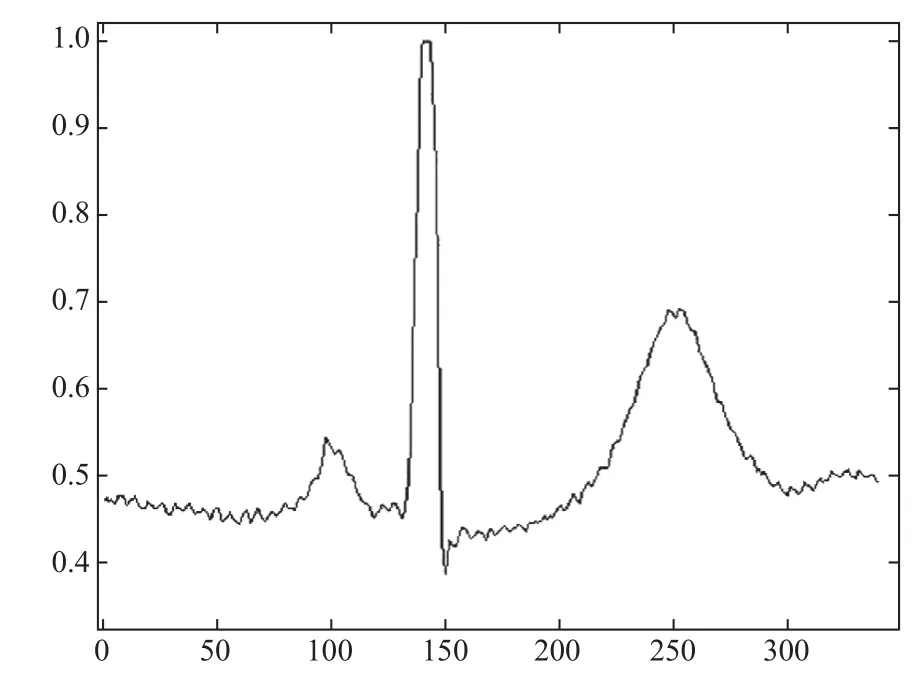
图2 单个心电波形Fig. 2 Single heartbeat wavelet

5.3 结果评估方法

用来评估心电信号分类标准的指标主要有：灵敏度 SNS，特异度 SPC 和整体精度 ACC。灵敏度是正常的心跳被分成正常类的概率：

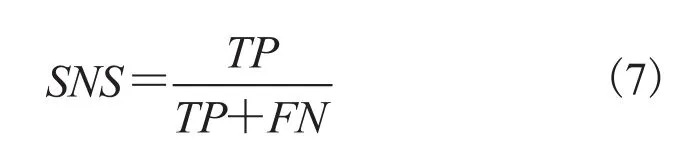
其中，TP（真阳性）为正确分类的正常心跳的数量；FN（假阴性）为正常的心跳被误分为其他类的心跳。

特异性是正确分类的异常心跳：

其中，FP（假阳性）为正确分类的异常心跳的数量；TN（真阴性）为被错误分类的异常心跳的数量。总体精度是正确分类的心跳概率：

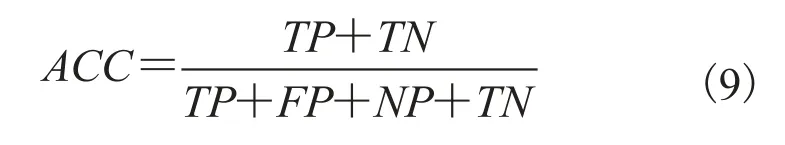
5.4 实验结果分析

实验中，心电的类型被分为 12 种（见表 1）。通过对心电数据的分割和向量化，使其适应超限学习机的结构，并采用不同的的核方法进行测试。MIT 心率失常数据库被分成两部分，其中50 485 个心跳的数据用于 k-ELM 的学习训练，剩余的 50 485 个的数据用于模型测试。

表2、表 3 分别为使用高斯核函数，小波核函数进行学习和分类的统计结果。结果显示，采用 5.3 中的评估方法，使用高斯核函数的灵敏度为 99.74%、特异性为 95.67%、正确率为98.67%，模型训练所用的时间为 796.3 秒，测试所用的时间为 43.4 秒；使用小波核函数的灵敏度为 99.76%、特异性为 96.04%、正确率为98.78%，模型训练所用的时间为 1 096.4 秒，测试所用的时间为 78.1 秒。虽然两种核函数对心电分类的精度都很高，但总体来看，小波核函数分类结果优于高斯核。

图3 为使用 T-SNE［37］算法将超限学习机的输出层可视化结果。从图 3 可以看出，使用核方法后，心电的可分性显著提升：相同类的标记变的更紧凑，不同类之间的距离增大，有较少的部分区域存在混合，波形的相似度较高，可分性较差。

图4 为参加训练样本点的个数与训练时间的关系结果（主机为 ThinkPad W530，cpu-Intel 酷睿i7394，16 G 内存）。从图 4 可以看出，训练时间随样本点的增多而快速增加。核矩阵的计算复杂度与样本点个数的平方成正比，因此基于核方法的超限学习受训练样本的制约，只适用于一定规模的训练样本个数。因此，接下来的研究需集中在矩阵的分解优化和分批的提升方法上，来解决样本数量的约束问题。

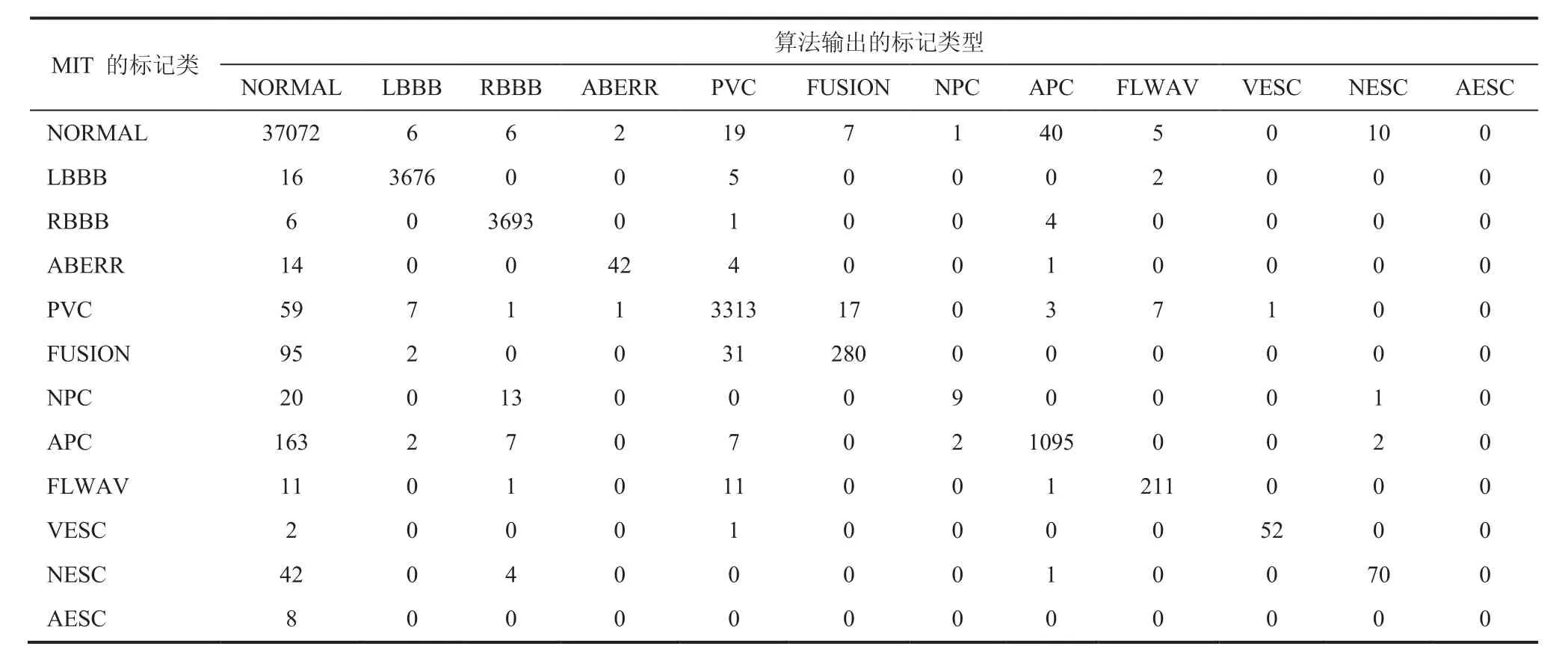
表2 使用高斯核函数的分类结果Table 2 The result of classifier using Gauss kernel function

5.5 与其他研究方法的比较

为了进一步分析文章所提出方法（k-ELM）的系统性能，选取了几个前人研究结果进行对比研究，结果见表 4。其中，深度网络［15］是我们之前用于心电特征自学习和分类的方法，采用受限玻尔兹曼机来构建的深度可靠网络，最大的优点就是能进行特征自编码，并且分类精度达到了98.83%，与本文提出的核超限学习方法结果比较相近。但训练一个高精度的深度网络需要 2 小时以上，而小波核超限学习方法仅需要 1 096.4秒。Andreao 等［2］用隐马尔科夫模型对单个心跳的 P、QRS、T 等波形进行建模，能对连续的时域心电信号进行分析。其主要优势在于对不同波形的识别准确率较高，局限在于不能进行复杂的波形识别，并且只能是对正常心跳和某些波形缺失异常进行二分类处理，正确率仅为 96.06%。本文对 12 种心跳类型进行分析，正确率高于这种方法。Banerjee 等［3］使用正交小波变换的方法进行特征提取，通过计算单个波形与标准模板的差异系统进行分类，这种方法的优点在于计算简单，但对噪声和心率变化的数据很敏感。Tadejko［4］使用自组织映射和支持向量机的信号特征分析和聚类方法进行形态特性分析，正确率97.82%，但是分类结果对特征提取的依赖性较大。这两种方法的分类精度都低于本文提出的方法。而 Ye 等［7］采用支持向量机的研究中，因剔除了 2 054 个难识别的特殊心跳样本（占 2.4% 的比例），所以结果正确率很高。

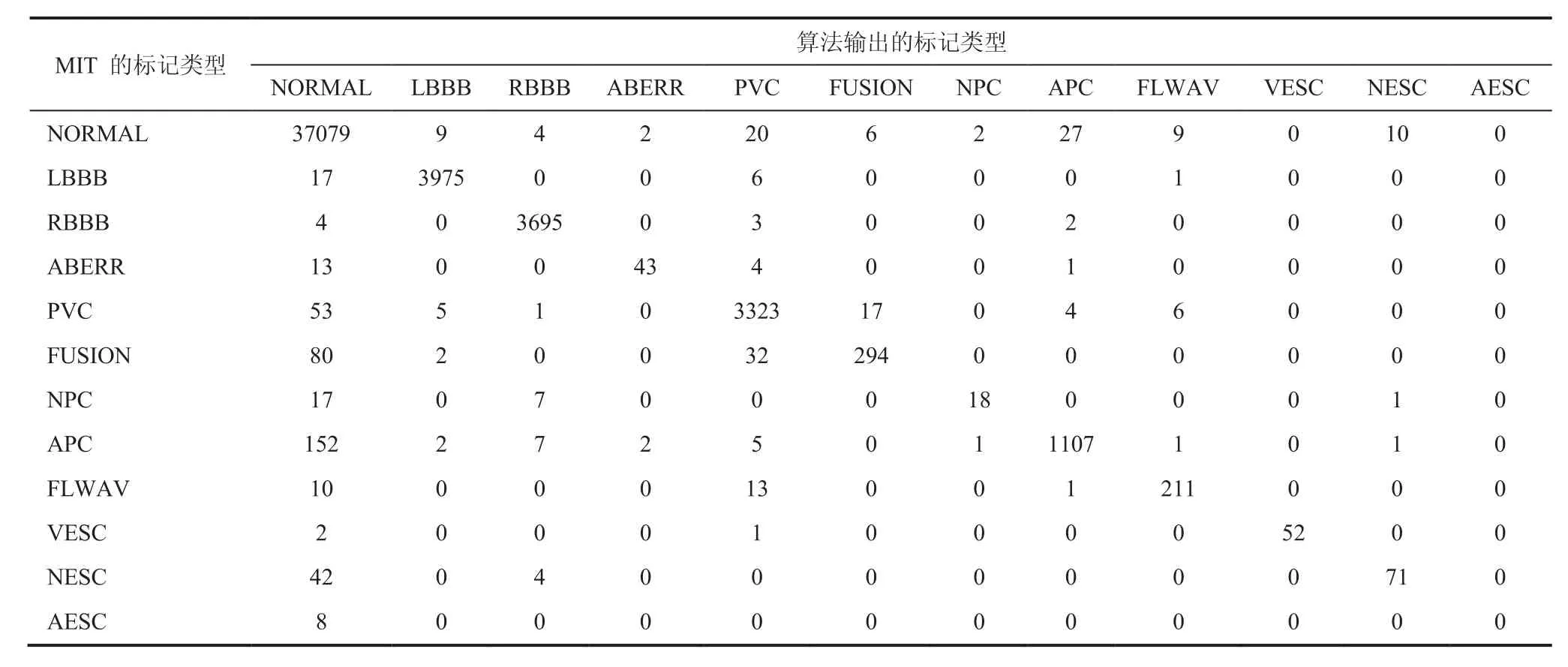
表3 使用小波核函数的分类结果Table 3 The result of classifier using wavelet kernel function

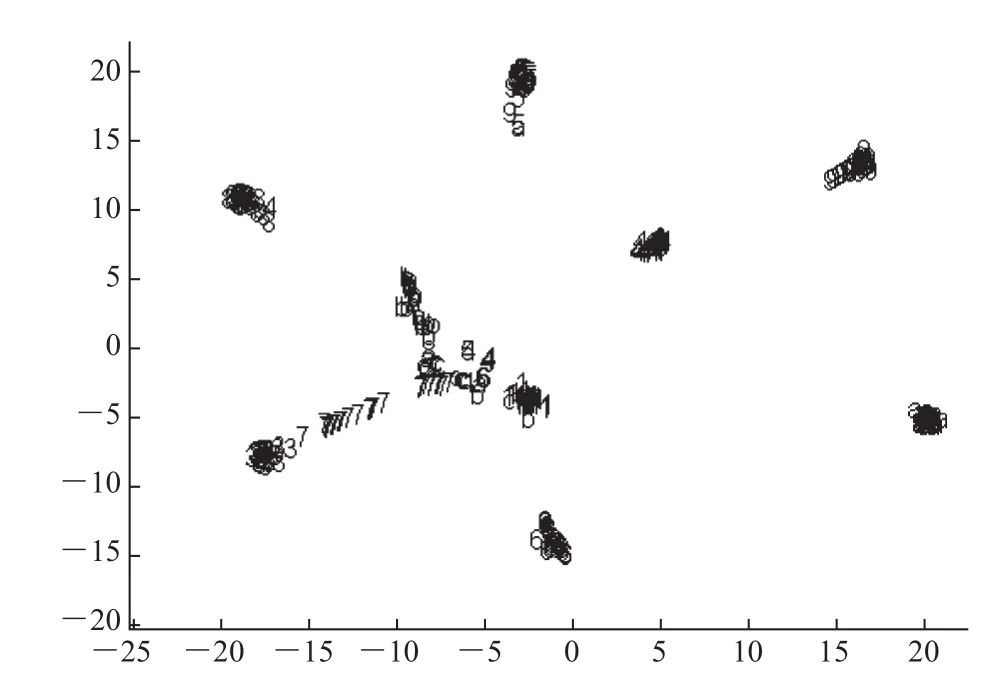
图3 超限学习机输出分布Fig. 3 The distribution of extreme learning machine output

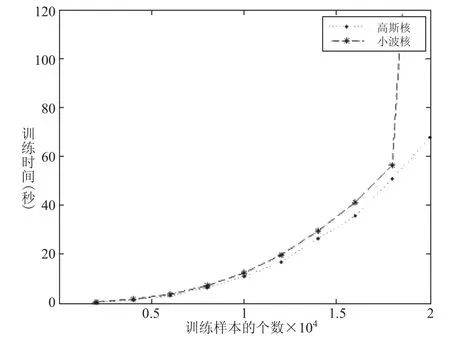
图4 模型学习时间与训练样本数Fig. 4 The relation between the number of training samples and learning time of the model

以上这些算法大多依赖于一些复杂的特征提取方法，因此分类器的好坏主要取决于选取的特征。深度网络可以通过自编码实现特征学习，不需要手动提取参数，我们的研究表明深度学习方法能通过原始的心电信号来实现高精度的分类。但是，所有的这些方法都需要大量的训练时间，尤其构造一个深度网络花费的时间更多。从图 4可以看出模型的训练时间与样本个数相关：一千以内的样本个数训练时间少于一秒，两万个样本训练仅需要一分钟左右，而深度网络训练时间需要几个小时。其他方法，如训练 SVM，当样本量较少时，能较快收敛；但当样本量较大时，收敛较慢且误差会增大。模型训练之前需要复杂的特征提取过程而在进行分类时也需要先提取特征，因而效率不高。通过基于核方法的超限学习机可以直接对原波形进行映射和分类，对 50 485 个样本进行分类时仅需要 78.1 秒。从表 4 的对比也可以看出，本文提出的 k-ELM 分类方法的正确率与深度网络相似，且比其他的一些研究方法的准确度高。因此，本文所提出的方法具有较高的准确率并且能进行快速地心电学习和分类。

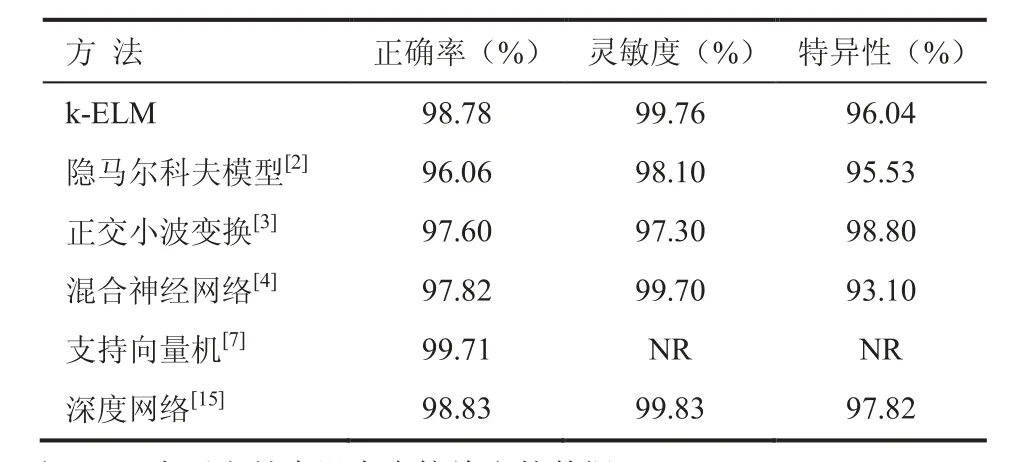
表4 与其他研究的比较Table 4 Compare with others work

6 小 结

心电图反应心脏活动的电生理信号，对心脏的功能分析和疾病的诊断具有重要参考价值。自动化心电图分类是长期临床监测必不可少辅助方法，尤其是应对一些突发性的疾病时，快速和精确的心电异常识别能够提供及时的预警。超限学习机能够进行快速的学习和分类，输出权值的求解不需要进行迭代，且最主要的是根据超限学习机的理论，可以使用多种核方法，将特征映射到高维空间中，使数据在高纬空间中线性可分。本文基于高斯核和小波核函数的超限学习方法，研究实时高效的心电学习与分类方法。使用这两种核方法都能够实现高准确率的心电分类。使用 MIT-BIH 心律失常数据库，测试了 50 485 个样本，最高分类精度达到了 98.78%，灵敏度为99.76%，特异性为 96.04%。对心电数据只进行了基线漂移校正，说明基于核方法的超限学习方法对心电数据分类具有很好的鲁棒性。同时，核函数避免了“维数灾难”，提高了分类的精度，从算法的训练时间来看，基于核方法的超限心电分类具有较快的学习和分类速度，适用于嵌入各种实时心电监测和分析的应用中。

［1］ Osowski S， Linh TH. ECG beat recognition using fuzzy hybrid neural network ［J］. IEEE Transactions on Biomedical Engineering， 2001， 48（11）： 1265-1271.

［2］ Andreao RV， Dorizzi B， Boudy J. ECG signal analysis through hidden markov models ［J］. IEEE Transactions on Biomedical Engineering， 2006， 53（8）： 1541-1549.

［3］ Banerjee S， Mitra M. Application of cross wavelet transform for ECG pattern analysis and classification ［J］. IEEE Transactions on Instrumentation and Measurement，2014， 63（2）： 326-333.

［4］ Tadejko P， Rakowski W. Hybrid wavelet-mathematical morphology feature extraction for heartbeat classification ［C］ // The International Conference on Computer as a Tool， 2007： 127-132.

［5］ Palreddy S， Tompkins WJ， Hu YH. Customization of ECG beat classifiers developed using SOM and LVQ ［C］ // IEEE 17th Annual Conference on Engineering in Medicine and Biology Society， 1995， 1： 813-814.

［6］ Mar T， Zaunseder S， Martinez J， et al. Optimization of ECG classification by means of feature selection ［J］. IEEE Transactions on Biomedical Engineering， 2011，58（8）： 2168-2177.

［7］ Ye C， Kumar BVKV， Coimbra MT. Heartbeat classification using morphological and dynamic features of ECG signals ［J］. IEEE Transactions on Biomedical Engineering， 2012， 59（10）： 2930-2941.

［8］ Philip DC， Dwyer MO， Reilly RB. Automatic classification of heartbeats using ECG morphology and heartbeat interval features ［J］. IEEE Transactions on Biomedical Engineering， 2004， 51（7）： 1196-1206.

［9］ Zadeh AE， Khazaee A， Ranaee V. Classification of the electrocardiogram signals using supervised classifiers and efficient features ［J］. Computer Methods and Programs in Biomedicine， 2010， 99（12）： 179-194.

［10］ Song MH， Lee J， Cho SP， et al. Support vector machine based arrhythmia classification using reduced features ［J］. International Journal of Control， Automation， and Systems， 2005， 3（4）： 571-579.

［11］ Yu SN， Chou KT. Integration of independent component analysis and neural networks for ECG beat classification ［J］. Expert Systems with Applications， 2008， 34（4）：2841-2846.

［12］ Hu YH， Tompkins WJ， Urrusti JL， et al. Applications of artificial neural networks for ECG signal detection and classification ［J］. Journal of Eletrocardiology， 1993， 26：66-73.

［13］ Prasad GK， Sahambi JS. Classification of ECG arrhythmias using multiresolution analysis and neural networks ［C］ // Conference on Convergent Technologies for the Asia-Pacific Region， 2003， 1： 227-231.

［14］ Karpagachelvi S， Arthanari M， Sivakumar M. Classification of ECG signals using extreme learning machine ［J］. Computer and Information Sciences， 2011，4（1）： 42-52.

［15］ Yan Y， Qin XB， Fan JP， et al. An optimization algorithm of multilead electrocardiography classification using restricted Boltzmann machine ［C］ // The 12th International Conference on Wearable and Implantable Body Sensor Networks， 2014.

［16］ Gezer BL， Kuntalp D， Kuntalp M. Clustering of arrhythmic ECG beats using morphological properties and windowed raw ECG data ［C］ // IEEE 19th Conference on Signal Processing and Communications Applications（SIU）， 2011： 738-741.

［17］ Burke MJ， Nasor M. ECG analysis using the Mexican-Hat wavelet ［C］ // Proceedings of the WSES International Conference on Multirate Systems & Wavelet Analysis，2001： 3531-3536.

［18］ Afonso VX， Tompkins WJ， Nguyen TQ， et al. ECG beat detection using filter banks ［J］. IEEE Transactions on Biomedical Engineering， 1999， 46（2）： 192-202.

［19］ Clifford GD， Azuaje F， McSharry P. Advanced Methods And Tools for ECG Data Analysis ［M］. Norwood， MA，USA： Artech House， Inc.， 2006.

［20］ Kundu M， Nasipuri M， Basu DK. A knowledge-based approach to ECG interpretation using fuzzy logic ［J］. IEEE Transactions on Systems， Man， and Cybernetics，Part B： Cybernetics， 1998， 28（2）： 237-243.

［21］ Moavenian M， Khorrami H. A qualitative comparison of artificial neural networks and support vector machines in ECG arrhythmias classification ［J］. Expert Systems with Applications， 2010， 37（4）： 3088-3093.

［22］ Chudacek V， Petrik M， Georgoulas G， et al. Comparison of seven approaches for holter ECG clustering and classification ［C］ // The 29th Annual InternationalConference of the IEEE， Engineering in Medicine and Biology Society， 2007： 3844-3847.

［23］ Jiang W， Kong SG. Block-based neural networks for personalized ECG signal classification ［J］. IEEE Transactions on Neural Networks， 2007， 18（6）： 1750-1761.

［24］ Lin CW， Yang YTC， Wang JS， et al. A wearable sensor module with a neural-network-based activity classification algorithm for daily energy expenditure estimation ［J］. IEEE Transactions on Information Technology in Biomedicine， 2012， 16（5）： 991-998.

［25］ Ölmez T. Classification of ECG waveforms by using RCE neural network and genetic algorithms ［J］. Electronics Letters， 1997， 33（18）： 1561-1562.

［26］ Melgani F， Bazi Y. Classification of electrocardiogram signals with support vector machines and particle swarm optimization ［J］. IEEE Transactions on Information Technology in Biomedicine， 2008， 12（5）： 667-677.

［27］ Huang GB， Zhu QY， Siew CK. Extreme learning machine： Theory and applications ［J］. Neurocomputing，2006， 70（1-3）： 489-501.

［28］ Huang GB， Zhou HM， Ding XJ， et al. Extreme learning machine for regression and multiclass classification ［J］. IEEE Transactions on Systems， Man and Cybernetics-Part B： Cybernetics， 2012， 42（2）： 513-529.

［29］ Huang GB， Liang NY， Rong HJ， et al. On-line sequential extreme learning machine ［J］. Computational Intelligence， 2005， 2005： 232-237.

［30］ He Q， Shang TF， Zhuang FZ， et al. Parallel extreme learning machine for regression based on MapReduce ［J］. Neurocomputing， 2013， 102： 52-58.

［31］ Huang GB， Ding XJ， Zhou HM. Optimization method based extreme learning machine for classification ［J］. Neurocomputing， 2010， 74（1-3）： 155-163.

［32］ Cao JW， Lin ZP， Huang GB. Composite function wavelet neural networks with extreme learning machine ［J］. Neurocomputing， 2010， 73（7-9）： 1405-1416.

［33］ Huang G， Huang GB， Song SJ， et al. Trends in extreme learning machines： a review ［J］. Neural Network， 2015，61： 32-48.

［34］ Wang XL， Gui Q， Liu BW， et al. Enabling smart personalized healthcare： a hybrid mobile-cloud approach for ECG telemonitoring ［J］. IEEE Journal of Biomedical and Health Informatics， 2014， 18（3）： 739-745.

［35］ Xia HN， Asif I， Zhao XP. Cloud-ECG for real time ECG monitoring and analysis ［J］. Computer Methods and Programs in Biomedicine， 2013， 110（3）： 253-259.

［36］ Basheer IA， Hajmeer M. Artificial neural network：fundamentals， computing，design and application ［J］. Journal of Microbiological Methods， 2000， 43（1）：3-31.

［37］ Laurens VDM， Hinton G. Visualizing high-dimensional data using t-SNE ［J］. Journal of Machine Learning Research， 2008， 9（11）： 2579-2605.

［38］ Goldberger AL， Amaral LAN， Glass L， et al. Physiobank，physiotoolkit，and physionet：components of a new research resource for complex physiologic signals ［J］. Circulation， 2000， 101（23）： e215-e220.

［39］ Suykens JAK， Vandewalle J. Training multilayer perceptron classifiers based on a modified support vector method ［J］. IEEE Transactions on Neural Networks，1999， 10（4）： 907-911.

Real-Time Electrocardiogram Analysis Based on Multi-Kernel Extreme Learning Machine

QIN Xingbin1YAN Yan2，3FAN Jianping3WANG Lei2，3
1（ Computer Application Research Center， Institute of Computing Technology， Chinese Academy of Sciences， Beijing 100190， China ）2（ The Shenzhen Key Laboratory for Low-cost Healthcare， Shenzhen 518055， China ）3（ Shenzhen Institutes of Advanced Technology， Chinese Academy of Sciences， Shenzhen 518055， China ）

Electrocardiogram（ECG） classification is a complex pattern recognition problem. At present， most of the ECG classification methods based on different machine learning model had achieved a high classification accuracy， but the learning efficiency was low. Therefore， a fast ECG learning algorithm was necessary. In this paper， a method of extreme learning machine was presented， which mapped the original feature space into Hilbert space with different kernel functions and made the ECG date in high dimensional space linearly separable. At last， the experimental verification was carried on MIT-BIH standard library. The results show that the proposed method has higher accuracy and faster learning speed than existing methods， which may be a potential tool for detection and analysis of clinical dynamic electrocardiogram and personalized real-time ECG monitoring.

kernel method； extreme learning machine； electrocardiogram monitoring； electrocardiogram analysis； real-time classification

TP 391.6

A

2015-05-13

2015-07-05

国家 863 项目（2012AA02A604）；国家下一代通信技术重点工程（2013ZX03005013）；广东省创新团队（2011S013）

秦兴彬，硕士，研究方向为半监督学习方法和心电大数据分析；颜延，博士，研究方向为机器学习和健康大数据；樊建平，研究员，研究方向为高性能计算、云计算和分布式计算；王磊（通讯作者），研究员，研究方向为人体传感器网络、健康感知和医学芯片，E-mail：wang.lei@siat.ac.cn。