时频分析方法及其在火箭振动数据分析中的应用

张建海，韩迎春，曾艳艳，吴功友，李连周

（1.宇航动力学国家重点实验室，西安710043；2.中国西安卫星测控中心，西安710043）

时频分析方法及其在火箭振动数据分析中的应用

张建海1，2，韩迎春1，2，曾艳艳2，吴功友1，李连周2

（1.宇航动力学国家重点实验室，西安710043；2.中国西安卫星测控中心，西安710043）

为了对火箭振动数据进行精确的时频分析，给火箭改进设计、性能分析提供重要依据，研究了几种典型的时频分析方法及各自的原理、特点，并进行算法仿真；结合火箭振动数据特点建立算法模型，对实测数据进行时频分析，结果对比表明：希尔伯特-黄变换（Hilbert-Huang Transform，HHT）时频分析方法具有很强的自适应特性，其时频谱具有最佳的时频分辨率，是优良的火箭振动数据时频分析方法。

时频分析；HHT变换；非平稳信号

长期以来，对火箭振动数据的分析所采用的是傅立叶变换分析方法，将数据从时域转换到频域，得到振动数据在频域的概观特性。对于火箭研制部门来说，非常关心火箭飞行特征时刻信号，即非平稳特征信号。傅立叶分析存在时域与频域的局部化矛盾，得到信号频率信息的同时时间信息将全部损失，无法很好地为我们揭示非平稳特征，不能直观描述信号的频率、能量随时间变化的情况，已经不能满足火箭改进设计、性能分析、故障诊断等工作需要，成为火箭数据高精度处理急需解决的技术难题［1］。

近年来，时频分析方法作为非平稳信号处理的一个重要分支，已得到很大的发展，该方法克服传统傅立叶变换的这种全局性变化的局限性，对于非平稳信号通过变换处理，使待分析信号的特征信息尽可能地突显出来。诸多学者已经研究并提出了多种有效的时频分析方法，其时频分辨率和聚集性各不相同，典型的时频分析方法主要有短时傅里叶变换、小波变换、魏格纳-威力分布和希尔伯特-黄变化等。

1 典型时频分析方法仿真对比研究

仿真信号如式（1）所示：

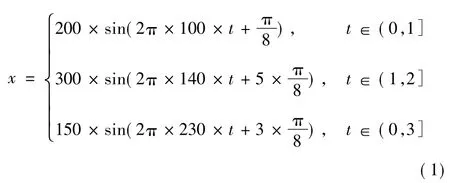
该信号在1 s、2 s处发生明显的频率与幅值跳变，每段间隔的信号均为恒定频率的正弦波，3段信号频率分别为100 Hz、140 Hz、230 Hz，采样率fs=1 000，共3 000个数据点，图1（a）为时域信号曲线，图1（b）为其快速傅里叶谱。从图1（b）可以明显看出信号包含100 Hz、140 Hz、230 Hz 3个频率，但存在频率泄露，且无法得知这些频率随时间变化的情况。

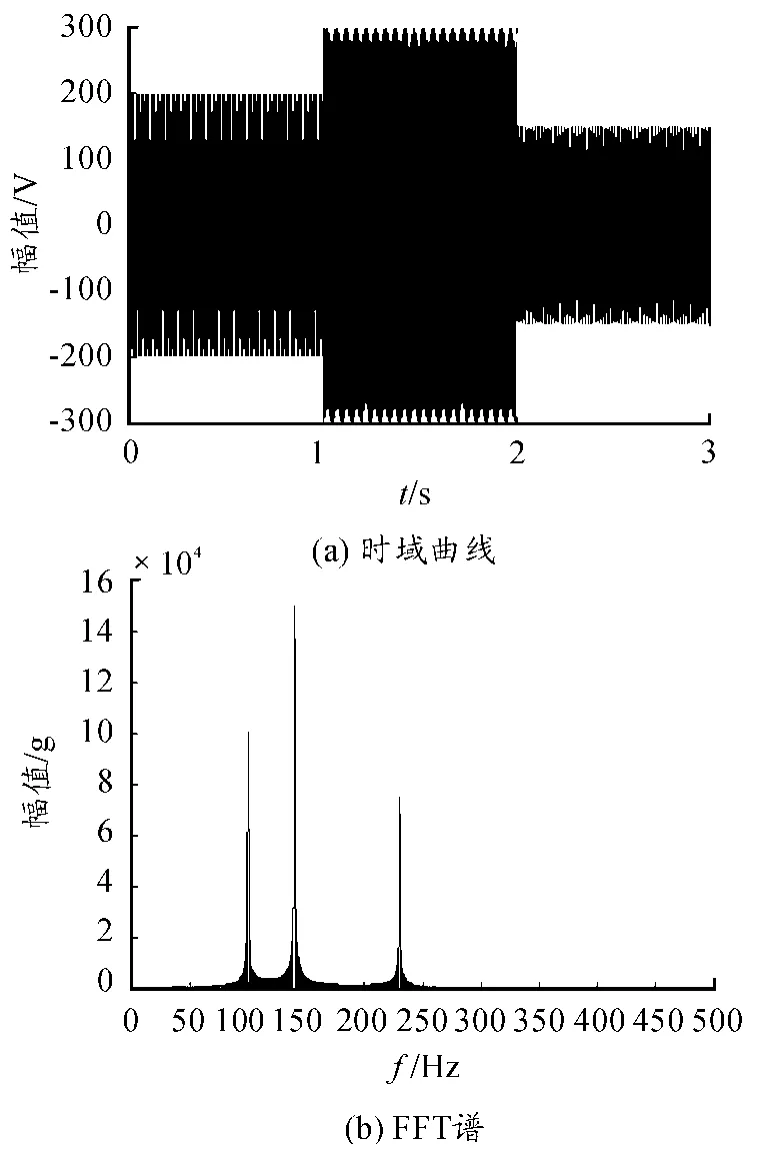
图1 仿真信号的时域曲线及其FFT谱

1.1 短时傅立叶变换方法

短时傅里叶变换（Short Time Fourier Transform，STFT）是和傅里叶变换相关的一种数学变换，用以确定时变信号其局部区域正弦波的频率。给定一个时间宽度很短的窗函数，假定分析窗函数h（t）在一个短时间间隔内是平稳（伪平稳）的，移动窗函数，则信号x（t）的短时傅里叶变换定义为

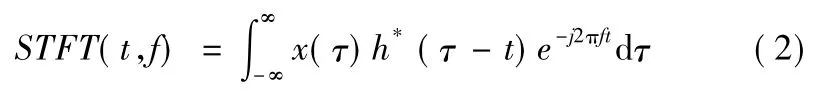
对于给定的时间t，STFT（t，f）可看作是该时刻的频谱，它的时间分量对应于窗口在平移过程中其中心所处的各个位置。

STFT概念直接，算法简单，已经成为研究非平稳信号十分有力的工具。同时STFT有两个主要困难是无法克服的：一是窗函数的选择问题。分析包含两个分量以上的信号，在选取窗函数时就会感到困难，很难使一个窗同时满足几种不同的要求；二是对于窗函数长度的选择问题，窗函数的长度与频谱图的频率分辨率有直接的联系［2］。

针对仿真信号加矩形窗进行短时傅里叶变化，时频谱如图2（a）所示。它较好地描述了三个频率分量在采样区间内的频率变化特征，由于STFT的先天性缺陷，这三个频率分量在跳变时刻有频率重叠的现象。

1.2 魏格纳-威力分布方法

魏格纳-威力分布（Winger-Ville Distribution，WVD）是一种最基本也是应用非常多的时频分析方法，它直接用信号的时频二维分布描述非平稳信号幅频特性随时间的变化情况。

连续时间复信号x（t），t∈R，则该信号的WVD表示为：

式（5）中：h（t）是观测信号x（t）的解析信号；h*（t）是h（t）的共轭。

如果h（t）=h1（t）+h2（t），则有：

由于WVD分布不是线性的，即两信号之和的WVD分布并非每一个信号的WVD分布之和，其中多出一个附加项，即交叉项，这影响了WVD分布的直观表示。为降低和消除WVD分布带来的交叉干扰除，可采取对WVD分布结果在时域和频域作平滑的方法，这包括伪WVD分布和平滑伪WVD分布［3，4］。

图2（b）为该仿真信号的WVD分布时频图，由于交叉项干扰，在1 s和2 s左右分别出现了120 Hz和185 Hz的虚假频率，影响对信号频率成分的正确判断。

1.3 小波变换方法

小波分析是一种时间-尺度分析方法，介于纯时间域的方波分析和纯频率域的傅立叶分析之间，同时具有时间域和频率域的良好局部化性质。不同频率成份在时域上的取样步长具有调节性，高频者小，低频者大［5，6］。

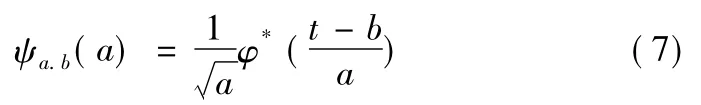
式（7）中：a为伸缩尺度；b为平移参数，函数ψ（t）为小波母函数。

连续小波变换能够在信号高频段提供较高的时间分辨率，在信号低频段提供较高的频率分辨率，具有短时傅立叶变换不可比拟的优点，但是由于尺度因子a与频率f没有直接的联系，而且在小波变换中没有明显表现出来，因此小波变换的结果不是一种真正的时频谱。

图2（c）为仿真信号的Morlet小波谱，三个频率分量被较好的分辨出来，但是频率分辨率都要差一些。

1.4 希尔伯特-黄变换方法

希尔伯特-黄变换（Hilbert Huang Transform，HHT）是由美国国家宇航局的N.E.Huang提出的一种称信号解析方法，从本质上讲，该方法是对信号进行平稳化处理。HHT方法主要由经验模态分解（Empirical Mode Decomposition，EMD）和Hilbert谱分析（Hilbert Spectrum Analyze，HSA）两部分组成。

1）EMD分解：将信号中真实存在的不同尺度波动或趋势逐级分解出来，产生有限个具有不同特征尺度的数据序列，即固有模态函数（Intrinsic Mode Function，IMF）。原始信号h（t）经过EMD分解后，可表示为n阶固有模态函数和一个残余项rn（t）的和：

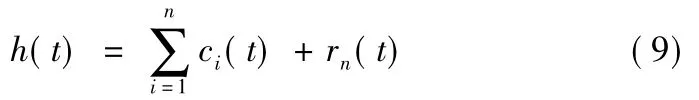
其中ci（t）为IMF分量，残余信号rn（t）的值非常小，小于预定的误差，一般为单调函数，参考文献［7］给出了详细的分解过程。

2）Hilbert谱分析：对EMD分解得到的每个IMF分量作Hilbert变换，从而得到Hilbert时频谱和Hilbert边际谱，即得到瞬时频率和能量。

首先对每个分量ci（t）作希尔伯特变换得到：

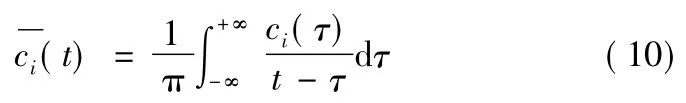
再构造解析信号：

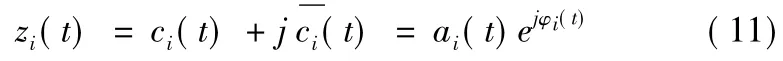
计算幅值函数和相位函数：

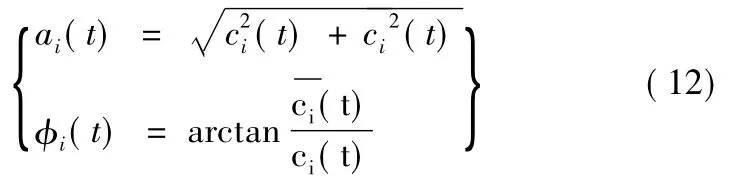
瞬时频率：

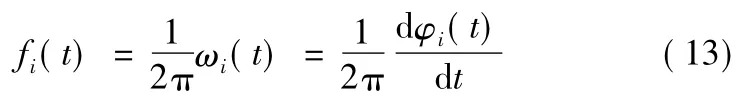
Hilbert时频谱表示为

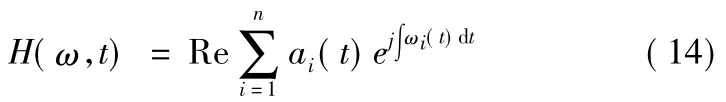
EMD分解无需选择基函数，按频率从高至低的顺序进行分解，获得的IMF分量大都具有物理意义。EMD分解依据信号本身的固有特性进行分解，是一种自适应强和分解高效的方法，Hilbert谱具有更好的局部化能力，Hilbert能量谱清晰而详细地显示了能量随时频变化的具体分布，瞬时能量谱更直观地表明了能量的集中区间［8］。

该方法虽然是处理非平稳、非线性信号的得力途径，但是也存在一定的缺陷，如果不能很好的解决这些缺陷，可能会使分析结果受到影响或失效。近年来，经过众多学者对该方法的深入研究，算法也得到了不断的发展完善。文献［9-12］提出了噪声去除标准、模态混叠解决方案和抑制端点效应等方法，较好的解决了该方法的先天性缺陷问题。

利用波形匹配法对仿真信号两端各延拓10个点，再进行EMD分解和HHT变换，然后抛弃延拓的数据点，得到图2（d）的HHT时频谱。从图2（d）可以明显看出3个频率在跳变时刻频率成分没有重叠，也无交叉项干扰，时间分辨率和频率分辨率均非常高。

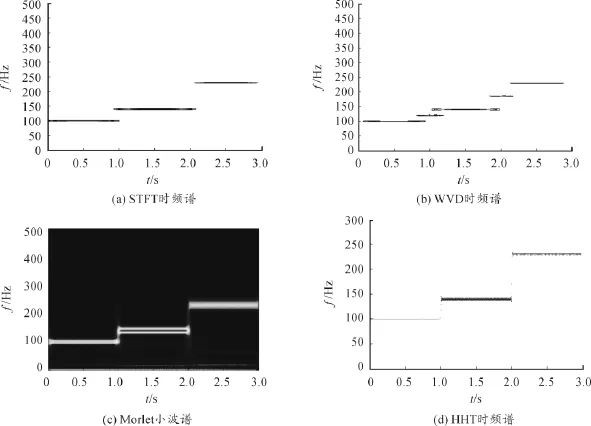
图2 仿真信号的STFT、WVD、Wavelet及HHT谱

图3为HHT变换的三维空间谱，清晰地描述了信号频率-时间-能量的变化情况。

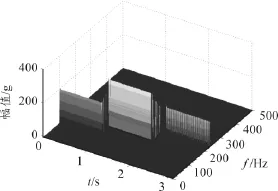
图3 HHT三维空间谱

2 火箭振动数据时频分析算法应用

对某型号火箭实测振动数据信号进行分析处理，选取时间段为火箭飞行特征段，该段数据是标准的非平稳信号，共1 024个数据点，图4（a）为时域曲线，图4（b）为FFT谱分析结果，从图4（b）可以看出存在着27 Hz和130 Hz的振动频率，但不能确定振动频率出现的时刻。

图5（a）为采用8点矩形窗的短时傅里叶变换，较好的描述了这两个频率的分布情况。图5（b）为Morlet小波谱。图5（c）为WVD分布图，把该图与图4（b）和图5（a）进行比较，不难发现WVD分布存在交叉项干扰。

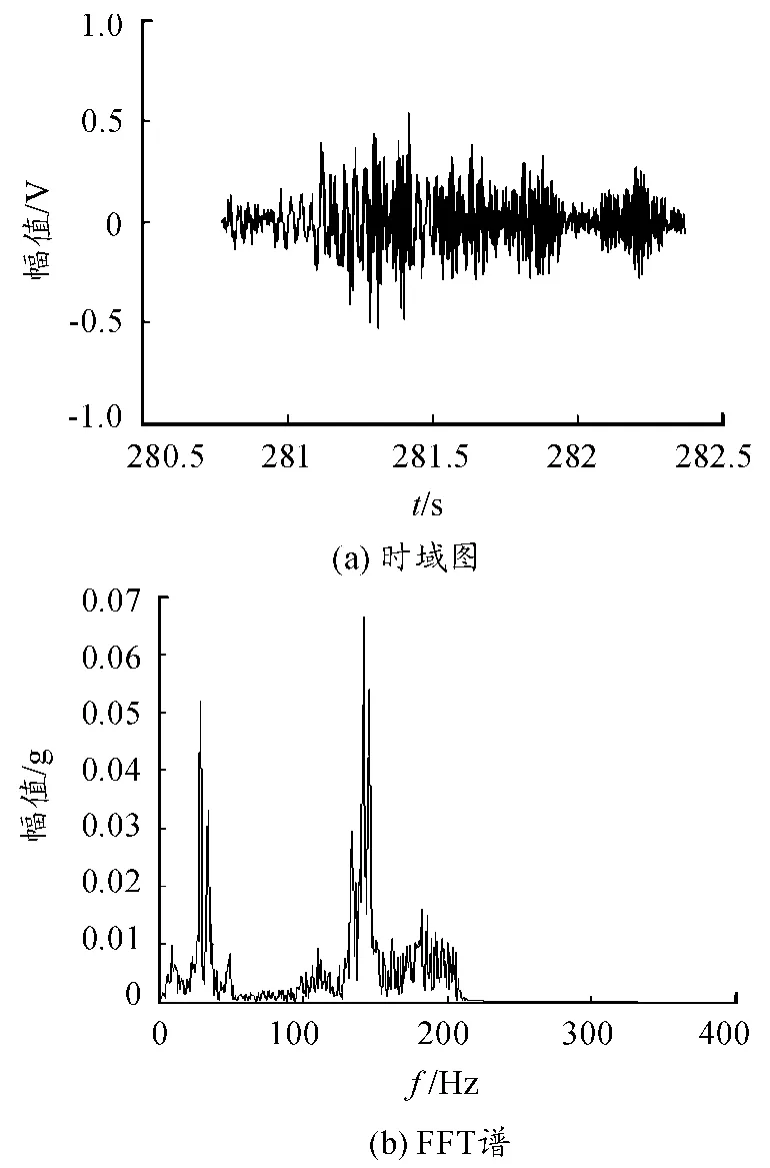
图4 实测信号时域曲线及其FFT谱

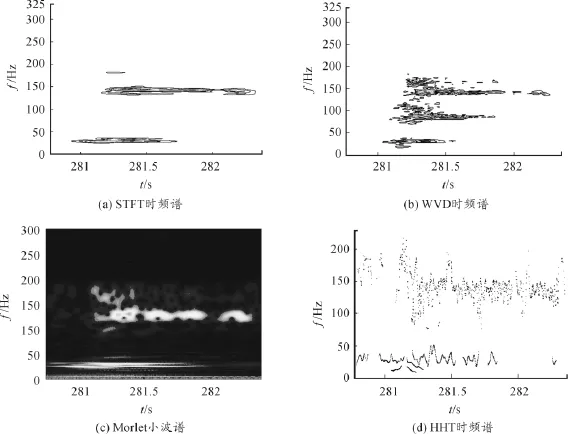
图5 实测信号的的STFT、WVD、Wavelet及HHT谱

利用直接延拓法对实测信号数据两端各延拓10个数据点，再进行EMD分解和HHT变换，然后抛弃延拓的数据点，进行EMD和HHT变换得到图5（d）的时频谱和图6的三维空间谱。

从图6时频谱图可以清楚的看到27 Hz和140 Hz左右频率分量随时间的变化情况，时频聚集性很好，且无交叉项干扰.如对27 Hz频率分量比较关注，可以提取该分量如图7，从图中可以清晰地看出27 Hz频率的变化情况。

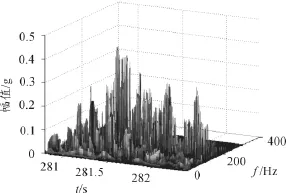
图6 HHT时间-频率-幅值谱

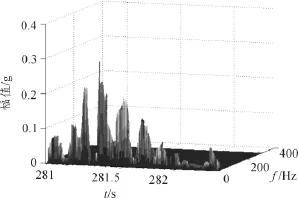
图7 27 Hz频率分量时频谱

3 结论

文章阐述了几种典型的时频分析方法：短时傅立叶变换、Wigner-Ville分布、小波变换以及HHT变换，并进行了理论分析研究和仿真验证，描述了各方法的优点和缺点。

利用典型的时频分析方法对实测火箭振动数据进行分析对比，表明HHT是一种良好的非平稳信号处理方法，它突破了以傅立叶变换全局性表示为基础的传统信号处理方法的不足，从信号本身出发不需要选择窗函数、基函数等先验条件，不再受Heisenberg测不准原理的约束，能同时在时频两域取得良好的集聚性，且无交叉项干扰，是火箭振动数据时频分析的有力途径。

［1］陈以恩，李连周，于谟，等.遥测数据处理［M］.北京:国防工业出版社，2002:45-56.

［2］张宁.自适应时频分析及其时频属性提取方法研究［D］.青岛:中国海洋大学地球探测与信息技术，2008:10 -11.

［3］卫俊平.时频分析技术及应用［D］.西安电子科技大学电子工程学院，2005:23-31.

［4］王红萍.非平稳信号时频分析方法性能研究［D］.南京:南京航空航天大学自动化学院，2008:42-51.

［5］李文，刘霞，段玉波.基于小波熵与相关性相结合的小波模极大值地震信号去噪［J］.地震学报，2012，34（6）:841 -850.

［6］董璐璐，房文静，徐静.基于小波模极大值的测井信号滤波［J］.测井技术，2012，36（2）:141-145.

［7］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for non linear nonstationary time series analysis［J］.Proc.R.Soc，London，1998，A 454:903-955.

［8］张义平，李夕兵.爆破振动信号的HHT分析与应用［M］.北京:冶金工业出版社，2009:33-52.

［9］QIAN Chang Song，LIU Dai Zhi，LIU Zhi Gang，et al.EMD based on recursive high-pass filter and its application on seismic signal analysis［J］.Chinese Journal of Geophysics，2010，53（5）:1215-1226.

［10］Wang Chenxing.Da Feipeng.Adaptive Phase Extraction Method Based on Hilbert-Huang Transform［J］.ACTA OPTICA SINICA.2012，32（11）:548-557.

［11］Zhang Jianhai，Han Yingchun，Li Lianzhou，et al.An improved EMD time-frequency analysis method for rocket vibration signal［C］//IEEE Chinese Guidance，Navigation and Control Conference，2014，1842-1846.

（责任编辑唐定国）

Time-Frequency Analysis Application on Rocket Vibration Data

ZHANG Jian-hai1，2，HAN Ying-chun1，2，ZENG Yan-yan2，WU Gong-you1，LI Lian-zhou2
（1.State Key Laboratory of Astronautic Dynamics，Xi'an 710043，China；2.Xi'an Satellite Control Centre，Xi'an 710043，China）

In order to accurately analyze rocket vibration data and offer powerful evidence for improving rocket design and performance analysis，several typical time-frequency method as well as their principles and features were researched and simulated.An algorithm model for time-frequency analysis on measured data was proposed according to the characteristics of rocket vibration data.The results show that the Hilbert-Huang transform，which is of good adaptive characteristics and optimal time-frequency resolution，is a good time-frequency method for rocket vibration data.

time-frequency analyses；HHT；non-stationary signal

张建海，韩迎春，曾艳艳，等.时频分析方法及其在火箭振动数据分析中的应用［J］.四川兵工学报，2015（11）：86-90.

format：ZHANG Jian-hai，HAN Ying-chun，ZENG Yan-yan，et al.Time-Frequency Analysis Application on Rocket Vibration Data［J］.Journal of Sichuan Ordnance，2015（11）：86-90.

V11

A

1006-0707（2015）11-0086-05

10.11809/scbgxb2015.11.023

2015-05-12

国家自然科学基金资助项目（11276072）；宇航动力学国家重点实验室基础研究资助项目（2013ADL0208）

张建海（1980—），硕士，工程师，主要从事火箭环境数据高精处理研究。