基于弹道预测与倾角校正的末制导炮弹导引方法

张华，常思江，牛春峰

（1.南京理工大学能源与动力工程学院，南京210094；2.中国兵器工业导航与控制技术研究所，北京100089）

基于弹道预测与倾角校正的末制导炮弹导引方法

张华1，常思江1，牛春峰2

（1.南京理工大学能源与动力工程学院，南京210094；2.中国兵器工业导航与控制技术研究所，北京100089）

为了提高炮弹的精确打击能力，以某制导炮弹为研究对象，对适配的快速弹道预测方法和末段导引方法进行了研究。通过对三自由度质点弹道方程进行解析求解，建立了一个精度良好、运算速度较快的弹道预测解析模型，提出了相应的剩余飞行时间计算模型；根据预测落点与目标点之间的位置偏差，提出了一种基于弹道倾角校正的末段导引方法，并进行了数值仿真。仿真结果表明，该导引方法在不同弹道条件下均具有较好的应用效果，可有效提高制导炮弹的精度。

制导炮弹；弹道预测；剩余飞行时间；末段导引方法

低间接伤害概率和高精度打击逐步成为现代战争对弹药武器的基本要求［1］。将常规炮弹进行改造使之成为具有制导控制能力的制导炮弹，无疑是最具效费比的方式之一，近年来已引起各国的广泛关注［2-3］。与一般的战术导弹相比，制导炮弹的无控飞行段较长，控制能力较弱，故发展制导炮弹的一个关键问题是要研究适配的导引方法。Park Woosung、曾庆华等人通过由离线仿真训练好的神经网络得出相关参数，并将其用于在线制导［4-5］。常思江、王中原等人对质点弹道方程进行数学解析得到弹道预测解析模型及剩余飞行时间来对弹丸落点进行预测，并设计了与不同性能要求相适配的末段导引方法［6-7］。周卫文、史鲲等人对反馈线性化的预测制导律进行了改进，基于预测控制方法的输出跟踪形式，提出了连续时间预测控制理论［8］。以上研究都针对所提出对象的特点和特殊性能要求，研究并分析了与之相适配的导引方法。本研究以制导炮弹为对象，充分考虑制导炮弹无控飞行特性，提出一个基于快速、准确弹道预测与弹丸飞行倾角修正的导引方法，以期为制导炮弹的工程研究提供参考。

1 弹道预测方法

考虑到需在弹载设备上实时预测落点，本研究选取三自由度弹道模型进行研究［9］；选取地面坐标系下弹丸的位置坐标（x，y，z）和速度分量（vx，vy，vz）进行研究计算。选取极小段时间Δt，假定Δt内，弹丸的速度大小不发生变化，即，则弹丸质心运动方程组为

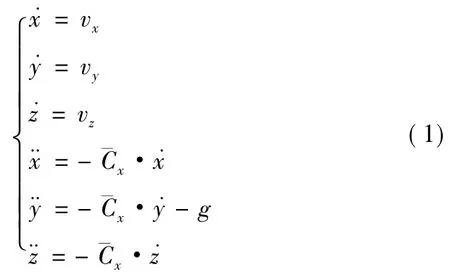
求解式（1）中的后3个特征方程的特征值，代入初始条件t=0，x=x0，y=y0，z=z0，并对时间进行一次求导，可得

式中：A=-Cx·t；（x0，y0，z0）为弹丸当前位置；（vx0，vy0，vz0）为当前速度分量，由测量系统传入实时数据；大气密度ρ根据气象标准条件得到；阻力系数Cx值可根据当前马赫数从预先编制的马赫数-阻力系数数值表中插值得到［10］。因此，可以得到当前弹丸飞行t时间后所处的位置（x，y，z）和速度分量（vx，vy，vz）。

对飞行弹丸进行受力分析，质心高度y方向上的动力学方程为

式中：ym为落点高度；v0为弹丸当前飞行的总速度；vy0为弹丸当前飞行速度在y轴方向上的分量；tgo为剩余飞行时间；ψ2为弹丸当前飞行的弹道偏角；θa为弹丸当前飞行的弹道倾角。

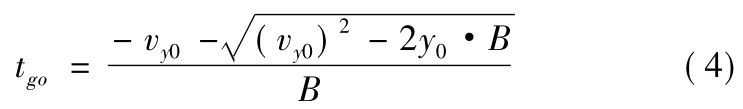
将tgo表达式代入方程组（2）可得

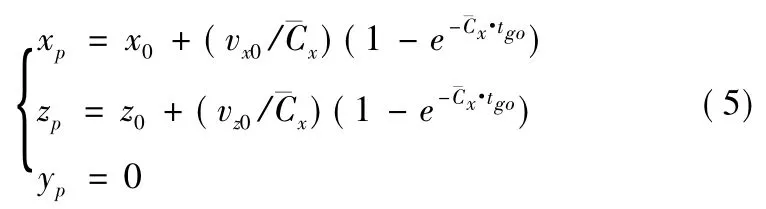
式中，（xp，yp，zp）即为弹道预测落点坐标。

式（2）～式（5）即为基于三自由度弹道方程组的弹道预测模型。选取初速v0=1 000 m/s，在不同射角下对该弹道预测模型进行数值仿真，仿真结果如表1所示。

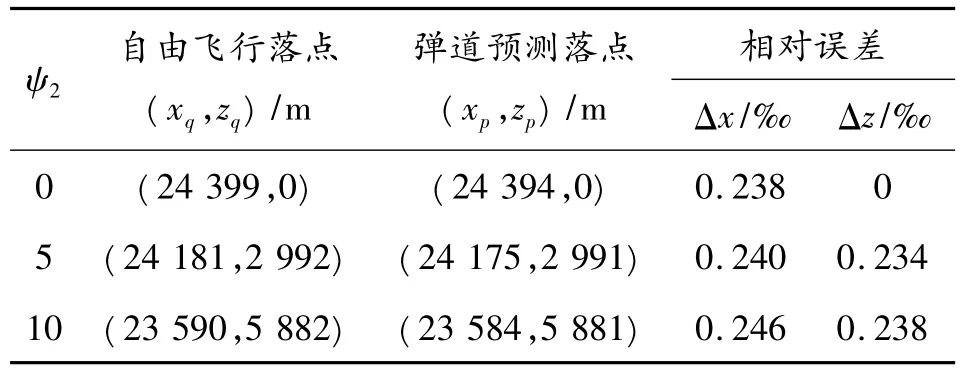
表1 弹道倾角θa=45°下弹道预测结果

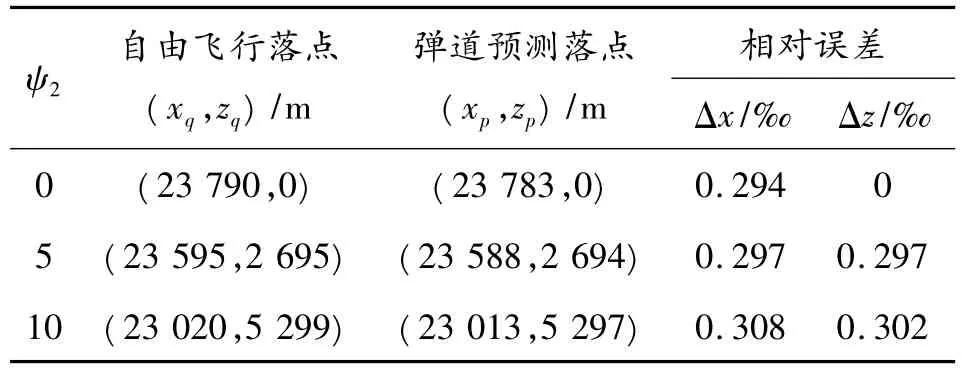
表2 弹道倾角θa=40°下弹道预测结果

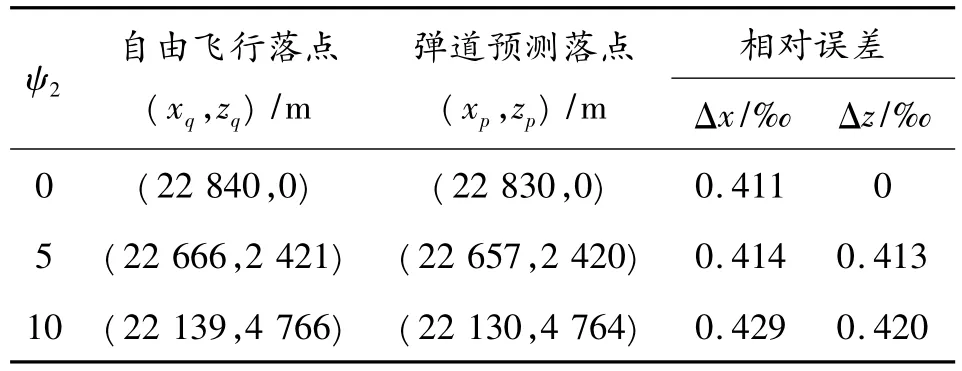
表3 弹道倾角θa=35°下弹道预测结果

表1～表3分别在弹道倾角θa=45°，40°，35°和弹道偏角ψ2=0°，5°，10°下进行仿真，在地面坐标系x轴方向和z轴方向上偏差的距离相对于弹丸自由飞行全程的相对误差随θa，ψ2有微小变化，但相对误差值都在0.5‰以内。仿真结果表明，该弹道预测方法具有良好的精度，可用于实际工程。

2 末段导引方法

2.1 基本原理

本节将讨论一种基于倾角校正的制导炮弹末段导引方法。假设弹丸在降弧段某高度处开始导引，由前述弹道预测模型计算出预测落点，并对目标位置进行对比，得到的位置偏差用于引导弹丸进行弹道修正，其原理如图1和2所示，其中图1是弹道在铅垂面上的投影，图2是弹道在水平面上的投影。

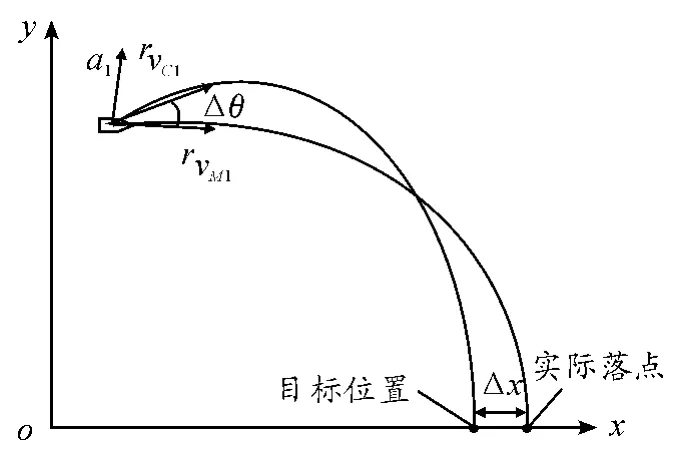
图1 铅垂面末段导引示意图

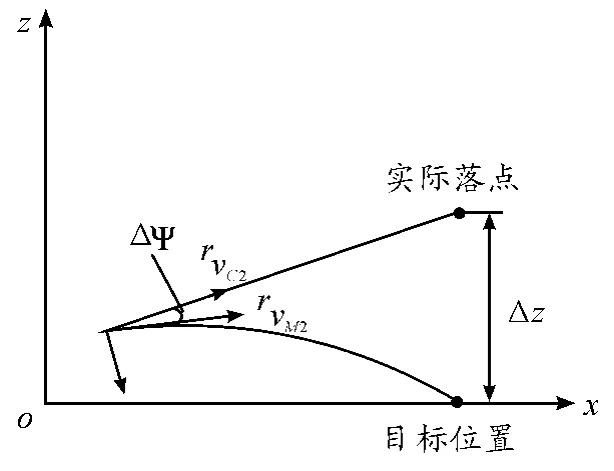
图2 水平面末段导引示意图

如图1所示，分析弹丸在铅垂面内的运动，在到达起始导引位置后进行末段导引。分别为当前弹道和理想弹道上的速度矢量在铅垂面上的分量，且。若弹丸自由飞行，在速度下弹丸不能达到目标位置；当弹丸在速度下时，弹丸则可沿弹道轨迹击中预定目标。弹丸速度无法从突变到，而需要在一个周期Δt内完成对弹丸姿态的校正。根据x方向和z方向上的位置偏差量Δx， Δz，在铅垂面上，到所需的法向加速度为

式中：k1为导引常数；Δθ为从的弹道倾角修正量，控制周期为Δt提前设定值。

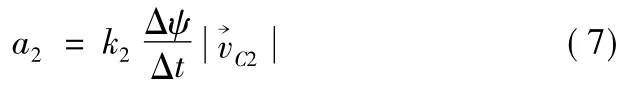
式中：k2为导引常数；Δψ为从到的弹道偏角修正量。

导引常数k1，k2通过仿真结果确定。Δθ，Δψ根据弹丸落点预测模型计算出的位置偏差量Δx，Δz通过如下公式得到

式中：弹丸落点误差Δx=xT-xp，Δz=zT-zP；（xT，zT）为目标位置坐标；为θ，ψ关于x，z的敏感矩阵，可由如下近似矩阵得到

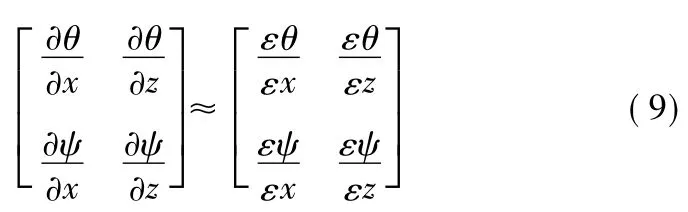
式中：ε为提前设定的极小量；εx=xp1-xp，εz=zp1-zp，其中（xp1，zp1）为受扰弹道落点位置，通过对弹丸当前弹道倾角θa和弹道偏角ψ2进行轻微扰动后得到的弹道倾角θa+εθa和弹道偏角ψ2+εψ2代入式（2）～式（5）计算得到。

2.2 导引流程

以某制导炮弹为例，在降弧段指定高度起始点进行末段制导，以预测落点与目标点间的位置误差为制导信号，经过该末段导引方法得到对弹丸进行控制的加速度指令，其导引流程如图3所示。

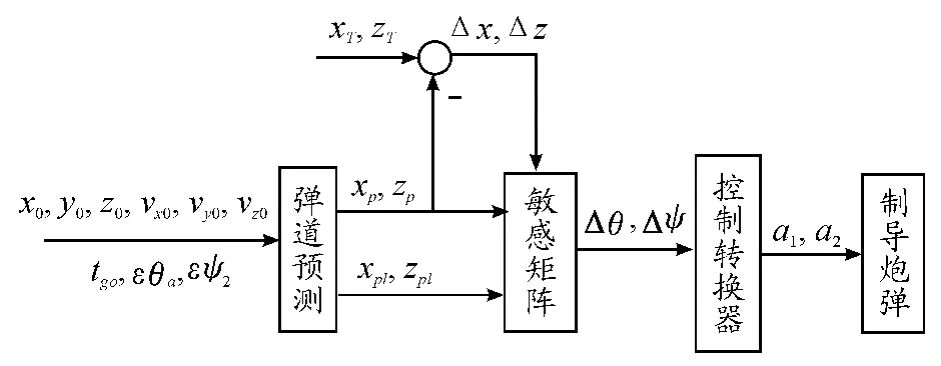
图3 导引流程

在图3中，将制导炮弹飞行过程中的实时参数（x0，y0，z0，vx0，vy0，vz0）及相应的剩余飞行时间tgo传入弹道预测模型得到一组预测落点（xp，zp），与目标点位置（xT，zT）计算预测误差Δx，Δz。同时将微小扰动量εθa，εψ2代入θa，ψ2中，计算出扰动后的一组预测落点（xp1，zp1），再与（xp，zp）计算出εx，εz，并与Δx，Δz一起代入式（8）和式（9），得到当前弹道倾角θa和弹道偏角ψ2所需要修正的偏差量Δθ，Δψ。将Δθ，Δψ代入控制转换器中，根据式（6）和式（7）得到该制导炮弹分别在铅垂面和水平面上的加速度指令a1，a2，并代入制导炮弹的执行机构完成具体的控制工作。

3 算例仿真

为验证上述导引方法的有效性，本节以某末制导炮弹为例进行仿真分析。仿真条件为炮口初速800 m/s，起始导引位置为降弧段2 000 m高度处，选取标准弹道条件θ0=45°，ψ0=0°；为了考察本文导引方法的精度，选取3组非标准弹道条件进行仿真①θ0=44.5°，ψ0=0.5°；②θ0=45°，ψ0= 0.5°；③θ0=45.5°，ψ0=0.5°。仿真结果如图4所示。

图4 加速度仿真结果

图4（a）～图4（c）分别表示该制导炮弹在不同初始条件下采用本研究提出的基于快速弹道预测的末段导引方法后得到的加速度指令a1，a2随时间的变化。由图4可知，弹丸起始导引时间为61.06 s，图4（a）、图4（b）、图4（c）中经过末段导引后弹丸落地的时间分别为72.22 s，72.16 s，72.12 s。因为弹丸在侧向的分速度比较小，因此修正弹丸偏航误差的制导加速度a2变化率较小。弹丸在铅垂面内的分速度随着高度的降低在不断增大，因此a1的变化律较大且随着时间的增加而增大。

目标靶的位置设为（19 000，0）m，给弹丸加一个初始弹道偏角ψ0=0.5°来表示弹丸飞行过程中所受到的干扰，故该制导炮弹在无控飞行时会对侧向产生位移，其无控飞行落点为（19 286.17，168.31），与目标点的位置偏差矢量为（286. 17，168.31）。而在该制导炮弹的末段弹道上，采用提出的末段导引方法对其进行导引，得到的实际落点与目标点的位置偏差如表4所示。

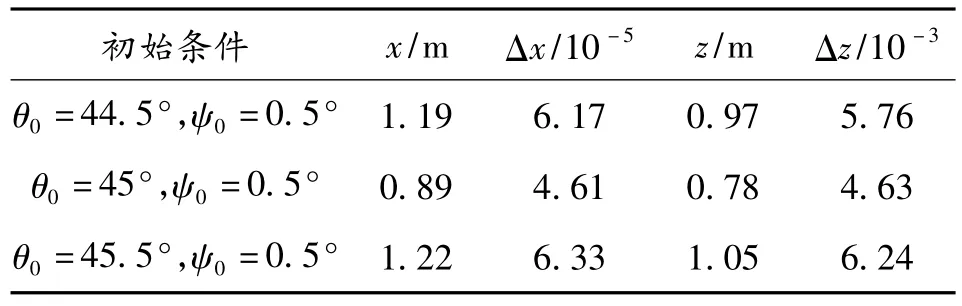
表4 不同条件下末段导引结果

从表4可以看出，弹丸落点与目标位置距离在5m范围内，比较好地实现了对该制导炮弹的末段弹道修正。

4 结束语

本研究以某制导炮弹为对象，通过对炮弹的三自由度质点弹道方程进行解析求解，研究了一种基于弹道预测与倾角校正的末制导炮弹导引方法，并对该方法进行了算例仿真。仿真结果表明，提出的基于弹道预测的末段导引方法可以有效地提高该制导炮弹的落点精度，研究结果对末制导炮弹的工程应用具有一定参考价值。

［1］WEY P.Performance analysis of ISL's guided supersonic projectile［C］//23rd International Symposium on Ballistics. Tarragona，Spain:IBC，2007:655-663.

［2］CHO H J，RYOO C K，TSOURDOS A，et al.Optimal Impact Angle Control Guidance Law Based on Linearization About Collision Triangle［J］.Journal of Guidance，Control，and Dynamics，2014，37（3）:958-964.

［3］侯瑞茵，李俨，侯明善.比例积分追踪制导方法研究［J］.西北工业大学学报，2014，32（2）:303-308.

［4］PARK W，RYOO C K，KIM B S，et al.A New Practical Guidance Law for a Guided Projectile［R］.Oregon，USA: AIAA，2011:2-9.

［5］曾庆华，董荣华，皮术武.基于最优制导模板的神经网络预测制导方法［J］.国防科技大学学报，2014，36（1）:137 -141.

［6］常思江，王中原，刘铁铮，等.鸭舵控制防空制导炮弹导引方法［J］.南京理工大学学报，2014，38（1）:123-128.

［7］常思江，曹小兵，刘铁铮.基于弹道预测的脉冲修正弹末段控制方法［J］.海军工程大学学报，2012，24（6）:84 -88.

［8］周卫文，史鲲，梁晓庚.基于预测控制的寻的导弹末制导律研究［J］.弹箭与制导学报，2013，33（4）:4-8.

［9］韩子鹏.弹箭外弹道学［M］.北京:北京理工大学出版社，2008.

［10］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2012.

（责任编辑周江川）

Guidance Law for Guided Projectiles Using Trajectory Prediction and Flight Path Angle Correction

ZHANG Hua1，CHANG Si-jiang1，NIU Chun-feng2
（1.School of Energy and Power Engineering，Nanjing University of Science&Technology，Nanjing 210094，China；2.Navigation and Control Technology Institute，China North Industries Group Corporation，Beijing 100089，China）

To improve the hit precision of guided projectiles，the suitable application process of rapid trajectory prediction law and terminal guidance law were discussed.Through the analytical solution of the 3D point mass trajectory equations，an analytical model with good accuracy and the corresponding algorithm for less time-consuming time-to-go estimation was also proposed.According to the position errors between the predicted impact point and the target，a terminal guidance law was proposed based on the correction rate of flight path angle，and then the numerical simulation was conducted.The simulation results indicate that under different trajectory conditions，the guidance law is satisfactorily effective and less timeconsuming to improve the hit precision.

guided projectiles；trajectory prediction；time-to-go；terminal guidance law

张华，常思江，牛春峰.基于弹道预测与倾角校正的末制导炮弹导引方法［J］.四川兵工学报，2015（11）：57-60.

format：ZHANG Hua，CHANG Si-jiang，NIU Chun-feng.Guidance Law for Guided Projectiles Using Trajectory Prediction and Flight Path Angle Correction［J］.Journal of Sichuan Ordnance，2015（11）：57-60.

TJ765.1

A

1006-0707（2015）11-0057-04

10.11809/scbgxb2015.11.016

2015-06-19

张华（1992—），男，硕士研究生，主要从事弹箭飞行与控制研究；通讯作者：常思江（1983—），男，博士，硕士生导师，主要从事弹箭飞行动力学与制导控制技术研究。