马尔科夫理论在引信安全系统可靠性分析中的应用

许皓文，尚雅玲，惠江海

（海军航空工程学院兵器科学与技术系，山东烟台264001）

马尔科夫理论在引信安全系统可靠性分析中的应用

许皓文，尚雅玲，惠江海

（海军航空工程学院兵器科学与技术系，山东烟台264001）

提出了一种运用马尔科夫理论进行安全系统可靠性分析的方法，对安全系统的模型进行了改良，对比了各种结构的安全性与可靠性差异；证明了在引信安全系统逻辑结构中，可恢复与冗余的设计的优越性，对引信安全系统设计有一定的参考价值。

引信安全系统；可靠性分析；马尔科夫理论

安全性与可靠性是引信安全系统设计的关键性指标，针对安全性与可靠性研究的方法也不尽相同。施坤林等人首先提出了应用马尔科夫理论对引信的安全性进行分析。张贤彪、何光林等人利用马尔科夫理论对各种逻辑结构进行了研究分析，提出了多环境、顺序、冗余、时间窗、可恢复等提高引信安全性的办法。可是利用马尔科夫理论并未对引信安全系统作用可靠性进行验证。

安全性即引信防止在感受到预定的发射环境并完成延期解除保险之前解除保险的能力。作用可靠性即引信防止在感受到预定的发射环境之后即刻解除保险的能力。提高系统的复杂程度，可以使引信的安全性得到提升，然而一味提高，就会伴随系统作用可靠性的降低。

所以，本文利用马尔科夫理论，对各种逻辑结构的安全系统的作用可靠性进行分析，并与安全性进行比较，综合安全性与作用可靠性对各结构对系统的影响能进行评估。

1 作用可靠性计算方法

对环境信息的错误判断为pn，它出现具有独立增量性、齐次性、普通性，所以假设错误出现的次数服从泊松分布，为

根据文献［1］，pn可视为常数。

如果环境信息出现且符合条件，则引信安全系统一定解除保险。作用可靠性概率即为当环境因素满足解除保险条件，但引信安全系统未解除保险的概率。

2 引信安全系统各结构作用可靠性分析

为对比各种结构的性能，设解除保险的错误概率pn为10-3。因为对比基本系统，为了使数据对比更明显，取n=10时，各结构的作用可靠性概率做比较。多环境保险结构如图1所示。

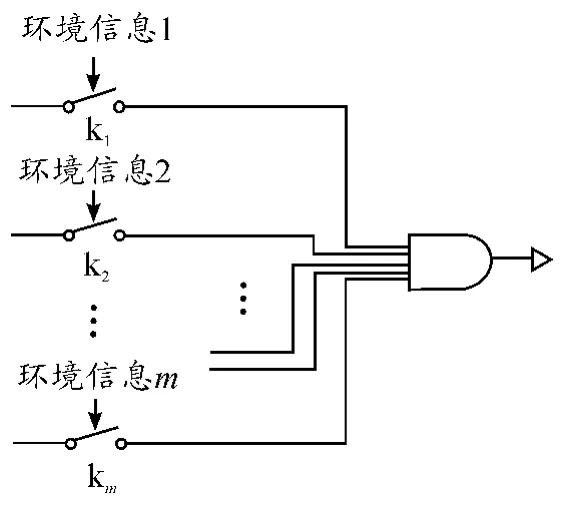
图1 m环境保险结构

有m个环境控制m个顺序保险结构，I=（i1，i2，…，im），i1为保险状态；i2～im-1为半保险状态；im为解除保险状态。

列出转移概率矩阵∏，根据n步转移概率矩阵∏n可以得到在n时段解除保险的概率。计算得单一环境作用可靠性概率

双环境作用可靠性概率

三环境作用可靠性概率

依据类推法

增加环境信息数量，作用可靠性指数级不变，指数级为10-3n，m环境独立不可恢复结构得到意外不接触保险的概率则为m×10-3n。随着环境的增加，作用可靠性的减少不明显。

双环境独立可恢复结构如图2所示。I=（i1，i2，i3，i4），i1为保险状态；i2为半保险状态（k1解除保险，k2为保险状态）；i3为半保险状态（k1为保险状态，k2为解除保险状态）；i4为解除保险状态。

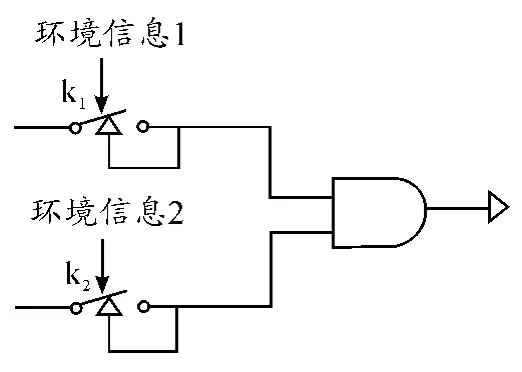
图2 双环境独立可恢复结构

文献［1］中的状态转移矩阵，当系统解除保险概率为1并且环境同时出现时，理想情况下，不能保证解除保险概率为1，所以采用如下状态转移概率矩阵

只有当在n时段，同时满足条件时，系统才解除保险，否则进入i1保险状态。当n时段的时间取得足够小，即可模拟系统连续状态。

根据n步转移概率矩阵∏n可以得到在n时段解除保险的概率：

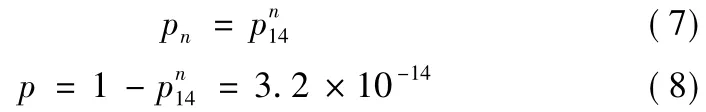
双环境顺序控制结构如图3所示。I=（i1，i2，i3，i4），i1为保险状态；i2为半保险状态（k1解除保险，k2为保险状态）；i3为保险状态（k1为保险状态，k2为保险状态）；i4为解除保险状态。

图3 双环境顺序控制结构

转移概率矩阵为

引入i3保险状态，当环境信息2出现而环境信息1未出现时，认为没有顺序进行解除保险过程，所以进入i3状态后，会返回i1状态，继续判定是否满足解保条件。

根据n步转移概率矩阵∏n可以得到在n时段解除保险的概率：

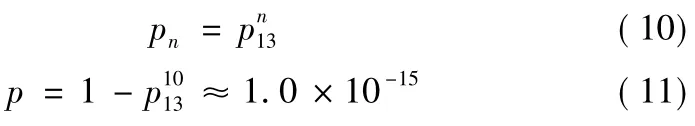
双环境顺序加时间窗如图4所示。I=（i1，i2，i3，i4，i5），i1为保险状态；i2为半保险状态（k1解除保险，k2为保险状态）；i3为保险状态（k1为保险状态，k2为保险状态）；i4为解除保险状态；i5为瞎火状态。

图4 双环境顺序加时间窗

转移概率矩阵为

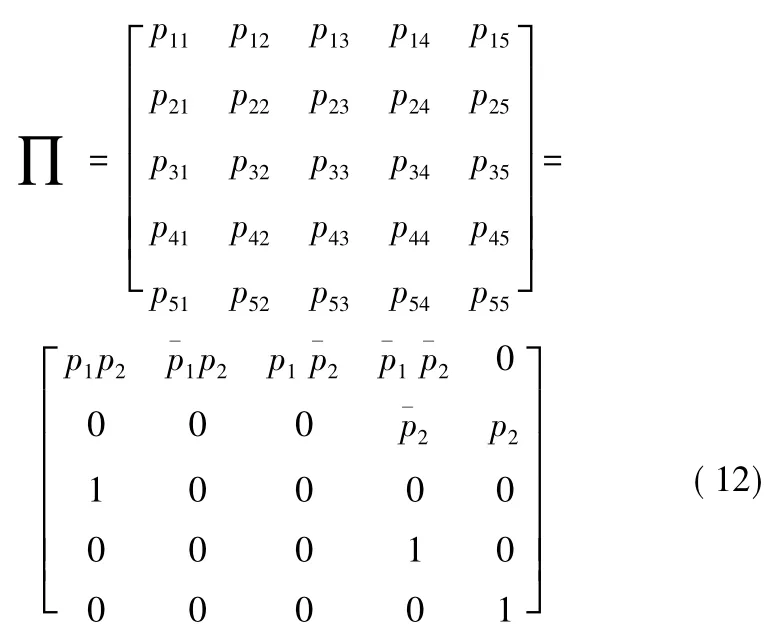
当没有按照顺序出现时，进入状态i3，而i3可以返回状态1，继续判断环境信息是否正确。当进入状态i2时，即k1已经解除保险但k2未解除保险时，则下一阶段判断环境信息2是否出现，如果出现，则解除保险；没有出现，则不符合时间窗，系统进入瞎火状态。

根据n步转移概率矩阵∏n可以得到在n时段解除保险的概率：

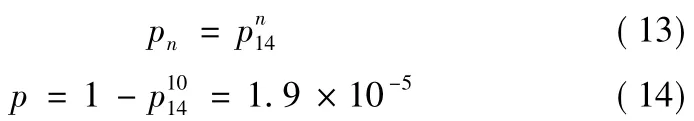
双环境非顺序则瞎火如图5所示。I=（i1，i2，i3，i4，i5），i1为保险状态；i2为半保险状态（k1解除保险，k2为保险状态）；i3为解除保险状态；i4为瞎火状态（k4打开）。

图5 双环境非顺序则瞎火

转移概率矩阵为

当环境信息2出现，而环境信息1未出现时，认为非顺序，则进入i4即瞎火状态。根据n步转移概率矩阵∏n可以得到在n时段解除保险的概率：

双环境冗余保险如图6所示。

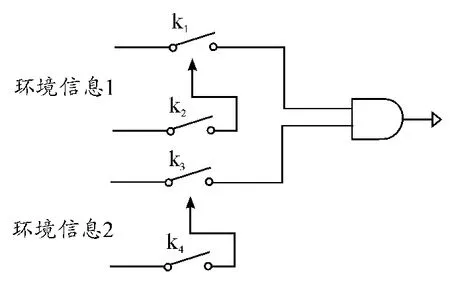
图6 双环境冗余保险

环境信息1与环境信息2输送给两个判断机构，其中一个将结果送给另一机构共同判断。其中k1与k2，k3与k4的判定机制相同。设使k1、k2动作的激励出现概率为p1，使k3、k4动作的激励出现概率为p2。在k2、k4信息传输过程中，出现传输错误的概率为p3。

转移概率矩阵为

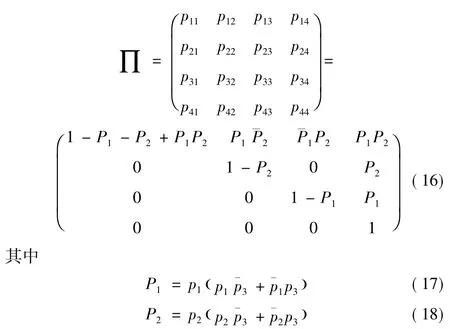
其中p3为冗余代价，即冗余操作出现错误判断的概率，这里设p3=10-3。

根据n步转移概率矩阵∏n可以得到在n时段解除保险的概率

则引信作用可靠性概率为

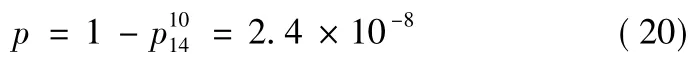
3 各级系统安全性与作用可靠性对比

对安全性进行计算，根据文献［1］，取p1=p2=10-3。取p1=p2=10-3，n=10时，对作用可靠性进行计算。得到各系统安全性与作用可靠性对比如表1所示。

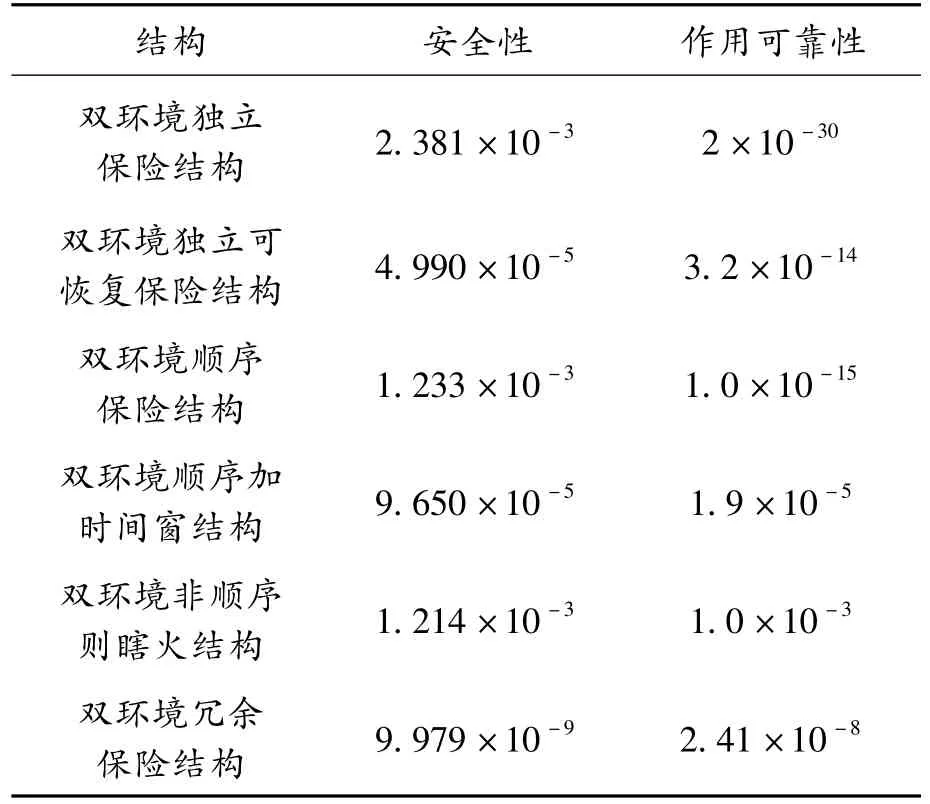
表1 各结构安全性与作用可靠性对比

上述安全性与作用可靠性参数越小，则安全性与作用可靠性越高。

双环境独立保险结构设计简单，所以作用可靠性很高，但它的安全性极差，安全系统设计中，其可靠性为首要考虑因素，所以独立保险结构不适用于安全系统。独立可恢复保险结构与顺序保险结构相比，前者的安全性提高明显，而二者的作用可靠性差距不大，所以认为可恢复结构相对优于顺序结构。时间窗结构对安全性的提高也十分显著，但是采用顺序加时间窗结构的安全性与只采用可恢复结构的安全性相当，但作用可靠性下降明显。加入瞎火设计，引信的安全性基本不变，但作用可靠性却大幅下降。冗余保险结构，在保证安全性的前提下，作用可靠性也很高，具有优良的性能。

根据结果，发现对提高系统的作用可靠性来讲，冗余结构优于可恢复结构，优于时间窗，优于顺序结构。

4 结论

本文设计了一种使用马尔科夫理论衡量系统作用可靠性的方法，并利用此方法计算了引信安全系统常采用的时间窗，顺序，瞎火结构的安全性与作用可靠性概率，计算过程中有一定的近似化处理，所以单独应用不能定量说明系统的可靠性程度，但可以通过对比分析安全系统逻辑结构在可靠性方面的优劣。通过对比分析，发现采用可恢复及冗余措施，能较好的保证安全性与作用可靠性。证明了可恢复与冗余设计在引信安全系统中的优越性。此方法对引信安全系统可靠性评估具有一定的参考价值。

［1］施坤林，谭惠民.马尔可夫理论在引信安全系统安全性分析中的应用［J］.现代引信，1991（4）:9-20.

［2］张贤彪，尚雅玲.引信安全系统信息控制逻辑分析［J］.四川兵工学报，2010（1）:32-35.

［3］何光林.引信安全系统解除保险逻辑分析［J］.北京理工大学学报，2008（12）:1084-1087.

［4］安晓红，赵河明，张亚.“引信安全系统失效率计算方法”的修订原则探讨［J］.华北工学院学报，2005（2）:92 -95.

［5］段志薇，谢光青.GO法在引信可靠性分析中的应用［J］.机械工程与自动化，2010（1）:131-132.

［6］陈军文.从美军引信设计可靠性工作谈我军弹药可靠性研究［J］.四川兵工学报，2000，21（4）:16-18.

［7］刘卫东，胡勇克，吴文伶，等.典型引信机构安全性与可靠性的估计［J］.南昌大学学报，2000，22（4）:14-17.

［8］周平，牟洪刚，刘勇，等.机电引信串联和并联模型可靠性评估方法.探测与控制学报［J］.2009（6）:51-54.

［9］李东兵，王力强，潘鸿飞.武器装备系统可靠性工程综述［J］.战术导弹技术，2003（6）:12-20.

［10］李宁，任翼翔，夏三保.机电引信可靠性增长试验方法［J］.兵工自动化，2009（8）:40-42.

［11］马宝华.现代引信的控制功能及特征［J］.探测与控制学报，2008（1）:1-5.

（责任编辑周江川）

Markov Theory in Reliability Analysis of Fuze Safety System

XU Hao-wen，SHANG Ya-ling，HUI Jiang-hai
（Department of Ordnance Science and Technology，Naval Aeronautical Engineering Institute，Yantai 264001，China）

A method that used Markov theory for reliability analysis of fuse safety systems was proposed and the model of safety systems was modified.The differences of reliability and safety of each structure were compared.This paper proved the superiority of re-safeing and redundant design in fuse safety system logical structure，which may provide some reference to the fuse safety system design.

fuse safety system；effectiveness analysis；Markov theory

许皓文，尚雅玲，惠江海.马尔科夫理论在引信安全系统可靠性分析中的应用［J］.四川兵工学报，2015（11）：41-44.

format：XU Hao-wen，SHANG Ya-ling，HUI Jiang-hai.Markov Theory in Reliability Analysis of Fuze Safety System［J］.Journal of Sichuan Ordnance，2015（11）：41-44.

TJ430.1

A

1006-0707（2015）11-0041-04

10.11809/scbgxb2015.11.012

2015-09-20

许皓文（1990—），男，硕士研究生，主要从事安全检测与起爆控制技术研究。