错缝拼装及土层刚度对盾构隧道横向刚度有效率的影响研究

王 谭，莫海鸿，陈俊生，杨春山

(1.华南理工大学土木与交通学院，广州 510641；2.亚热带建筑科学国家重点实验室，广州 510641)

错缝拼装及土层刚度对盾构隧道横向刚度有效率的影响研究

王 谭1，2，莫海鸿1，2，陈俊生1，2，杨春山1，2

(1.华南理工大学土木与交通学院，广州 510641；2.亚热带建筑科学国家重点实验室，广州 510641)

针对盾构隧道横向刚度有效率取值及其影响因素，借助有限元软件建立三维壳-弹簧模型，计算综合考虑错缝拼装与地层抗力作用下的横向刚度有效率，探讨不同错缝拼装角度和地层抗力系数对隧道横向刚度有效率的影响。结果表明：典型珠三角地区错缝拼装时的横向刚度有效率为0.75，较通缝拼装0.65增加了15%。横向刚度有效率随着错缝角度的增大而增大，当错缝角度超过45°时，刚度有效率的变化趋于稳定。横向刚度有效率随着地基反力系数的增大，呈现线性增长趋势。

盾构隧道；刚度有效率；修正惯用法；数值模拟；壳-弹簧模型

1 概述

修正惯用法因其概念明确、计算简便等优点在国内盾构隧道的设计与研究中得到广泛应用，该方法通过刚度有效率表示接头的存在对管片横向刚度的减弱效应，刚度有效率取值合理与否对于隧道衬砌设计计算至关重要。

黄宏伟等[1]通过相似模型试验得到通错缝隧道横向刚度有效率，并指出通错缝拼装刚度有效率的差异，但模型试验中仅满足部分物理量相似，与实际情况存在偏差，研究单纯从结构角度出发，未考虑土层抗力作用。

Lee K M[2]给出了盾构隧道通缝拼装情况下隧道横向抗弯刚度的有效率η，且得到了η和ξ各参数拟合关系式。彭益成[3-4]等在通缝拼装情况下分析了接头数量、接头角度、接头抗弯刚度和地基抗力系数对于弯曲刚度有效率的影响。上述研究均未考虑错缝拼装对横向刚度的增强效应，同时两者采用梁-弹簧模型难以反映管片空间力学特征对刚度有效率的影响。

基于此，本文在已有研究成果基础上，借助有限元法建立三维壳-弹簧模型，计算得到综合考虑错缝与地层抗力作用下的横向刚度有效率，分析了错缝拼装不同的错缝角度和地层抗力系数对隧道横向刚度有效率的影响，得到一些有益的结论，以期为盾构隧道横向设计计算提供参考。

2 计算模型建立

2.1 工程概况

某典型工程为广州市的生命线工程，该项目在穿越城区的大型交通枢纽位置时，采用了盾构隧道的非开挖施工方式，盾构段总长约2.357 km，最大埋深约20 m。隧道管片的结构尺寸为：外部直径为6 m，内径为5.4 mm，厚度300 mm，环宽1.5 m。管片按照传统的“3+2+1”的拼装模式所拼装，即3块标准块管片(A1～A3)，2块邻接块(BC)，1块封顶块(也称为楔形块)，衬砌结构的断面图及受荷示意如图1、图2所示。

对于隧道结构而言，无论其是埋置在土层环境还是岩层当中，其力学行为均是衬砌与周围地层相互作用的结果，不能割裂两者之间的联系。三维壳-弹簧模型能使盾构隧道空间综合力学特征得到较好的体现[5]，因此采用壳-弹簧模型对管片进行分析。

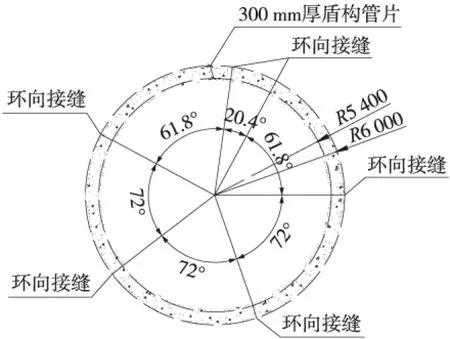
图1 衬砌结构断面

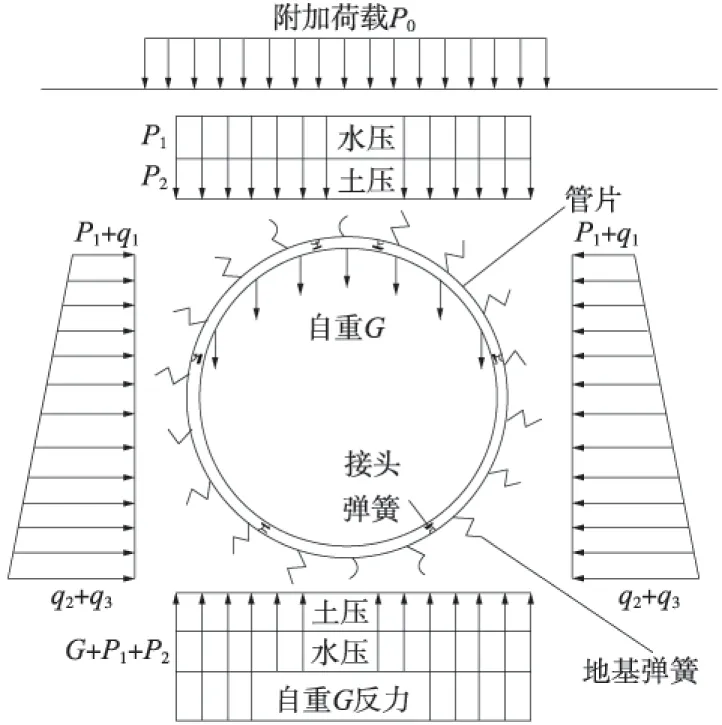
图2 衬砌结构-土层作用模型

。

2.2 土层参数与弹簧参数确定

根据该项目地质勘查报告与隧道结构设计方案可知，隧道所在及以上土层物理力学参数见表1。管片结构参数如下：外径(D)为6 m；螺栓直径为30 mm；混凝土弹性模量为3.45×107kPa；螺栓预应力为7.0×104kPa；内径(d)为5.4 m；螺栓长度为490 mm；螺栓弹性模量为2.06×108kPa；环宽为1.5 m。

表1 土层物理力学参数

2.3 管片外部水土压力计算

[6]公式计算单宽径向地基反力系数为

(1)

式中，kr为径向反力系数；E为弹性模量；v为土层泊松比。

根据表1参数可计算kr=14.1 MPa/m。

如图3所示，计算管片顶与底部水压分别为P1=185 kPa、q2=245 kPa。采用Terzaghi理论计算松动土压力[7]，计算图3中的各土压力。

洞顶松动半宽为

(2)

松动高度为

(3)

式中，R0为管片外径，m；φ为土体的内摩擦角，(°)；k0为侧压力系数，k0=1-sinφ′=0.507；γ为土层重度，kN/m3；H为上覆土厚度，m；P0为地面有超载，kPa，取20 kPa。

将表1中相关参数代入式(2)、式(3)计算可得B1=5.19 m，h0=13.49 m，p2=h0γ+p0=283.01 kPa；进而有：q1=k0p2=143.48 kPa；q3=k0p2+γR0=202.8 kPa。

拱底自重反力主要由下半环管片承受，自重反力G=2πR0lΔg/πR0l=2Δ·g=2×0.3×25=15 kPa。其中g为管片的重度，kN/m3；l为一个管片环宽度；Δ为管片厚度。根据计算，得到如图3所示衬砌结构受力。

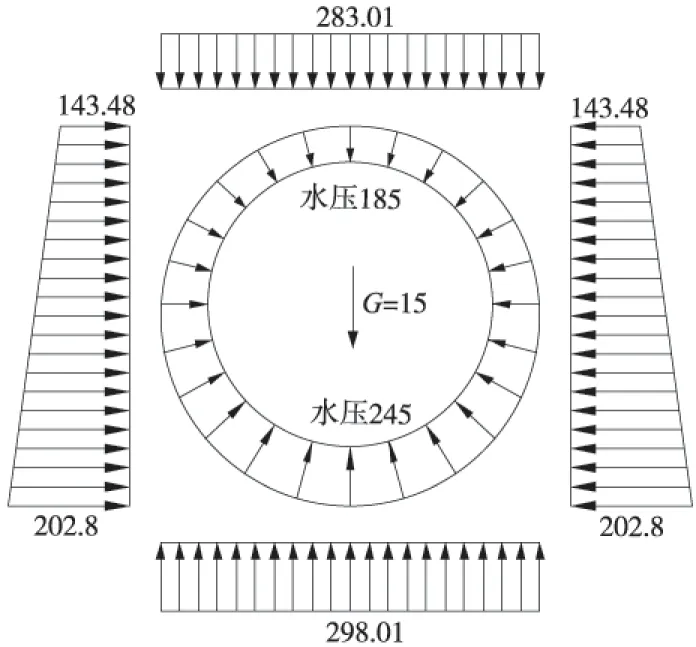
图3 衬砌结构受力(单位：kPa)

2.4 计算模型的确定

实际土层对隧道衬砌结构的作用等效为衬砌全周Winker地基弹簧。H Duddeck认为隧道埋深为大于6倍隧道半径，应考虑土拱效应[8]，土层弹簧既考虑受拉也考虑受压；朱合华等[9]计算一埋深16.8 m的隧道，对比分析认为采用全周拉压地层弹簧比较准确。

本文地层弹簧采用全周边界抗拉压模型，管片采用壳单元模拟、管片接头螺栓采用旋转弹簧、剪切弹簧及拉压弹簧单元模拟。采用虚拟全周边界与土弹簧连接，以模拟边界约束。

外部荷载作用下地基弹簧发生径向变形，地基弹簧长度要满足大于土层变形，此处取地基弹簧长度为0.5 m。

本模型中隧道管片的有限元模型如图4所示。

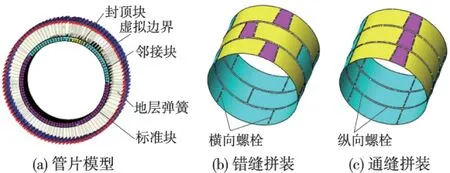
图4 有限元管片模型

3 数值计算结果分析

3.1 计算结果分析

图5为管片整体计算模型与中间环的位移云图。横向刚度有效率计算采用更接近实际情况的中间环的管片位移；由图5可见，错缝拼装管片的最大水平位移为6.1 mm，通缝拼装情况下的最大水平位移为7.1 mm，匀质圆环的最大水平位移为4.6 mm；经计算各种拼装情况下所达到的横向刚度有效率见表3。

图5 管片位移云图

拼装形式最大水平位移/mm最大竖向位移/mm横向刚度有效率匀质拼装4.65.21.13通缝拼装7.1—0.65错缝拼装6.1—0.75

刚度有效率计算结果表明，错缝拼装的刚度有效率较通缝拼装约增大15%，管片纵向错缝拼装对横向刚度起到了增强效应。匀质管片的最大竖直位移约为最大水平位移的1.13倍，符合实际情况下管片的变形情况。

3.2 模型的合理性验证

为了验证计算模型的合理性，进行理论计算结果与数值结果对比分析。取管片的1/4结构作为研究对象，具体受力示意见图6。管片受力模型见图7。

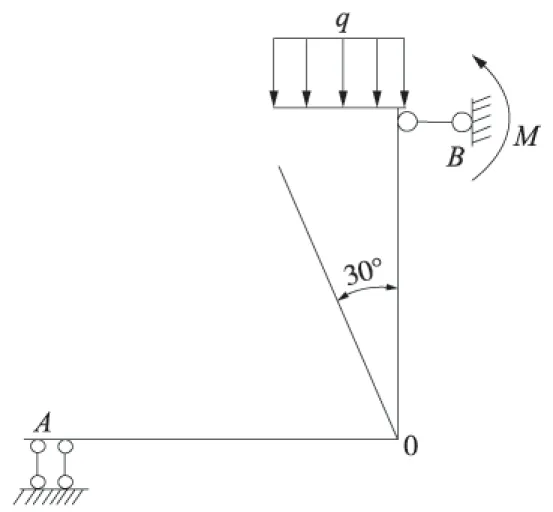
图6 1/4管片结构受力示意

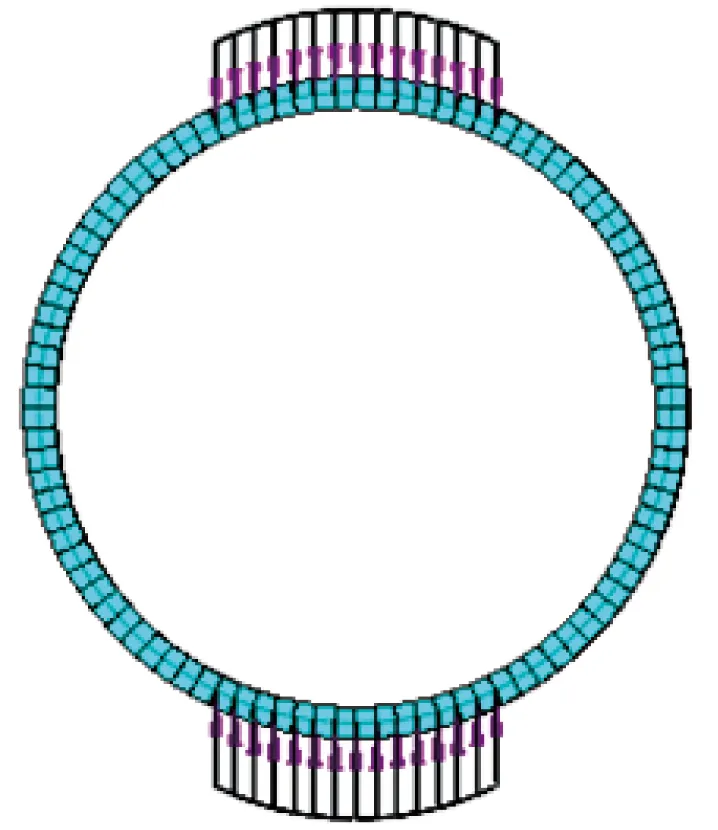
图7 管片模型受力示意

由结构力学知识求解隧道管片的竖向直径和水平直径处的变形值，具体如下。

水平直径处

(4)

竖向直径处

(5)

理论计算结果得到本例管片竖直向位移是水平位移的1.20倍，与数值计算结果1.13倍吻合，说明本文计算模型具备合理性。

4 刚度有效率对错缝拼装参数敏感性分析

衬砌结构的横向刚度有效率除了和衬砌环的结构尺寸、接头状况有关外，还与接头位置角度和周围的地层情况有关[10-12]。

4.1 管片刚度有效率对错缝角度的敏感性分析

接头位置角度表示从管片环顶部沿顺时针方向的第一个接头与管片环顶部所成的角度。为得到错缝角度的变化对管片横向刚度有效率的影响规律，现在原有模型的基础上改变错缝拼装模型的错位角度，分别为11.5°、22.5°、30°、45°。

图8 错缝角度与管片水平位移值的关系曲线

图8显示，盾构隧道错缝角度越大，隧道管片的水平位移值减小，则横向刚度有效率增大，当错缝角度达到45°时，隧道管片的水平位移值趋于不变，相应的横向刚度有效率也趋于接近。因此，盾构隧道管片的错缝角度对横向刚度有效率产生了一定影响，在进行隧道横向设计时应给予考虑。

4.2 管片刚度有效率对地基反力系数的敏感性分析

为了考察错缝拼装管片在荷载作用下产生的变形受地层抗力系数影响规律，在原有错缝拼装隧道模型的基础上改变地层弹簧的地基反力系数，得到地基反力系数和管片横向刚度有效率的关系曲线如图9所示。并进行一元线性拟合见表4。

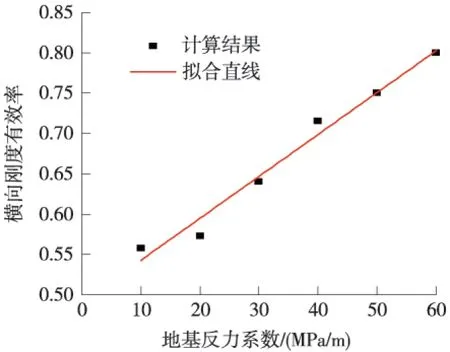
图9 错缝角度与水平位移值关系曲线

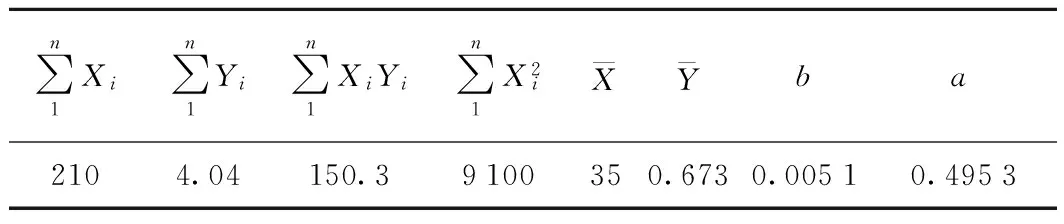
∑n1Xi∑n1Yi∑n1XiYi∑n1X2iXYba2104.04150.39100350.6730.00510.4953

表中

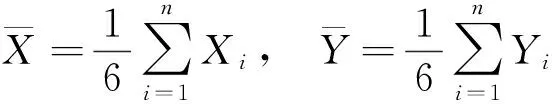
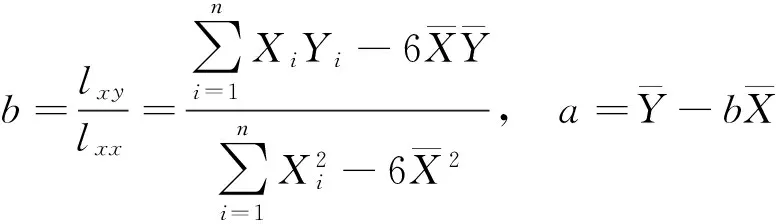
进行一元线性拟合的直线方程为

(6)

相关系数

(7)

图9显示，随着地基反力系数的增大，管片的横向刚度有效率近似线性增长，进行一元线性拟合，得到拟合直线的相关系数为0.992 7。因此地层抗力对管片刚度有效率产生了显著的影响，应给予充分考虑。

“这个是‘宝川’的小平钱，这个是‘宝苏’的小平钱……这个是‘宝济’，一元。‘宝广’，两元……一元……两元……”孟导开始自虐地对照起价格，越是对照越是失望。

5 结论

(1)错缝拼装情况下的横向刚度有效率比通缝拼装情况下增长了约15%。并通过与理论计算结果对比表明，模型具备合理性。

(2)隧道结构的横向刚度有效率随着错缝拼装角度的不同而变化；刚度有效率随着错缝角度的增大呈现增大的趋势，但当错缝角度超过45°时，横向刚度有效率的变化趋于稳定。

(3)隧道结构的横向刚度有效率受地基反力系数的影响，当地基反力系数增加10 MPa/m，横向刚度有效率增加约7%，两者近似呈现同向线性关系。

参考文献：

[1] 黄宏伟，徐凌，严佳梁，等.盾构隧道横向刚度有效率研究[J].岩土工程学报，2006，28(1)：11-18.

[2]LEE K M， GE X W. The equivalence of a jointed shield driven tunnel lining to a continuous ring structure[J]. Journal of Canadian Geotechnical Engineering， 2001，38:461-483.

[3]焦齐柱.盾构隧道管片计算模型参数的敏感性分析[J].铁道标准设计，2010(6)：93-95.

[4]彭益成，丁文其，闫治国，等.修正惯用法中弯曲刚度有效率的影响因素分析及计算方法[J].岩土工程学报，2013，35(1)：495-500.

[5]姚超凡，晏启祥，何川，等.盾构隧道内力分析方法的对比研究[J].铁道标准设计，2013(12)：95-99.

[6]A.M.Muir Wood. The circular tunnel in Elastic Ground[J]. Geotechnique， 1975，25(1)：115-127.

[7]陈俊生，莫海鸿.盾构隧道管片施工阶段力学行为的三维有限元分析[J].岩石力学与工程学报，2006，25(2)：3482-3489.

[8]DUDDECK H， Heinz， Erdmann. On structural design models for tunnels in soft soil[J]. Underground Space， 1985，9(56)：246-259.

[9]朱合华，崔茂玉，杨金松.盾构衬砌管片的设计模型与荷载分布的研究[J].岩土工程学报，2000，22(2)：190-194.

[10]裴利华.盾构隧道管片结构设计研究[J].铁道标准设计，2009(12)：86-91.

[11]陈俊生，莫海鸿.盾构隧道管片接头抗弯刚度的三维数值计算[J].铁道学报，2009，31(4)：87-91.

[12]张恒，陈寿根，陈亮.软硬不均地层盾构隧道管片力学行为研究[J].铁道标准设计，2012(8)：83-86，95.

The Impact of Staggered Joint and Soil Stiffness on Transverse Effective Rigidity Ratio of Shield Tunnel

WANG Tan1，2， MO Hai-hong1，2， CHEN Jun-sheng1，2， YANG Chun-shan1，2

(1.School of Civil Engineering and Transportation， South China University of Technology. Guangzhou 510641， China;2.State Key Laboratory of Subtropical Building Science， South China University of Technology， Guangzhou 510641， China)

In view of shield tunnel transverse effective stiffness value and its influencing factors， the finite element software is employed to establish a three-dimensional shell-spring model to calculate and analyze the transverse effective rigidity ratio in comprehensive consideration of staggered joint angle and strata resistance and to address the impact of staggered joint and soil stiffness on transverse effective rigidity ratio of shield tunnel. The results show that the transverse effective stiffness value in the typical pearl river delta region is 0.75， which is 15% increase compared with 0.65 for through joint assembling. The Transverse effective stiffness increases with the increase of the angle of staggered joint. When the staggered joint angle exceeds 45°， the change of the effective rigidity tends to be stable. The transverse effective stiffness tends to show linear growth with the increase of the coefficient of subgrade reaction force.

Shield tunnel; Effective bending rigidity; Modified routine method; Numerical simulation; Shell-spring model

2014-12-25；

2015-01-04

亚热带建筑科学国家重点实验室自主研究课题(2015ZC20，2012ZC27)

王 谭(1990—)，女，硕士研究生，2013年毕业于河南科技大学土木工程专业，工学学士，E-mail：wthnlgdx361@163.com。

陈俊生(1979—)，男，讲师，博士，E-mail：jschen@scut.edu.cn。

1004-2954(2015)09-0136-05

U455.43

A

10.13238/j.issn.1004-2954.2015.09.030