车辆荷载对基坑支护结构的影响分析

唐丽云,邱培勇,叶万军,杨更社

(西安科技大学建筑与土木工程学院,西安 710054)

车辆荷载对基坑支护结构的影响分析

唐丽云,邱培勇,叶万军,杨更社

(西安科技大学建筑与土木工程学院,西安 710054)

为了研究车辆荷载对基坑支护结构体系的影响,针对常规等效代换土层厚度法未考虑破裂棱体破裂角变化问题,引入改进等效代换土层厚度法,依据库伦土压力理论,计算破裂棱体自重,结合破裂棱体平衡关系式,循环迭代得到破裂角收敛值,根据此破裂角换算得到新的土层厚度。基于地铁车站基坑工程,通过数值模拟,采用常规方法和改进的等效代换土层厚度法研究车辆荷载对基坑支护结构的影响,分别得到支护结构的水平位移曲线。研究表明,破裂角变化会引起代换土层厚度变化,从而影响计算精度；在基坑支护结构设计中,采用改进等效代换土层厚度法来考虑车辆荷载影响是可行的。

交通荷载；基坑支护；改进等效代换土层厚度法；稳定性

1 概述

随着经济社会发展，交通量日益增加，且车辆荷载也日益加大。已有研究表明，车辆荷载是变频率、变振幅、长周期的不规则循环荷载[1]，车辆荷载对岩土变形与失稳都有其特殊性和复杂性。黎冰等[2]人将车辆荷载简化为集中静荷载，应用Boussibesq解和分层总和法分析得出车辆荷载的影响深度在6.0～8.0 m的范围；叶四桥等人[3]结合算例研究发现对于公路从滑坡下滑段通过的浅层滑坡，不考虑汽车荷载同考虑汽车移动恒载相比，稳定性系数要高4.3%～11%，不考虑汽车荷载比同时考虑汽车动荷载时稳定性系数要高5.8%～12.1%。

目前对车辆荷载的研究主要侧重于桥梁、道路两个方面，而对基坑支护结构影响研究甚少。众多学者通过对基坑的监测以及分析[4-5]，得出车辆荷载对基坑支护结构的影响也日益凸显。张向东等[5]通过改变影响基坑稳定性的交通荷载系数及支护结构相关参数，用数值模拟方法得出各参数改变与支护结构变形之间的关系，发现交通荷载作用产生的静载对支护结构影响较为明显，其中车辆载重和交通量的影响较为显著。刘素锦等人[6]在考虑车辆荷载对基坑支护结构的影响时，采用等效的方法将车辆荷载考虑为等效均厚土层和集中荷载，探讨了规范中常采用3种轮组对基坑支护结构稳定性的影响，但是其并未考虑车辆荷载作用时会引起支护结构周围土体破裂角变化的问题，而破裂角变化也会引起破坏棱体宽度变化，从而导致计算得到的等效厚度不准确。

本文在已有研究成果基础上，参考规范[7-8]，考虑车辆荷载作用时土体破裂角变化问题，计算得到等效代换土层厚度，并分析车辆荷载对基坑支护结构的影响。

2 计算方法

2.1 规范方法

文献[7-8]中指出，公路挡土墙背后填土面上作用有车辆荷载时会加速挡土墙破坏。挡土墙后的破裂体被视为一个滑移体，对作用在该滑移体上的车辆荷载常用等效代换土层厚度法进行换算，车辆荷载换算计算如图1所示，其厚度h0按下式计算

(1)

式中，γ为墙后填料的容重，kN/m3；B为破坏棱体宽度，m；L为挡土墙计算长度，m；∑Q为布置在B×L面积内的车轮总重，kN。

挡土墙计算长度按规范[7-8]规定选取，各级汽车荷载的重车，按式(2)计算：

(2)

式中，L0为前后轴距加轮胎着地长度或履带着地长度，m。L0按表1确定。

表1 L0的取值 m

图1 车辆荷载换算计算图示

2.2 改进方法

上述规范方法在未考虑车辆荷载的情况下计算出破裂角，由破裂角算出分布宽度，再在此分布宽度范围内布置车辆荷载，换算成均布土层厚度。但实际上由于在原路面上增加了等效代换土层厚度，其破裂角已经发生改变，而改变的破裂角影响荷载的分布区域，必然会引起计算误差增大，所以该方法有其局限性。

基坑支护结构与挡土墙有一定的区别，但是可以把基坑支护影响区域看成一个大的挡土墙来考虑。同时，在规范规定方法的基础上，利用改进等效土层厚度法来换算车辆荷载[9]，进而分析换算后的土层对基坑支护结构的影响。

首先，需要确定荷载面积，而此面积是以荷载宽度和长度的乘积来计算。第一步要在没有车辆荷载的情况下，运用库伦土压力理论，采用极限平衡法相关公式来求取破裂角。再根据破裂角算出荷载宽度B0，其表达式为

(3)

在初步确定的荷载宽度B0上按设计要求的车辆荷载等级布置轮组，即可计算出初步土层厚度h1。第二步由初步的h1重新计算破裂角θ，其表达式为

(4)

用荷载宽度B1再重新布置轮组，又可算出新的土层厚度h2，最后再根据设计要求的精度即θn-1与θn的误差限制在设定范围内，既可确定土层厚度hn作为最不利状态的设计值。其表达式为

(5)

式中，γ为填料容重；φ为填料内摩擦角；θ为棱体破裂角；a为挡土墙顶部填料高度；h为挡土墙高度；hi为等效代换土层高度；Bi为车辆荷载分布宽度(破坏棱体宽度)。

2.3 破裂角的求取

在库伦土压力理论中，根据库伦土压力计算简图(图2)，得到墙背对土体的反力

(6)

式中，ψ=φ+α+δ，其中φ、α、δ分别为填土的内摩擦角、墙背倾角、墙土间的摩擦角。

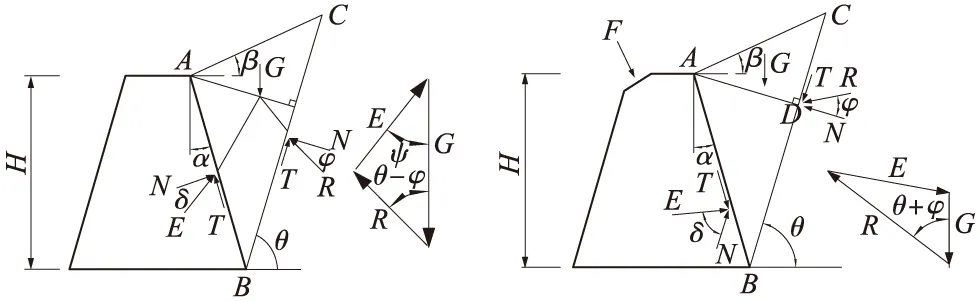
图2 库伦土压力计算简图

为了计算滑动土体即破裂棱体AC的长度，须求得最危险滑动面BC的倾角θ。而对于本文，填土面AB为水平面，α=0，此时，令dE/dθ=0，得出θ的计算公式

(7)

在车辆荷载的作用下，破裂面跟路基相交位置的不同会出现不同的作用形式，如图3所示，根据实例可以确定破裂面的边界条件，进而可以计算出其破裂棱体的自重

(8)

其中，A0、D0为边界条件系数。

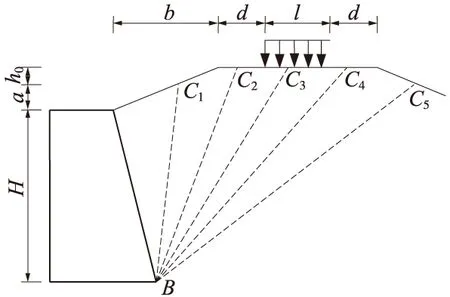
图3 不同边界条件的计算图示

破裂面交于荷载内侧时

(9)

破裂面交于荷载中部时

(10)

破裂面交于荷载外侧时

(11)

式中，h0为荷载换算的土层厚度；l0为车辆荷载的横向分布长度；b为边坡水平宽度(竖直基坑，b=0)。

将式(8)代入式(6)得到

(12)

令dE/dθ=0，得到下式，再据此换算成为实时的破裂角θi

(13)

3 工程实例

白苍岭(衡阳西)站为南宁市轨道交通1号线的第10座车站。车站位于衡阳西路上，呈东西走向布置。车站总长192.5 m，标准段宽19.7 m，底板主要坐落在粉质黏土及黏土层中。车站标准段开挖深度16.0～18.6 m，北端盾构井段深约10.8 m，南端盾构井段深约11.1 m。根据地质资料，基坑开挖范围内的土层条件见表2。

表2 各层土物理力学参数

基坑围护结构采用地下连续墙加内支撑的围护方案，地下连续墙厚度为800 mm。车站标准段基坑从上到下，第1道支撑为800 mm×800 mm混凝土(C30)支撑，第2、3道支撑均为钢支撑(外径609 mm，壁厚16 mm)，分别在0、-3.5、-8.1 m处设置。基坑标准段围护结构剖面见图4。

图4 围护结构剖面(单位:mm)

3.1 车辆荷载换算

由于库伦土压力理论的假设是，墙后填土是理想的散粒体，没有考虑土的黏聚力，但是实际中填料往往是用黏性土，对于本文研究的基坑开挖场地，地层情况更加复杂，此时引入等效内摩擦角[10]。针对黏性土的特性，按照工程界常取内摩擦角φ=35°进行计算，本基坑可以看成竖直的挡土墙，取δ=1/2φ进行计算。

3.1.1 暂不考虑车辆荷载作用时计算破裂角

根据公式(7)计算初始破裂角θ0，

得到初始破裂角θ0=59.7°

初始破裂棱体宽度B0=10.84 m

挡土墙计算长度L=5.6+Htan30°=16.339 m，根据文献[7-8]，取L=10 m。此时，等效代换土层厚度为

h1=∑Q/γB0L=0.27m。

3.1.2 考虑车辆荷载作用影响时计算破裂角

当考虑车辆荷载作用时，土体的破裂角必然会发生改变，而变化后的破裂角也会引起破坏棱体宽度的变化，此时分布面积便发生了改变，应再次计算破裂角θ1。根据边界条件可知，对于本工程场地，破裂面交于荷载外侧，在该竖直基坑中a、b、α均为零，此时θ1按照公式(13)进行计算。经过计算得到此时的破裂角为θ1=60.2°；

破裂棱体宽度B1=10.6m；

等效代换土层厚度为h1=∑Q/γB1L=0.276m。

按照此方法反复迭代计算，直至收敛，最后计算得到破裂角θ=60.2°，等效代换土层厚度h=0.276m。

车辆荷载对周围建筑结构的影响主要有静载产生的竖向压力以及振动荷载，等效代换土层厚度法换算的荷载是车辆静载部分，而没有考虑车辆动荷载的影响。引入动荷载系数[11]来考虑车辆动荷载的作用，动荷载系数常规取值为μ=0.1～0.4，此时由振动荷载部分转换成的土层厚度取为h′=0.4h。车辆荷载的最终换算厚度为Δh=1.4h=0.386m。另一方面，在工程实际中，在基坑附近的车辆荷载会有相应的限速处理，振动荷载的影响会相应的减少，所以，针对不同工程实际情况，车辆动荷载的影响会有差异性。

3.2 结果分析3.2.1 稳定性分析

根据常规基坑稳定性计算方法，从整体稳定性、抗倾覆稳定性、抗隆起稳定性3个方面进行理论分析，将本文的改进方法与工程中常规取路面荷载为20kPa的情况和不考虑车辆荷载时的情况分别进行对比分析。

其中，整体稳定采用瑞典条分法进行验算；在深厚的软土层中，当基坑开挖深度较大时，则作用在坑外侧的坑底水平面上的荷载相应增大，此时就需要验算坑底土的承载力，承载力不足时可能会导致坑底土的隆起，故需进行抗隆起稳定性验算。参照普朗特尔(Prandtl)及太沙基(Terzaghi)理论分别进行抗隆起稳定性验算，计算结果如表3所示。

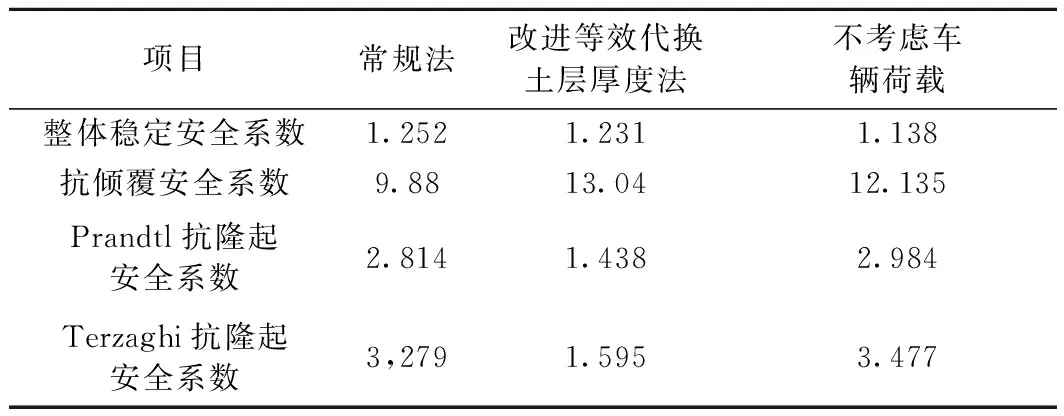
表3 安全系数

由表3可以看出，改进方法的整体稳定安全系数和抗倾覆安全系数略有增高，但增加幅度不大，而抗隆起安全系数略有降低，总体都在规范规定的范围之内，故均可满足工程要求。

3.2.2 墙体水平位移分析

结合实例，应用FLAC3D软件进行模拟分析。计算模型中，基坑左右边界范围取开挖深度的3～4倍，深度范围取开挖深度的2～3倍，故基坑左右边界分别取40 m，下边界取30 m，取7个地下连续墙槽幅进行分析，每个槽幅宽6 m，故模型尺寸为98.9 m(长)×42 m(宽)×30 m(高)。

土体单元采用Mohr-Coulomb本构模型，地下连续墙采用shell单元模拟，钢筋混凝土支撑及钢支撑均采用beam单元模拟。基坑边界条件假设为：基坑左侧、右侧和前后面方向水平约束，其他方向自由；土体底面为3个方向约束。通过模拟文中分析的3种情况，整理得到图5～图7的结果。

从图5看出，当开挖到4 m深时变形都相对较小，3种情况下变形趋势基本相同，主要是由于此时开挖深度较浅，侧压力相对较小，对支护结构影响相对较小。从图6中的变形曲线可以看出，随着开挖深度的加大，墙体向坑内的水平位移逐渐增大，变形幅度增加。利用3种方法得到的开挖变形曲线都呈现出两头小，中间大的“大肚形”变形特点，最大水平位移量随着开挖深度的增加而增大。采用常规的取路面荷载为20kPa进行计算时，最大水平位移相对较大，且最大水平位移点的位置相对较高；利用改进等效代换土层厚度法得到的墙体最大水平位移发生位置略有下移。

由图7可知，当开挖至11.1 m时，随着开挖深度加深，变形加大，最大水平位移点逐渐向下移动，开挖到坑底后，变形趋势减缓。由改进等效代换土层厚度法得到的墙体最大水平位移值比常规方法得到的略大，但增加幅值却相对较小，在可控的范围之内。当基坑深度在10 m以下时，水平位移的变化规律基本一致，主要原因在于地面超载对基坑的影响深度是有限的，在基坑较深的位置，地面超载对支护结构的影响已十分微小。

结合上述分析，本文引入的改进等效代换土层厚度法对基坑支护结构的影响与常规方法作用相似，故在考虑车辆荷载作用时，改进等效代换土层法仍有较好的适用性。

图5 开挖至4 m工况变形曲线

图6 开挖至8.6 m工况变形曲线

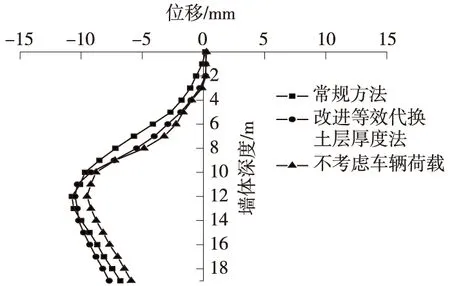
图7 开挖至11.1 m工况变形曲线

4 结语

(1)引入改进等效代换土层厚度法能有效解决土层厚度改变而引起破裂角变化的实际问题，在基坑支护结构设计中，采用改进等效代换土层厚度法来考虑车辆荷载影响是可行的，并为在基坑工程中如何考虑车辆荷载提出一个新的计算思路。

(2)由于车辆荷载的作用深度有限，基坑相对较深时，车辆荷载对深基坑的底部影响较小，故用本文提出的改进等效代换土层厚度法来考虑车辆荷载对特大深基坑的作用时，其影响相对较小。

(3)本文理论是根据墙后土体滑动楔块处于极限状态下的静力平衡导出的计算公式，而挡土墙所受土压力的大小与基坑支护墙体的高度、粗糙度以及填土表面形状等因素也有关系，有些影响因素未作考虑，仅从车辆荷载对基坑的影响进行重点分析。

[1]樊秀峰，简文彬.交通荷载作用下边坡振动响应特性分析[J].岩土力学，2006，27(S):1197-1201.

[2]黎冰，高玉峰，魏代现，等.车辆荷载的影响深度及其影响因素的研究[J].岩土力学，2005，26(S):310-313.

[3]叶四桥，唐红梅，肖盛燮，等.汽车荷载对滑坡稳定性的影响分析[J].重庆建筑大学学报，2006，28(5):106-109.

[4]石钰锋，宁锐，张学民，等.列车动载影响下偏压地铁基坑稳定性分析[J].铁道标准设计，2009(12):96-98.

[5]张向东，张晨光，刘家顺.交通荷载作用下深基坑支护结构稳定性分析[J].中国地质灾害与防治学报，2011，22(2):125-129.

[6]刘素锦，郭明伟，李兆源，等.浅析车辆荷载对深基坑支护结构的影响[J].地下空间与工程学报，2009，5(1):105-108.

[7]中华人民共和国交通运输部.JTG D30—2004公路路基设计规范[S].北京：人民交通出版社，2004.

[8]中华人民共和国交通运输部.JTG D60—2004公路桥涵设计通用规范[S].北京：人民交通出版社，2004.

[9]王来福.汽车荷载作用下挡土墙土压力计算方法的改进[J].中国海洋大学学报，2005，35(5):827-829.

[10]罗刚.等效内摩擦角及其在高挡土墙设计的运用[J].工业建筑，1997，27(6):37-42.

[11]曹源文，梁乃兴，于清，等.路面不平整引起的车辆动载计算方法[J].交通运输工程学报，2008，8(2):69-73.

Analysis of the Influence of Vehicle Load on Deep Excavation Supporting Structure

TANG Li-yun, QIU Pei-yong, YE Wan-jun, YANG Geng-she

(School of Architecture and Civil Engineering, Xi’an University of Science & Technology, Xi’an 710054, China )

In order to analyze the influence of vehicle load on deep excavation supporting structure, the conventional equivalent thickness of soil layer method is introduced, and the problem of the change of rupture angle caused by vehicle loads is addressed, and an improved method is introduced to solve this problem. The deadweight of rupture mass is calculated according to Coulomb’ s earth pressure theory. The convergence value of rupture angle is obtained by means of circulative iteration with reference to the equilibrium relation where the rupture mass keeps an equilibrium state, and the thickness of the new soil layer is calculated based on the rupture angle. In the light of the foundation pit of metro station in a city, and the influence of a conventional method and the improved equivalent layer method on supporting structure are compared by simulation, and the curves of horizontal displacements are obtained. The results indicate that the change of rupture angle will cause the change of the equivalent thickness of soil layer, and, as a consequence, the calculation accuracy is affected. It is applicable to employ the improved equivalent thickness of soil layer method to address the influence of vehicle load..

Vehicle load; Deep excavation supporting structure; Improved equivalent thickness of soil layer method; Stability

2014-10-27

陕西省重点科技创新团队计划(2014KCT-30)；陕西省科技统筹创新工程(2011KTZ03-02-01)

唐丽云(1977—)，女，副教授。

1004-2954(2015)08-0122-05

TU443

A

10.13238/j.issn.1004-2954.2015.08.026