基于几何与数学特征的人脸识别
梁奔香 蔡晓东 朱利伟
(桂林电子科技大学,广西 桂林 541004)
基于几何与数学特征的人脸识别
梁奔香 蔡晓东 朱利伟
(桂林电子科技大学,广西 桂林 541004)
提出了一种新的基于几何与数学特征相融合的人脸识别算法,分别提出了眉毛几何特征、人脸个性几何特征以及数学特征在人脸比对时的比对策略,采用打分的机制记录特征比对的结果。为了融合几何与数学特征,提出了基于权值的几何特征与数学特征的融合策略。实验结果表明,采用几何特征与数学特征相融合进行人脸识别比使用单一人脸特征进行人脸识别时有更高的识别率。
人脸识别;几何特征;数学特征;融合策略
1 引言
在过去的二十多年里,人脸识别得到了广泛的关注,很多人脸识别算法相继被提出,如主成分分析法(PCA)0、线性判别分析(LDA)0、二维的PCA方法0以及局部二元模式(LBP)0等基于人脸数学特征的方法,还有利用人脸各器官的位置、角度以及比例等几何关系的基于人脸几何特征的方法0。
为了能够充分利用人脸的特征进行人脸识别,本文提出了几何特征与数学特征相结合的人脸识别算法。整个系统框图如图1所示。

图1 几何特征与数学特征融合人脸识别框图
2 人脸特征提取
2.1 眉毛几何特征提取
眉毛是人脸的一个重要组成部分,它具有鲜明的轮廓,且其特征简单,易于提取。眉毛也是人脸和一个重要的生物特征,它相对于眼睛、嘴巴等人脸器官,更具稳定性和个体差异性,已经初步被证明可用于生物特征识别000。
为了能够反映眉毛的外观几何特征,本文提出了基于眉毛几何特征的眉毛模型,该模型可以用来直观地描述眉毛的外观形状。本文的方法是针对正脸的单边眉毛作处理的,眉毛图像统一归化大小为80*30的尺寸。首先通过阈值化和Blob分析得到归一化的眉毛二值图像,然后再根据得到的二值图像计算眉毛模型的各种几何参数,如眉毛的面积、长度、平均宽度、弯曲程度等,如图2所示。
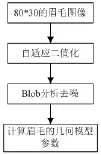
图2 眉毛几何模型参数计算流程图
2.2 人脸个性几何特征提取
每个人的脸型都有自己独特的特征,这些独有的特征称为人脸的个性特征,人脸器官等特征点的位置关系之间的差异,构成了人脸的个性几何特征。首先采用ASM算法0对人脸进行特征点定位,各个特征点的定位如图3所示。

图3 人脸特征点示意图
定位得到人脸特征点之后,接下来就是计算人脸的个性几何特征。首先计算某些关键特征点之间的欧氏距离,欧氏距离的计算公式如式(1)所示。
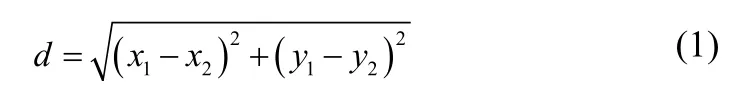
式(1)中,(x1, y1)、(x2, y2)分别表示两个特征点坐标,d表示这两个特征点的欧氏距离。根据欧氏距离的计算公式,所计算的特征点之间的距离如表1所示。

表1 所计算的特征点的距离
根据表 1所列出的特征点的距离,本文选取一些距离的比值作为人脸的个性几何特征,所选取的比值如表 2所示,表中列出了8个距离的比值即为人脸个性几何特征。
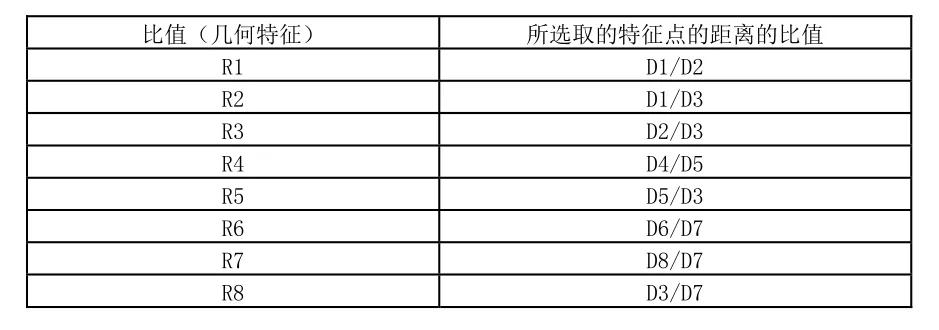
表2 人脸个性几何特征列表
2.3 人脸数学特征提取
人脸的数学特征包括人脸的LBP特征、PCA特征、Gabor小波等,本文以 LBP特征为例来说明人脸几何特征与数学特征相融合进行人脸识别的整个过程。
LBP处理过程如图3所示,在一个3*3大小的区域中,以中心像素点的灰度值为准,将它与周围的 8个像素点的灰度值进行比对,若周围的像素点的灰度值比中心点的小,则标记为0,否则标记为1。通过这样比对后,将周围的8个像素点的比较得到的结果按照顺时针连接,得到一个 8位的二进制数,将这个二进制数转换成十进制,所得的值即为这个中心点的 LBP值。遍历整个图像,即可计算出所有像素点对应的LBP值,将所有LBP值以图像的形式输出如图4所示。
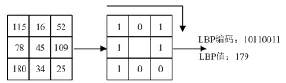
图3 LBP处理过程

图4 LBP处理后的图像
3 人脸特征比对策略
3.1 眉毛几何特征比对
前面介绍了眉毛几何特征的提取,一共提取了眉毛的 5个几何参数,这 5个参数分别是:眉毛区域的面积、长度、平均宽度、弯曲程度和走向趋势,两个眉毛进行比对就是这5个参数进行比对。两个眉毛的比对得分计算如下:
(1)两个眉毛中相同性质的参数(如长度、宽度等)相减并取绝对值得到两个对应参数的差异值d;
(2)取dmax为样本中不同个体间的差异的最大值,dmax的值通过眉毛参数统计得到,当五个参数的差异值d都小于或等于0.2dmax时,则计算相应的分数,否则直接赋予零分;
(3)对于差异值d在[0,0.2dmax]区间的,计算其比对的得分,得分的区间为[0,100],差异值d越大,得分越小,反之则得分越大,即分数与差异值d成反比例关系,d与分数(S)的关系如下图5,其表达式如式(2);
(4)将5个参数的比对得分相加,得到总分数;
(5)将总分进行归一化,使分数落在[0,100]区间上。
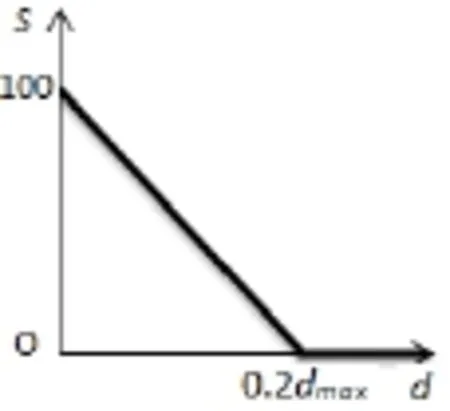
图5 分数S与差异值d的关系图

3.2 人脸个性几何特征比对
前面介绍了人脸个性几何特征的计算方法,共计算了 8个人脸几何特征,这 8个几何特征都是人脸上关键点(眼、口、鼻等)距离之间的比值使用比值作为人脸的几何特征。下面介绍两个人脸几何特征的比对得分策略。
设两个人脸的几何特征参数向量分别为R1、R2,表达式如式(3)、(4)。
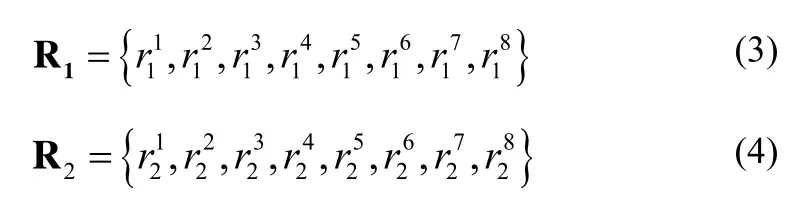
两个特征向量相减,取绝对值,得到特征差值向量D,如式(5)。
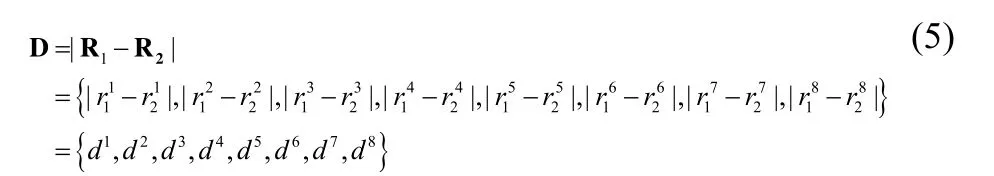
计算得到特征差异值向量D后,根据D向量中的值计算特征比对的得分。对于某一个特征,其差异值越大,赋予的分数应该越小,差异值越小则赋予更高的分数。为此,本文引入了一个指数减函数来计算两个几何特征比对时的得分,以两个特征的差异值d作为变量,以1/e(e=2.71828)为底数,其表达式如式(6)所示,曲线图如图6所示。
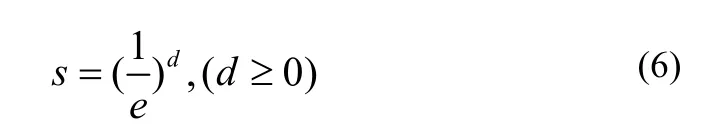

图6 指数函数曲线图
对人脸个性几何特征的 8个参数都作相应的比对得分处理,然后将8个参数的比对得分相加如式(7)所示。计算所有参数的得分总和后,将得分进行归一化处理,使分数映射到[0,100]区间上,如式(8)所示。
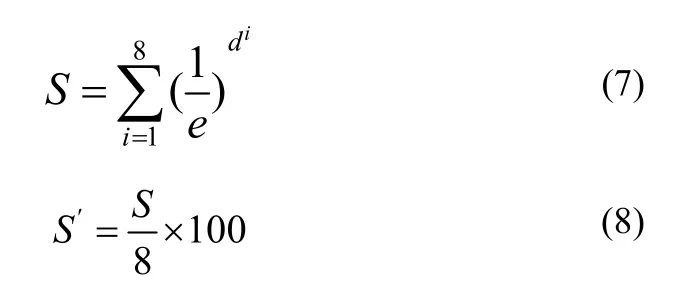
3.3 人脸数学特征比对
对人脸图像进行LBP处理得到LBP特征图像后,通过比较 LBP图像的灰度直方图来衡量人脸图像之间的差异程度。LBP图像直方图如图7所示。
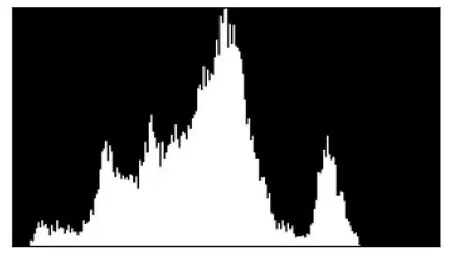
图7 LBP图像直方图
每个灰度直方图都是一个包含 256个元素的一维向量,采用卡方距离来比较两个向量的相似性,卡方距离的计算公式见式(9)。计算得到的卡方距离越小,说明这两个向量的相似度越高。
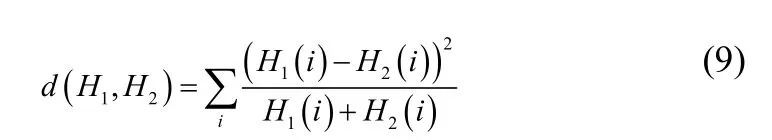
将计算得到的卡方距离进行升序排序,按照其排名的名次进行赋分,得分的大小在[0,100]之间,第一名赋予最高的分数,最后一名赋予最低的分数,其他位置的则根据其相应的名次赋予相应的分数,计算公式如(10)所示。这样就得到数学特征的比对得分。
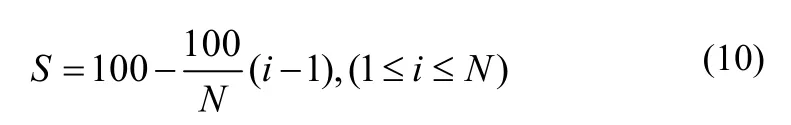
式(10)中,N表示训练样本总数,i表示对应样本的卡方距离排名的名次,其取值在[1,N]区间中。
4 几何特征与数学特征融合策略
几何特征与数学特征在人脸识别时的作用大小是不相同的,为此,本文提出了权值的特征融合策略,即不同的特征将赋予不同的权重。根据前面人脸几何特征和数学特征的比对得分结果,按照不同的权值将这些分数进行相加即为最终的人脸比对得分。
设S1、S2、S3分别表示眉毛几何特征比对得分、人脸个性几何特征比对得分以及人脸数学特征比对得分,w1、w2、w3分别表示这三种特征的分数融合时的权值,则最终的得分S如式(11)计算得到。
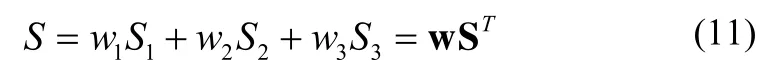
其中w={ w1,w2,w3},S={ S1,S2,S3},分别表示权值向量和分数向量。
5 实验结果与分析
5.1 实验数据库
本文采用了东方人脸数据库(OFD full DB labeled)作为实验数据库,选取不同光照条件下的人脸图像进行实验。在实验过程中,选取每人 5张不同光照条件下的人脸图像作为训练样本库,部分训练样本的人脸图像如图 8所示。所有的人脸图像都缩放到200*250的分辨率。实验中采用VS2008 和OpenCV图像处理库编程进行实验。

图8 部分训练样本人脸图像
5.2 实验结果与分析
首先计算人脸比对时人脸各部分特征比对时的得分,S1、S2、S3分别表示眉毛几何特征比对得分、人脸个性几何特征比对得分以及人脸数学特征比对得分。测试的输入样本以及与之比对的训练库部分样本图像如图9、10所示,计算得到S1、S2、S3的分数如表3所示。

图9 输入测试样本人脸图像
图10 训练样本中部分人脸图像
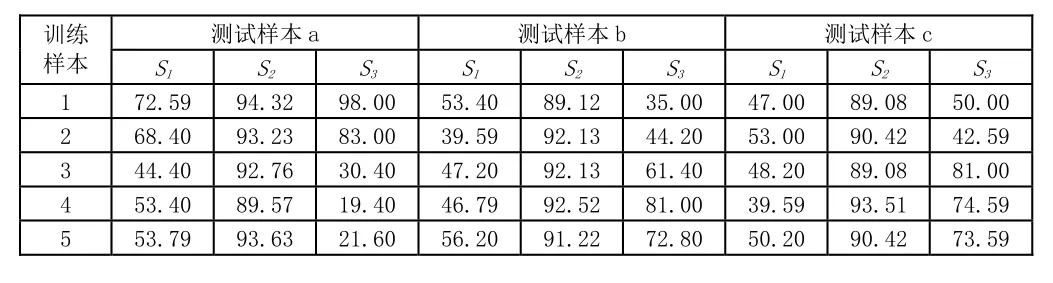
表3 测试样本与训练样本比对得分结果
使用几何特征数学特征进行人脸识别实验,实验中测试了87个人,每个人包含5张训练人脸图像,一张测试人脸图像。实验中测试了数学特征与几何特征不同权值下的人脸识别率。实验结果如下表4所示,w1、w2、w3分别表示眉毛几何特征、人脸个性几何特征以及人脸数学特征融合时的权重。
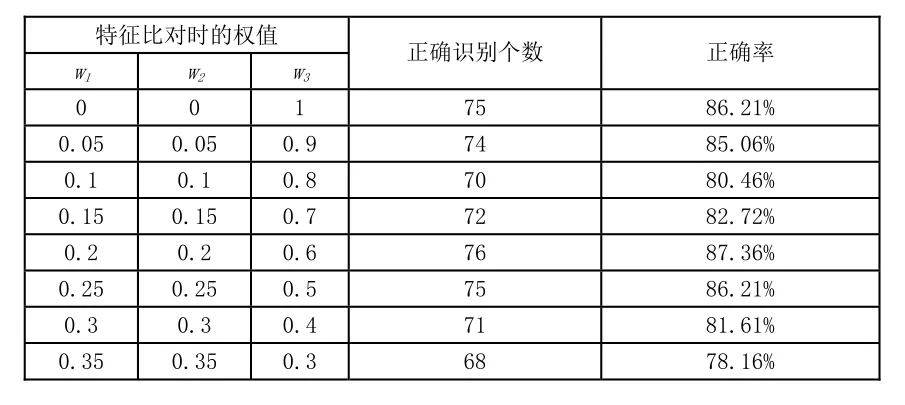
表4 几何特征与数学特征融合的人脸识别结果
从表 4可以发现,单纯使用数学特征进行人脸识别时(w1=0、w2=0、w3=1),正确识别率为 86.21%。刚开始引入几何特征时,即几何特征的权值不为零时,由于几何特征的权值较小,使得人脸识别正确率有所下降,逐渐增大几何特征的权值,人脸识别率也逐渐上升,当w1=0.2、w2=0.2、w3=0.6时,人脸正确识别率达到最大87.36%,随着几何特征权值的继续增大,人脸正确识别率又逐渐降低,当单纯采用几何特征进行人脸识别时,识别率很低,可以说基本不具备人脸识别的能力。实验表明,在人脸识别过程中,人脸的数学特征占有主导地位,当几何特征和数学特征的占有比例(权值)设置合适时,能够获得较高的人脸识别率,超过了单纯使用数学几何进行时人脸识别时获得的识别率。
6 结论
本文提出了一种新的基于人脸几何特征与数学特征相融合的人脸识别算法,首先提取人脸的眉毛几何特征、人脸个性几何特征以及人脸的数学特征。然后分别提出了眉毛几何特征、人脸个性几何特征以及数学特征在人脸比对时的比对策略,采用打分的机制记录特征比对的结果。最后,为了融合几何与数学特征,提出了基于权值的几何特征与数学特征的融合策略。实验结果表明,采用几何特征与数学特征相融合进行人脸识别比使用单一人脸特征进行人脸识别时有更高的识别率。在人脸几何特征与数学特征相融合的人脸识别算法中,本文采用人为的设置几何特征与数学特征的权值,设置的权值并不一定就是最佳的权值,能否找到一种自动地计算各个特征的权值,使得各个特征的权值是最优的,这有待深入研究。
[1]Turk, M., & Pentland A.. Face Recognition Using Eigenfaces[J]. IEEE,1991:586-591.
[2]Belhumeur P. Eigenfaces vs. Fisherfaces:Recognition Using Class Specific Linear Projection [J]. IEEE Trans. on Pattern Analysis and Machine Intelligence, 1997,19(7).
[3]Jian Yang, Zhang D.,Frangi,etal. "Two- dimensional PCA: a new approach to appearance- based face representation and recognition [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on,2004,26(7):131, 137.
[4]T. Ahonen, A. Hadid and M. Pietikainen. Face Recognition with Local Binary Patterns[C]. In Proceedings of the 9th European conference on computer vision, Berlin Heidelberg, 2004:469-481.
[5]Xu Yuan. A Research on Face Recognition Method based on Geometric Features[D].China University of Geosciences for Master Degree,2008.
[6]J. Sadr; L. Jarudi; P. Sinha. The role of eyebrows in face recognition[J].Perception,2003,(32):285-293.
[7]李玉鑑,付翠花.一种基于特征串比较的眉毛识别方法[J].北京工业大学学报,2008,34(1):103-108.
[8]李玉鑑,李星立.基于离散 HMM 的眉毛识别方法研究[J].中国图象图形学报,2008,13(8):1465-1469.
[9]T Cootes,D Cooper,C Taylor,et al. Active Shape Models-Their Training and Application[J].Computer Vision and Image Understanding,1995,61(1):38-59.
Face recognition based on geometric and mathematics features
Presents a new face recognition algorithm based on geometry and mathematical characteristics. The contrast strategy of the geometric feature of eyebrows, face personality geometry characteristics and the characteristics of mathematics were put forward. A weight scoring mechanism was used to record the comparison results of characteristics. In order to fusion with the facial geometric features and mathematical characteristics, a fusion strategy of the weights was proposed based on the geometrical characteristics and mathematical characteristics. The experimental results show that the geometric feature and the integration of mathematical characteristics for face recognition has higher recognition rate than using a single face feature for face recognition.
Face recognition; geometric feature; mathematical characteristics; fusion strategy
TP391.4
A
1008-1151(2015)05-0013-04
2015-04-13
桂林电子科技大学研究生科研创新项目(GDYCSZ201410)。
梁奔香(1987-),男,广西贵港人,桂林电子科技大学硕士生,研究方向为研智能视频图像处理。

