ZL50装载机换档过程动力学数值模拟*
尹汉桥
(中国煤炭科工集团太原研究院,山西太原 030006)
0 引言
ZL50装载机的换档过程是一个复杂的过程,是随时间变化的动态过程,变速箱传动系统及整机设计时,要研究其换档过程中各构件的运动参数及动力参数的变化规律[1]。借助计算机对ZL50装载机的换档过程中各参数的变化规律进行模拟研究,在某种程度上可以替代价格昂贵的试验[2]。
研究ZL50装载机换档瞬时过程,建立变速箱的运动数学模型,即运动微分方程是关键。行星变速箱换档过程比较复杂,特别是多自由度行星变速箱,每换一个档位,就是一种新的运动关系,需要重新建一次数学模型。
以下方法是一种计算机生成任意自由度行星变速箱运动微分方程的方法。用数值方法解微分方程,可以对ZL50装载机的换档过程进行动态仿真,进而深入研究ZL50装载机的换档过程。
1 转速关系及结构表示
通常行星变速箱用传动方案简图表示,计算机又不具备识别图形的功能。以下方法,可以便利地将变速箱结构在计算机中表示,并在计算机中以数字的形式存储下来[3]。
把太阳轮、行星架、齿圈、输入轴、输出轴、制动器及离合器的两摩擦盘称为运动件,运动件总数:
P=z+3x+2t+2式中:z、x、t分别为制动器数、行星排数和离合器数;几个运动件固联并具有通一速度的运动体称为构件。每个运动件都包含在构件中,而且只属于一个构件。
如果某个构件含有k个运动件,这k个运动件转速相等,对应k-1个转速方程。如果行星变速箱有q个构件,就有P-q个转速方程。设变速箱自由度为f,则:
q=x+f
变速箱的一个行星排又对应一个方程:ωs+αωr-(1+α)ωc=0式中:ωr、ωs、ωc分别为齿圈、太阳轮、行星架转速,α等于齿圈半径除以太阳轮半径。x个方程对应x个行星排。根据上面分析,行星变速箱有:
n=P-q+x=P-(f+x)+x=P-f个方程。
图1是ZL50装载机二自由度行星变速箱结构简图,共有4个构件,12个运动件。其中1,3,6,11四个运动件包含在构件Ⅰ中,可以写出三个方程:
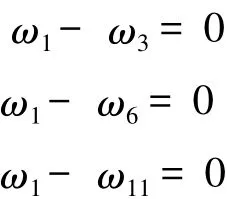

图1 ZL50装载机行星变速箱结构简图
同样方法可以写出构件II、III、III的独立方程。所有方程一起联立写成:

式(1)为变速箱转速方程,其中:An为行星变速箱转速矩阵;ω为转速向量。若设α=2,则:

2 二自由度行星变速箱动力学模型
2.1 构件转速表示
前面提到,n-f个方程是独立的,如果f=2转速矩阵An可化为以下形式:

用 ωn-1,ωn表示其余运动件的转速,即:

2.2 转动惯量矩阵
行星变速箱运动过程中,位能的影响很小,因而适合拉格朗日能量方程[4]:

式中:T为系统的总动能;ωl为广义角速度;Fl为分系统广义动能:

式中:Ti为第 i个构件的动能,Ti=Jiωi2/2;Lj为第 j个行星排行星轮个数;Tj为第j个行星排单行星轮的动能。如果用ωn-1和ωn表示第第i个构件的转速,则动能:


则第j个行星排的行星轮转速为:

设行星轮质量为mpj,转动惯量为Jpj,则行星轮的动能为:

总动能式(4)为:


式中:

对式(5)求导:
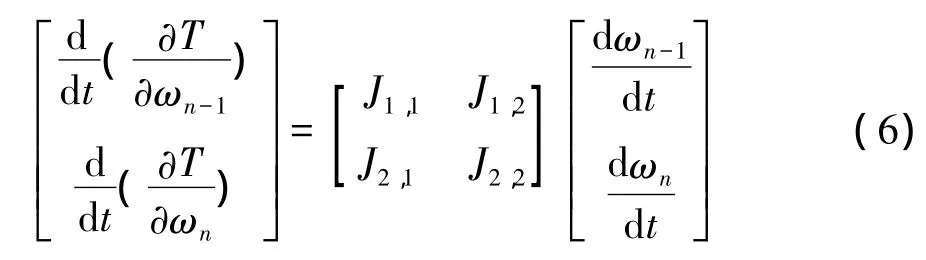
2.3 外力矩表示
行星变速箱所受外力矩有:制动器、离合器的摩擦力矩;输入、输出转矩。
主动盘摩擦片滑摩力矩做负功,从动盘摩擦片滑摩力矩做正功;制动器摩擦片摩擦力矩做负功;输入轴上的力矩做正功;输出轴上的阻力矩做负功。在行星变速箱上有h=2+z+2t个外力矩作用,其中第k个外力矩对应的运动件转速与独立运动件转速的关系为:

相应微位移:

外力矩做的元功:


其中:k=1,2,……,h
注意到式(7)右边的后半部分为式(3)右边广义力矩:
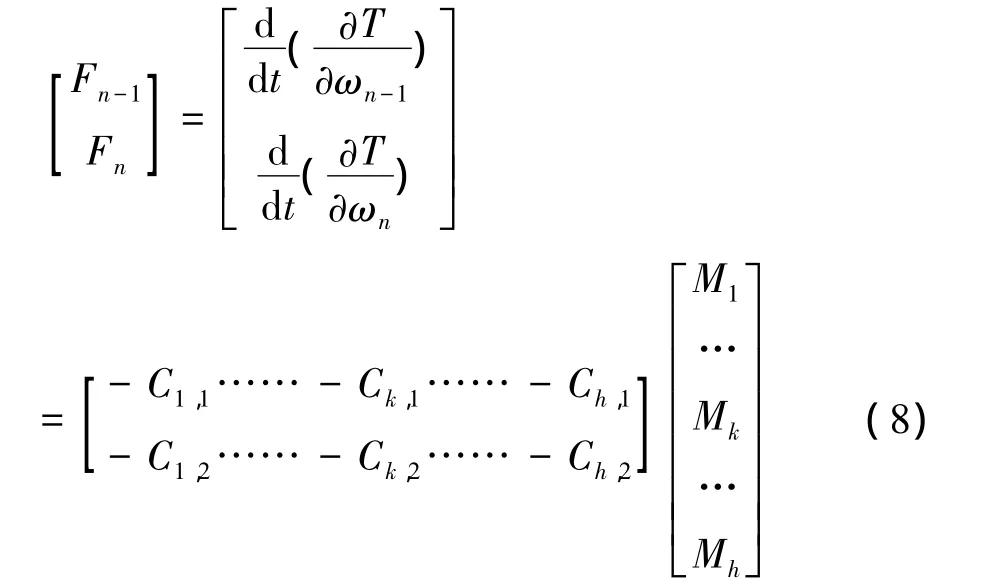
式(6)和式(8)组合得到变速箱运动微分方程:
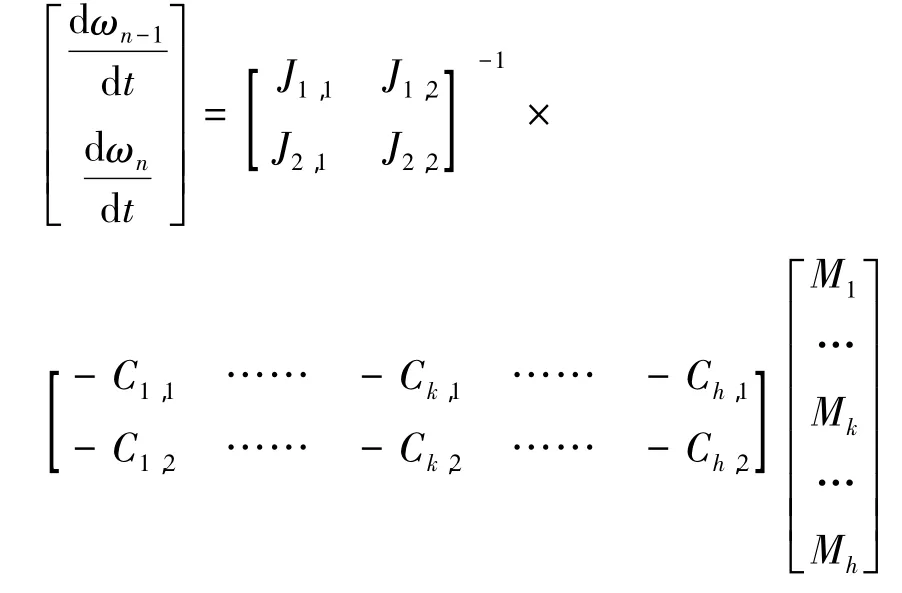
3 ZL50装载机换档过程数值模拟
对国产ZL50轮式装载机变速箱进行数值模拟。图1所示的结构简图,工况为:
由Ⅰ档行走换为Ⅱ档行走(松开制动器10,接合离合器11、12),操纵油压按线性规律上升。变速箱输入转矩:M1=736 N·m;输入转速ω1=16.2 r/s;输出轴上的阻力矩M2=687 N·m;输出轴速度ω2=5.1 r/s。
表1是ZL50装载机变速箱换档离合器相关尺寸参数;表2为行星变速箱各构件转动惯量。数值计算结果曲线如图2所示。

图2 计算离合器参数变化曲线图
如表1所列,方案1方案3均满足应力分析要求,其中方案1产生最大应力部位位于水平板焊接处的中间筋板,方案3位于与法兰焊接处的筋板上,考虑日后可修复性,旋转方案作为优化设计方案。

表1 不同设计方案下回转台底座应力分析
4 结语
通过对大包回转台回转底座5种工作条件下受力载荷情况进行系统分析,查找出能造成底座裂纹主要的原因为螺栓连接受冲击载荷造成受力不均,结合该种状况,选择在不干涉连接条件情况下,采用原设计回转台底座与回转台底座连接件优化设计,取消螺栓连接,同时优化设计筋板,提高法兰连接强度。同时采用有限元分析,对3种筋板条件下大包回转台冲击载荷对于回转载荷冲击载荷情况进行对比,选择最优设计方案,提高了设备运行安全系数。
[1] 汪海涛.冶金机械设计手册[M].北京:北京科技出版社,2006.
[2] 张剑寒,方 刚,黄其明.新型转炉系统整体结构三维有限元分析[J].计算机辅助工程,2009,18(3):27-30.

