半线性映射的性质

梁美花 王凤娟 吴开迅 卢家宽

（广西师范大学数学与统计学院，广西 桂林 541004）

半线性映射的性质

梁美花 王凤娟 吴开迅 卢家宽

（广西师范大学数学与统计学院，广西 桂林 541004）

文章给出半线性映射的一些基本性质，研究半线性变换与线性变换之间的联系，特别地给出了它们等价的一个充分必要条件。

线性空间；半线性映射；线性映射

高等代数是高等院校里数学专业的重要基础课程，也是目前大多数高校数学专业考研的必考科目之一。线性空间与线性变换是高等代数的重要研究对象，事实上，关于线性空间和线性变换的理论已经很成熟，内容也很丰富，可参考文献[1]。因此，研究与线性空间与线性变换相关的课题显得很重要，也具有理论基础。例如，文献[2]研究了p-半线性映射的若干性质。

文献[1]第301页第36道练习题中提到线性变换的如下推广：

定义1 设F是一数域，V,W是F上线性空间，f是V到W的映射，称f是V到W的半线性映射，如果对任意的α,,有

V到W的所有半线性映射的集合记为QF(V,W).

特别地，V到自身的半线性映射称为V的半线性变换.这时，QF(V,V)简记为QK(V) .

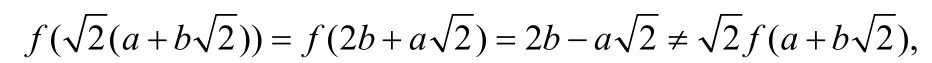
从上面的例子已经可以看出，半线性映射的概念比线性映射的概念具有更广泛的普遍性，因而，它的应用范围也更广。首先，关于半线性映射有如下基本性质：

性质1 设F是一数域，V,W是F上线性空间，f是V到W的半线性映射，则有

（1）(0)0f=.

证明

类似线性映射的加法、乘法, 可以定义半线性映射的加法、乘法。

定义2 设F是一数域，V,W是F上线性空间， f, g是V到W的半线性映射，k∈F, 对任意的α∈V, 规定

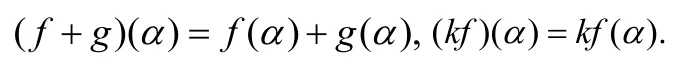
分别称为f与g的和，以及k与f的数乘。

笔者有如下两个命题：

证明 对,Vα β∀∈，有

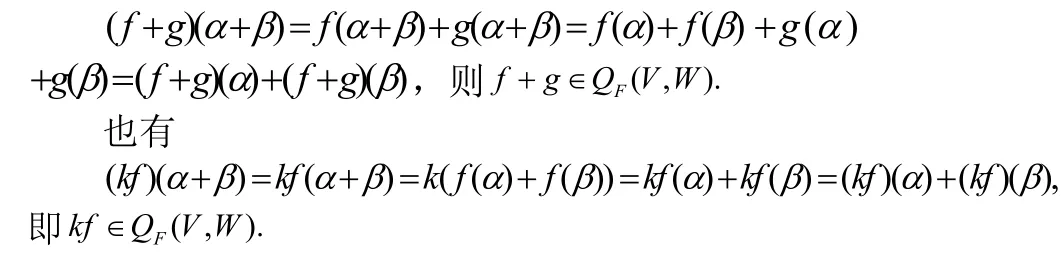
命题2 设F是一数域，QF(V,W)是F上线性空间，QF(V,W)关于上面定义1中的加法、数乘运算成为F上的线性空间。

证明 由于QF(V,W)对上面定义的加法及数乘运算封闭，要证Q (V,U)是线性空间，还需验证线性空间定义中的8条公理，即：

由例子 1知，在一般情况下，半线性映射不一定是线性映射。但下面的定理给出了半线性映射与线性映射等价的一个充分必要条件。

定理1 设F是一数域，V,W是F上有限维线性空间，则F=Q当且仅当

[1] 蓝以中.高等代数简明教程(第二版)上册[M].北京:北京大学出版社,2007.

[2] 王喜林,刘丽红,王波.p-半线性映射的性质[J].东北师大学报(自然科学版),2010,42(4):21-25.

The properties of semilinear mappings

In this paper, some elementary properties of semilinear mappings, in particular, a necessary and sufficient condition for a semilinear mapping to be linear mapping are given.

Vector spaces; semilinear mapping; linear mapping

O151.2

A

1008-1151(2015)10-0096-02

2015-09-10

广西高等教育教学改革工程项目(2014JGA116), 2015年自治区级大学生创新创业训练计划立项项目（201510602037）。

梁美花（1985－），女（壮族），广西师范大学学生；卢家宽（1980－），男（壮族），广西贵港人，广西师范大学数学与统计学院副教授，研究方向为群及其表示。