考虑后悔行为的具有二元期望的随机多属性决策方法

梁霞，姜艳萍

（东北大学工商管理学院，辽宁沈阳 110169）

（School of Business Administration，Northeastern University，Shenyang 110169，China）

考虑后悔行为的具有二元期望的随机多属性决策方法

梁霞，姜艳萍

（东北大学工商管理学院，辽宁沈阳 110169）

针对属性具有二元期望的随机多属性决策问题，提出一种考虑决策者后悔行为的决策分析方法.首先，根据随机决策信息和关于属性的二元期望信息，计算方案满足每个属性二元期望中目标价值的概率.然后，考虑到决策者的后悔心理行为，根据二元期望中的期望概率，计算方案关于每个属性二元期望的后悔-欣喜值.进一步地，根据方案关于每个属性的后悔-欣喜值，计算方案的综合感知值，并对方案进行排序.最后，通过一个风险投资的例子验证了该方法的可行性和实用性.

随机多属性决策；二元期望；后悔行为；排序

（School of Business Administration，Northeastern University，Shenyang 110169，China）

1 引言

随机多属性决策是指属性评价值为随机变量的有限方案选择问题，在经济管理等领域存在丰富的实际应用背景［1-3］.从众多传统随机多属性决策的研究成果看，大多数是以假设决策者完全理性为前提的.事实上，已有研究表明，在很多实际的决策过程中，决策者是有限理性的，常常具有一定的心理行为［4，5］.因此，研究具有决策者心理行为的随机多属性决策问题是一项具有理论价值和实际意义的课题.

近年来，关于考虑决策者心理行为的随机多属性决策问题已经开始得到许多学者的关注，并相继取得了一些研究成果.这些研究成果主要是基于前景理论的思想，具体地，根据方案的优选方法，又可细分为两类研究思路.第一类是通过集成方案关于各属性的前景值，来进行方案排序［6-11］，Hu等［6］针对考虑属性期望的动态离散型随机多属性决策问题，引入决策者的风险态度，提出了一种基于累积前景理论和集对分析的决策分析方法.胡军华等［7］针对准则权重完全未知、准则值部分缺失的随机多准则决策问题，引入了决策者的心理行为，提出了一种基于累积前景理论和随机加权法的决策方法.王坚强等［8］针对概率和属性值均为区间灰数、属性权系数不完全确定的灰色随机多属性决策问题，定义了区间灰数的排序方法及其前景价值函数，并考虑决策者的参照依赖和损失规避心理行为，通过构建规划模型确定最优权系数，根据综合前景值进行方案排序.张洁等［9］研究了决策矩阵信息所出现的随机概率形式，将随机概率转化为区间数信息，并提出了基于前景理论的方案排序方法.李鹏等［10］针对指标权重未知、方案的指标值为直觉模糊数的随机多指标决策问题，提出了新的直觉模糊相似度公式，并考虑到决策者的行为，提出了一种基于前景理论和直觉模糊距离的决策方法.张晓等［11］将前景理论的思想引入到随机多属性决策问题中，针对具有参考点的混合型决策问题，考虑到决策者的参照依赖和损失规避行为，提出一种新的决策分析方法.第二类是将随机占优和前景理论相结合，确定并集结前景占优度矩阵，来进行方案排序［12，13］，Tan等［12］针对属性具有期望水平的随机多属性决策问题，考虑到决策者参照依赖和损失规避等行为，提出了前景随机占优度的计算方法，得到一个方案占优于另一方案的程度，并提出了基于前景随机占优度的决策分析方法.张晓等［13］针对随机多属性决策问题，将具有随机变量的决策矩阵转化为关于参考点的收益和损失矩阵，依据前景随机占优准则判断两两方案之间的占优关系，并运用PROMETHEEII方法对方案进行排序.

以上研究成果的取得，极大地推动了考虑决策者心理行为的随机多属性决策方法的发展，但仍存在着一些问题需要进一步深入研究，例如，已有随机决策方法中涉及的决策者的行为还比较单一，即主要考虑了参照依赖和损失规避行为，这显然难以完全反映现实决策问题中复杂的决策行为.尤其需要指出的是，大量现实的随机多属性决策问题中，常常涉及决策者的后悔行为，即当决策者意识到或仅仅是想象到假如做出其它决定会使结果更好时，决策者对此前的决定会感到后悔，反之，会感到欣喜［14-16］.此外，已有研究中考虑的属性期望类型还不够丰富，主要考虑了决策者给出属性的一元期望，即要求方案的属性值满足某一特定的值，本文称为目标价值.事实上，在许多实际的随机多属性决策问题中，决策者有时会给出关于属性的二元期望形式［17］，即不仅给出属性值满足的目标价值，而且给出满足该目标价值的期望概率.例如，在客户服务部门服务质量评价问题中，客户希望电话在30s内被客服人员接通的概率不低于0.8，其中30s是二元期望的目标价值，0.8是期望概率［17］；又如在风险投资项目选择问题中，决策者期望投资项目的长期收益不低于20万元的概率至少达到0.7，并且越大越好，则（20，0.7）是关于长期收益这一属性的二元期望.更为重要的是，目前，关于考虑决策者后悔心理行为同时考虑属性具有二元期望的随机多属性决策问题的研究还几乎空白.鉴于此，本文考虑到决策者的后悔心理行为，针对属性具有二元期望的随机多属性决策问题，提出一种新的决策分析方法.在该方法中，首先提炼并描述出随机多属性决策问题中涉及的五种典型的二元期望形式，然后考虑到决策者的后悔规避行为，给出方案后悔-欣喜值的计算方法，进一步地，给出基于综合感知值的方案排序和择优方法.

2 问题描述

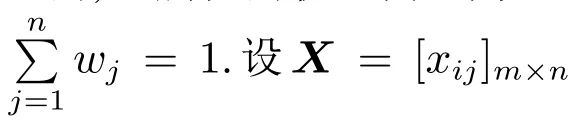
表1 决策矩阵XTable 1Decision matrix X

假设决策者给出关于属性的二元期望向量为T=（T1,T2,...,Tn）T.Tj=（tj,sj）为决策者给出关于属性Cj的二元期望，tj表示二元期望的目标价值，sj表示“满足”目标价值tj的期望概率.本文中“满足”目标价值具体包括“不低于”目标价值和“不高于”目标价值两种情形.根据期望概率sj的类型和数量，主要考虑以下五种二元期望类型：

1）单基点Ⅰ型二元期望.即属性值xij“满足”目标价值tj的概率至少达到sj，并且概率越大越好，其中0≤sj≤1.例如在风险投资中，决策者期望投资项目的预期收益不低于40万元的概率至少达到0.6，并且越大越好；

3）单基点Ⅱ型二元期望.即属性值xij“满足”目标价值的概率至多不超过sj，并且越小越好，其中0≤sj≤1.例如在风险投资中，决策者期望投资项目的投资成本不低于10万元的概率至多不超过0.6，并且越小越好；

4）双基点Ⅱ型二元期望.记期望概率为sj=,〉，即属性值xij“满足”目标价值tj的概率至多不超过，最好低于，并且概率越小越好，其中0≤＜≤1.例如在风险投资中，决策者期望投资项目的投资成本不低于8万元的概率至多不超过0.6，最好低于0.4时，并且越小越好；

5）区间型二元期望.即属性值xij“满足”目标价值的概率必须在,］之间，其中0≤＜≤1.例如在风险投资中，决策者期望投资项目的绿色能源市场份额不低于20个百分点的概率必须在［0.4,0.7］之间.

基于上述符号说明，本文需要解决的问题是，根据决策矩阵X=［xij］m×n，决策者关于属性的二元期望向量T和属性的权重向量W，考虑到决策者的后悔心理行为，提出一个有效的决策方法对备选方案进行排序和择优.

3 决策分析方法

在随机多属性决策过程中，对于属性给出二元期望信息的情形，决策者会将二元期望视为虚拟方案产生的结果，往往将备选方案的评价结果与二元期望进行比较，如果发现选择某方案会获得比期望更好的结果，决策者选择该方案时会感到欣喜，反之，会感到后悔.因此，基于这一思想，针对上述随机多属性决策问题，考虑属性的二元期望信息，具体的多属性决策方法描述如下.

3.1计算方案“满足”目标价值的概率

计算方案Ai关于Cj的属性值xij“满足”二元期望（tj,sj）中的目标价值tj的概率yij=Pr（xij≻tj），具体方法描述如下.

对于连续型随机属性值xij，xij“满足”目标价值tj的概率为

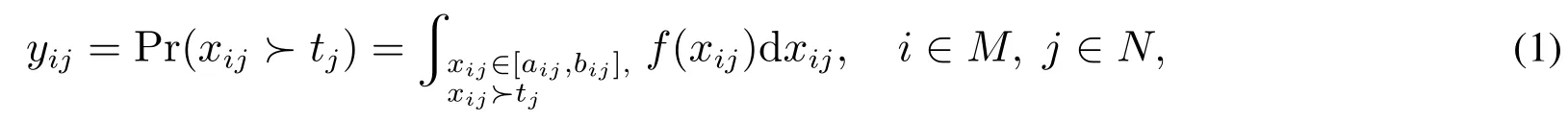
对于离散型随机属性值xij，xij“满足”目标价值tj的概率为

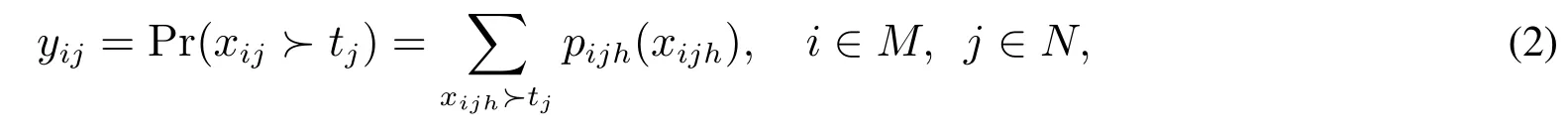
其中“≻”表示的含义是“满足”目标价值.例如，当决策者期望属性值xij分别为“不低于”或“不高于”目标价值tj时，“xij≻tj”分别表示“xij≥tj”或“xij≤tj”.

3.2 计算方案的后悔-欣喜值

考虑到决策者的后悔心理行为，根据方案“满足”Ai关于属性Cj的属性值xij“满足”目标价值tj的概率yij和期望概率sj，针对五种二元期望类型，计算方案Ai关于二元期望（tj,sj）的后悔-欣喜值dij.

1）针对单基点Ⅰ型二元期望，若yij＜sj，则方案Ai“满足”目标价值tj的概率yij没能达到决策者关于属性Cj的期望概率，此时决策者选择方案Ai会感到后悔；反之，若yij≥sj，决策者会感到欣喜.因此，利用Bell［19］和Chorus［20］提出的后悔-欣喜函数，方案Ai关于二元期望（tj,sj）的后悔-欣喜值为

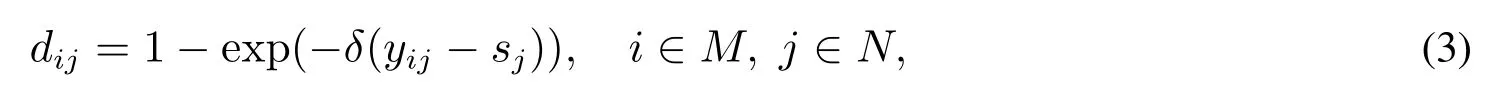
其中δ为决策者的后悔规避系数，δ＞0，δ越大，决策者的后悔规避程度越大.关于此类型的后悔-欣喜函数如图1所示.

2）针对双基点Ⅰ型二元期望，若yij＜，则方案Ai“满足”目标价值tj的概率yij没有达到决策者关于属性Cj的最低期望概率，此时决策者选择方案Ai会感到后悔；若yij＞，则yij达到决策者关于属性Cj的满意期望概率，此时决策者会感到欣喜；若≤yij≤，则yij达到决策者关于属性Cj的最低期望概率而没有达到满意期望概率，此时决策者既不会感到后悔也不会感到欣喜.因此，方案Ai关于（tj,sj）的后悔-欣喜值为

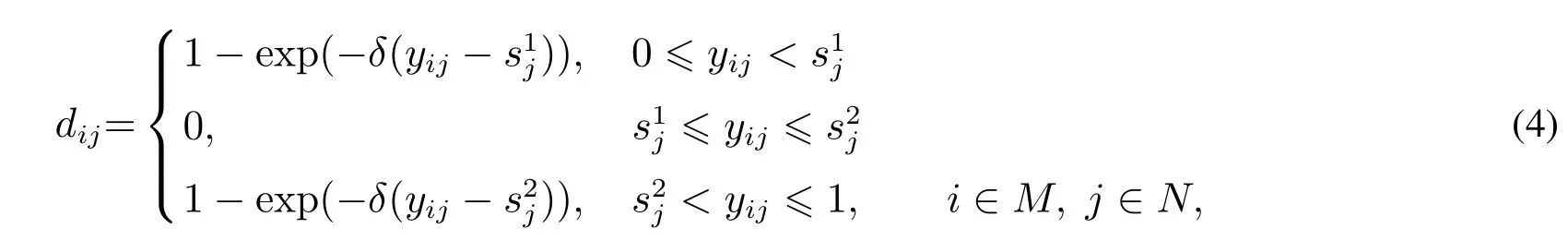
其中δ为决策者的后悔规避系数，δ＞0，δ越大，决策者的后悔规避程度越大.关于此类型的后悔-欣喜函数如图2所示.

图1 单基点Ⅰ型二元期望的后悔-欣喜函数Fig.1Regret-rejoice function of single pointⅠtype 2-tuple aspiration

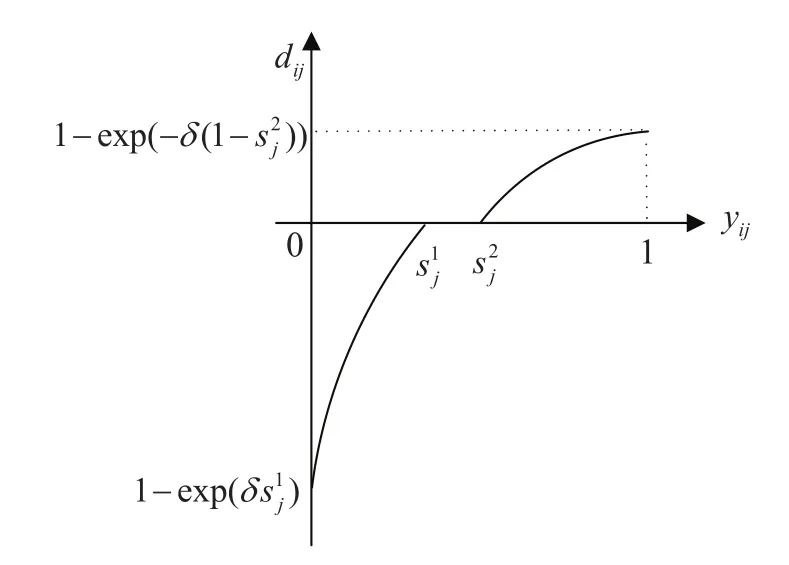
图2 双基点Ⅰ型二元期望的后悔-欣喜函数Fig.2Regret-rejoice function of double pointⅠtype 2-tuple aspiration

双基点Ⅰ型二元期望情形下，除了考虑决策者的后悔或欣喜值，还关注在期望概率和之间既没有欣喜也没有后悔的情形.特别地，当==sj时，双基点Ⅰ型二元期望的后悔-欣喜函数退化为单基点Ⅰ型二元期望情形的后悔-欣喜函数.可见，单基点Ⅰ型二元期望是双基点Ⅰ型二元期望的特例.

性质1关于双基点Ⅰ型二元期望，∀i∈M,∀j∈N，有1-exp（δ）≤dij≤1-exp（-δ（1-））≤1成立，并且若yij=0，则dij=1-exp（δ）；若yij=1，则dij=1-exp（-δ（1-））.特别地，如果== sj，双基点Ⅰ型二元期望退化为单基点Ⅰ型二元期望的情形，即有1-exp（δsj）≤dij≤1-exp（-δ（1-sj））≤1成立.并且若yij=0，则dij=1-exp（δsj）；若yij=1，则dij=1-exp（-δ（1-sj））.

对于双基点Ⅰ型二元期望的情形，如果yij-＜0，说明yij没有达到最低期望概率，称yij-为方案Ai关于期望概率的负偏差；如果yij-＞0，说明yij达到满意期望概率，称yij-为方案Ai关于期望概率的正偏差.对等量的正偏差和负偏差，若决策者是后悔规避的［19，20］，则决策者对关于负偏差的后悔程度比关于正偏差的欣喜程度更加敏感.

任取方案Ai和Ag，关于等量的正偏差和负偏差的后悔-欣喜值，有如下性质.

性质2对i,g∈M，j∈N，若存在yij＜和ygj＞满足|yij-|=|ygj-|，则有|dij|＞|dgj|成立.特别地，当==sj时，仍有|dij|＞|dgj|成立.

3）对于单基点Ⅱ型二元期望，若yij＞sj，则方案Ai“满足”目标价值tj的概率yij没有达到决策者关于属性Cj的期望概率，此时决策者选择方案Ai会感到后悔，反之，决策者会感到欣喜.因此，方案Ai关于二元期望（tj,sj）的后悔-欣喜值为

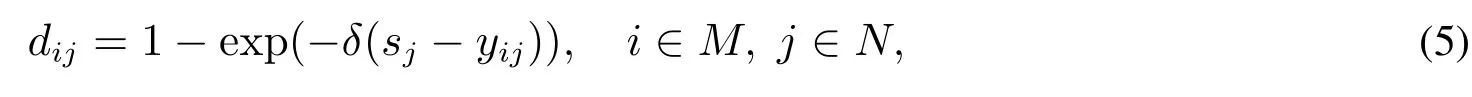
其中δ为决策者的后悔规避系数，δ＞0，δ越大，决策者的后悔规避程度越大.关于此类型的后悔-欣喜函数如图3所示.

4）对于双基点Ⅱ型二元期望，若yij＞，则方案Ai“满足”目标价值tj的概率yij没有达到决策者关于属性Cj的最低期望概率，此时决策者选择方案Ai会感到后悔；若yij＜，则yij达到决策者关于属性Cj的满意期望概率，此时决策者会感到欣喜；若≤yij≤，则yij达到决策者关于属性Cj的最低期望概率而没有达到满意期望概率，此时决策者既不会感到后悔也不会感到欣喜.因此，方案Ai关于二元期望（tj,sj）的后悔-欣喜值为

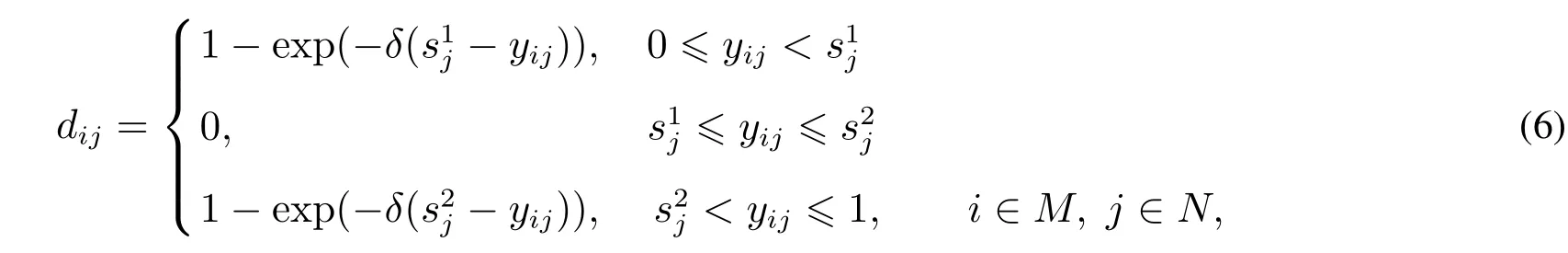
其中δ为决策者的后悔规避系数，δ＞0，δ越大，决策者的后悔规避程度越大.关于此类型的后悔-欣喜函数如图4所示.

性质3关于双基点Ⅱ型二元期望，∀i∈M，∀j∈N，有1-exp（δ（1-））≤dij≤1-exp（-δ）≤1成立.并且若yij=0，则dij=1-exp（-δ）；若yij=1，则dij=1-exp（δ（1-））.特别地，如果==sj，双基点Ⅱ型二元期望退化为单基点Ⅱ型二元期望的情形，即有1-exp（δ（1-sj））≤dij≤1-exp（-δsj）≤1成立.并且若yij=0，则dij=1-exp（-δsj）；若yij=1，则dij=1-exp（δ（1-sj））.

对于单基点Ⅱ型二元期望和双基点Ⅱ型二元期望，方案关于等量的正偏差和负偏差的后悔-欣喜值具有如下性质.

性质4对i,g∈M，j∈N，若存在yij＞和ygj＜满足|-yij|=|-ygj|，则有|dij|＞|dgj|成立.特别地，当==sj时，仍有|dij|＞|dgj|成立.

单基点Ⅰ型二元期望和双基点Ⅰ型二元期望是针对方案“满足”目标价值的概率越大越好的情形，因此后悔-欣喜值dij关于概率yij单调递增；单基点Ⅱ型二元期望和双基点Ⅱ型二元期望是针对方案“满足”目标价值的概率越小越好的情形，因此后悔-欣喜值dij关于概率yij单调递减.

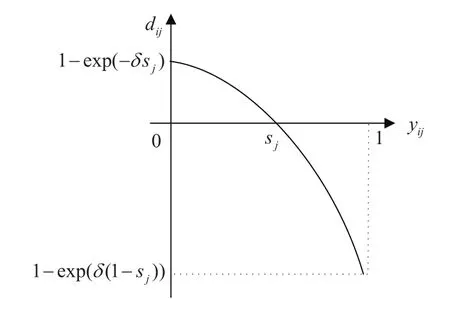
图3 单基点Ⅱ型二元期望的后悔-欣喜函数Fig.3Regret-rejoice function of singel pointⅡtype 2-tuple aspiration

图4 双基点Ⅱ型二元期望的后悔-欣喜函数Fig.4 Regret-rejoice function of double pointⅡtype 2-tuple aspiration

5）对于区间型二元期望，若yij＜或yij＞，则方案Ai“满足”目标价值tj的概率yij没有达到关于属性Cj的最低期望概率，此时决策者选择方案Ai会感到后悔；若s1j≤yij≤，则yij刚好达到关于属性Cj的最低期望概率，此时决策者选择方案Ai既不会产生后悔也不会产生欣喜.因此，方案Ai关于二元期望（tj,sj）的后悔-欣喜值为

其中δ为决策者的后悔规避系数，δ＞0，δ越大，决策者的后悔规避程度越大.

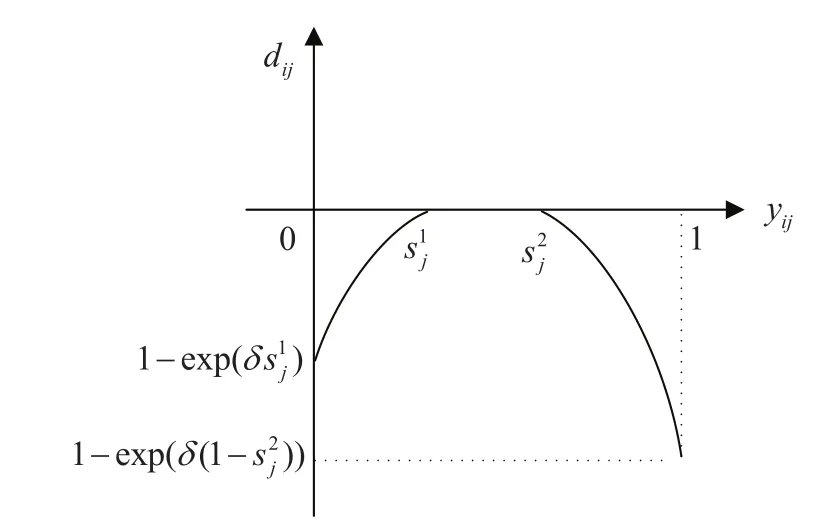
图5 区间型二元期望的后悔-欣喜函数（1）Fig.5Regret-rejoice function of interval type 2-tuple aspiration（1）

图6 区间型二元期望的后悔-欣喜函数（2）Fig.6Regret-rejoice function of interval type 2-tuple aspiration（2）

关于上述三种情形的区间型二元期望，方案的后悔-欣喜值具有如下性质.

性质5∀i∈M，∀j∈N，若yij=0，则dij=1-exp（）；若yij=1，则dij=1-exp（δ（1-））.

性质7∀i,g∈M，∀j∈N，如果存在yij≤和ygj≥，满足|yij-|=|-ygj|，则有|dij|= |dgj|成立.

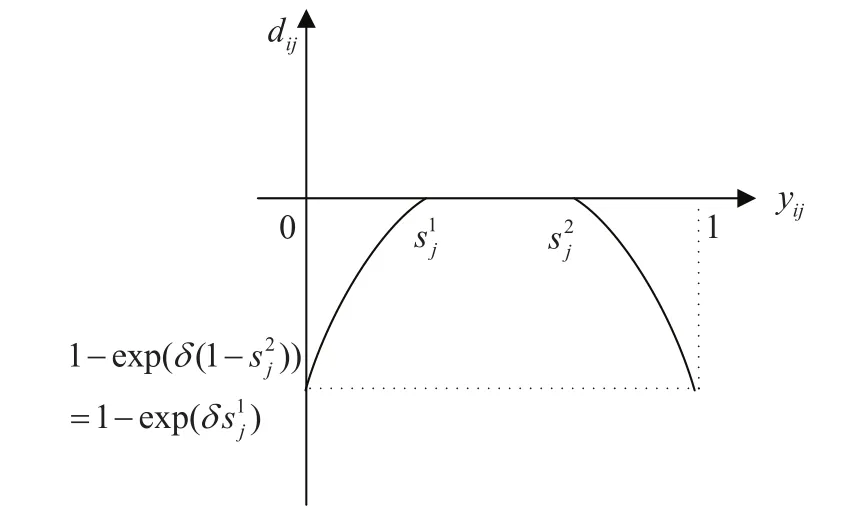
图7 区间型二元期望的后悔-欣喜函数（3）Fig.7Regret-rejoice function of interval type 2-tuple aspiration（3）

3.3 方案排序

根据方案Ai关于属性Cj的后悔-欣喜值dij和属性的权重wj，计算方案Ai的综合感知值为

根据综合感知值zi对方案进行排序，zi越大，相应的方案Ai越优.

综上所述，考虑决策者后悔规避行为情形下、具有二元期望的随机多属性决策方法的计算步骤如下：

步骤1根据式（1），式（2）计算方案Ai关于属性Cj的属性值xij“满足”目标价值tj的概率yij；

步骤2根据式（3）～式（7）计算方案Ai关于属性Cj的后悔-欣喜值dij；

步骤3根据式（8）计算方案Ai的综合感知值zi；

步骤4根据综合感知值zi对方案进行排序，zi越大，相应的方案Ai越优.

4 算例分析

考虑风险投资公司进行风险项目投资选择问题.某风险投资公司欲选择一个项目进行投资，现有五个备选的投资项目A1，A2，A3，A4和A5，投资决策者采用以下五个属性对五个备选项目进行评估和选择.投资成本C1（单位：万元）；预期收益C2（单位：万元）；风险损失值C3（单位：万元）；市场前景C4（单位：分）；绿色能源市场份额C5.其中C1和C3为成本型属性，C2，C4和C5为效益型属性.投资决策者通过聘请相关领域的专家对评价属性进行分析和评判，确定出五个评价属性的权重向量为W=（0.3,0.2,0.25,0.15,0.1）T.投资决策者根据投资项目的实际情况和相关历史数据进行统计分析和预测，针对属性C1，C2，C3和C5给出各投资项目的离散型或连续型随机属性值；并聘请十位相关专家对投资项目关于属性C4采用5分制进行打分，从而得到离散型随机决策信息.同时，投资决策者给出投资项目关于每个属性的二元期望，具体的随机决策信息和二元期望信息如表2和表3所示.

首先，根据式（1）和式（2），计算投资项目Ai关于属性Cj的属性值xij“满足”目标价值tj的概率yij，具体如表4所示.然后，根据式（3）～式（7），计算投资项目Ai关于二元期望Tj的后悔-欣喜值dij，具体如表5所示.这里取δ=0.3［21］.

进一步，根据式（8）计算投资项目Ai的综合感知值zi为

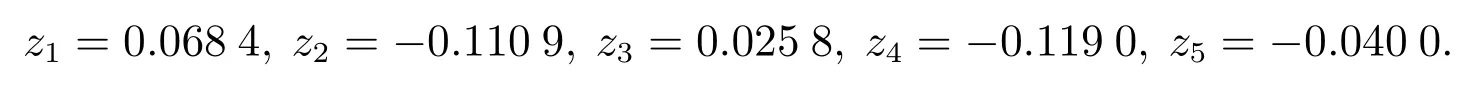
最后，根据zi对投资项目进行排序，得到排序结果为A1≻A3≻A5≻A2≻A4.因此，投资者选择投资项目A1最为合适.

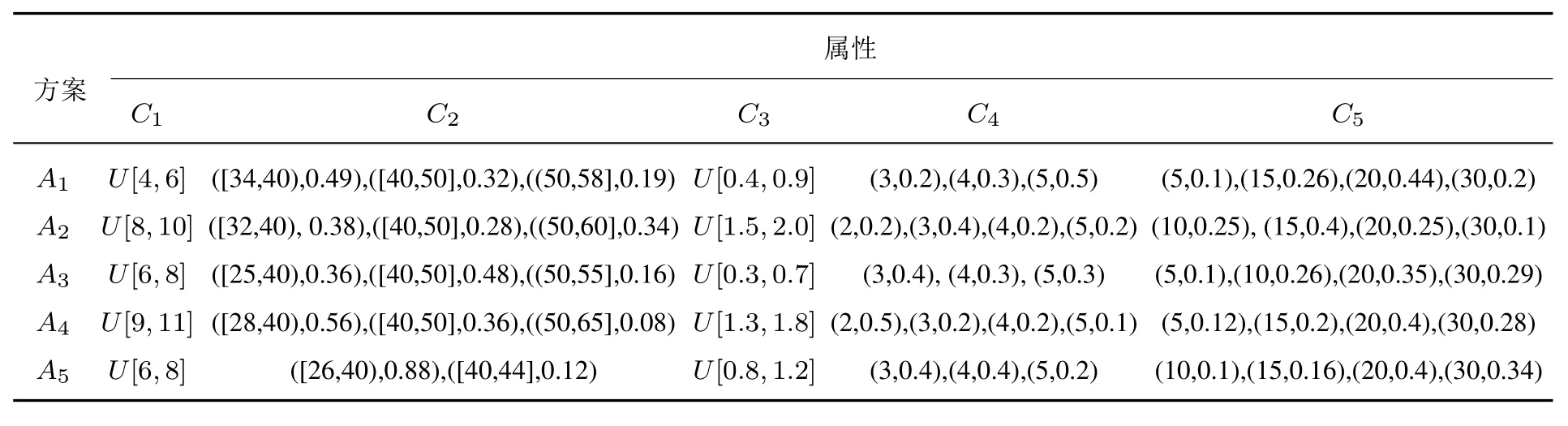
表2 决策矩阵X=［xij］5×5Table 2 Decision matrix X=［xij］5×5

表3 属性的二元期望Tj=（tj,sj）Table 32-tuple aspirations Tj=（tj,sj）of attributes

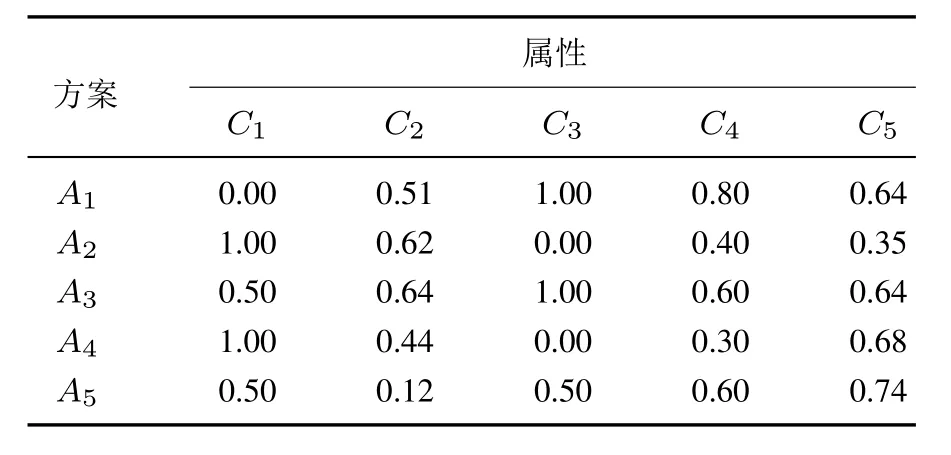
表4 方案“满足”目标价值tj的概率yijTable 4 The probabilities yijof alternatives meeting the target values tj

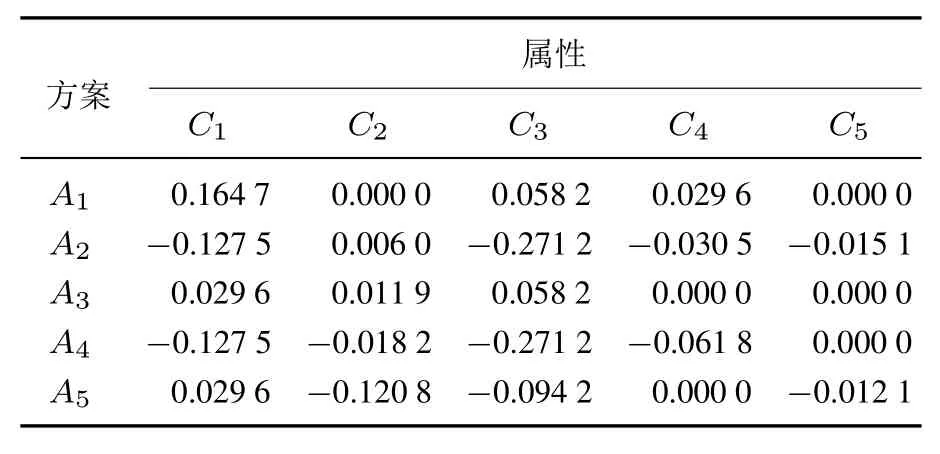
表5 方案的后悔-欣喜值dijTable 5Regret-rejoice values dijof alternaives

5 结束语

考虑决策者心理行为的随机决策方法研究具有重要的理论意义和实际应用价值.本文在考虑决策者后悔心理行为的情形下，针对属性具有二元期望信息的随机多属性决策问题，提出一种新的决策分析方法.该方法在备选方案排序过程中，首次提出了属性的二元期望信息形式，充分考虑了备选方案关于属性二元期望的满足程度.与已有研究相比，一方面，从理论上看，本文提出了关于属性二元期望的概念及其五种表达形式，弥补了以往随机多属性决策问题中属性期望形式单一的不足，可以更精确地表达决策者的偏好和意愿；另一方面，从实际应用上看，本文提出的方法考虑了决策者后悔规避的心理行为，弥补了以往研究中只考虑参照依赖和损失规避行为的不足，使决策结果更贴近现实，并且丰富了考虑决策者心理行为的随机多属性决策的解决方法与途径.在下一步的研究中，可以考虑决策者后悔行为的具有二元期望的多阶段随机多属性决策等问题.

［1］Zaras K.Rough approximation of a preference relation by a multi-attribute stochastic dominance for determinist and stochastic evaluation problems［J］.European Journal of Operational Research，2001，130（2）：305-314.

［2］Mousavi S M，Jolai F，Tavakkoli-Moghaddam R.A fuzzy stochastic multi-attribute group decision-making approach for selection problems［J］.Group Decision and Negotiation，2013，22（2）：207-233.

［3］梁海明，姜艳萍.考虑指标期望的产品外观设计方案的选择方法［J］.工业工程与管理，2014，19（1）：16-22.

Liang Haiming，Jiang Yanping.Selection on product appearance design alternative considering aspiration on criteria［J］.Industrial Engineering and Management，2014，19（1）：16-22.（in Chinese）

［4］Kahneman D，Tversky A.Prospect theory：An analysis of decision under risk［J］.Econometrica，1979，47（2）：263-291.

［5］邹高峰，张维，张海峰，等.中国市场条件下的前景理论资本资产定价模型［J］.系统工程学报，2013，28（3）：355-361.

Zou Gaofeng，Zhang Wei，Zhang Haifeng，et al.Prospect theory-based capital asset pricing model based on China security market［J］. Journal of Systems Engineering，2013，28（3）：355-361.（in Chinese）

［6］Hu J H，Yang L.Dynamic stochastic multi-criteria decision making method based on cumulative prospect theory and set pair analysis［J］.Systems Engineering Procedia，2011，2（1）：432-439.

［7］胡军华，杨柳.基于累积前景理论和随机加权法的随机多准则决策方法［J］.统计与决策，2012，21（1）：59-62.

Hu Junhua，Yang Liu.Stochastic multi-criteria decision-making method based on cumulative prospect theory and random weighting method［J］.Statistics and Decision，2012，21（1）：59-62.（in Chinese）

［8］王坚强，周玲.基于前景理论的灰色随机多准则决策方法［J］.系统工程理论与实践，2010，30（9）：1658-1664.

Wang Jianqiang，Zhou Ling.Grey-stochastic multi-criteria decision-making approach based on prospect theory［J］.Systems Engineering：Theory&Practice，2010，30（9）：1658-1664.（in Chinese）

［9］张洁，朱建军，刘思峰.基于前景理论的随机概率信息群集结模型研究［J］.中国管理科学，2011，19（1）：5-10.

Zhang Jie，Zhu Jianjun，Liu Sifeng.Research on coordinate information of prospect theory under the random information［J］.Chinese Journal of Management Science，2011，19（1）：5-10.（in Chinese）

［10］李鹏，吴军民，朱建军.基于新直觉模糊距离的随机决策方法［J］.系统工程理论与实践，2013，34（6）：1517-1524.

Li Peng，Wu Junmin，Zhu Jianjun.Stochastic multi-criteria decision-making methods based on new intuitionistic fuzzy distance［J］. Systems Engineering：Theory&Practice，2013，34（6）：1517-1524.（in Chinese）

［11］张晓，樊治平.基于前景理论的风险型混合多属性决策方法［J］.系统工程学报，2012，27（6）：772-780.

ZhangXiao，FanZhiping.Methodfor riskyhybridmultipleattributedecisionmakingbasedon prospecttheory［J］.JournalofSystems Engineering，2012，27（6）：772-780.（in Chinese）

［12］Tan C Q，Ip W H，Chen X H.Stochastic multiple criteria decision making with aspiration level based on prospect stochastic dominance［J］.Knowledge-Based Systems，2014，70（1）：231-241.

［13］张晓，樊治平.一种基于前景随机占优准则的随机多属性决策方法［J］.控制与决策，2010，25（12）：1875-1879.

Zhang Xiao，Fan Zhiping.Method for stochastic multiple attribute decision making based on prospect stochastic dominance rule［J］. Control and Decision，2010，25（12）：1875-1879.（in Chinese）

［14］Zeelenberg M.Anticipated regret，expect feedback，and behavioral decision making［J］.Journal of Behavioral Decision Making，1999，12（2）：93-106.

［15］Zeelenberg M，Pieters R.Beyond valence in customer dissatisfaction：A review and new finding on behavioral responses to regret and disappointment in fail services［J］.Journal of Business Research，2004，57（4）：445-455.

［16］Kujawski E.A reference-dependent regret model for deterministic tradeoff studies［J］.System Engineering，2005，8（2）：119-137.

［17］Klubeck M.Metrics：How to Improve Key Business Results［M］.NewYork：Apress，2011.

［18］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，2001.

Sheng Zhou，Xie Shiqian，Pan Chengyi.Probability and Mathematical Statistics［M］.Beijing：Higher Education Press，2001.（in Chinese）

［19］Bell D E.Regret in decision making under uncertainty［J］.Operations Research，1982，30（5）：961-981.

［20］Chorus C G.Regret theory-based route choices and traffic equilibria［J］.Transportmetrica，2012，8（4）：291-305.

［21］张晓，樊治平，陈发动.考虑后悔规避的风险型多属性决策方法［J］.系统管理学报，2014，23（1）：111-117.

Zhang Xiao，Fan Zhiping，Chen Fadong.Risk multiple attribute decision making with regret aversion［J］.Journal of Systems& Management，2014，23（1）：111-117.（in Chinese）

Method of stochastic multi-attribute decision making with 2-tuple aspirations considering regret behavior

Liang Xia，Jiang Yanping

With respect to the stochastic multi-attribute decision making problem with 2-tuple aspirations on attributes，considering the regret behavior of the decision makers，a decision method is proposed.According to the stochastic decision information and the 2-tuple aspirations on attributes，the probabilities of evaluations meeting the target values are calculated.Then，considering the regret behavior of the decision maker，and based on the aspiration probabilities in the 2-tuple aspirations，the regret-rejoice values of the alternatives on each attribute are calculated.Further，the overall perceived values of the alternatives are computed according to the regret-rejoice values.Finally，an example of venture investment is given to illustrate the feasibility and practicability of the proposed method.

stochastic multi-attribute decision making；2-tuple aspiration；regret behavior；ranking

C934

A

1000-5781（2015）06-0719-09

10.13383/j.cnki.jse.2015.06.001

梁霞（1986-），女，山东济南人，博士生，研究方向：管理决策分析，Email：susanliangxia@163.com；

2014-09-06；

2015-01-22.

国家自然科学基金资助项目（71271050；71571040）；高等学校博士学科点专项科研基金资助项目（201100421100-11）.

姜艳萍（1968-），女，辽宁沈阳人，博士，教授，研究方向：管理决策分析，Email：ypjiang@mail.neu.edu.cn.